六年级数学下册教案数的认识人教版(3课时)
文档属性
| 名称 | 六年级数学下册教案数的认识人教版(3课时) |

|
|
| 格式 | doc | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
第一部分 数与代数
1 数的认识
第1课时 数的认识(1)
课时目标导航
教学导航
一、复习内容
数的认识(1)。(教材第72页、第73页第1~2题)
二、复习目标
1.使学生比较系统地掌握有关自然数、整数、分数、小数、百分数和负数的基础知识,进一步明确这些概念间的联系与区别。
2.经历有关知识的归纳与整理的过程,体验归纳整理和概括的学习方法。
3.感受数学在日常生活中的广泛应用,体验学习成功的快乐,树立学习的信心。
三、重点难点
重点:自然数、整数、分数、小数、百分数、负数的意义的整理与归纳,以及在直线上表示数。
难点:整理、复习与练习的有机结合。
教学过程
一、引导回顾
教师引导:小学阶段的数学知识我们已经学完了,从今天开始我们一起来整理和复习所学过的知识,我们先来复习有关数的知识,请同学们回忆一下,我们在小学阶段都学过哪几种数?
学生各自回忆,同桌互相讨论。
点名学生说一说小学阶段学过哪几种数。
教师在恰当的位置板书:自然数、整数、分数、小数、百分数、负数。
然后让学生尝试把学过的数整理成图表示出来,教师巡视学生的表示方法。
二、回顾整理
【回顾1】数的分类。
数
或
数
【回顾2】自然数、整数、分数、小数、百分数和负数的意义。
自然数:用来表示物体个数的0、1、2、3、4……这样的数叫做自然数。一个物体也没有就用0表示。
整数:像-3、-2、-1、0、1、2、3……这样的数统称为整数。
整数
分数:把单位“1”平均分成若干份,表示这样一份或几份的数叫做分数,如。其中表示一份的数是这个分数的分数单位,如的分数单位是。
分数与除法的关系:a÷b=(b≠0)。
分数
小数:像3.45、0.85、2.60、36.6、1.2……这样的数叫做小数。
小数
百分数:表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分比或百分率。
负数:像-7、-4.3、-0.5……这样的数叫做负数,所有的负数都小于0。
【回顾3】在直线上表示数。
画一条直线,在直线上取一点,表示0。0点向右为正数所在的位置,0点向左为负数所在的位置。
【回顾4】分数、小数、百分数的互化。
【回顾5】分数、小数的基本性质。
分数的基本性质 分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变
小数的基本性质 在小数的末尾添上0或者去掉0,小数的大小不变
小数的基本性质与分数的基本性质的关系 小数的基本性质是分数的基本性质的特殊情况
三、知识应用
教学教材第73页“做一做”。
学生先分组说一说,然后教师指名三位学生分别举例说一说这三个数的含义。
答案略,可根据实际情况举例。
四、巩固反馈
1.把下面这些数根据各自分类填入下面的括号中。(学生独立完成,同桌之间相互订正)
12,75%,300,-4.8,1,6.7575,,3.333,0,,π,3256,5.5%,-4。
自然数:{12,300,1,0,3256};
整数:{12,300,1,0,3256,-4};
负数:{-4.8,-4};
分数:;
小数:{-4.8,6.7575,3.333,π};
百分数:{75%,5.5%}。
2.判断。(点名学生回答,给出判断结果及理由)
(1)自然数都是整数,整数都是自然数。(?)
(2)假分数大于1。(?)
(3)带分数都比假分数大。(?)
(4)百分数一定大于1。(?)
五、课堂小结
请同学们把数的认识的相关知识归纳整理一下,并在小组内互相讨论交流。
板书设计
数的认识(1)
自然数、整数、分数、小数、百分数、负数。
整数
分数与除法的关系:a÷b=(b≠0)。
分数
小数
教学反思
1.我们知道,复习课的本质就是查漏补缺、系统整理和综合应用。本节课我在新课程理念的指导下,灵活整理知识点,学生在我的引领下积极地完成了复习内容。
数的认识中有很多知识点都要求学生理解它们的区别和联系,本节课中,就涉及整数、分数、小数方面的一系列知识,比如:数的分类、整数的分类、分数的意义、小数的意义以及这些知识之间一系列的联系与区别等,如整数、小数、真分数、假分数、带分数之间的关系及改写等,学生非常容易混淆。
在处理知识梳理方面,我先在前一天让学生自己回家复习本部分知识,并用自己的方式写下整理图。在本节课上我提出问题后让学生展示各自的整理图,然后让学生自己汇报梳理知识点,进而我加以补充、板书,很好地处理“补”与“梳”的关系,使学生对于本节课所要复习的内容一目了然,这一做法同时也起到摸清学生底子的作用。这是本次复习课比较成功的一方面,但在配套练习中仍存在不足,没有很好地将练习题与整理复习的内容有效地结合起来,“理”与“练”没有达到双丰收的效果。
在以后的复习教学当中,我会提前告诉学生下节课要复习的知识点具体有哪些,还要让学生自己整理,学生整理的过程也是复习回顾知识的过程。练习时,要有基础的练习和提高的练习。课堂上首先是对知识点进行回顾后马上进行独立自主的练习,最后,对多数学生有问题的地方再进行重点复习。同时,在教学当中,要加强对学生思维的拓展,培养学生学习数学的兴趣,提高他们分析问题和解决问题的能力。
2.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
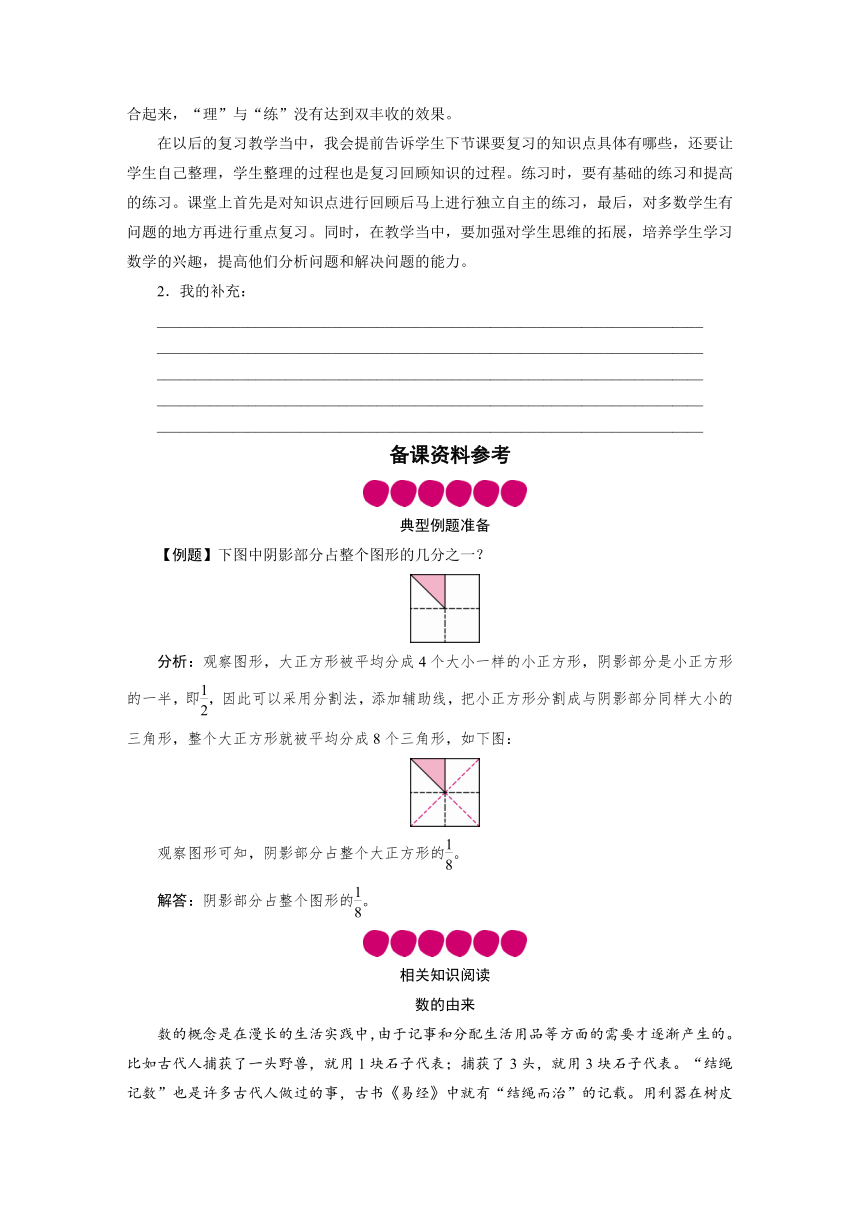
【例题】下图中阴影部分占整个图形的几分之一?
分析:观察图形,大正方形被平均分成4个大小一样的小正方形,阴影部分是小正方形的一半,即,因此可以采用分割法,添加辅助线,把小正方形分割成与阴影部分同样大小的三角形,整个大正方形就被平均分成8个三角形,如下图:
观察图形可知,阴影部分占整个大正方形的。
解答:阴影部分占整个图形的。
相关知识阅读
数的由来
数的概念是在漫长的生活实践中,由于记事和分配生活用品等方面的需要才逐渐产生的。比如古代人捕获了一头野兽,就用1块石子代表;捕获了3头,就用3块石子代表。“结绳记数”也是许多古代人做过的事,古书《易经》中就有“结绳而治”的记载。用利器在树皮或兽皮上刻痕,或用小棍摆在地上计数也是古人常用的办法。这些办法用得多了,就逐渐形成了数的概念和记数的符号。
我国古代很重视记数符号,最古老的甲骨文和钟鼎中都有记数的符号,不过难写难认。后来我们的祖先创造了一种十分重要的计数方法——筹算。筹算以算筹记数、运算,算筹用的是竹制的小棍,也有骨制的,按规定的横竖长短顺序摆好,算筹的摆法也就成了记数的符号。但算筹数码中没有“零”,遇到“零”就空位,后来有人把铜钱摆在空位上,以免弄错。公元6世纪的印度人最早用黑点(·)表示零,后来逐渐演变成了“0”。
现在我们用的1、2、3、4、5、6、7、8、9、0,人们称之为阿拉伯数字。这些数字原来是由古印度人发明的,后来传到阿拉伯,又经阿拉伯传到欧洲,欧洲人误以为是阿拉伯人发明的,就把它们叫做阿拉伯数字。因为流传了许多年,人们叫得顺口,所以人们将错就错,把这些古印度人发明的数字符号叫做阿拉伯数字。现在,阿拉伯数字已成了全世界通用的数字。
第2课时 数的认识(2)
课时目标导航
教学导航
一、复习内容
数的认识(2)。(教材第73页第3~6题)
二、复习目标
1.使学生掌握十进制计数法和整数、小数的数位顺序以及计数单位。
2.使学生能比较熟练地进行数的大小比较。
3.通过复习,使学生能进一步理解因数、倍数、质数、合数等含义。
4.进一步理解和掌握分数和小数的基本性质。
三、重点难点
重点:理解和重温相关概念的含义。
难点:掌握因数和倍数的相关知识。
教学过程
一、回顾整理
【回顾1】十进制计数法。
整数和小数都是按十进制计数法写出的数,其中个、十、百、千……以及十分之一、百分之一……都是计数单位。各个计数单位所占的位置,叫做数位。数位是按一定顺序排列的。
【回顾2】因数与倍数。
(1)如果a÷b=c(a、b、c均为整数,且b≠0),那么说明a是b的倍数,b是a的因数。
注意:倍数与因数是相互依存的。只能说谁是谁的倍数,谁是谁的因数,而不能单独说某个数是倍数,也不能单独说某个数是因数。
(2)在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
(3)一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数);一个数,如果除了1和它本身还有其他的因数,这样的数叫做合数。
注意:①1既不是合数,也不是质数。
②最小的质数是2,没有最大的质数。
③最小的合数是4,没有最大的质数。
(4)几个数公有的因数,叫做这几个数的公因数,其中最大的一个数叫做这几个数的最大公因数;几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个数叫做这几个数的最小公倍数。
【回顾3】小数点位置移动的规律。
(1)小数点向右移动一位,小数就扩大到原来的10倍;小数点向右移动两位,小数就扩大到原来的100倍……
(2)小数点向左移动一位,小数就缩小到原来的;小数点向左移动两位,小数就缩小到原来的……
【回顾4】正数的大小比较。
正数的大小比较
二、知识应用
1.按要求排序。(学生独立完成,教师点名学生板演,集体订正)
(1)将、、按从大到小的顺序排列起来。
>>
(2)将5.2、5.、5.211按从小到大的顺序排列起来。
5.211<5.2<5.
2.填空。(学生独立完成,教师点名学生回答,集体订正)
(1)把的分母缩小到原来的,要使分数的大小不变,分子应该(缩小到原来的),分数变成( )。
(2)当分数的分子加上4时,为了使分数的大小不变,分母要加上( 18 )。
(3)60的所有因数有(1、2、3、4、5、6、10、12、15、20、30、60),其中质数有( 2、3、5 )。
三、巩固反馈
1.75和15的最大公因数是( 15 ),最小公倍数是( 75 )。
2.判断快车。(点名学生回答,给出判断结果及理由)
(1)若x÷y=2020(x、y是自然数,y≠0),则x是2020的倍数。(?)
(2)最小的奇数是1,最小的偶数是2。(?)
3.在里填上“>”或“<”。(学生齐答,集体订正)
1249<1250
3.11>31.1%
9.08>8.19
>
62830400<628030400
四、课堂小结
通过今天的学习,你掌握了什么?
板书设计
数的认识(2)
教学反思
1.经历知识整理过程。
在课堂上,应该让学生经历知识的整理过程,让学生掌握整理的方法。可以要求学生亲自参与知识的整理过程,这样不但加深了学生对知识的理解,还能从中掌握复习知识的方法,这样有利于学生对知识的复习。
2.辨清各个概念,揭示概念本质属性。
本节课中的概念较多且容易混淆,比如数位、位数与计数单位,偶数与奇数,因数与倍数,因数与公因数,倍数与公倍数,质数与合数等,教学中多次采用比较的形式,让学生在比较的过程中辨清知识的相同点和不同点,帮助学生形成清晰的概念。我在教学中要求学生对一些重点词和一些重点符号要高度关注,比如:关注省略号的作用,让学生思考省略了什么,通过思考揭示概念的本质属性。
3.突出板书在整理知识中的作用。
在教学中关注板书在整理知识中的作用,多次利用板书来呈现知识的相互联系,使学生可以从板书中理解知识的联系与区别,帮助学生形成清晰的概念。板书还可以给学生提供一个复习提纲,学生可以按照板书的内容组织复习,突出重点,层次清楚,容易达到一个较好的复习效果。
4.加强学生对基本概念的理解与记忆。
只有熟练掌握基础知识和相关概念,学生才能很好地进行判断、分析,才能真正理解并掌握知识及知识间的内在联系与区别。
5.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】要使<<成立,a可以是哪些整数?
分析:7、14、4的最小公倍数是28。把这三个分数通分化成分子是28的分数,即<<。由于分子相同的分数分母大的反而小,则可以得出119<2a<128,各项都除以2就是59.5<a<64,因为a是整数,故a可以是60、61、62、63。
解答:a可以是60、61、62、63。
解法归纳:解答本题的关键是把这几个分数通分化成分子相同的分数,同分子的分数比较大小,分母大的分数反而小。
相关知识阅读
点错的小数点
学习数学不仅解题思路要正确,具体解题过程也不能出错,差之毫厘,往往失之千里。
美国芝加哥一个靠养老金生活的老太太,在医院进行了一次小手术。两星期后,她接到医院寄来的一张账单,款数是63440美元。她看到偌大的数字,不禁大惊失色,导致心脏病突发,倒地身亡。后来,有人向医院一核对,原来是把小数点的位置放错了,实际上只需要付63.44美元。
点错一个小数点,竟要了一条人命。正如牛顿所说:“在数学中,最微小的误差也不能忽略。”
第3课时 数的认识(练习课)
课时目标导航
教学导航
一、教学内容
数的认识的运用练习。(教材第74~75页练习十四第1~6题)
二、教学目标
1.使学生进一步理解和掌握整数、分数、小数、百分数的意义和性质。
2.使学生进一步理解因数、倍数、质数、合数等的意义,能熟练地找出两个数的公因数、公倍数等。
3.熟练掌握2、3、5的倍数的特征,并能正确地解决有关问题。
三、重点难点
重点:巩固整数、分数、小数、百分数的基本性质和概念,学会简单的运用。
难点:了解因数、倍数、合数的概念及其综合运用,从练习中找出2、3、5这三个基本数字的倍数的特征,进行归纳小结。
教学过程
一、基础练习
填一填。(课件出示)
(1)一个数是30的因数,又是2和5的倍数,这个数是( )。
(2)一个数是36的因数,也是2和3的倍数,而且比15小,这个数是( )。
(3)根据25×4=100,可知( )是( )的因数,( )也是( )的因数;( )是( )的倍数,也是( )的倍数。
教师指出:已知a、b、c均为正整数(为了方便,在研究因数和倍数时,所指的数不包括0),且a×b=c,那么c就是a和b的倍数,a和b就是c的因数。倍数和因数是相互依存的。
二、指导练习
1.教学教材第74页练习十四第1题。
本题主要考查学生的记数能力,数字和文字相互转化的综合运用能力。将小数49.7 ℃和零下52.3 ℃用数字进行记录,这考查了正数、负数的记法。(2)(3)小题分别考查因数、倍数的相关概念,“打折”的相关运用。注意记数时,正数前面的“+”可以省略不写出,而负数前面的“-”必须写出来。
教师强调:“打七折”表示现价为原价的70%;因数、倍数均是针对非0的自然数而言的。
2.教学教材第74页练习十四第2题。
本题考查将末尾有多个0的数改写成用“万”或“亿”等作计数单位的数,使得书写更加简单、便捷,比如:中国人口有13.4141亿人。同时必须掌握保留小数位数的方法。
教师强调:亿后面是8个0,当不够时就需要小数点继续左移,处理小数问题;万后面是4个0,其他类推。保留小数一般按照“四舍五入”法进行取舍。
学生独立完成,集体订正。
3.教学教材第74页练习十四第3题。
(1)说出数字含义,题目中2在十位、百分位、分子、百位等不同位置,2的含义就是2所代表数位的含义。因此本题需要同学们熟悉分数、小数、整数的组成,理解数位的含义。
(2)本题属于简单分析题,学生独立完成,集体交流,相互订正。
4.教学教材第75页练习十四第4题。
本题主要考查分数、小数、百分数的相互转化问题。比如:将0.4写成分数为,写成百分数为40%,其余题依此类推。
教师强调:三种数之间的相互转化可以有效地简化综合运用中的计算问题。
5.教学教材第75页练习十四第5题。
(1)考查奇数、偶数、合数、质数、倍数、因数、公因数和公倍数的相关概念,解题前可要求学生进行概念的复述,以便更好地解答此题。
(2)考查了排列的相关知识点,2、3、4、5组成没有重复数字的两位数可以是12种,依次为23、24、25、32、34、35、42、43、45、52、53、54。
(3)根据题目中的要求找出质数、合数、偶数、奇数、倍数和公倍数进行分析解答。
(4)教师强调:分步骤有序地进行解答,并且确保又快又准。
6.教学教材第75页练习十四第6题。
本题是对数的相关概念和性质的辨析题。先组织学生独立思考,然后同桌间互相交流答案,并指出错误的原因是什么,集体订正。
三、巩固练习
1.完成教材第75页“练习十四”第7题。(学生独立完成,集体订正)
(1)0.99999 1 (2) 0
2.完成教材第75页“练习十四”第8题。(学生先独立思考,再小组内交流讨论,教师点名学生回答)
<<<
发现规律:分母与分子的差相等的真分数相比较,分母越大,这个分数就越大。
>
验证:=,=,因为>,所以>。
3.完成教材第75页“练习十四”第9*题。(学生先独立思考,再小组内交流讨论,教师适时提醒:本题需要转换思维,对问题进行转化,运用表内乘法或公倍数的知识解决问题,可不用设未知数列方程解答)
8和10的最小公倍数是40,40+6=46(个),因为40<46<50,所以这箱苹果有46个。
四、课堂小结
你能说一说因数和公因数、倍数和公倍数有什么联系和区别吗?在我们生活中有哪些运用?
板书设计
数的认识(练习课)
第1题:(1)49.7 -52.3 (2)b a (3)70 30
第2题:(1)13.4 12.2 (2)1707.5 937.3
第3题:2个十 2个百分之一 2个 2个百
第4题: 40% 0.75 75% 0.8
第5题:12个 (1)23、25、35、43、45、53是奇数;24、32、34、42、52、54是偶数。
(2)23、43、53是质数;24、25、32、34、35、42、45、52、54是合数。
(3)32、42、52、24、34、54是2的倍数;24、42、45、54是3的倍数;25、35、45是5的倍数。
(4)24、42、54 45
第6题:(1)? (2)? (3)? (4)? (5)?
教学反思
1.本节课是练习课,是针对数的认识的系统练习。
在整体的练习中我发挥了学生的主体作用,让他们担任解决问题的主角。另外一方面我强调循序渐进的复习模式,让学生在练习中体会和巩固这些数的意义和性质。但是学生作业中的问题特别多:(1)质数和合数分辨不清,51和91被许多学生当成质数;(2)写50以内的质数,错得太多,不是多写就是少写;(3)与奇数、偶数混合后的判断题出错多。为此要让学生深刻理解质数、合数、奇数、偶数各自的概念,掌握各自的判断方法,也要让学生背一背质数表,帮助学生快速辨别质数,还要告诫学生要细心,要有耐心和学好数学的信心。应再额外教给学生判断质数的简便有效方法:依次用2,3,5,7,11等质数去除这个数,看有没有余数,如91除以7等于13,121除以11等于11。
在分数、小数、百分数等简单的数的改写及转化中,学生掌握得还是非常熟练的,值得肯定。
2.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】甲、乙、丙三人打靶,每人打三枪,三人各自中靶的环数之积都是60,按个人中靶的总环数由高到低排,依次是甲、乙、丙。他们中有一人打中4环,打中4环的那一枪是谁打的?(环数是不超过10的自然数)
分析:60的因数有1、2、3、4、5、6、10、12、15、20、30、60,其中小于等于10的3个因数的积为60的有60=1×6×10,60=2×3×10,60=2×5×6,60=4×3×5。
每一种情况打中的环数分别为1+6+10=17(环),2+3+10=15(环),2+5+6=13(环),4+3+5=12(环)。
按中靶数的高低排列为17、15、13、12。
由于甲、乙、丙三人按个人中靶的总环数由高到低排列,依次是甲、乙、丙,且有一人打中4环,所以靶子上打中4环的那一枪只能是丙打的。
解答:60=1×6×10=2×3×10=2×5×6=4×3×5
在这4种情况中,总环数分别为17、15、13、12。由于三个人按个人中靶的总环数由高到低排列依次是甲、乙、丙,且有一人打中4环,所以靶子上打中4环的那一枪是丙打的。
答:打中4环的那一枪是丙打的。
解法归纳:找到乘积是60(因数是不超过10的自然数)的所有情况,从而找出每个人的打靶环数的可能情况,再根据三个人按个人中靶的总环数由高到低排列依次是甲、乙、丙确定情况。
1 数的认识
第1课时 数的认识(1)
课时目标导航
教学导航
一、复习内容
数的认识(1)。(教材第72页、第73页第1~2题)
二、复习目标
1.使学生比较系统地掌握有关自然数、整数、分数、小数、百分数和负数的基础知识,进一步明确这些概念间的联系与区别。
2.经历有关知识的归纳与整理的过程,体验归纳整理和概括的学习方法。
3.感受数学在日常生活中的广泛应用,体验学习成功的快乐,树立学习的信心。
三、重点难点
重点:自然数、整数、分数、小数、百分数、负数的意义的整理与归纳,以及在直线上表示数。
难点:整理、复习与练习的有机结合。
教学过程
一、引导回顾
教师引导:小学阶段的数学知识我们已经学完了,从今天开始我们一起来整理和复习所学过的知识,我们先来复习有关数的知识,请同学们回忆一下,我们在小学阶段都学过哪几种数?
学生各自回忆,同桌互相讨论。
点名学生说一说小学阶段学过哪几种数。
教师在恰当的位置板书:自然数、整数、分数、小数、百分数、负数。
然后让学生尝试把学过的数整理成图表示出来,教师巡视学生的表示方法。
二、回顾整理
【回顾1】数的分类。
数
或
数
【回顾2】自然数、整数、分数、小数、百分数和负数的意义。
自然数:用来表示物体个数的0、1、2、3、4……这样的数叫做自然数。一个物体也没有就用0表示。
整数:像-3、-2、-1、0、1、2、3……这样的数统称为整数。
整数
分数:把单位“1”平均分成若干份,表示这样一份或几份的数叫做分数,如。其中表示一份的数是这个分数的分数单位,如的分数单位是。
分数与除法的关系:a÷b=(b≠0)。
分数
小数:像3.45、0.85、2.60、36.6、1.2……这样的数叫做小数。
小数
百分数:表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分比或百分率。
负数:像-7、-4.3、-0.5……这样的数叫做负数,所有的负数都小于0。
【回顾3】在直线上表示数。
画一条直线,在直线上取一点,表示0。0点向右为正数所在的位置,0点向左为负数所在的位置。
【回顾4】分数、小数、百分数的互化。
【回顾5】分数、小数的基本性质。
分数的基本性质 分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变
小数的基本性质 在小数的末尾添上0或者去掉0,小数的大小不变
小数的基本性质与分数的基本性质的关系 小数的基本性质是分数的基本性质的特殊情况
三、知识应用
教学教材第73页“做一做”。
学生先分组说一说,然后教师指名三位学生分别举例说一说这三个数的含义。
答案略,可根据实际情况举例。
四、巩固反馈
1.把下面这些数根据各自分类填入下面的括号中。(学生独立完成,同桌之间相互订正)
12,75%,300,-4.8,1,6.7575,,3.333,0,,π,3256,5.5%,-4。
自然数:{12,300,1,0,3256};
整数:{12,300,1,0,3256,-4};
负数:{-4.8,-4};
分数:;
小数:{-4.8,6.7575,3.333,π};
百分数:{75%,5.5%}。
2.判断。(点名学生回答,给出判断结果及理由)
(1)自然数都是整数,整数都是自然数。(?)
(2)假分数大于1。(?)
(3)带分数都比假分数大。(?)
(4)百分数一定大于1。(?)
五、课堂小结
请同学们把数的认识的相关知识归纳整理一下,并在小组内互相讨论交流。
板书设计
数的认识(1)
自然数、整数、分数、小数、百分数、负数。
整数
分数与除法的关系:a÷b=(b≠0)。
分数
小数
教学反思
1.我们知道,复习课的本质就是查漏补缺、系统整理和综合应用。本节课我在新课程理念的指导下,灵活整理知识点,学生在我的引领下积极地完成了复习内容。
数的认识中有很多知识点都要求学生理解它们的区别和联系,本节课中,就涉及整数、分数、小数方面的一系列知识,比如:数的分类、整数的分类、分数的意义、小数的意义以及这些知识之间一系列的联系与区别等,如整数、小数、真分数、假分数、带分数之间的关系及改写等,学生非常容易混淆。
在处理知识梳理方面,我先在前一天让学生自己回家复习本部分知识,并用自己的方式写下整理图。在本节课上我提出问题后让学生展示各自的整理图,然后让学生自己汇报梳理知识点,进而我加以补充、板书,很好地处理“补”与“梳”的关系,使学生对于本节课所要复习的内容一目了然,这一做法同时也起到摸清学生底子的作用。这是本次复习课比较成功的一方面,但在配套练习中仍存在不足,没有很好地将练习题与整理复习的内容有效地结合起来,“理”与“练”没有达到双丰收的效果。
在以后的复习教学当中,我会提前告诉学生下节课要复习的知识点具体有哪些,还要让学生自己整理,学生整理的过程也是复习回顾知识的过程。练习时,要有基础的练习和提高的练习。课堂上首先是对知识点进行回顾后马上进行独立自主的练习,最后,对多数学生有问题的地方再进行重点复习。同时,在教学当中,要加强对学生思维的拓展,培养学生学习数学的兴趣,提高他们分析问题和解决问题的能力。
2.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】下图中阴影部分占整个图形的几分之一?
分析:观察图形,大正方形被平均分成4个大小一样的小正方形,阴影部分是小正方形的一半,即,因此可以采用分割法,添加辅助线,把小正方形分割成与阴影部分同样大小的三角形,整个大正方形就被平均分成8个三角形,如下图:
观察图形可知,阴影部分占整个大正方形的。
解答:阴影部分占整个图形的。
相关知识阅读
数的由来
数的概念是在漫长的生活实践中,由于记事和分配生活用品等方面的需要才逐渐产生的。比如古代人捕获了一头野兽,就用1块石子代表;捕获了3头,就用3块石子代表。“结绳记数”也是许多古代人做过的事,古书《易经》中就有“结绳而治”的记载。用利器在树皮或兽皮上刻痕,或用小棍摆在地上计数也是古人常用的办法。这些办法用得多了,就逐渐形成了数的概念和记数的符号。
我国古代很重视记数符号,最古老的甲骨文和钟鼎中都有记数的符号,不过难写难认。后来我们的祖先创造了一种十分重要的计数方法——筹算。筹算以算筹记数、运算,算筹用的是竹制的小棍,也有骨制的,按规定的横竖长短顺序摆好,算筹的摆法也就成了记数的符号。但算筹数码中没有“零”,遇到“零”就空位,后来有人把铜钱摆在空位上,以免弄错。公元6世纪的印度人最早用黑点(·)表示零,后来逐渐演变成了“0”。
现在我们用的1、2、3、4、5、6、7、8、9、0,人们称之为阿拉伯数字。这些数字原来是由古印度人发明的,后来传到阿拉伯,又经阿拉伯传到欧洲,欧洲人误以为是阿拉伯人发明的,就把它们叫做阿拉伯数字。因为流传了许多年,人们叫得顺口,所以人们将错就错,把这些古印度人发明的数字符号叫做阿拉伯数字。现在,阿拉伯数字已成了全世界通用的数字。
第2课时 数的认识(2)
课时目标导航
教学导航
一、复习内容
数的认识(2)。(教材第73页第3~6题)
二、复习目标
1.使学生掌握十进制计数法和整数、小数的数位顺序以及计数单位。
2.使学生能比较熟练地进行数的大小比较。
3.通过复习,使学生能进一步理解因数、倍数、质数、合数等含义。
4.进一步理解和掌握分数和小数的基本性质。
三、重点难点
重点:理解和重温相关概念的含义。
难点:掌握因数和倍数的相关知识。
教学过程
一、回顾整理
【回顾1】十进制计数法。
整数和小数都是按十进制计数法写出的数,其中个、十、百、千……以及十分之一、百分之一……都是计数单位。各个计数单位所占的位置,叫做数位。数位是按一定顺序排列的。
【回顾2】因数与倍数。
(1)如果a÷b=c(a、b、c均为整数,且b≠0),那么说明a是b的倍数,b是a的因数。
注意:倍数与因数是相互依存的。只能说谁是谁的倍数,谁是谁的因数,而不能单独说某个数是倍数,也不能单独说某个数是因数。
(2)在自然数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
(3)一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数);一个数,如果除了1和它本身还有其他的因数,这样的数叫做合数。
注意:①1既不是合数,也不是质数。
②最小的质数是2,没有最大的质数。
③最小的合数是4,没有最大的质数。
(4)几个数公有的因数,叫做这几个数的公因数,其中最大的一个数叫做这几个数的最大公因数;几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个数叫做这几个数的最小公倍数。
【回顾3】小数点位置移动的规律。
(1)小数点向右移动一位,小数就扩大到原来的10倍;小数点向右移动两位,小数就扩大到原来的100倍……
(2)小数点向左移动一位,小数就缩小到原来的;小数点向左移动两位,小数就缩小到原来的……
【回顾4】正数的大小比较。
正数的大小比较
二、知识应用
1.按要求排序。(学生独立完成,教师点名学生板演,集体订正)
(1)将、、按从大到小的顺序排列起来。
>>
(2)将5.2、5.、5.211按从小到大的顺序排列起来。
5.211<5.2<5.
2.填空。(学生独立完成,教师点名学生回答,集体订正)
(1)把的分母缩小到原来的,要使分数的大小不变,分子应该(缩小到原来的),分数变成( )。
(2)当分数的分子加上4时,为了使分数的大小不变,分母要加上( 18 )。
(3)60的所有因数有(1、2、3、4、5、6、10、12、15、20、30、60),其中质数有( 2、3、5 )。
三、巩固反馈
1.75和15的最大公因数是( 15 ),最小公倍数是( 75 )。
2.判断快车。(点名学生回答,给出判断结果及理由)
(1)若x÷y=2020(x、y是自然数,y≠0),则x是2020的倍数。(?)
(2)最小的奇数是1,最小的偶数是2。(?)
3.在里填上“>”或“<”。(学生齐答,集体订正)
1249<1250
3.11>31.1%
9.08>8.19
>
62830400<628030400
四、课堂小结
通过今天的学习,你掌握了什么?
板书设计
数的认识(2)
教学反思
1.经历知识整理过程。
在课堂上,应该让学生经历知识的整理过程,让学生掌握整理的方法。可以要求学生亲自参与知识的整理过程,这样不但加深了学生对知识的理解,还能从中掌握复习知识的方法,这样有利于学生对知识的复习。
2.辨清各个概念,揭示概念本质属性。
本节课中的概念较多且容易混淆,比如数位、位数与计数单位,偶数与奇数,因数与倍数,因数与公因数,倍数与公倍数,质数与合数等,教学中多次采用比较的形式,让学生在比较的过程中辨清知识的相同点和不同点,帮助学生形成清晰的概念。我在教学中要求学生对一些重点词和一些重点符号要高度关注,比如:关注省略号的作用,让学生思考省略了什么,通过思考揭示概念的本质属性。
3.突出板书在整理知识中的作用。
在教学中关注板书在整理知识中的作用,多次利用板书来呈现知识的相互联系,使学生可以从板书中理解知识的联系与区别,帮助学生形成清晰的概念。板书还可以给学生提供一个复习提纲,学生可以按照板书的内容组织复习,突出重点,层次清楚,容易达到一个较好的复习效果。
4.加强学生对基本概念的理解与记忆。
只有熟练掌握基础知识和相关概念,学生才能很好地进行判断、分析,才能真正理解并掌握知识及知识间的内在联系与区别。
5.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】要使<<成立,a可以是哪些整数?
分析:7、14、4的最小公倍数是28。把这三个分数通分化成分子是28的分数,即<<。由于分子相同的分数分母大的反而小,则可以得出119<2a<128,各项都除以2就是59.5<a<64,因为a是整数,故a可以是60、61、62、63。
解答:a可以是60、61、62、63。
解法归纳:解答本题的关键是把这几个分数通分化成分子相同的分数,同分子的分数比较大小,分母大的分数反而小。
相关知识阅读
点错的小数点
学习数学不仅解题思路要正确,具体解题过程也不能出错,差之毫厘,往往失之千里。
美国芝加哥一个靠养老金生活的老太太,在医院进行了一次小手术。两星期后,她接到医院寄来的一张账单,款数是63440美元。她看到偌大的数字,不禁大惊失色,导致心脏病突发,倒地身亡。后来,有人向医院一核对,原来是把小数点的位置放错了,实际上只需要付63.44美元。
点错一个小数点,竟要了一条人命。正如牛顿所说:“在数学中,最微小的误差也不能忽略。”
第3课时 数的认识(练习课)
课时目标导航
教学导航
一、教学内容
数的认识的运用练习。(教材第74~75页练习十四第1~6题)
二、教学目标
1.使学生进一步理解和掌握整数、分数、小数、百分数的意义和性质。
2.使学生进一步理解因数、倍数、质数、合数等的意义,能熟练地找出两个数的公因数、公倍数等。
3.熟练掌握2、3、5的倍数的特征,并能正确地解决有关问题。
三、重点难点
重点:巩固整数、分数、小数、百分数的基本性质和概念,学会简单的运用。
难点:了解因数、倍数、合数的概念及其综合运用,从练习中找出2、3、5这三个基本数字的倍数的特征,进行归纳小结。
教学过程
一、基础练习
填一填。(课件出示)
(1)一个数是30的因数,又是2和5的倍数,这个数是( )。
(2)一个数是36的因数,也是2和3的倍数,而且比15小,这个数是( )。
(3)根据25×4=100,可知( )是( )的因数,( )也是( )的因数;( )是( )的倍数,也是( )的倍数。
教师指出:已知a、b、c均为正整数(为了方便,在研究因数和倍数时,所指的数不包括0),且a×b=c,那么c就是a和b的倍数,a和b就是c的因数。倍数和因数是相互依存的。
二、指导练习
1.教学教材第74页练习十四第1题。
本题主要考查学生的记数能力,数字和文字相互转化的综合运用能力。将小数49.7 ℃和零下52.3 ℃用数字进行记录,这考查了正数、负数的记法。(2)(3)小题分别考查因数、倍数的相关概念,“打折”的相关运用。注意记数时,正数前面的“+”可以省略不写出,而负数前面的“-”必须写出来。
教师强调:“打七折”表示现价为原价的70%;因数、倍数均是针对非0的自然数而言的。
2.教学教材第74页练习十四第2题。
本题考查将末尾有多个0的数改写成用“万”或“亿”等作计数单位的数,使得书写更加简单、便捷,比如:中国人口有13.4141亿人。同时必须掌握保留小数位数的方法。
教师强调:亿后面是8个0,当不够时就需要小数点继续左移,处理小数问题;万后面是4个0,其他类推。保留小数一般按照“四舍五入”法进行取舍。
学生独立完成,集体订正。
3.教学教材第74页练习十四第3题。
(1)说出数字含义,题目中2在十位、百分位、分子、百位等不同位置,2的含义就是2所代表数位的含义。因此本题需要同学们熟悉分数、小数、整数的组成,理解数位的含义。
(2)本题属于简单分析题,学生独立完成,集体交流,相互订正。
4.教学教材第75页练习十四第4题。
本题主要考查分数、小数、百分数的相互转化问题。比如:将0.4写成分数为,写成百分数为40%,其余题依此类推。
教师强调:三种数之间的相互转化可以有效地简化综合运用中的计算问题。
5.教学教材第75页练习十四第5题。
(1)考查奇数、偶数、合数、质数、倍数、因数、公因数和公倍数的相关概念,解题前可要求学生进行概念的复述,以便更好地解答此题。
(2)考查了排列的相关知识点,2、3、4、5组成没有重复数字的两位数可以是12种,依次为23、24、25、32、34、35、42、43、45、52、53、54。
(3)根据题目中的要求找出质数、合数、偶数、奇数、倍数和公倍数进行分析解答。
(4)教师强调:分步骤有序地进行解答,并且确保又快又准。
6.教学教材第75页练习十四第6题。
本题是对数的相关概念和性质的辨析题。先组织学生独立思考,然后同桌间互相交流答案,并指出错误的原因是什么,集体订正。
三、巩固练习
1.完成教材第75页“练习十四”第7题。(学生独立完成,集体订正)
(1)0.99999 1 (2) 0
2.完成教材第75页“练习十四”第8题。(学生先独立思考,再小组内交流讨论,教师点名学生回答)
<<<
发现规律:分母与分子的差相等的真分数相比较,分母越大,这个分数就越大。
>
验证:=,=,因为>,所以>。
3.完成教材第75页“练习十四”第9*题。(学生先独立思考,再小组内交流讨论,教师适时提醒:本题需要转换思维,对问题进行转化,运用表内乘法或公倍数的知识解决问题,可不用设未知数列方程解答)
8和10的最小公倍数是40,40+6=46(个),因为40<46<50,所以这箱苹果有46个。
四、课堂小结
你能说一说因数和公因数、倍数和公倍数有什么联系和区别吗?在我们生活中有哪些运用?
板书设计
数的认识(练习课)
第1题:(1)49.7 -52.3 (2)b a (3)70 30
第2题:(1)13.4 12.2 (2)1707.5 937.3
第3题:2个十 2个百分之一 2个 2个百
第4题: 40% 0.75 75% 0.8
第5题:12个 (1)23、25、35、43、45、53是奇数;24、32、34、42、52、54是偶数。
(2)23、43、53是质数;24、25、32、34、35、42、45、52、54是合数。
(3)32、42、52、24、34、54是2的倍数;24、42、45、54是3的倍数;25、35、45是5的倍数。
(4)24、42、54 45
第6题:(1)? (2)? (3)? (4)? (5)?
教学反思
1.本节课是练习课,是针对数的认识的系统练习。
在整体的练习中我发挥了学生的主体作用,让他们担任解决问题的主角。另外一方面我强调循序渐进的复习模式,让学生在练习中体会和巩固这些数的意义和性质。但是学生作业中的问题特别多:(1)质数和合数分辨不清,51和91被许多学生当成质数;(2)写50以内的质数,错得太多,不是多写就是少写;(3)与奇数、偶数混合后的判断题出错多。为此要让学生深刻理解质数、合数、奇数、偶数各自的概念,掌握各自的判断方法,也要让学生背一背质数表,帮助学生快速辨别质数,还要告诫学生要细心,要有耐心和学好数学的信心。应再额外教给学生判断质数的简便有效方法:依次用2,3,5,7,11等质数去除这个数,看有没有余数,如91除以7等于13,121除以11等于11。
在分数、小数、百分数等简单的数的改写及转化中,学生掌握得还是非常熟练的,值得肯定。
2.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】甲、乙、丙三人打靶,每人打三枪,三人各自中靶的环数之积都是60,按个人中靶的总环数由高到低排,依次是甲、乙、丙。他们中有一人打中4环,打中4环的那一枪是谁打的?(环数是不超过10的自然数)
分析:60的因数有1、2、3、4、5、6、10、12、15、20、30、60,其中小于等于10的3个因数的积为60的有60=1×6×10,60=2×3×10,60=2×5×6,60=4×3×5。
每一种情况打中的环数分别为1+6+10=17(环),2+3+10=15(环),2+5+6=13(环),4+3+5=12(环)。
按中靶数的高低排列为17、15、13、12。
由于甲、乙、丙三人按个人中靶的总环数由高到低排列,依次是甲、乙、丙,且有一人打中4环,所以靶子上打中4环的那一枪只能是丙打的。
解答:60=1×6×10=2×3×10=2×5×6=4×3×5
在这4种情况中,总环数分别为17、15、13、12。由于三个人按个人中靶的总环数由高到低排列依次是甲、乙、丙,且有一人打中4环,所以靶子上打中4环的那一枪是丙打的。
答:打中4环的那一枪是丙打的。
解法归纳:找到乘积是60(因数是不超过10的自然数)的所有情况,从而找出每个人的打靶环数的可能情况,再根据三个人按个人中靶的总环数由高到低排列依次是甲、乙、丙确定情况。
