六年级数学下册教案圆锥人教版(3课时)
文档属性
| 名称 | 六年级数学下册教案圆锥人教版(3课时) |

|
|
| 格式 | doc | ||
| 文件大小 | 371.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
2 圆 锥
第1课时 圆锥的认识
课时目标导航
教学导航
一、教学内容
圆锥的认识。(教材第31~32页例1)
二、教学目标
1.初步认识圆锥,掌握圆锥的特征,知道圆锥各部分的名称。
2.理解圆锥的高的概念,了解圆锥的高的测量方法。
3.在探究活动中培养观察、概括和动手操作能力,发展空间观念。
三、重点难点
重点:掌握圆锥的特征。
难点:掌握圆锥的高的测量方法。
四、教学准备
教师准备:圆柱、圆锥模型、硬纸板、刻度尺。
学生准备:刻度尺。
教学过程
一、复习引入
(出示一个圆柱模型)
师:这是一个圆柱,谁能说说它有什么特征?(点名学生回答)
师:什么叫圆柱的高?圆柱有几条高?圆柱的高可以怎样测量?
学生思考,小组内交流。
(课件出示教材第31页图片)
师:这些物体的形状都有什么共同特点?
学生小组内讨论、交流。
课件演示从物体中抽象出圆锥的图形,并标明“圆锥”。
师:这些物体的形状都是圆锥体,简称圆锥。你还见过哪些圆锥形的物体?
学生结合生活经验举例,巩固对圆锥形的认识。
师:这节课我们就一起来认识圆锥。(板书课题:圆锥的认识)
二、学习新课
1.圆锥的特征及各部分名称。
(给各小组分发圆锥模型)
师:观察老师给大家发的圆锥模型,说说它有什么特点?
组织学生观察,发现圆锥的特征,集体汇报。(同时教师在黑板上画出一个圆锥)
明确:①圆锥有一个顶点,它的底面是一个圆。(在图上标出顶点,底面及其圆心O)
②圆锥有一个曲面,圆锥的这个曲面叫做侧面。
③从圆锥的顶点到底面圆心的距离叫做高。
(课件演示画出圆锥的母线)
师:沿着圆锥侧面上的这些线是圆锥的高吗?
学生思考,交流、讨论。
教师总结:圆锥的高是圆锥顶点到底面的距离,即圆锥顶点与底面圆心的连线,所以圆锥只有一条高。(板书)
2.测量圆锥的高。
师:同学们,你能测量出手中圆锥的高是多少吗?
学生思考,讨论、交流。
师:由于圆锥的高在它的内部,我们不能直接量出它的长度,这就需要借助一块平板来测量。
课件演示测量过程,教师叙述:
①先把圆锥的底面放平;
②用一硬纸平板水平地放在圆锥的顶点上面;
③竖直地量出平板和底面之间的距离。
小组内互相配合,动手测量手中圆锥的高。
3.旋转形成的圆锥。
师:我们知道一个长方形通过旋转,可以形成一个圆柱。那么将直角三角形纸片绕着一条直角边旋转,会形成什么形状?
通过操作,使学生发现转动出来的是圆锥,并从旋转的角度认识圆锥。
三、巩固反馈
1.完成教材第32页的“做一做”。(点名学生手持圆锥模型说一说)
2.完成教材第35页“练习六”第1、2题。
第1题:天坛由圆锥和圆柱组成;蒙古包由圆柱和圆锥组成;香水瓶由长方体和圆柱组成;建筑物由圆柱、圆锥和长方体组成。
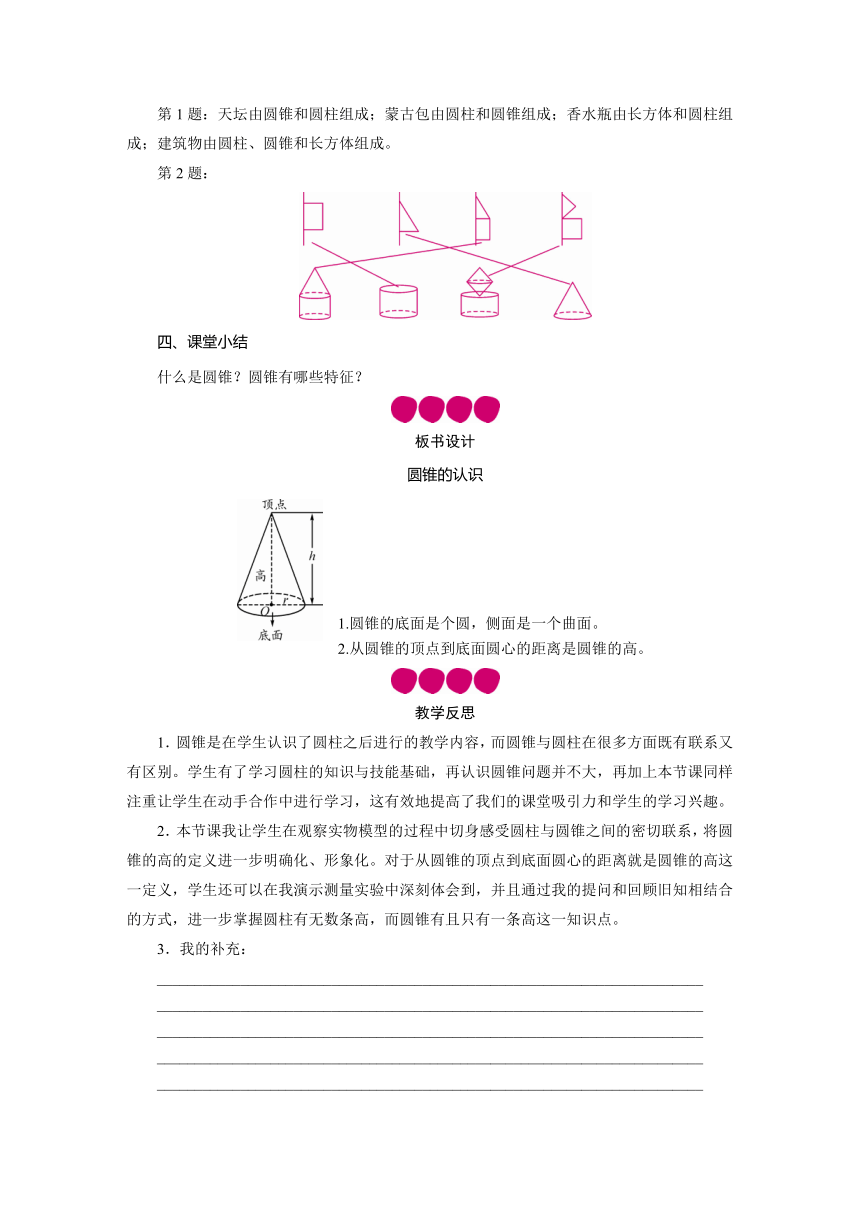
第2题:
四、课堂小结
什么是圆锥?圆锥有哪些特征?
板书设计
圆锥的认识
教学反思
1.圆锥是在学生认识了圆柱之后进行的教学内容,而圆锥与圆柱在很多方面既有联系又有区别。学生有了学习圆柱的知识与技能基础,再认识圆锥问题并不大,再加上本节课同样注重让学生在动手合作中进行学习,这有效地提高了我们的课堂吸引力和学生的学习兴趣。
2.本节课我让学生在观察实物模型的过程中切身感受圆柱与圆锥之间的密切联系,将圆锥的高的定义进一步明确化、形象化。对于从圆锥的顶点到底面圆心的距离就是圆锥的高这一定义,学生还可以在我演示测量实验中深刻体会到,并且通过我的提问和回顾旧知相结合的方式,进一步掌握圆柱有无数条高,而圆锥有且只有一条高这一知识点。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一个圆锥的底面周长是15.7 cm,高是3 cm。从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
分析:从圆锥的顶点沿着高把它切成两半后,表面积比原来圆锥的表面积增加了2个以圆锥的底面直径为底,以圆锥的高为高的三角形的面积,由此利用圆锥的底面周长求出它的底面直径即可解决问题.
解答:圆锥的底面直径:15.7÷3.14=5(cm)
切割后表面积增加了:5×3÷2×2=15(cm2)
答:表面积之和比原圆锥表面积增加了15 cm2。
相关知识阅读
用卡纸做圆锥模型
工具:圆规、剪刀、卡纸、胶带、直尺。
步骤:(1)用圆规在纸上画两个大小不等的圆,且小圆的半径等于大圆的一半。
(2)用剪刀剪下大圆的一半,作为圆锥的侧面,以圆心为中心,用胶带将两条半径粘在一起。
(3)用剪刀剪下整个小圆,作为圆锥的底面,用胶带将圆锥的侧面和底面粘在一起。这样,一个圆锥模型就做好了。
第2课时 圆锥的体积
课时目标导航
教学导航
一、教学内容
圆锥的体积。(教材第33~34页例2、例3)
二、教学目标
1.理解和掌握圆锥体积的计算方法,并能运用公式解决简单的实际问题。
2.经历圆锥体积计算公式的推导过程,进一步理解圆锥与圆柱的联系,培养推理思想。
3.体验发现知识的乐趣,激发学习的兴趣,感受数学与生活的联系,培养应用数学的意识。
三、重点难点
重点:理解圆锥体积公式的推导过程,掌握圆锥体积的计算公式。
难点:运用圆锥体积的计算公式解决简单的实际问题。
四、教学准备
教师准备:课件PPT、圆柱形容器、圆锥形容器、沙子、直尺。
学生准备:圆柱形容器、圆锥形容器、沙子、直尺。
教学过程
一、情境引入
(课件出示雪糕、甜筒图片)
师:同学们在夏天一定都吃过雪糕和甜筒吧,它们都是什么形状的呢?
激发学生兴趣,举手回答。
师:那么你能利用数学知识计算出它们的体积吗?
学生交流、讨论,得出:雪糕一般是长方体的,可以测量出它的长、宽、高,从而计算它的体积。
师:甜筒是圆锥形的,圆锥的体积应该怎样计算呢?今天我们就一起来学习圆锥的体积。(板书课题:圆锥的体积)
二、学习新课
1.探究圆锥的体积公式。
(1)利用试验的方法探究圆锥的体积的计算方法。
①每组同学准备两个等底等高的圆锥形容器、圆柱形容器和一些沙土。
②先将圆柱形的(或圆锥形的)容器里装满沙土(用直尺将多余的沙土刮掉),倒入圆锥形的(或圆柱形的)容器里。
(2)学生汇报试验结果。
①把圆锥装满沙子,再倒进圆柱里,三次刚好装满。
②把圆柱装满沙子,再往圆锥里倒,正好倒了三次。
师:通过试验,你发现等底等高的圆锥、圆柱的体积有什么关系?
小组内讨论、交流,汇报结论。
教师总结:圆柱的体积等于和它等底等高的圆锥的体积的3倍或圆锥的体积等于和它等底等高的圆柱的体积的。
师:“圆锥体积是圆柱体积的”,这句话对吗?
学生思考,点名学生回答。
教师强调:只有在等底等高的条件下才是对的。
师:你能用字母表示出它们的关系吗?
学生小组交流,并汇报:V圆锥=V圆柱=Sh。(板书)
2.教学教材第34页例3。
(课件出示教材第34页例3)
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?
组织学生认真读题,理解题意。
师:沙子的体积和质量应该怎么求呢?
学生思考,讨论、交流并汇报。
教师总结:近似圆锥形的沙堆,可用圆锥的体积公式求出沙子的体积,再求出沙子的质量。
学生独立计算,集体订正。(板书)
(1)沙堆底面积:3.14×2=3.14×4=12.56(m2)
(2)沙堆的体积:×12.56×1.5=6.28(m3)
(3)沙堆重:6.28×1.5=9.42(t)
答:这堆沙子的体积大约是6.28 m3,这堆沙子大约重9.42 t。
3.思考。
求圆锥的体积,还可能出现哪些情况?(圆锥的底面积不直接给出)
(1)已知圆锥的底面半径和高,求体积。
(2)已知圆锥的底面直径和高,求体积。
(3)已知圆锥的底面周长和高,求体积。
(4)已知圆柱的底面半径(底面直径、底面周长)和高,求等底等高的圆锥的体积。
三、巩固反馈
1.完成教材第34页“做一做”。(学生独立完成,点名学生板演,教师点评并订正)
第1题:×19×12=76(cm3)
第2题:3.14×(4÷2)2×5××7.8=163.28≈163(g)
2.完成教材第35页“练习六”第4~6题。
第4题:(1)25.12 (2)423.9
第5题:(1)? (2)? (3)?
第6题:3.14×(31.4÷3.14÷2)2×9×=235.5(cm3)
四、课堂小结
如何计算圆锥的体积?
板书设计
圆锥的体积
V圆锥=V圆柱=Sh
例3 (1)沙堆底面积:3.14×2=3.14×4=12.56(m2)
(2)沙堆的体积:×12.56×1.5=6.28(m3)
(3)沙堆重:6.28×1.5=9.42(t)
答:这堆沙子的体积大约是6.28 m3,这堆沙子大约重9.42 t。
教学反思
1.相比于圆柱体积公式的探究,圆锥的体积更加重视以学生自己动手操作为主,学生从试验中探索发现,总结规律,获得圆锥与圆柱体积的关系。教师则是加以引导,对学生易混淆的知识点进行强调。这对学生形成学好数学的信心大有益处。即便是少数学习困难的学生,也能通过这种“玩游戏”的方式学到知识,体验成功的乐趣。
2.有些学生对圆锥体积的认识,可能仅仅停留在游戏中的倍数关系,不能将其转化到数学公式中,这有碍于后续的公式运用,教学过程中应设计由浅入深的练习,如先练习已知底面积的题,再练习已知底面半径、直径乃至周长的题,帮助他们逐步掌握圆锥的体积公式。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一个圆锥和一个圆柱的体积之比为1∶2,底面积之比为4∶3,圆柱的高为12厘米,圆锥的高是多少厘米?
分析:题中只给出了圆锥与圆柱的体积之比、底面积之比,及圆柱的高,而不知道具体的长度,我们可以根据它们的体积比、底面积比设出未知数,用字母表示,再由圆锥的高=圆锥的体积×3÷圆锥的底面积,圆柱的高=圆柱的体积÷圆柱的底面积求解。
解答:设圆锥的体积为x,底面积为4y,则圆柱的体积为2x,底面积为3y。
==
12×=13.5(厘米)
答:圆锥的高是13.5厘米。
相关知识阅读
制作生日帽
想不想做一个漂亮的生日帽呢?今天教你折可以在生日宴会上戴的圆锥帽子——生日帽。你需要准备以下材料:皱纸带、剪刀、直尺、卡片、胶带等。具体步骤为:
(1)首先从卡片上剪取直径为20 cm的半圆形制作最基本的圆锥体,可以根据需要将该尺寸增大或减小。将半圆卷成锥形并用胶带或胶水固定。
(2)接下来可以进行生日帽的设计了。如要制作仿中世纪的圆锥帽子,可以剪取3种颜色的彩色皱纸带,将皱纸带从帽子的顶端穿过,内侧用胶带固定。然后将3种颜色的皱纸带打成辫,把皱纸辫粘贴于圆锥体的底部。
(3)如果要制作小丑帽,可以先剪取3张直径为5 cm的圆形皱纸制作成绒球,然后捏紧每张圆皱纸的中心并搓捻,把多余的纸揉成球状。之后把第1个绒球推入圆锥体的顶端,再小心地在圆锥体的前面开两道细缝,把绒球的中心推入细缝。
第3课时 圆锥(练习课)
课时目标导航
教学导航
一、教学内容
圆锥的运用练习。(教材第35~36页练习六第7~10题)
二、教学目标
1.加深对圆锥的特征和体积公式的理解。
2.通过巩固练习,提高解决与圆锥有关的问题的能力。
3.培养思维能力和综合运用所学知识解决实际问题的能力。
三、重点难点
重点:运用圆锥体积计算公式解决实际问题。
难点:综合运用有关知识解决实际问题。
教学过程
一、基础练习
1.填空。
(1)一个圆锥的体积是18 dm3,高是6 dm,底面积是( )dm2。
(2)等底等高的圆柱和圆锥,如果圆柱的体积是27 cm3,那么圆锥的体积是( )cm3;如果圆锥的体积是27 cm3,那么圆柱的体积是( )cm3。
(3)如图,瓶底的面积与杯口的面积相等,将瓶子中的水倒入杯子中,能倒满( )杯。
2.计算下面圆锥的体积。(单位:cm)
(1)
(2)
3.公园里有一座如图所示的房子,这座房子的体积是多少立方米?
二、指导练习
1.教学教材第35页练习六第7题。
(课件出示教材第35页练习六第7题)
师:已知圆锥的底面周长和高,怎么求体积?
学生思考,点名学生回答。
明确:已知圆锥的底面周长和高,可以利用V=π2h求圆锥的体积。
学生独立列式计算,点名学生板演,教师点评并订正。
2.教学教材第36页练习六第8题。
(课件出示教材第36页练习六第8题)
师:已知圆锥的底面直径和高,怎么求圆锥的体积?
学生思考,点名学生回答。
明确:已知圆锥的底面直径和高,可以利用V=π2h求圆锥的体积。
学生独立列式计算,点名学生汇报,教师订正。
师:求这堆稻谷重多少千克,用什么方法?(乘法)
学生列式计算,点名学生汇报,教师订正。
师:求平均每公顷产稻谷多少千克,用什么方法?(除法)
学生列式计算,点名学生汇报,教师订正。
师:求这些稻谷能卖多少钱,用什么乘什么?(稻谷的质量乘稻谷的单价)
学生计算并汇报,教师订正。
3.教学教材第36页练习六第9题。
(课件出示教材第36页练习六第9题)
师:想一想,等底等高的圆柱和圆柱的体积有什么关系?
学生思考,回答:等底等高的圆柱和圆锥,圆锥的体积是圆柱的。
师:现在圆柱和圆锥的底面积相等,并且体积相等,它们的高相等吗?(不相等)
师:圆柱和圆锥哪个更高?(圆锥)它们的高有怎样的关系呢?
学生思考,讨论交流,小组汇报。
教师总结:等底等体积的圆柱和圆锥,圆锥的高是圆柱的三倍。
学生列式解答,教师板书并订正。
4×3=12(dm)
答:圆锥的高是12 dm。
4.教学教材第36页练习六第10题。
(课件出示教材第36页练习六第10题)
师:圆柱和圆锥的体积相等,高也相等,它们的底面积相等吗?(不相等)
师:圆柱和圆锥的底面积哪个更大?(圆锥的底面积更大)它们的底面积有什么关系?
学生思考,讨论交流,小组汇报。
教师总结:等高等体积的圆柱和圆锥,圆锥的底面积是圆柱的三倍。
学生列式解答,教师板书并订正。
28.26÷3=9.42(cm2)
答:圆柱的底面积是9.42 cm2。
三、巩固练习
完成教材第36页“练习六”第11题。
1000 km2=10亿平方米
220 mm=0.22 m
10×0.22=2.2(亿立方米)
2.2×20%=0.44(亿立方米)
0.44>0.4,能满足。
四、课堂小结
通过本节课的学习,你有什么收获?
板书设计
圆锥(练习课)
第9题:4×3=12(dm)
答:圆锥的高是12 dm。
第10题:28.26÷3=9.42(cm2)
答:圆柱的底面积是9.42 cm2。
教学反思
1.本节课首先通过几道填空题巩固学生对等底等高的圆柱和圆锥体积的“3倍”关系的掌握,并通过计算圆锥体积的基础练习,使学生熟练掌握公式的运用。在指导练习中,结合题中的生活实际,培养学生分析问题的能力,感受数学与生活的紧密联系。
2.在第9、10题的练习中,通过较为复杂的数量关系的分析,引导学生借助模型,充分理解圆柱和圆锥之间体积的特殊关系,进一步提高学生的逻辑推理能力。在此过程中,学生充分思考,培养抽象与概括的能力。练习课不仅是简单重复的运用知识,更是学生各方面素质提升的途径。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一个直角三角形绕一条直角边所在的直线旋转一周,可以得到一个圆锥。有一个直角三角形,两条直角边分别长3厘米和4厘米,则这个直角三角形绕它的两条直角边所在的直线旋转一周形成的两个圆锥中,哪一个圆锥的体积更大?
分析:直角三角形绕直角边所在的直线形成的圆锥,它的高就是做旋转轴的那条直角边,底面半径为另一条直角边,根据圆锥体积公式计算出两个圆锥的体积,再进行比较。
圆锥一 圆锥二
旋转轴 3厘米长的边所在的直线 4厘米长的边所在的直线
高 3厘米 4厘米
底面 半径 4厘米 3厘米
体积 ×3×42×3.14=50.24
(立方厘米) ×4×32×3.14=37.68(立方厘米)
解答:高为3厘米的圆锥:×3×42×3.14=50.24(立方厘米)
高为4厘米的圆锥:×4×32×3.14=37.68(立方厘米)
50.24>37.68
答:高为3厘米的圆锥的体积大一些。
解法归纳:在直角三角形以直角边所在的直线为轴旋转一周形成的两个圆锥中,以较短的那条直角边所在的直线为轴旋转而成的圆锥的体积大一些。
第1课时 圆锥的认识
课时目标导航
教学导航
一、教学内容
圆锥的认识。(教材第31~32页例1)
二、教学目标
1.初步认识圆锥,掌握圆锥的特征,知道圆锥各部分的名称。
2.理解圆锥的高的概念,了解圆锥的高的测量方法。
3.在探究活动中培养观察、概括和动手操作能力,发展空间观念。
三、重点难点
重点:掌握圆锥的特征。
难点:掌握圆锥的高的测量方法。
四、教学准备
教师准备:圆柱、圆锥模型、硬纸板、刻度尺。
学生准备:刻度尺。
教学过程
一、复习引入
(出示一个圆柱模型)
师:这是一个圆柱,谁能说说它有什么特征?(点名学生回答)
师:什么叫圆柱的高?圆柱有几条高?圆柱的高可以怎样测量?
学生思考,小组内交流。
(课件出示教材第31页图片)
师:这些物体的形状都有什么共同特点?
学生小组内讨论、交流。
课件演示从物体中抽象出圆锥的图形,并标明“圆锥”。
师:这些物体的形状都是圆锥体,简称圆锥。你还见过哪些圆锥形的物体?
学生结合生活经验举例,巩固对圆锥形的认识。
师:这节课我们就一起来认识圆锥。(板书课题:圆锥的认识)
二、学习新课
1.圆锥的特征及各部分名称。
(给各小组分发圆锥模型)
师:观察老师给大家发的圆锥模型,说说它有什么特点?
组织学生观察,发现圆锥的特征,集体汇报。(同时教师在黑板上画出一个圆锥)
明确:①圆锥有一个顶点,它的底面是一个圆。(在图上标出顶点,底面及其圆心O)
②圆锥有一个曲面,圆锥的这个曲面叫做侧面。
③从圆锥的顶点到底面圆心的距离叫做高。
(课件演示画出圆锥的母线)
师:沿着圆锥侧面上的这些线是圆锥的高吗?
学生思考,交流、讨论。
教师总结:圆锥的高是圆锥顶点到底面的距离,即圆锥顶点与底面圆心的连线,所以圆锥只有一条高。(板书)
2.测量圆锥的高。
师:同学们,你能测量出手中圆锥的高是多少吗?
学生思考,讨论、交流。
师:由于圆锥的高在它的内部,我们不能直接量出它的长度,这就需要借助一块平板来测量。
课件演示测量过程,教师叙述:
①先把圆锥的底面放平;
②用一硬纸平板水平地放在圆锥的顶点上面;
③竖直地量出平板和底面之间的距离。
小组内互相配合,动手测量手中圆锥的高。
3.旋转形成的圆锥。
师:我们知道一个长方形通过旋转,可以形成一个圆柱。那么将直角三角形纸片绕着一条直角边旋转,会形成什么形状?
通过操作,使学生发现转动出来的是圆锥,并从旋转的角度认识圆锥。
三、巩固反馈
1.完成教材第32页的“做一做”。(点名学生手持圆锥模型说一说)
2.完成教材第35页“练习六”第1、2题。
第1题:天坛由圆锥和圆柱组成;蒙古包由圆柱和圆锥组成;香水瓶由长方体和圆柱组成;建筑物由圆柱、圆锥和长方体组成。
第2题:
四、课堂小结
什么是圆锥?圆锥有哪些特征?
板书设计
圆锥的认识
教学反思
1.圆锥是在学生认识了圆柱之后进行的教学内容,而圆锥与圆柱在很多方面既有联系又有区别。学生有了学习圆柱的知识与技能基础,再认识圆锥问题并不大,再加上本节课同样注重让学生在动手合作中进行学习,这有效地提高了我们的课堂吸引力和学生的学习兴趣。
2.本节课我让学生在观察实物模型的过程中切身感受圆柱与圆锥之间的密切联系,将圆锥的高的定义进一步明确化、形象化。对于从圆锥的顶点到底面圆心的距离就是圆锥的高这一定义,学生还可以在我演示测量实验中深刻体会到,并且通过我的提问和回顾旧知相结合的方式,进一步掌握圆柱有无数条高,而圆锥有且只有一条高这一知识点。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一个圆锥的底面周长是15.7 cm,高是3 cm。从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
分析:从圆锥的顶点沿着高把它切成两半后,表面积比原来圆锥的表面积增加了2个以圆锥的底面直径为底,以圆锥的高为高的三角形的面积,由此利用圆锥的底面周长求出它的底面直径即可解决问题.
解答:圆锥的底面直径:15.7÷3.14=5(cm)
切割后表面积增加了:5×3÷2×2=15(cm2)
答:表面积之和比原圆锥表面积增加了15 cm2。
相关知识阅读
用卡纸做圆锥模型
工具:圆规、剪刀、卡纸、胶带、直尺。
步骤:(1)用圆规在纸上画两个大小不等的圆,且小圆的半径等于大圆的一半。
(2)用剪刀剪下大圆的一半,作为圆锥的侧面,以圆心为中心,用胶带将两条半径粘在一起。
(3)用剪刀剪下整个小圆,作为圆锥的底面,用胶带将圆锥的侧面和底面粘在一起。这样,一个圆锥模型就做好了。
第2课时 圆锥的体积
课时目标导航
教学导航
一、教学内容
圆锥的体积。(教材第33~34页例2、例3)
二、教学目标
1.理解和掌握圆锥体积的计算方法,并能运用公式解决简单的实际问题。
2.经历圆锥体积计算公式的推导过程,进一步理解圆锥与圆柱的联系,培养推理思想。
3.体验发现知识的乐趣,激发学习的兴趣,感受数学与生活的联系,培养应用数学的意识。
三、重点难点
重点:理解圆锥体积公式的推导过程,掌握圆锥体积的计算公式。
难点:运用圆锥体积的计算公式解决简单的实际问题。
四、教学准备
教师准备:课件PPT、圆柱形容器、圆锥形容器、沙子、直尺。
学生准备:圆柱形容器、圆锥形容器、沙子、直尺。
教学过程
一、情境引入
(课件出示雪糕、甜筒图片)
师:同学们在夏天一定都吃过雪糕和甜筒吧,它们都是什么形状的呢?
激发学生兴趣,举手回答。
师:那么你能利用数学知识计算出它们的体积吗?
学生交流、讨论,得出:雪糕一般是长方体的,可以测量出它的长、宽、高,从而计算它的体积。
师:甜筒是圆锥形的,圆锥的体积应该怎样计算呢?今天我们就一起来学习圆锥的体积。(板书课题:圆锥的体积)
二、学习新课
1.探究圆锥的体积公式。
(1)利用试验的方法探究圆锥的体积的计算方法。
①每组同学准备两个等底等高的圆锥形容器、圆柱形容器和一些沙土。
②先将圆柱形的(或圆锥形的)容器里装满沙土(用直尺将多余的沙土刮掉),倒入圆锥形的(或圆柱形的)容器里。
(2)学生汇报试验结果。
①把圆锥装满沙子,再倒进圆柱里,三次刚好装满。
②把圆柱装满沙子,再往圆锥里倒,正好倒了三次。
师:通过试验,你发现等底等高的圆锥、圆柱的体积有什么关系?
小组内讨论、交流,汇报结论。
教师总结:圆柱的体积等于和它等底等高的圆锥的体积的3倍或圆锥的体积等于和它等底等高的圆柱的体积的。
师:“圆锥体积是圆柱体积的”,这句话对吗?
学生思考,点名学生回答。
教师强调:只有在等底等高的条件下才是对的。
师:你能用字母表示出它们的关系吗?
学生小组交流,并汇报:V圆锥=V圆柱=Sh。(板书)
2.教学教材第34页例3。
(课件出示教材第34页例3)
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?
组织学生认真读题,理解题意。
师:沙子的体积和质量应该怎么求呢?
学生思考,讨论、交流并汇报。
教师总结:近似圆锥形的沙堆,可用圆锥的体积公式求出沙子的体积,再求出沙子的质量。
学生独立计算,集体订正。(板书)
(1)沙堆底面积:3.14×2=3.14×4=12.56(m2)
(2)沙堆的体积:×12.56×1.5=6.28(m3)
(3)沙堆重:6.28×1.5=9.42(t)
答:这堆沙子的体积大约是6.28 m3,这堆沙子大约重9.42 t。
3.思考。
求圆锥的体积,还可能出现哪些情况?(圆锥的底面积不直接给出)
(1)已知圆锥的底面半径和高,求体积。
(2)已知圆锥的底面直径和高,求体积。
(3)已知圆锥的底面周长和高,求体积。
(4)已知圆柱的底面半径(底面直径、底面周长)和高,求等底等高的圆锥的体积。
三、巩固反馈
1.完成教材第34页“做一做”。(学生独立完成,点名学生板演,教师点评并订正)
第1题:×19×12=76(cm3)
第2题:3.14×(4÷2)2×5××7.8=163.28≈163(g)
2.完成教材第35页“练习六”第4~6题。
第4题:(1)25.12 (2)423.9
第5题:(1)? (2)? (3)?
第6题:3.14×(31.4÷3.14÷2)2×9×=235.5(cm3)
四、课堂小结
如何计算圆锥的体积?
板书设计
圆锥的体积
V圆锥=V圆柱=Sh
例3 (1)沙堆底面积:3.14×2=3.14×4=12.56(m2)
(2)沙堆的体积:×12.56×1.5=6.28(m3)
(3)沙堆重:6.28×1.5=9.42(t)
答:这堆沙子的体积大约是6.28 m3,这堆沙子大约重9.42 t。
教学反思
1.相比于圆柱体积公式的探究,圆锥的体积更加重视以学生自己动手操作为主,学生从试验中探索发现,总结规律,获得圆锥与圆柱体积的关系。教师则是加以引导,对学生易混淆的知识点进行强调。这对学生形成学好数学的信心大有益处。即便是少数学习困难的学生,也能通过这种“玩游戏”的方式学到知识,体验成功的乐趣。
2.有些学生对圆锥体积的认识,可能仅仅停留在游戏中的倍数关系,不能将其转化到数学公式中,这有碍于后续的公式运用,教学过程中应设计由浅入深的练习,如先练习已知底面积的题,再练习已知底面半径、直径乃至周长的题,帮助他们逐步掌握圆锥的体积公式。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一个圆锥和一个圆柱的体积之比为1∶2,底面积之比为4∶3,圆柱的高为12厘米,圆锥的高是多少厘米?
分析:题中只给出了圆锥与圆柱的体积之比、底面积之比,及圆柱的高,而不知道具体的长度,我们可以根据它们的体积比、底面积比设出未知数,用字母表示,再由圆锥的高=圆锥的体积×3÷圆锥的底面积,圆柱的高=圆柱的体积÷圆柱的底面积求解。
解答:设圆锥的体积为x,底面积为4y,则圆柱的体积为2x,底面积为3y。
==
12×=13.5(厘米)
答:圆锥的高是13.5厘米。
相关知识阅读
制作生日帽
想不想做一个漂亮的生日帽呢?今天教你折可以在生日宴会上戴的圆锥帽子——生日帽。你需要准备以下材料:皱纸带、剪刀、直尺、卡片、胶带等。具体步骤为:
(1)首先从卡片上剪取直径为20 cm的半圆形制作最基本的圆锥体,可以根据需要将该尺寸增大或减小。将半圆卷成锥形并用胶带或胶水固定。
(2)接下来可以进行生日帽的设计了。如要制作仿中世纪的圆锥帽子,可以剪取3种颜色的彩色皱纸带,将皱纸带从帽子的顶端穿过,内侧用胶带固定。然后将3种颜色的皱纸带打成辫,把皱纸辫粘贴于圆锥体的底部。
(3)如果要制作小丑帽,可以先剪取3张直径为5 cm的圆形皱纸制作成绒球,然后捏紧每张圆皱纸的中心并搓捻,把多余的纸揉成球状。之后把第1个绒球推入圆锥体的顶端,再小心地在圆锥体的前面开两道细缝,把绒球的中心推入细缝。
第3课时 圆锥(练习课)
课时目标导航
教学导航
一、教学内容
圆锥的运用练习。(教材第35~36页练习六第7~10题)
二、教学目标
1.加深对圆锥的特征和体积公式的理解。
2.通过巩固练习,提高解决与圆锥有关的问题的能力。
3.培养思维能力和综合运用所学知识解决实际问题的能力。
三、重点难点
重点:运用圆锥体积计算公式解决实际问题。
难点:综合运用有关知识解决实际问题。
教学过程
一、基础练习
1.填空。
(1)一个圆锥的体积是18 dm3,高是6 dm,底面积是( )dm2。
(2)等底等高的圆柱和圆锥,如果圆柱的体积是27 cm3,那么圆锥的体积是( )cm3;如果圆锥的体积是27 cm3,那么圆柱的体积是( )cm3。
(3)如图,瓶底的面积与杯口的面积相等,将瓶子中的水倒入杯子中,能倒满( )杯。
2.计算下面圆锥的体积。(单位:cm)
(1)
(2)
3.公园里有一座如图所示的房子,这座房子的体积是多少立方米?
二、指导练习
1.教学教材第35页练习六第7题。
(课件出示教材第35页练习六第7题)
师:已知圆锥的底面周长和高,怎么求体积?
学生思考,点名学生回答。
明确:已知圆锥的底面周长和高,可以利用V=π2h求圆锥的体积。
学生独立列式计算,点名学生板演,教师点评并订正。
2.教学教材第36页练习六第8题。
(课件出示教材第36页练习六第8题)
师:已知圆锥的底面直径和高,怎么求圆锥的体积?
学生思考,点名学生回答。
明确:已知圆锥的底面直径和高,可以利用V=π2h求圆锥的体积。
学生独立列式计算,点名学生汇报,教师订正。
师:求这堆稻谷重多少千克,用什么方法?(乘法)
学生列式计算,点名学生汇报,教师订正。
师:求平均每公顷产稻谷多少千克,用什么方法?(除法)
学生列式计算,点名学生汇报,教师订正。
师:求这些稻谷能卖多少钱,用什么乘什么?(稻谷的质量乘稻谷的单价)
学生计算并汇报,教师订正。
3.教学教材第36页练习六第9题。
(课件出示教材第36页练习六第9题)
师:想一想,等底等高的圆柱和圆柱的体积有什么关系?
学生思考,回答:等底等高的圆柱和圆锥,圆锥的体积是圆柱的。
师:现在圆柱和圆锥的底面积相等,并且体积相等,它们的高相等吗?(不相等)
师:圆柱和圆锥哪个更高?(圆锥)它们的高有怎样的关系呢?
学生思考,讨论交流,小组汇报。
教师总结:等底等体积的圆柱和圆锥,圆锥的高是圆柱的三倍。
学生列式解答,教师板书并订正。
4×3=12(dm)
答:圆锥的高是12 dm。
4.教学教材第36页练习六第10题。
(课件出示教材第36页练习六第10题)
师:圆柱和圆锥的体积相等,高也相等,它们的底面积相等吗?(不相等)
师:圆柱和圆锥的底面积哪个更大?(圆锥的底面积更大)它们的底面积有什么关系?
学生思考,讨论交流,小组汇报。
教师总结:等高等体积的圆柱和圆锥,圆锥的底面积是圆柱的三倍。
学生列式解答,教师板书并订正。
28.26÷3=9.42(cm2)
答:圆柱的底面积是9.42 cm2。
三、巩固练习
完成教材第36页“练习六”第11题。
1000 km2=10亿平方米
220 mm=0.22 m
10×0.22=2.2(亿立方米)
2.2×20%=0.44(亿立方米)
0.44>0.4,能满足。
四、课堂小结
通过本节课的学习,你有什么收获?
板书设计
圆锥(练习课)
第9题:4×3=12(dm)
答:圆锥的高是12 dm。
第10题:28.26÷3=9.42(cm2)
答:圆柱的底面积是9.42 cm2。
教学反思
1.本节课首先通过几道填空题巩固学生对等底等高的圆柱和圆锥体积的“3倍”关系的掌握,并通过计算圆锥体积的基础练习,使学生熟练掌握公式的运用。在指导练习中,结合题中的生活实际,培养学生分析问题的能力,感受数学与生活的紧密联系。
2.在第9、10题的练习中,通过较为复杂的数量关系的分析,引导学生借助模型,充分理解圆柱和圆锥之间体积的特殊关系,进一步提高学生的逻辑推理能力。在此过程中,学生充分思考,培养抽象与概括的能力。练习课不仅是简单重复的运用知识,更是学生各方面素质提升的途径。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一个直角三角形绕一条直角边所在的直线旋转一周,可以得到一个圆锥。有一个直角三角形,两条直角边分别长3厘米和4厘米,则这个直角三角形绕它的两条直角边所在的直线旋转一周形成的两个圆锥中,哪一个圆锥的体积更大?
分析:直角三角形绕直角边所在的直线形成的圆锥,它的高就是做旋转轴的那条直角边,底面半径为另一条直角边,根据圆锥体积公式计算出两个圆锥的体积,再进行比较。
圆锥一 圆锥二
旋转轴 3厘米长的边所在的直线 4厘米长的边所在的直线
高 3厘米 4厘米
底面 半径 4厘米 3厘米
体积 ×3×42×3.14=50.24
(立方厘米) ×4×32×3.14=37.68(立方厘米)
解答:高为3厘米的圆锥:×3×42×3.14=50.24(立方厘米)
高为4厘米的圆锥:×4×32×3.14=37.68(立方厘米)
50.24>37.68
答:高为3厘米的圆锥的体积大一些。
解法归纳:在直角三角形以直角边所在的直线为轴旋转一周形成的两个圆锥中,以较短的那条直角边所在的直线为轴旋转而成的圆锥的体积大一些。
