备考2021中考数学北师大版九年级上册第六章《反比例函数》复习教学案(含答案)
文档属性
| 名称 | 备考2021中考数学北师大版九年级上册第六章《反比例函数》复习教学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 290.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 18:19:05 | ||
图片预览


文档简介
反比例函数
复习课
【中考知识点】
1.反比例函数意义;
2.反比例函数
反比例函数图象;
3.反比例函数性质;
4.待定系数法确定函数解析式.
【中考课标要求】
考点
课标要求
知识与技能目标
了解
理解
掌握
灵活应用
反比例函数
理解反比例函数意义
∨
会画反比例函数的图象
∨
理解反比例函数的性质
∨
能根据实际问题中的反比例关系用待定系数法确定反比例函数的解析式
∨
∨
【基础知识梳理】
1.反比例函数的概念
反比例函数y=中的是一个分式,自变量x≠0,函数与x轴、y轴无交点,y=也可写成y=kx-1(k≠0),注意自变量x的指数为-1,
在解决有关自变量指数问题时应特别注意系数k≠0这一限制条件.
2.反比例函数的图象
在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.
3.反比例函数y=中k的意义
注意:反比例函数y=
(k≠0)中比例系数k的几何意义,即过双曲线y=(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.
4.反比例函数经常与一次函数、二次函数等知识相联系.
【例题解析】
1.反比例函数的图象
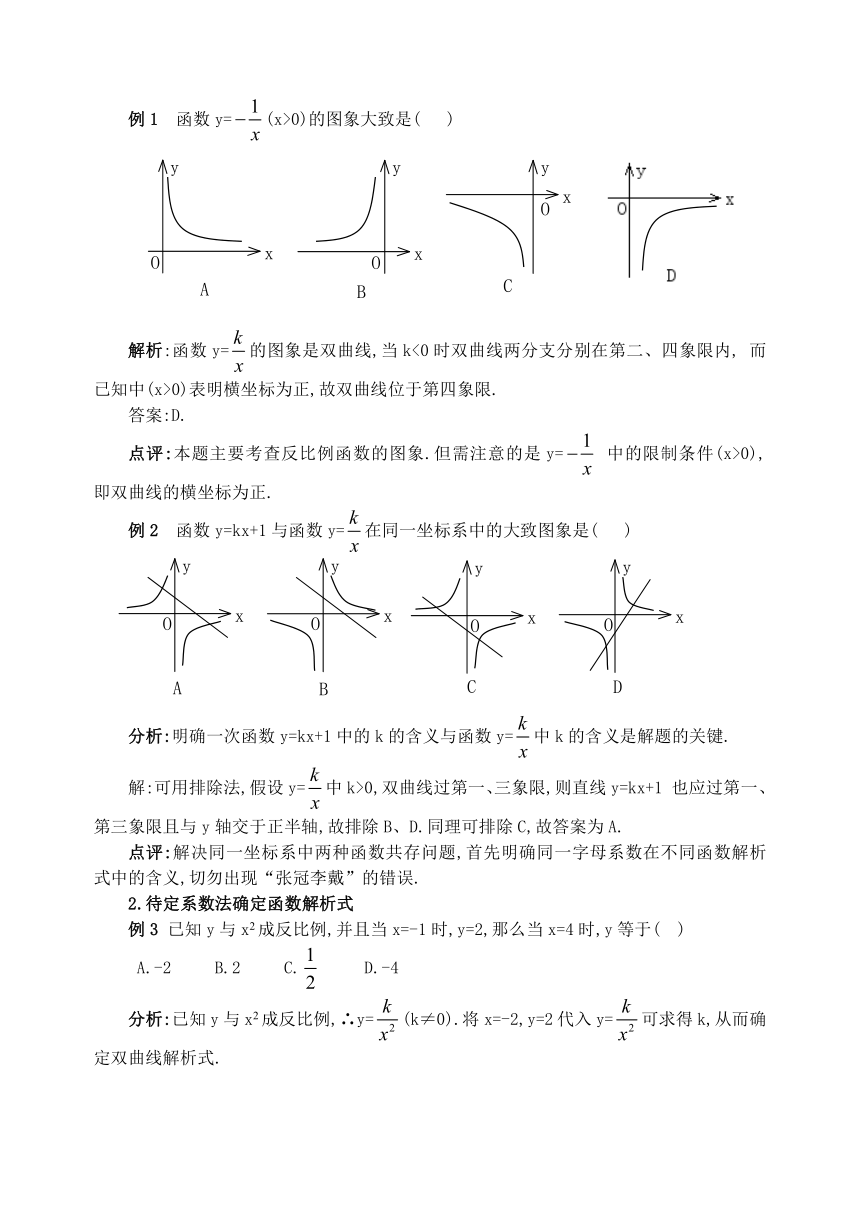
例1
函数y=(x>0)的图象大致是(
)
解析:函数y=的图象是双曲线,当k<0时双曲线两分支分别在第二、四象限内,
而已知中(x>0)表明横坐标为正,故双曲线位于第四象限.
答案:D.
点评:本题主要考查反比例函数的图象.但需注意的是y=
中的限制条件(x>0),
即双曲线的横坐标为正.
例2
函数y=kx+1与函数y=在同一坐标系中的大致图象是(
)
分析:明确一次函数y=kx+1中的k的含义与函数y=中k的含义是解题的关键.
解:可用排除法,假设y=中k>0,双曲线过第一、三象限,则直线y=kx+1
也应过第一、第三象限且与y轴交于正半轴,故排除B、D.同理可排除C,故答案为A.
点评:解决同一坐标系中两种函数共存问题,首先明确同一字母系数在不同函数解析式中的含义,切勿出现“张冠李戴”的错误.
2.待定系数法确定函数解析式
例3
已知y与x2成反比例,并且当x=-1时,y=2,那么当x=4时,y等于(
)
A.-2
B.2
C.
D.-4
分析:已知y与x2成反比例,∴y=(k≠0).将x=-2,y=2代入y=可求得k,从而确定双曲线解析式.
解:∵y与x2成反比例,∴y=
(k≠0).
当x=-2时,y=2,∴2=,k=8
∴y=,把x=4代入y=
得y=.
故答案为C.
点评:此题主要考查反比例函数概念及待定系数法确定函数解析式.
3.反比例函数的应用
例4如图所示,已知一次函数y=kx+b(k≠0)的图象与x
轴、y轴分别交于A、B两点,且与反比例函数y=
(m≠0)的图象在第一象限交于C点,
CD垂直于x轴,垂足为D.若OA=OB=OD=1,
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
分析:(1)由OA=OB=OD=1可确定A、B、D三点坐标.
(2)将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,
由C点在一次函数的图象上可确定C点坐标,将C点坐标代入y=可确定反比例函数的解析式.
解:(1)∵OA=OB=OD=1,∴点A、B、D的坐标分别为A(-1,0),B(0,1),C(1,0).
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴,解得,
∴一次函数的解析式为y=x+1.
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2)
.
又∵点C在反比例函数y=(m≠0)的图象上,m=2.
∴反比例函数的解析式为y=.
【历年考点解析】
考点1:反比例函数的概念
例1近视眼镜的度数(度)与镜片焦距成反比例,已知400度近视眼镜镜片的焦距为0.25,则与的函数关系式为________.
【方法导引】:形如()的函数叫反比例函数.确定反比例函数的解析式,关键是确定反比例系数.
【解答】:
设与的函数关系式为,
把,代入上式,得
,解得.
因此,与的函数关系式为.
【练习1】:已知点(1,2)在反比例函数的图象上,则该反比例函数的解析式为_________.(答案:)
考点2:反比例函数的图象
例2如图1,双曲线的一个分支为(
)
A.
①
B.②
C.③
D.④
图1
【方法导引】:对于双曲线:当时,图象的两个分支在第一、三象限;当时,
图象的两个分支在第二、四象限.同时要注意,当越大,变化的趋势越快,反之越慢.
【解答】:因为,所以双曲线的一个分支应在第一象限,
又知在双曲线上,
故选D.
【练习2】函数与在同一坐标系中的图象可能是(
).
A
B
C
D
(答案:
A
)
考点3
.反比例函数的性质
例3若、、三点都在函数的图象上,则的大小关系是(
)
A.
B.
C.
D..
【方法导引】:对于反比例函数:当时,在每一个象限内,随的增大而减小;当时,在每一个象限内,随的增大而增大.
【解答】:因为,A、B、C三点在同一个象限内,且
所以,.故选B.
想一想:此题还可以怎样解答?
【练习3】:若
,)三点都在函数的图象上,则的大小关系为(
)
A.;
B.;
C.
D.
(答案:B)
考点4:反比例函数的应用
例4某种蓄电池的电压为定值,使用此电源时,电流与可变电阻之间的函数关系如图2所示,当用电器的电流为10A时,用电器的可变电阻为_____.
【方法导引】:先据函数图象,利用待定系数法求出(A)与电阻)的函数关系式,再将代入所求的关系式求出电阻的值.
图2
图3
【解答】:观察图象可知,电流与电阻成反比例函数关系,于是,设,
把代入上式得:
即.
所以,当A时,.
【练习4】在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积时,气体的密度ρ也随之改变.ρ与在一定范围内满足ρ,它的图象如图3所示,则该气体的质量为(
)
A.
B.
C.
D.
7.
(答案:D)
考点5.以反比例函数和一次函数为基架的综合题.
例5.如图4,一次函数的图象与反比例函数图象交于A(-2,1)、B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
【方法导引】:先将交点A的坐标代入反比例函数中,求出反比例函数解析式;再将点B的坐标代入反比例函数关系式中,可求出B点的纵坐标,最后将A、B的坐标代入一次函数中求出,也即是求出一次函数解析式.
求“使一次函数的值大于反比例函数的值的x的取值范围”,也就是求直线上的纵坐标大于双曲线上的纵坐标的横坐标的取值范围.
(
O
A
B
x
y
)
图4
图5
【解答】:(1)将点A(-2,1)代入中得:,
所以
因此,反比例函数解析式为
又将
B(1,n)代入得,所以B(1,-2)
将A(-2,1),B(1,-2)分别代入求得
因此,所求一次函数的解析式为y=-x-1
(2)x<-2或0【练习5】直线y=k1x+b与双曲线y=只有—个交点A(1,2),且与x轴、y轴分别交于B,C
两点AD垂直平分OB,垂足为D,(如图5)求直线、双曲线的解析式.
(答案:).
复习课
【中考知识点】
1.反比例函数意义;
2.反比例函数
反比例函数图象;
3.反比例函数性质;
4.待定系数法确定函数解析式.
【中考课标要求】
考点
课标要求
知识与技能目标
了解
理解
掌握
灵活应用
反比例函数
理解反比例函数意义
∨
会画反比例函数的图象
∨
理解反比例函数的性质
∨
能根据实际问题中的反比例关系用待定系数法确定反比例函数的解析式
∨
∨
【基础知识梳理】
1.反比例函数的概念
反比例函数y=中的是一个分式,自变量x≠0,函数与x轴、y轴无交点,y=也可写成y=kx-1(k≠0),注意自变量x的指数为-1,
在解决有关自变量指数问题时应特别注意系数k≠0这一限制条件.
2.反比例函数的图象
在用描点法画反比例函数y=的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.
3.反比例函数y=中k的意义
注意:反比例函数y=
(k≠0)中比例系数k的几何意义,即过双曲线y=(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.
4.反比例函数经常与一次函数、二次函数等知识相联系.
【例题解析】
1.反比例函数的图象
例1
函数y=(x>0)的图象大致是(
)
解析:函数y=的图象是双曲线,当k<0时双曲线两分支分别在第二、四象限内,
而已知中(x>0)表明横坐标为正,故双曲线位于第四象限.
答案:D.
点评:本题主要考查反比例函数的图象.但需注意的是y=
中的限制条件(x>0),
即双曲线的横坐标为正.
例2
函数y=kx+1与函数y=在同一坐标系中的大致图象是(
)
分析:明确一次函数y=kx+1中的k的含义与函数y=中k的含义是解题的关键.
解:可用排除法,假设y=中k>0,双曲线过第一、三象限,则直线y=kx+1
也应过第一、第三象限且与y轴交于正半轴,故排除B、D.同理可排除C,故答案为A.
点评:解决同一坐标系中两种函数共存问题,首先明确同一字母系数在不同函数解析式中的含义,切勿出现“张冠李戴”的错误.
2.待定系数法确定函数解析式
例3
已知y与x2成反比例,并且当x=-1时,y=2,那么当x=4时,y等于(
)
A.-2
B.2
C.
D.-4
分析:已知y与x2成反比例,∴y=(k≠0).将x=-2,y=2代入y=可求得k,从而确定双曲线解析式.
解:∵y与x2成反比例,∴y=
(k≠0).
当x=-2时,y=2,∴2=,k=8
∴y=,把x=4代入y=
得y=.
故答案为C.
点评:此题主要考查反比例函数概念及待定系数法确定函数解析式.
3.反比例函数的应用
例4如图所示,已知一次函数y=kx+b(k≠0)的图象与x
轴、y轴分别交于A、B两点,且与反比例函数y=
(m≠0)的图象在第一象限交于C点,
CD垂直于x轴,垂足为D.若OA=OB=OD=1,
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
分析:(1)由OA=OB=OD=1可确定A、B、D三点坐标.
(2)将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,
由C点在一次函数的图象上可确定C点坐标,将C点坐标代入y=可确定反比例函数的解析式.
解:(1)∵OA=OB=OD=1,∴点A、B、D的坐标分别为A(-1,0),B(0,1),C(1,0).
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴,解得,
∴一次函数的解析式为y=x+1.
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2)
.
又∵点C在反比例函数y=(m≠0)的图象上,m=2.
∴反比例函数的解析式为y=.
【历年考点解析】
考点1:反比例函数的概念
例1近视眼镜的度数(度)与镜片焦距成反比例,已知400度近视眼镜镜片的焦距为0.25,则与的函数关系式为________.
【方法导引】:形如()的函数叫反比例函数.确定反比例函数的解析式,关键是确定反比例系数.
【解答】:
设与的函数关系式为,
把,代入上式,得
,解得.
因此,与的函数关系式为.
【练习1】:已知点(1,2)在反比例函数的图象上,则该反比例函数的解析式为_________.(答案:)
考点2:反比例函数的图象
例2如图1,双曲线的一个分支为(
)
A.
①
B.②
C.③
D.④
图1
【方法导引】:对于双曲线:当时,图象的两个分支在第一、三象限;当时,
图象的两个分支在第二、四象限.同时要注意,当越大,变化的趋势越快,反之越慢.
【解答】:因为,所以双曲线的一个分支应在第一象限,
又知在双曲线上,
故选D.
【练习2】函数与在同一坐标系中的图象可能是(
).
A
B
C
D
(答案:
A
)
考点3
.反比例函数的性质
例3若、、三点都在函数的图象上,则的大小关系是(
)
A.
B.
C.
D..
【方法导引】:对于反比例函数:当时,在每一个象限内,随的增大而减小;当时,在每一个象限内,随的增大而增大.
【解答】:因为,A、B、C三点在同一个象限内,且
所以,.故选B.
想一想:此题还可以怎样解答?
【练习3】:若
,)三点都在函数的图象上,则的大小关系为(
)
A.;
B.;
C.
D.
(答案:B)
考点4:反比例函数的应用
例4某种蓄电池的电压为定值,使用此电源时,电流与可变电阻之间的函数关系如图2所示,当用电器的电流为10A时,用电器的可变电阻为_____.
【方法导引】:先据函数图象,利用待定系数法求出(A)与电阻)的函数关系式,再将代入所求的关系式求出电阻的值.
图2
图3
【解答】:观察图象可知,电流与电阻成反比例函数关系,于是,设,
把代入上式得:
即.
所以,当A时,.
【练习4】在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积时,气体的密度ρ也随之改变.ρ与在一定范围内满足ρ,它的图象如图3所示,则该气体的质量为(
)
A.
B.
C.
D.
7.
(答案:D)
考点5.以反比例函数和一次函数为基架的综合题.
例5.如图4,一次函数的图象与反比例函数图象交于A(-2,1)、B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
【方法导引】:先将交点A的坐标代入反比例函数中,求出反比例函数解析式;再将点B的坐标代入反比例函数关系式中,可求出B点的纵坐标,最后将A、B的坐标代入一次函数中求出,也即是求出一次函数解析式.
求“使一次函数的值大于反比例函数的值的x的取值范围”,也就是求直线上的纵坐标大于双曲线上的纵坐标的横坐标的取值范围.
(
O
A
B
x
y
)
图4
图5
【解答】:(1)将点A(-2,1)代入中得:,
所以
因此,反比例函数解析式为
又将
B(1,n)代入得,所以B(1,-2)
将A(-2,1),B(1,-2)分别代入求得
因此,所求一次函数的解析式为y=-x-1
(2)x<-2或0
两点AD垂直平分OB,垂足为D,(如图5)求直线、双曲线的解析式.
(答案:).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
