四年级数学下册教案-7.2平 移-人教版
文档属性
| 名称 | 四年级数学下册教案-7.2平 移-人教版 |  | |
| 格式 | doc | ||
| 文件大小 | 244.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 20:52:16 | ||
图片预览

文档简介
2 平 移
课时目标导航
教学导航
一、教学内容
平移的方向和距离,画平移后的图形,利用平移解决问题。(教材第86~87页例3、例4)
二、教学目标
1.让学生学会识别和判断一个简单图形在方格纸上平移的方向和距离,能在方格纸上画出一个简单图形沿水平方向、竖直方向平移后的图形。
2.能利用平移知识解决一些简单的实际问题,体会数学的转化思想。
3.进一步积累平移的学习经验,充分感受观察、操作、探索等活动本身的独特价值,增强对数学的好奇心,产生对图形与变换的兴趣。
三、重点难点
重点:能按要求画出简单的平面图形平移后的图形,会根据平移前后的图形判断平移的方向和距离。
难点:利用平移知识解决生活中简单的实际问题。
教学过程
一、情境引入
师:我们已经学移现象,那么怎样才能确定平移的方向和距离呢?如何画平移后的图形呢?本课时我们将继续学习平移的相关知识。
二、学习新课
1.教学教材第86页例3——探究平移的方向和距离。
(课件展示教材第86页例3)
师:读图找出已知条件和所求问题分别是什么?(小组讨论,全班交流)
明确:图中给出了已知图形和图形平移后的虚线图形,要求先画出图形,再判断出图形平移的方向和距离。
师:你是怎样理解“平移的方向”的?(分小组交流、讨论,然后汇报结果)
学生汇报的结果可能为:“平移的方向”是指给出的图形平移的方向。图中箭头所指的方向就是平移的方向。
教师提示:平移时,物体本身方向不会发生改变。
师:“平移的距离”是指什么?(指名学生回答,集体订正)
引导学生明确:“平移的距离”是指已知图形中的某个关键点,从起始位置到终止位置所移动的方格数量。
师:图中给出的已知图形先向上平移5个方格,是怎样得到的?(分小组交流、讨论,然后汇报结果)
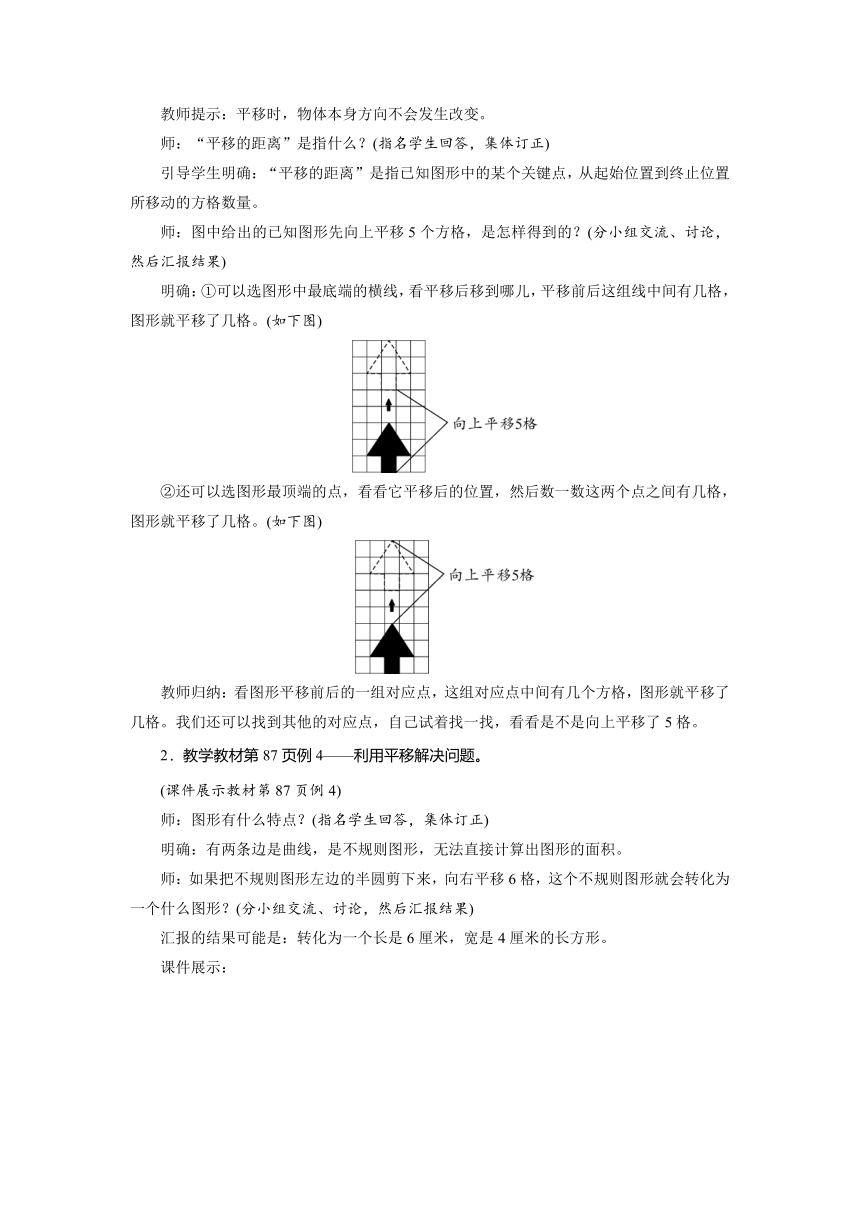
明确:①可以选图形中最底端的横线,看平移后移到哪儿,平移前后这组线中间有几格,图形就平移了几格。(如下图)
②还可以选图形最顶端的点,看看它平移后的位置,然后数一数这两个点之间有几格,图形就平移了几格。(如下图)
教师归纳:看图形平移前后的一组对应点,这组对应点中间有几个方格,图形就平移了几格。我们还可以找到其他的对应点,自己试着找一找,看看是不是向上平移了5格。
2.教学教材第87页例4——利用平移解决问题。
(课件展示教材第87页例4)
师:图形有什么特点?(指名学生回答,集体订正)
明确:有两条边是曲线,是不规则图形,无法直接计算出图形的面积。
师:如果把不规则图形左边的半圆剪下来,向右平移6格,这个不规则图形就会转化为一个什么图形?(分小组交流、讨论,然后汇报结果)
汇报的结果可能是:转化为一个长是6厘米,宽是4厘米的长方形。
课件展示:
师:你会解答了吗?(学生独立解答,全班交流)
教师小结:利用图形在平移的过程中,大小不会改变的特性运用割补的方法,将不规则的图形先分割,再平移,最后补成一个规则的图形求出面积。
三、巩固反馈
1.完成教材第86页“做一做”。(学生独立完成,集体订正)
2.完成教材第87页“做一做”。
画一画略。
面积:9×3=27(平方厘米)
四、课堂小结
1.说一说这堂课的收获。
2.如何确定物体平移的方向和距离?
板书设计
平 移
例3 平移的方向:向上、向下、向左和向右
平移的距离:对应点之间的方格数
例4 平移的应用:不规则图形→规则图形
6×4=24(平方厘米)
答:这个图形的面积是24平方厘米。
教学反思
1.“平移”是生活中处处可见的现象,教学时,先让学生认识平移的方向和距离,再通过师生的共同探究,归纳总结出平移的特点,画出平移后的图形,最后巩固、提高并且运用平移的知识解决简单的实际问题。学生通过动手实际操作,深入理解概念,体现了知识形成的完整过程。
2.本节教学的重点是平移的两个参量:平移的方向和距离,教学的难点是画平移后的图形以及利用平移知识解决简单的实际问题。为此,在教学设计中,环环相扣,由感知到认知、由浅入深、由表及里去引导学生思考和探究,并让学生进行了充分地讨论,从而突出了重点,突破了难点。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】如图是一块长方形草坪,长20米,宽16米,中间有一条宽3米的曲折小路,求小路的面积。
分析:小路是曲折的,不规则图形可以采用平移法转换成规则图形,即将阴影部分往上、往左平移,使空白部分成为一个长方形,小路的面积等于大长方形的面积减去小长方形的面积,如图。
解答:20×16-(20-3)×(16-3)
=320-221
=99(平方米)
答:小路的面积为99平方米。
解法归纳:解此类题时,一般利用平移法将阴影部分进行平移,使不规则图形变为规则图形,再进行相关计算。
相关知识阅读
建筑物的平移
始建于1930年的上海音乐厅是上海高雅音乐的圣殿,数十年来以良好的声乐效果和欧洲古典风格的建筑特色,被誉为“上海的巴黎歌剧院”,具有极高的知名度。
自2002年9月起,为配合城市改造,音乐厅进行了耗资1.2亿的平移改造工程。至2003年7月8日,音乐厅成功地完成了抬升3.38米,向东南方平移66.46米的壮举,在全国建筑平移史上创造了一个奇迹。
经过整体平移之后的上海音乐厅“金色大厅”展示给人们的是一座既折射历史辉煌又焕发时代特色的音乐殿堂,音乐厅舞台、双层观众席、大厅、演员休息厅、金色弧顶灯等所有内部装修焕然一新,金碧辉煌堪称经典。经过此次的平移修整,观众将领略到90岁的音乐厅重焕的青春魅力。
课时目标导航
教学导航
一、教学内容
平移的方向和距离,画平移后的图形,利用平移解决问题。(教材第86~87页例3、例4)
二、教学目标
1.让学生学会识别和判断一个简单图形在方格纸上平移的方向和距离,能在方格纸上画出一个简单图形沿水平方向、竖直方向平移后的图形。
2.能利用平移知识解决一些简单的实际问题,体会数学的转化思想。
3.进一步积累平移的学习经验,充分感受观察、操作、探索等活动本身的独特价值,增强对数学的好奇心,产生对图形与变换的兴趣。
三、重点难点
重点:能按要求画出简单的平面图形平移后的图形,会根据平移前后的图形判断平移的方向和距离。
难点:利用平移知识解决生活中简单的实际问题。
教学过程
一、情境引入
师:我们已经学移现象,那么怎样才能确定平移的方向和距离呢?如何画平移后的图形呢?本课时我们将继续学习平移的相关知识。
二、学习新课
1.教学教材第86页例3——探究平移的方向和距离。
(课件展示教材第86页例3)
师:读图找出已知条件和所求问题分别是什么?(小组讨论,全班交流)
明确:图中给出了已知图形和图形平移后的虚线图形,要求先画出图形,再判断出图形平移的方向和距离。
师:你是怎样理解“平移的方向”的?(分小组交流、讨论,然后汇报结果)
学生汇报的结果可能为:“平移的方向”是指给出的图形平移的方向。图中箭头所指的方向就是平移的方向。
教师提示:平移时,物体本身方向不会发生改变。
师:“平移的距离”是指什么?(指名学生回答,集体订正)
引导学生明确:“平移的距离”是指已知图形中的某个关键点,从起始位置到终止位置所移动的方格数量。
师:图中给出的已知图形先向上平移5个方格,是怎样得到的?(分小组交流、讨论,然后汇报结果)
明确:①可以选图形中最底端的横线,看平移后移到哪儿,平移前后这组线中间有几格,图形就平移了几格。(如下图)
②还可以选图形最顶端的点,看看它平移后的位置,然后数一数这两个点之间有几格,图形就平移了几格。(如下图)
教师归纳:看图形平移前后的一组对应点,这组对应点中间有几个方格,图形就平移了几格。我们还可以找到其他的对应点,自己试着找一找,看看是不是向上平移了5格。
2.教学教材第87页例4——利用平移解决问题。
(课件展示教材第87页例4)
师:图形有什么特点?(指名学生回答,集体订正)
明确:有两条边是曲线,是不规则图形,无法直接计算出图形的面积。
师:如果把不规则图形左边的半圆剪下来,向右平移6格,这个不规则图形就会转化为一个什么图形?(分小组交流、讨论,然后汇报结果)
汇报的结果可能是:转化为一个长是6厘米,宽是4厘米的长方形。
课件展示:
师:你会解答了吗?(学生独立解答,全班交流)
教师小结:利用图形在平移的过程中,大小不会改变的特性运用割补的方法,将不规则的图形先分割,再平移,最后补成一个规则的图形求出面积。
三、巩固反馈
1.完成教材第86页“做一做”。(学生独立完成,集体订正)
2.完成教材第87页“做一做”。
画一画略。
面积:9×3=27(平方厘米)
四、课堂小结
1.说一说这堂课的收获。
2.如何确定物体平移的方向和距离?
板书设计
平 移
例3 平移的方向:向上、向下、向左和向右
平移的距离:对应点之间的方格数
例4 平移的应用:不规则图形→规则图形
6×4=24(平方厘米)
答:这个图形的面积是24平方厘米。
教学反思
1.“平移”是生活中处处可见的现象,教学时,先让学生认识平移的方向和距离,再通过师生的共同探究,归纳总结出平移的特点,画出平移后的图形,最后巩固、提高并且运用平移的知识解决简单的实际问题。学生通过动手实际操作,深入理解概念,体现了知识形成的完整过程。
2.本节教学的重点是平移的两个参量:平移的方向和距离,教学的难点是画平移后的图形以及利用平移知识解决简单的实际问题。为此,在教学设计中,环环相扣,由感知到认知、由浅入深、由表及里去引导学生思考和探究,并让学生进行了充分地讨论,从而突出了重点,突破了难点。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】如图是一块长方形草坪,长20米,宽16米,中间有一条宽3米的曲折小路,求小路的面积。
分析:小路是曲折的,不规则图形可以采用平移法转换成规则图形,即将阴影部分往上、往左平移,使空白部分成为一个长方形,小路的面积等于大长方形的面积减去小长方形的面积,如图。
解答:20×16-(20-3)×(16-3)
=320-221
=99(平方米)
答:小路的面积为99平方米。
解法归纳:解此类题时,一般利用平移法将阴影部分进行平移,使不规则图形变为规则图形,再进行相关计算。
相关知识阅读
建筑物的平移
始建于1930年的上海音乐厅是上海高雅音乐的圣殿,数十年来以良好的声乐效果和欧洲古典风格的建筑特色,被誉为“上海的巴黎歌剧院”,具有极高的知名度。
自2002年9月起,为配合城市改造,音乐厅进行了耗资1.2亿的平移改造工程。至2003年7月8日,音乐厅成功地完成了抬升3.38米,向东南方平移66.46米的壮举,在全国建筑平移史上创造了一个奇迹。
经过整体平移之后的上海音乐厅“金色大厅”展示给人们的是一座既折射历史辉煌又焕发时代特色的音乐殿堂,音乐厅舞台、双层观众席、大厅、演员休息厅、金色弧顶灯等所有内部装修焕然一新,金碧辉煌堪称经典。经过此次的平移修整,观众将领略到90岁的音乐厅重焕的青春魅力。
