四年级数学下册教案-5.1三角形的特性-人教版(2课时)
文档属性
| 名称 | 四年级数学下册教案-5.1三角形的特性-人教版(2课时) |  | |
| 格式 | doc | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 20:57:54 | ||
图片预览



文档简介
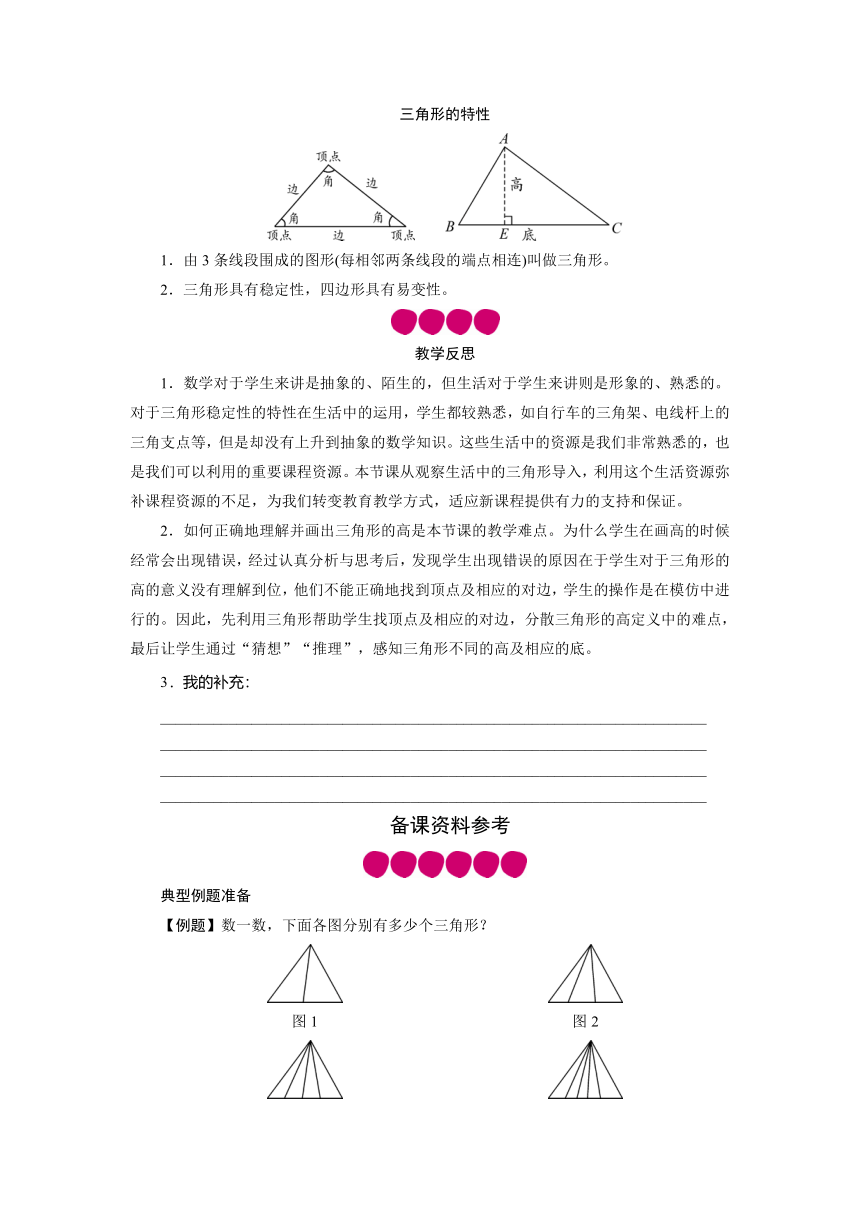
1 三角形的特性
第1课时 三角形的特性
课时目标导航
教学导航
一、教学内容
三角形的特性。(教材第59~61页例1、例2)
二、教学目标
1.通过动手操作和观察比较,使学生理解三角形的概念,认识三角形各部分的名称、三角形的底和高以及其高的画法。
2.通过实践活动,认识三角形的稳定性及其在生活中的应用。
3.提高学生观察、操作的能力和应用数学知识解决实际问题的能力,体验数学与生活的联系,培养学习数学的兴趣。
三、重点难点
重点:理解三角形的概念、掌握三角形的特性。
难点:理解三角形的稳定性和高的画法。
四、教学准备
教师准备:教学课件、直尺、小棒。
学生准备:直尺、小棒。
教学过程
一、情境引入
日常生活中,你见到过哪些三角形?这些三角形都有什么特性呢?今天我们就来一起学习三角形的特性。
二、学习新课
1.教学教材第60页例1——认识三角形及高的画法。
(1)认识三角形。
师:画一个三角形。说一说三角形有几条边,几个角,几个顶点。(课件展示教材第60页例1)
师:你会画三角形吗?在自己的练习本上画出一个三角形。(组织学生动手画一个三角形,并进行展示)
展示学生画的三角形。
图1 图2
图3 图4
师:谁能说说上面的图形哪些是三角形?(指名学生回答)
明确:图3和图4是三角形。
师:图1和图2是三角形吗?为什么?(组织学生讨论,再汇报结果)
明确:图1不是封闭的图形,图2中有一条线不是直线,所以它们都不是三角形。
师:什么样的图形叫做三角形?(让学生尝试总结,教师点评)
师生共同归纳总结:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(2)认识三角形各部分的名称。
师:观察你们所画的三角形,说一说三角形有几条边,几个角,几个顶点。
明确:任意一个三角形都有3条边,3个角,3个顶点。(课件展示教材第60页标有顶点、边、角的三角形图)
明确:组成三角形的三条线段,叫做三角形的边,相邻两条边的交点叫顶点,相邻两条边的夹角叫三角形的内角,简称角。为了表达方便,我们用字母A、B、C分别表示三角形的3个顶点,这个三角形可以表示成三角形ABC。
(3)认识三角形的高。
①认识顶点和对边。(课件展示教材第60页三角形ABC图)
指导学生认识顶点和对边:A点的对边是BC;B点的对边是AC;C点的对边是AB。
②认识三角形的底和高。
指导学生认识三角形的高:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
师:给你一个三角形,你可以画出几条高呢?(组织学生在小组中议一议,动手画一画,并互相交流)
学生在交流中可能会出现给直角三角形和钝角三角形画高的情况,教师根据学生的汇报结果指出:三角形有3条高,直角三角形中直角边上的高是另一条直角边,钝角三角形有两条高在它底边的延长线上。
教师课件展示:三角形高的几种情况。展示三角形的高时,明确三角形的高一般画成虚线。
2.教学教材第61页例2——认识三角形的稳定性。
师:用3根小棒围三角形,用4根小棒围四边形。看看各能围出几个。(小棒的长度都一样)(课件展示教材第61页例2)
(1)学生动手围一围。通过围一围学生总结:用3根同样长的小棒无论怎样摆,最后摆出的结果都是同样形状的三角形。用4根同样长的小棒摆四边形,摆出的形状是不同的,有的是正方形,有的是平行四边形。
师:通过拼摆,你发现了什么?(指名学生回答)
引导学生明确:小棒的长度固定,三角形的形状就固定。四边形的形状是不稳定的。
(2)教师多媒体播放电线杆、自行车和篮球架等三角形应用的图片。
师:为什么这些物体的这些部位要做成三角形?三角形具有什么特性?(组织学生交流,并汇报结果)
教师归纳:三角形具有稳定性。四边形具有易变性。
三、巩固反馈
1.完成教材第60页“做一做”。(组织学生独立完成)
答案:
2.完成教材第61页“做一做”。(指名学生说一说)
答案:略
3.完成教材第65页练习十五第1题。(学生独立完成,集体订正)
第1题:
四、课堂小结
学完这节课,你知道三角形有哪些特性吗?你能说出三角形的稳定性在生活中有哪些应用吗?
板书设计
三角形的特性
1.由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
2.三角形具有稳定性,四边形具有易变性。
教学反思
1.数学对于学生来讲是抽象的、陌生的,但生活对于学生来讲则是形象的、熟悉的。对于三角形稳定性的特性在生活中的运用,学生都较熟悉,如自行车的三角架、电线杆上的三角支点等,但是却没有上升到抽象的数学知识。这些生活中的资源是我们非常熟悉的,也是我们可以利用的重要课程资源。本节课从观察生活中的三角形导入,利用这个生活资源弥补课程资源的不足,为我们转变教育教学方式,适应新课程提供有力的支持和保证。
2.如何正确地理解并画出三角形的高是本节课的教学难点。为什么学生在画高的时候经常会出现错误,经过认真分析与思考后,发现学生出现错误的原因在于学生对于三角形的高的意义没有理解到位,他们不能正确地找到顶点及相应的对边,学生的操作是在模仿中进行的。因此,先利用三角形帮助学生找顶点及相应的对边,分散三角形的高定义中的难点,最后让学生通过“猜想”“推理”,感知三角形不同的高及相应的底。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】数一数,下面各图分别有多少个三角形?
图1 图2
图3 图4
你发现了什么规律吗?说说看。
分析:图1有2个小三角形和1个大三角形,一共是2+1=3(个)三角形;图2有3个小三角形,相邻两个小三角形组成2个三角形,有1个大三角形,共有3+2+1=6(个)三角形;图3有4个小三角形,相邻两个小三角形组成3个三角形,相邻3个三角形组成2个三角形,有1个大三角形,共有4+3+2+1=10(个)三角形;图4有5个小三角形,相邻两个小三角形组成4个三角形,相邻3个三角形组成3个三角形,相邻4个小三角形组成2个三角形;有1个大三角形,共有5+4+3+2+1=15(个)三角形。由此得出规律:若图形中的单个小三角形个数为n,则图形中三角形的总个数就是1+2+3+4+5+…+n。
解答:图1共有2+1=3(个)三角形。
图2共有3+2+1=6(个)三角形。
图3共有4+3+2+1=10(个)三角形。
图4共有5+4+3+2+1=15(个)三角形。
由此得出规律:若图形中的单个小三角形个数为n,则图形中三角形的总个数就是1+2+3+4+…+n。
解法归纳:从三角形的一个顶点向对边引若干条线段,将三角形分成了若干个小三角形,若小三角形的个数为n,则三角形的总个数为1+2+3+4+…+n。
相关知识阅读
能干的设计师——小“3”
一天,小“1”带着几个伙伴在路边竖一根电视天线杆。天线杆竖起来以后,总是晃来晃去,他们急得团团转。
恰巧小“3”路过这里,看见了,赶忙过来说:“这又直又高的电视天线杆光这样竖着不稳定,有倒斜的危险。”
“请问,您有什么好办法吗?”小“1”诚恳地问。
小“3”说:“用三根绳子从杆子的上方向三个方向拉下来,拉紧以后把绳头固定在地面上,固定在地面上的三点能成一个三角形,天线杆就不会晃了。”
“好!”小“1”他们很快动手,把绳子拉好。果然,天线杆不晃动了。“真行!”“这个办法真灵!”大家一起高兴地围着小“3”询问这是为什么。小“3”笑着说:“因为三角形有一个特性,叫做三角形的稳定性。你看,木制的房顶,自行车的三角架,还有高压电线架都是三角形,就是利用这个特性。”
“你真是个能干的设计师。”小“1”称赞小“3”说。小“3”不好意思地说:“不,我们各有所长,要相互学习。”
“哈哈,各有所长,各有所长……”大伙会心地笑了。
第2课时 三角形三条边的关系
课时目标导航
教学导航
一、教学内容
三角形三条边的关系。(教材第62页例3、例4)
二、教学目标
1.知道两点间距离的意义,明白两点之间线段最短的道理。
2.通过操作、探索,发现三角形三边之间的关系:三角形任意两边的和大于第三边。
3.掌握判断三条线段能否构成一个三角形的方法,并能解决有关的问题。
4.提高学生逻辑思维能力,以及培养学生“猜测——验证——总结”的学习习惯。
三、重点难点
重点:知道两点间距离的意义,明白两点之间线段最短的道理。
难点:三角形三边之间的关系。
教学过程
一、情境引入
师:这是小明同学上学的路线。请大家仔细观察,他可以怎样走?在这几条路线中哪条最近?为什么?(课件展示教材第62页例3情境图)
师:要明白这些问题,就要学习本节课的内容,你准备好了吗?(课件展示课题:三角形三条边的关系)
二、学习新课
1.教学教材第62页例3——两点间的距离的意义。
师:小明上学走哪条路最近?(课件展示教材第62页例3情境图)
师:观察情境图说一说,从小明家到学校有几条路线?分别是怎么走的?(分组讨论,指名学生回答)
明确:从小明家到学校有3条路可走。
第一条:家→邮局→学校
第二条:家→学校
第三条:家→商店→学校
师:哪条路最近?(指名学生回答)
明确:家→学校这条路最近。
师:为什么大家都认为中间这条路最近?(小组讨论,学生反馈)
理由1:因为第一条和第三条路线拐弯了,绕远路,所以中间这条最近。
理由2:生活中这样走过,中间的这条路线最短。
理由3:在课本的图中通过测量得出中间的这条路线最短。
……
(引导学生积极发言,教师指导理解有困难的学生)
教师指导学生进行测量,从而明确中间这条路最近。
师:家、邮局、学校,我们可以看作三个点,你能发现它们构成了一个什么图形吗?(让学生结合情境图说一说)
明确:观察情境图可以发现家→邮局→学校可以看成一个三角形,其中家到邮局的距离+邮局到学校的距离>家到学校的距离。家→商店→学校也可以看成一个三角形,家到商店的距离+商店到学校的距离>家到学校的距离。
师:通过上面的观察,你能得出什么结论?
师生共同总结:两点之间,线段最短。
教师指导:在数学上,把连接两点间的线段的长度叫做两点间的距离。
2.教学教材第62页例4——三角形三条边的关系。
(课件展示教材第62页例4)
师:剪出下面4组长度的纸条。(单位:cm)。
(1)6、7、8。
(2)4、5、9。
(3)3、6、10。
(4)8、11、11。
师:用每组纸条摆三角形,哪些能摆出三角形?哪些不能摆出三角形?(学生分小组拼摆三角形,小组讨论,全班交流)
通过拼摆发现,上面的四组纸条有的可以摆成三角形,有的不能摆成三角形,能摆成三角形的是(1)和(4),不能摆成三角形的是(2)和(3)。
师:对比能与不能摆成三角形的三根纸条的长度你能发现什么?(分组讨论,集体订正)
不能摆成三角形的三根纸条中,有两根的长度之和等于或小于第三根,如4+5=9,3+6<10;能摆成三角形的三根纸条中,任意两根长度的和都大于第三根的长度,如6+7>8,8+11>11。
师:你能用自己的语言概括一下上面你的发现吗?(指名学生回答)
师生共同总结:三角形任意两边的和大于第三边。
三、巩固反馈
1.下面每组中的三条线段能否围成一个三角形?说明理由。(学生独立完成)
(1)3 cm、7 cm、5 cm
(2)6 cm、2 cm、2 cm
(3)8 cm、4 cm、4 cm
答案:(1)能 3+5>7 (2)不能 2+2<6 (3)不能 4+4=8
2.从长度分别为3 cm、5 cm、8 cm、4 cm的4根小棒中选出3根,围成一个三角形。你准备怎么选?为什么?(学生分组讨论、交流,派代表反馈,说明解题重点)
答案:5 cm、8 cm、4 cm或者是3 cm、4 cm、5 cm。因为三角形任意两边的和大于第三边。
四、课堂小结
1.说一说这堂课的收获。
2.三角形的三边关系是什么?
板书设计
三角形三条边的关系
例3 两点间的距离:两点间的所有连线中线段最短,这条线段的长度叫做两点间的距离。
例4 可以围成三角形的三边 6+7>8 8+11>11
不可以围成三角形的三边 4+5=9 3+6<10
判断标准:较小的两条线段的和大于第三条线段。
发现:三角形的任意两边的和大于第三边。
教学反思
1.本节课通过让学生仔细观察小明上学的路线图,发现连接小明家、商店、学校三地近似是一个三角形,而连接小明家、邮局、学校三地同样也近似是一个三角形。走中间的这条路实际上就是三角形的一条边,走小明家→商店→学校或走小明家→邮局→学校的路程实际上是三角形的另外两条边的和,发现三角形的两条边的和要比第三边大。这就引出了这节课要探究的问题:是不是所有的三角形的三条边都有这样的关系呢?在探究这个问题时,让每个小组用不同的四组纸条来摆三角形,通过操作让学生发现有的三根纸条不能摆成三角形,有的三根纸条却能摆成三角形,而能摆成三角形的三根小棒都有一个共同规律,由此得出三角形任意两边的和大于第三边。
2.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】把一根12厘米的吸管剪成3段(每段都是整厘米数),摆成一个三角形,共有几种剪法,你能全部列举出来吗?
分析:因为三角形任意两边的和大于第三边,且三条边的总长为12厘米,所以摆成的三角形的最长边<6厘米,即最长边最大是5厘米。将12厘米分成三个整厘米数相加且满足三角形任意两边的和大于第三边的形式为12=3+4+5=4+4+4=2+5+5。
符合题意的三角形各边分别为:①3厘米、4厘米、5厘米;②4厘米、4厘米、4厘米;③2厘米、5厘米、5厘米。
解答:共有3种剪法,可以是3厘米、4厘米、5厘米;4厘米、4厘米、4厘米;2厘米、5厘米、5厘米。
解法归纳:先确定最长边最大的取值,再将12分成三个整数相加且满足三角形任意两边的和大于第三边的形式。
相关知识阅读
三角形任意两边的和大于第三边的原理
有A、B两点,连接AB,得到线段AB(如图1),线段AB外有任意一点C,连接AC、BC,组成三角形ABC(如图2)。由“两点间所有连线中线段最短”可知,AB
图1 图2
第1课时 三角形的特性
课时目标导航
教学导航
一、教学内容
三角形的特性。(教材第59~61页例1、例2)
二、教学目标
1.通过动手操作和观察比较,使学生理解三角形的概念,认识三角形各部分的名称、三角形的底和高以及其高的画法。
2.通过实践活动,认识三角形的稳定性及其在生活中的应用。
3.提高学生观察、操作的能力和应用数学知识解决实际问题的能力,体验数学与生活的联系,培养学习数学的兴趣。
三、重点难点
重点:理解三角形的概念、掌握三角形的特性。
难点:理解三角形的稳定性和高的画法。
四、教学准备
教师准备:教学课件、直尺、小棒。
学生准备:直尺、小棒。
教学过程
一、情境引入
日常生活中,你见到过哪些三角形?这些三角形都有什么特性呢?今天我们就来一起学习三角形的特性。
二、学习新课
1.教学教材第60页例1——认识三角形及高的画法。
(1)认识三角形。
师:画一个三角形。说一说三角形有几条边,几个角,几个顶点。(课件展示教材第60页例1)
师:你会画三角形吗?在自己的练习本上画出一个三角形。(组织学生动手画一个三角形,并进行展示)
展示学生画的三角形。
图1 图2
图3 图4
师:谁能说说上面的图形哪些是三角形?(指名学生回答)
明确:图3和图4是三角形。
师:图1和图2是三角形吗?为什么?(组织学生讨论,再汇报结果)
明确:图1不是封闭的图形,图2中有一条线不是直线,所以它们都不是三角形。
师:什么样的图形叫做三角形?(让学生尝试总结,教师点评)
师生共同归纳总结:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(2)认识三角形各部分的名称。
师:观察你们所画的三角形,说一说三角形有几条边,几个角,几个顶点。
明确:任意一个三角形都有3条边,3个角,3个顶点。(课件展示教材第60页标有顶点、边、角的三角形图)
明确:组成三角形的三条线段,叫做三角形的边,相邻两条边的交点叫顶点,相邻两条边的夹角叫三角形的内角,简称角。为了表达方便,我们用字母A、B、C分别表示三角形的3个顶点,这个三角形可以表示成三角形ABC。
(3)认识三角形的高。
①认识顶点和对边。(课件展示教材第60页三角形ABC图)
指导学生认识顶点和对边:A点的对边是BC;B点的对边是AC;C点的对边是AB。
②认识三角形的底和高。
指导学生认识三角形的高:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
师:给你一个三角形,你可以画出几条高呢?(组织学生在小组中议一议,动手画一画,并互相交流)
学生在交流中可能会出现给直角三角形和钝角三角形画高的情况,教师根据学生的汇报结果指出:三角形有3条高,直角三角形中直角边上的高是另一条直角边,钝角三角形有两条高在它底边的延长线上。
教师课件展示:三角形高的几种情况。展示三角形的高时,明确三角形的高一般画成虚线。
2.教学教材第61页例2——认识三角形的稳定性。
师:用3根小棒围三角形,用4根小棒围四边形。看看各能围出几个。(小棒的长度都一样)(课件展示教材第61页例2)
(1)学生动手围一围。通过围一围学生总结:用3根同样长的小棒无论怎样摆,最后摆出的结果都是同样形状的三角形。用4根同样长的小棒摆四边形,摆出的形状是不同的,有的是正方形,有的是平行四边形。
师:通过拼摆,你发现了什么?(指名学生回答)
引导学生明确:小棒的长度固定,三角形的形状就固定。四边形的形状是不稳定的。
(2)教师多媒体播放电线杆、自行车和篮球架等三角形应用的图片。
师:为什么这些物体的这些部位要做成三角形?三角形具有什么特性?(组织学生交流,并汇报结果)
教师归纳:三角形具有稳定性。四边形具有易变性。
三、巩固反馈
1.完成教材第60页“做一做”。(组织学生独立完成)
答案:
2.完成教材第61页“做一做”。(指名学生说一说)
答案:略
3.完成教材第65页练习十五第1题。(学生独立完成,集体订正)
第1题:
四、课堂小结
学完这节课,你知道三角形有哪些特性吗?你能说出三角形的稳定性在生活中有哪些应用吗?
板书设计
三角形的特性
1.由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
2.三角形具有稳定性,四边形具有易变性。
教学反思
1.数学对于学生来讲是抽象的、陌生的,但生活对于学生来讲则是形象的、熟悉的。对于三角形稳定性的特性在生活中的运用,学生都较熟悉,如自行车的三角架、电线杆上的三角支点等,但是却没有上升到抽象的数学知识。这些生活中的资源是我们非常熟悉的,也是我们可以利用的重要课程资源。本节课从观察生活中的三角形导入,利用这个生活资源弥补课程资源的不足,为我们转变教育教学方式,适应新课程提供有力的支持和保证。
2.如何正确地理解并画出三角形的高是本节课的教学难点。为什么学生在画高的时候经常会出现错误,经过认真分析与思考后,发现学生出现错误的原因在于学生对于三角形的高的意义没有理解到位,他们不能正确地找到顶点及相应的对边,学生的操作是在模仿中进行的。因此,先利用三角形帮助学生找顶点及相应的对边,分散三角形的高定义中的难点,最后让学生通过“猜想”“推理”,感知三角形不同的高及相应的底。
3.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】数一数,下面各图分别有多少个三角形?
图1 图2
图3 图4
你发现了什么规律吗?说说看。
分析:图1有2个小三角形和1个大三角形,一共是2+1=3(个)三角形;图2有3个小三角形,相邻两个小三角形组成2个三角形,有1个大三角形,共有3+2+1=6(个)三角形;图3有4个小三角形,相邻两个小三角形组成3个三角形,相邻3个三角形组成2个三角形,有1个大三角形,共有4+3+2+1=10(个)三角形;图4有5个小三角形,相邻两个小三角形组成4个三角形,相邻3个三角形组成3个三角形,相邻4个小三角形组成2个三角形;有1个大三角形,共有5+4+3+2+1=15(个)三角形。由此得出规律:若图形中的单个小三角形个数为n,则图形中三角形的总个数就是1+2+3+4+5+…+n。
解答:图1共有2+1=3(个)三角形。
图2共有3+2+1=6(个)三角形。
图3共有4+3+2+1=10(个)三角形。
图4共有5+4+3+2+1=15(个)三角形。
由此得出规律:若图形中的单个小三角形个数为n,则图形中三角形的总个数就是1+2+3+4+…+n。
解法归纳:从三角形的一个顶点向对边引若干条线段,将三角形分成了若干个小三角形,若小三角形的个数为n,则三角形的总个数为1+2+3+4+…+n。
相关知识阅读
能干的设计师——小“3”
一天,小“1”带着几个伙伴在路边竖一根电视天线杆。天线杆竖起来以后,总是晃来晃去,他们急得团团转。
恰巧小“3”路过这里,看见了,赶忙过来说:“这又直又高的电视天线杆光这样竖着不稳定,有倒斜的危险。”
“请问,您有什么好办法吗?”小“1”诚恳地问。
小“3”说:“用三根绳子从杆子的上方向三个方向拉下来,拉紧以后把绳头固定在地面上,固定在地面上的三点能成一个三角形,天线杆就不会晃了。”
“好!”小“1”他们很快动手,把绳子拉好。果然,天线杆不晃动了。“真行!”“这个办法真灵!”大家一起高兴地围着小“3”询问这是为什么。小“3”笑着说:“因为三角形有一个特性,叫做三角形的稳定性。你看,木制的房顶,自行车的三角架,还有高压电线架都是三角形,就是利用这个特性。”
“你真是个能干的设计师。”小“1”称赞小“3”说。小“3”不好意思地说:“不,我们各有所长,要相互学习。”
“哈哈,各有所长,各有所长……”大伙会心地笑了。
第2课时 三角形三条边的关系
课时目标导航
教学导航
一、教学内容
三角形三条边的关系。(教材第62页例3、例4)
二、教学目标
1.知道两点间距离的意义,明白两点之间线段最短的道理。
2.通过操作、探索,发现三角形三边之间的关系:三角形任意两边的和大于第三边。
3.掌握判断三条线段能否构成一个三角形的方法,并能解决有关的问题。
4.提高学生逻辑思维能力,以及培养学生“猜测——验证——总结”的学习习惯。
三、重点难点
重点:知道两点间距离的意义,明白两点之间线段最短的道理。
难点:三角形三边之间的关系。
教学过程
一、情境引入
师:这是小明同学上学的路线。请大家仔细观察,他可以怎样走?在这几条路线中哪条最近?为什么?(课件展示教材第62页例3情境图)
师:要明白这些问题,就要学习本节课的内容,你准备好了吗?(课件展示课题:三角形三条边的关系)
二、学习新课
1.教学教材第62页例3——两点间的距离的意义。
师:小明上学走哪条路最近?(课件展示教材第62页例3情境图)
师:观察情境图说一说,从小明家到学校有几条路线?分别是怎么走的?(分组讨论,指名学生回答)
明确:从小明家到学校有3条路可走。
第一条:家→邮局→学校
第二条:家→学校
第三条:家→商店→学校
师:哪条路最近?(指名学生回答)
明确:家→学校这条路最近。
师:为什么大家都认为中间这条路最近?(小组讨论,学生反馈)
理由1:因为第一条和第三条路线拐弯了,绕远路,所以中间这条最近。
理由2:生活中这样走过,中间的这条路线最短。
理由3:在课本的图中通过测量得出中间的这条路线最短。
……
(引导学生积极发言,教师指导理解有困难的学生)
教师指导学生进行测量,从而明确中间这条路最近。
师:家、邮局、学校,我们可以看作三个点,你能发现它们构成了一个什么图形吗?(让学生结合情境图说一说)
明确:观察情境图可以发现家→邮局→学校可以看成一个三角形,其中家到邮局的距离+邮局到学校的距离>家到学校的距离。家→商店→学校也可以看成一个三角形,家到商店的距离+商店到学校的距离>家到学校的距离。
师:通过上面的观察,你能得出什么结论?
师生共同总结:两点之间,线段最短。
教师指导:在数学上,把连接两点间的线段的长度叫做两点间的距离。
2.教学教材第62页例4——三角形三条边的关系。
(课件展示教材第62页例4)
师:剪出下面4组长度的纸条。(单位:cm)。
(1)6、7、8。
(2)4、5、9。
(3)3、6、10。
(4)8、11、11。
师:用每组纸条摆三角形,哪些能摆出三角形?哪些不能摆出三角形?(学生分小组拼摆三角形,小组讨论,全班交流)
通过拼摆发现,上面的四组纸条有的可以摆成三角形,有的不能摆成三角形,能摆成三角形的是(1)和(4),不能摆成三角形的是(2)和(3)。
师:对比能与不能摆成三角形的三根纸条的长度你能发现什么?(分组讨论,集体订正)
不能摆成三角形的三根纸条中,有两根的长度之和等于或小于第三根,如4+5=9,3+6<10;能摆成三角形的三根纸条中,任意两根长度的和都大于第三根的长度,如6+7>8,8+11>11。
师:你能用自己的语言概括一下上面你的发现吗?(指名学生回答)
师生共同总结:三角形任意两边的和大于第三边。
三、巩固反馈
1.下面每组中的三条线段能否围成一个三角形?说明理由。(学生独立完成)
(1)3 cm、7 cm、5 cm
(2)6 cm、2 cm、2 cm
(3)8 cm、4 cm、4 cm
答案:(1)能 3+5>7 (2)不能 2+2<6 (3)不能 4+4=8
2.从长度分别为3 cm、5 cm、8 cm、4 cm的4根小棒中选出3根,围成一个三角形。你准备怎么选?为什么?(学生分组讨论、交流,派代表反馈,说明解题重点)
答案:5 cm、8 cm、4 cm或者是3 cm、4 cm、5 cm。因为三角形任意两边的和大于第三边。
四、课堂小结
1.说一说这堂课的收获。
2.三角形的三边关系是什么?
板书设计
三角形三条边的关系
例3 两点间的距离:两点间的所有连线中线段最短,这条线段的长度叫做两点间的距离。
例4 可以围成三角形的三边 6+7>8 8+11>11
不可以围成三角形的三边 4+5=9 3+6<10
判断标准:较小的两条线段的和大于第三条线段。
发现:三角形的任意两边的和大于第三边。
教学反思
1.本节课通过让学生仔细观察小明上学的路线图,发现连接小明家、商店、学校三地近似是一个三角形,而连接小明家、邮局、学校三地同样也近似是一个三角形。走中间的这条路实际上就是三角形的一条边,走小明家→商店→学校或走小明家→邮局→学校的路程实际上是三角形的另外两条边的和,发现三角形的两条边的和要比第三边大。这就引出了这节课要探究的问题:是不是所有的三角形的三条边都有这样的关系呢?在探究这个问题时,让每个小组用不同的四组纸条来摆三角形,通过操作让学生发现有的三根纸条不能摆成三角形,有的三根纸条却能摆成三角形,而能摆成三角形的三根小棒都有一个共同规律,由此得出三角形任意两边的和大于第三边。
2.我的补充:
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】把一根12厘米的吸管剪成3段(每段都是整厘米数),摆成一个三角形,共有几种剪法,你能全部列举出来吗?
分析:因为三角形任意两边的和大于第三边,且三条边的总长为12厘米,所以摆成的三角形的最长边<6厘米,即最长边最大是5厘米。将12厘米分成三个整厘米数相加且满足三角形任意两边的和大于第三边的形式为12=3+4+5=4+4+4=2+5+5。
符合题意的三角形各边分别为:①3厘米、4厘米、5厘米;②4厘米、4厘米、4厘米;③2厘米、5厘米、5厘米。
解答:共有3种剪法,可以是3厘米、4厘米、5厘米;4厘米、4厘米、4厘米;2厘米、5厘米、5厘米。
解法归纳:先确定最长边最大的取值,再将12分成三个整数相加且满足三角形任意两边的和大于第三边的形式。
相关知识阅读
三角形任意两边的和大于第三边的原理
有A、B两点,连接AB,得到线段AB(如图1),线段AB外有任意一点C,连接AC、BC,组成三角形ABC(如图2)。由“两点间所有连线中线段最短”可知,AB
图1 图2
