三年级数学下册教案-第8单元 1数学广角——搭配(二)-人教版
文档属性
| 名称 | 三年级数学下册教案-第8单元 1数学广角——搭配(二)-人教版 |  | |
| 格式 | doc | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 06:00:19 | ||
图片预览




文档简介
1 数学广角——搭配(二)
第1课时 稍复杂的排列
课时目标导航
教学导航
一、教学内容
稍复杂的排列。(教材第101页例1)
二、教学目标
1.通过动手操作找出简单事物的排列数,探索排列的规律。
2.培养学生初步的观察、分析、推理能力,以及有顺序地、全面地思考问题的意识。
3.培养学生对数学的兴趣以及与人合作的良好习惯。
三、重点难点
重难点:简单事物的排列数。
教学过程
一、复习引入
1.十位上是“2”的两位数共有多少个?
2.个位上是“0”的两位数共有多少个?
二、学习新课
教学教材第101页例1。
(课件出示教材第101页例1)
组织学生读题,理解题意,明确是组成两位数,并且不能有重复数字。
强调:0不能在首位,因此,十位上的数字只能是1、3、5这3个数,个位上的数字可以是0、1、3、5这4个数。
师:满足要求的两位数有哪些呢,如何才能把它们全部找出来呢?(小组交流讨论,点名小组代表回答)
引导学生可以按照一定的顺序来组成满足要求的两位数,比如先按从小到大的顺序确定十位上的数字取值,再分别写出此时个位上的数字的可能取值。
师:如果十位上是1,个位上可以取哪些值?(点名学生回答,板书学生答案)
师:如果十位上是3或5呢?(点名学生回答,板书学生答案)
师:通过我们上面的步骤,同学们认为还有考虑遗漏或者重复的两位数吗?(小组交流讨论,点名小组代表回答)
引导学生明确,所有满足条件的两位数都已经列举出来了,没有重复和遗漏。因此,用0、1、3、5这四个数一共能组成9个没有重复数字的两位数。(板书:能组成9个没有重复数字的两位数。)
师:通过上面的解题过程,同学们能归纳总结下解决这类问题时,可以采用什么方法吗?写数时有哪些注意问题呢?(小组交流讨论,点名小组代表回答,教师点评总结)
教师小结:用几个不同数字组成没有重复数字的两位数时,可以按照一定的顺序写,这样能有效避免重复和遗漏。当数字中有0时,注意0不能放于两位数的十位上;当十位上已选择某一个数字时,个位上就不能再用这个数字了。(课件出示小结)
三、巩固反馈
完成教材第101页“做一做”。(点名学生回答,如有遗漏,其余学生补充,引导学生按顺序思考)
第1题:20、24、26、40、42、46、60、62、64,一共9个。
第2题:6种。
四、课堂小结
谈谈在解决排列问题中有哪些需要注意或不太懂的地方?
板书设计
稍复杂的排列
例1:十位如果是1,可以摆出10、13、15;
十位如果是3,可以摆出30、31、35;
十位如果是5,可以摆出50、51、53。
能组成9个没有重复数字的两位数。
教学反思
1.本节课通过“编数字”的情境,激发了学生的探究欲望,各教学环节紧密联系生活实际,体现了数学在生活中的应用价值,使学生在轻松愉快中学习数学。
2.本节课的教学设计是以“活动”为主线,让学生通过自己的观察、操作、探索、交流等形式,经历知识的发生、形成与应用的全过程,更重要的是让学生在活动中探索,充分发挥了学生的主动性。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】用写有0、5、3、8的四张纸片,能组成哪些不同的四位数,把它们写出来。
分析:按照从小到大的顺序把0、5、3、8组成的四位数写出即可,注意最高位上不能是0。
解答:用0、5、3、8组成的四位数有:
3058、3085、3508、3580、3805、3850;
5038、5083、5308、5380、5803、5830;
8035、8053、8305、8350、8503、8530。
一共有18个。
相关知识阅读
乘法原理
如果做某件事,需要分几个步骤才能完成,而每个步骤又有几种不同的方法,那么完成这件事的方法总数就等于完成各步骤方法数的乘积。
例:用1、2、3、4这四个数字可以组成多少个不同的三位数?
要完成组成一个三位数这件事,要分三个步骤做,首先选百位上的数,再选十位上的数,最后选个位上的数。
“选百位上的数”这一步骤中,可选1、2、3、4任何一个,共4种方法。
“选十位上的数”这一步骤中,可选除百位上已选好那个数字之外的另三个数字,共3种方法。
“选个位上的数”这一步骤中,可选除百、十位上已选好的两个数字之外的另两个数字,共2种方法。
所以,可以组成4×3×2=24(个)不同的三位数。
第2课时 搭配问题
课时目标导航
教学导航
一、教学内容
搭配问题。(教材第102页例2)
二、教学目标
1.让学生熟悉更加有难度的搭配问题,学会化具体为抽象,进一步了解搭配的知识。
2.通过图形连线或实物操作的动手过程,让学生体会组合的特点和结果。
3.培养学生观察、分析问题的能力,增强学生合作交流的意识,提高学生解决实际问题的能力。
三、重点难点
重点:理解并掌握组合实物方法。
难点:理解组合可以不分顺序。
教学过程
一、情境引入
同学们,你们喜欢过生日吗?今天是聪聪的生日,她邀请大家去参加她的生日聚会,你们愿意去吗?可是,聪聪遇到了麻烦事,她有一件牛仔上衣、一件T恤;两条裙子、一条裤子,怎样搭配才好呢?她左选右选,还是拿不定主意,同学们你能帮帮聪聪吗?
二、学习新课
教学教材第102页例2。
(课件出示教材第102页例2)
师:哪位同学能来介绍一下聪聪都有几件上装和下装呢?(点名学生回答)
明确聪聪有2件上装,3件下装。
提醒学生注意隐含条件:每次一件上装只能搭配一件下装。
师:你会建议聪聪穿哪套衣服呢?(点名学生回答)
师:聪聪想知道还有哪些衣服搭配方式,同学们能帮她列举出来吗?(小组交流讨论,点名小组代表回答)
引导学生可以将实物抽象为符号或字母,再连线展示。
组织学生动手画一画,教师巡视指导。
教师一边讲解,一边板书:
方法一:用○表示上装,□表示下装,搭配结果如下:
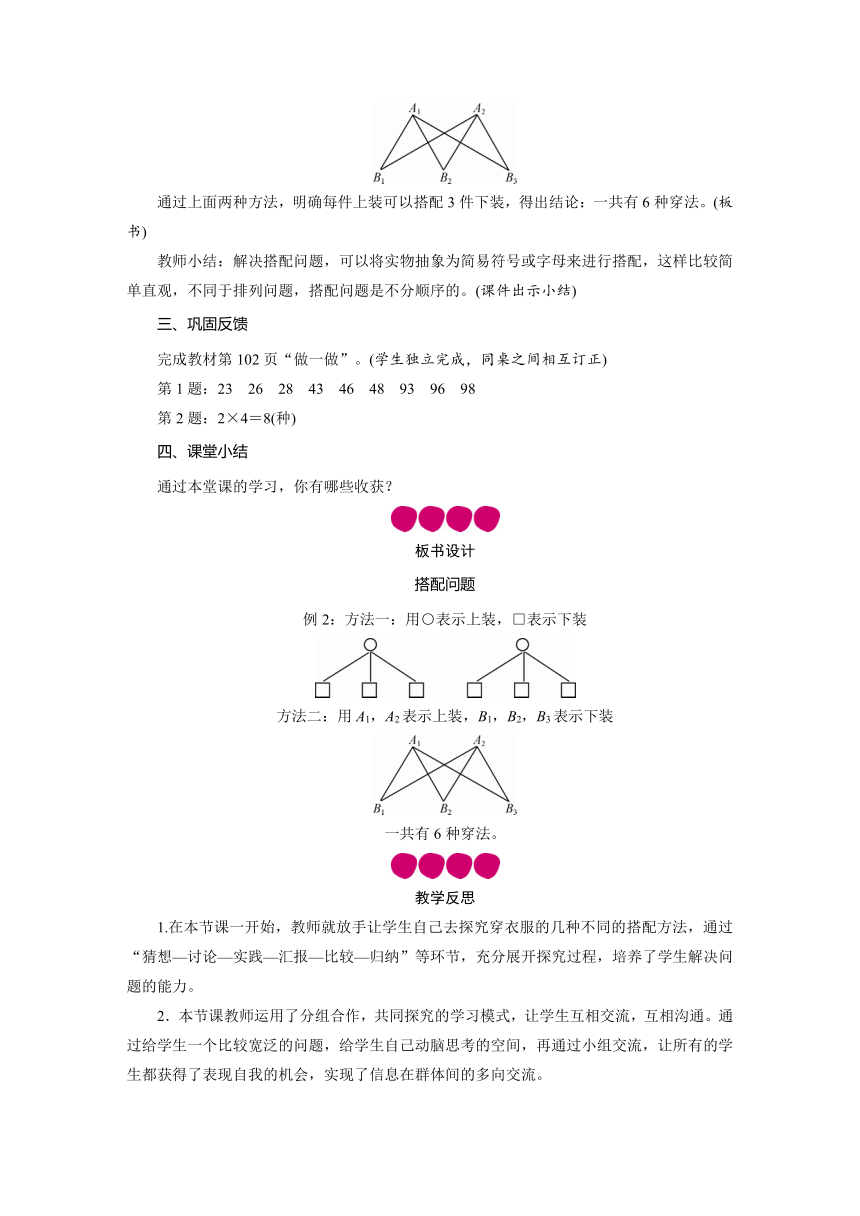
方法二:用A1,A2表示上装,B1,B2,B3表示下装,搭配结果如下:
通过上面两种方法,明确每件上装可以搭配3件下装,得出结论:一共有6种穿法。(板书)
教师小结:解决搭配问题,可以将实物抽象为简易符号或字母来进行搭配,这样比较简单直观,不同于排列问题,搭配问题是不分顺序的。(课件出示小结)
三、巩固反馈
完成教材第102页“做一做”。(学生独立完成,同桌之间相互订正)
第1题:23 26 28 43 46 48 93 96 98
第2题:2×4=8(种)
四、课堂小结
通过本堂课的学习,你有哪些收获?
板书设计
搭配问题
例2:方法一:用○表示上装,□表示下装
方法二:用A1,A2表示上装,B1,B2,B3表示下装
一共有6种穿法。
教学反思
1.在本节课一开始,教师就放手让学生自己去探究穿衣服的几种不同的搭配方法,通过“猜想—讨论—实践—汇报—比较—归纳”等环节,充分展开探究过程,培养了学生解决问题的能力。
2.本节课教师运用了分组合作,共同探究的学习模式,让学生互相交流,互相沟通。通过给学生一个比较宽泛的问题,给学生自己动脑思考的空间,再通过小组交流,让所有的学生都获得了表现自我的机会,实现了信息在群体间的多向交流。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】明明的书架分上、下两层,上层放着2本不同的漫画书,下层放着4本不同的童话书。
(1)明明从书架上任意取出一本书,有几种不同的取法?
(2)明明从上、下层书架上各取一本书,有几种不同的取法?
分析:(1)明明从6本中任选1本,可以是其中的任何一本;(2)从上层的2本中任选1本,有2种选法,从下层的4本中任选1本,有4种选法,它们的积就是全部的选法。
解答:(1)6本中任选1本,共有6种不同的取法。
答:有6种不同的取法。
(2)上层有2种选法,下层有4种选法,
2×4=8(种)
答:有8种不同的取法。
相关知识阅读
天干地支
在中国古代,广泛使用“天干、地支”(简称“干支”),按字面上的意义来说,“干”的原始本义是树干,“支”的本义是树枝。两者关系自然是干为主,支为从。我国古代以天为主,以地为从,从而叫做天干和地支。
天干指甲、乙、丙、丁、戊、己、庚、辛、壬、癸十个字;地支指子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个字。以十天干配十二地支的前十个字,为一轮,然后又从天干的第一字(甲)开始与地支第十一个字(戌)相配,依次轮转。这样天干轮转6次,地支轮转5次,共为60次。这里把十天干的每个字都作为顺序符号来使用,十二地支的每个字也是如此。从3000多年前,天干与地支结对,形成60对有序文字用以标志60个顺序符号,一直流传至今,没有改变。
第3课时 稍复杂的组合
课时目标导航
教学导航
一、教学内容
稍复杂的组合。(教材第103页例3)
二、教学目标
1.通过动手操作,感受到组合数与顺序无关, 会用图示法解决稍复杂的组合问题。
2.通过用不同方法解决组合问题的探究过程,感受解决组合问题策略的多样性。
3.体会数学在现实生活中的广泛应用,并尝试用数学的方法解决生活中的实际问题。
三、重点难点
重点:利用所学知识解决组合问题。
难点:会用不同的方法解决组合问题。
教学过程
一、复习引入
老师有5个颜色不同的气球,将它们分给4个同学,每人一个,总共有多少种分法?
师:上一节课我们学习了搭配问题,这节课我们继续学习稍复杂的组合问题。(板书课题:稍复杂的组合)
二、学习新课
教学教材第103页例3。
(课件出示教材第103页例3)
组织学生读题,理解题意,已知有4个国家的足球队进行比赛,每2个球队踢一场,求一共要踢多少场。
师:这是一个排列问题还是组合问题?(小组交流讨论,点名小组代表回答)
引导学生明确:这是一个组合问题,因为2个球队踢一场之间是没有顺序的,如中国队与乌兹别克斯坦队踢一场和乌兹别克斯坦队与中国队踢一场表示的是同一场。
师:同解决搭配问题一样,我们可以用连线法来解决组合问题。为了使结果直观,我们可以用球队名表示球队,然后将2个球队连线组合。同学们可以先自己试着画一画,并数一数一共有多少种连线方法。
明确:把2个队用一条线连起来,就可以表示这2个队已踢了一场。
组织学生独立画图,教师巡视。
教师一边讲解,一边板书演示:
方法一:4个球队排成正方形,用直线连。
方法二:4个球队依次排开,用曲线连。
师:通过以上两种不同的方法,我们可以知道一共要踢6场。(板书)
教师小结:对于稍复杂的组合问题,可以用画图连线的方法来解决,画了几条线,组合数就是几。画图连线的方法有多种,只要注意按一定的顺序连线,就能做到不重复无遗漏。(课件出示小结)
三、巩固反馈
完成教材第103页的“做一做”。(学生独立完成,教师巡视指导,集体订正)
第1题:10次
第2题:取出的钱共有6种情况,分别是:1元和5分,1元和5角,1元和1角,5角和5分,1角和5分,1角和5角。
四、课堂小结
谈谈在解决稍复杂的组合问题中有哪些需要注意或不太懂的地方?
板书设计
稍复杂的组合
一共要踢6场。
备课资料参考
相关知识阅读
亚洲杯
亚洲杯足球赛是由亚洲足联举办的国际性成年男子足球队比赛,每四年举办一届。亚洲杯是世界上除了美洲杯以外历史最悠久的洲际国家队比赛,比第一届欧锦赛还要早四年创办。亚洲杯也是亚洲地区内最高级别的国家级足球赛事,参赛球队必须是亚洲足联成员。从1997年开始,亚洲杯冠军代表亚洲足联参加国际足联联合会杯。
第4课时 练习课
课时目标导航
教学导航
一、教学内容
稍复杂的排列、组合问题的运用练习。(教材第104~105页练习二十二第2、4、7、8题)
二、教学目标
1.巩固排列、搭配、组合问题的基本解题方法,会求解简单事件的排列、组合数。
2.掌握排列和组合的区别,能正确判断问题属于排列问题还是组合问题。
3.培养学生分析、解决问题的能力,让学生养成有序、全面思考问题的意识和习惯。
三、重点难点
重难点:利用所学知识正确解决排列、组合问题。
教学过程
一、基础练习
1.有3、6、8、0四个数字,能组成多少个没有重复数字的三位数?
2.妈妈去水果店买水果,看到有苹果、梨、香蕉、水蜜桃四种水果。如果妈妈要买其中任意两种水果,一共有多少种买法?
二、指导练习
(课件依次出示各题)
1.教学教材第104页练习二十二第2题。
师:这是一个排列问题还是组合问题?说说你的理由。(点名学生回答)
师:这个两位数的个位数字是单数,那么它能够取哪些数呢?(点名学生回答)
明确这个两位数个位只能取值1、3、5、7、9。因此,用2、5、7、9组成两位数,个位上可以取5、7、9,十位上可以取2、5、7、9,十位上和个位上的数字不重复。
师:那么这个两位数可以取哪些值,一共有多少个呢?(点名学生回答,板书学生答案)
2.教学教材第104页练习二十二第4题。
引导学生画图解决,将明明、聪聪以及四位同学抽象为符号或字母,连线搭配,每一条连线代表合拍一张照片,数一数连了多少条线就表示拍了多少张照片。
点名学生板演,其余学生独立画图解决。
3.教学教材第105页练习二十二第7题。
引导学生明确这是一个组合问题,可以通过连线法画图解决。
点名两位学生板演,分别用排成正方形连直线和依次排开连曲线的方法解决,其余学生独立完成,教师巡视指导。提醒学生按照一定的顺序连线。
4.教学教材第105页练习二十二第8题。
师:问题(1)是排列问题还是组合问题?(点名学生回答)
组织学生用书名表示这四本书,排成正方形或依次排开,画图连线,通过连线得出从4本书中任选2本,一共有6种选法。(点名学生板演)
师:对于问题(2),我们不知道小明选的另外一本书是哪一本,那么如何确定一共有多少种送法呢?(小组交流讨论,点名小组代表回答)
引导学生理解这本其他的书共有3种选法,当把《数学家的故事》送给小红,这本其他的书送给小丽时,有3种送法,把这本其他的书送给小红,《数学家的故事》送给小丽时,也有3种送法,因此一共有6种送法。
教师板书连线展示这6种送法。
师:上面的计算过程有重复或者遗漏吗?(小组交流讨论)
三、巩固练习
完成教材第104~105页“练习二十二”第1、3、6、9题。(学生独立完成,集体订正)
第1题:6种
第3题:18种
第6题:8条
第9题:(1)0.567、0.576、0.657、0.675、0.756、0.765
(2)7.056、7.065、7.506、7.605、7.560、7.650
四、课堂小结
通过本堂课的学习,你有什么收获?
板书设计
练习课
2.能组成25、27、29、57、59、75、79、95、97,共9个。
8.(1)
(2)
教学反思
1.本堂练习课的教学中采用“提出问题—探索问题—互动交流”的教学模式,引导学生掌握排列问题和组合问题的区别,学会将具象问题抽象化,使得解决问题的方法更加简便,为学生的自主学习提供了良好的环境。
2.学生在学习本单元的知识点时主要存在以下问题:(1)有遗漏。(2)有重复。因此,在练习课的教学中,也需要根据学生的课堂反馈情况,对这类问题做出指正,并组织学生交流讨论,如何才能确保不重复、不遗漏。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】往返于南宁和上海之间的沪宁高速列车沿途要停靠常州、无锡、苏州三站,铁路部门要为这趟车准备多少种不同的车票?
分析:我们可以根据列车的往与返把它们分成两大类(注:为了方便,我们将上述地点简称为宁、常、锡、苏、沪):在第一大类中,我们又可以根据乘客乘车时所在起点站的不同分成4类。第1类:从宁出发:宁→常,宁→锡,宁→苏,宁→沪,4种;第2类:从常出发:常→锡,常→苏,常→沪,3种;第3类:从锡出发:锡→苏,锡→沪,2种;第4类:从苏出发:苏→沪,1种。我们同样可用刚才的方法将回来的车票分类,它的种数与第一大类完全相同。
解答:(4+3+2+1)×2=20(种)
答:铁路部门要准备20种不同的车票。
相关知识阅读
加法原理
如果完成某件事共有几类不同的方法,而每类方法中,又有几种不同的方法,任选一种方法都可以完成此事,那么完成这件事的方法总数就等于各种方法的总和,这一原理称为加法原理。
例:从甲地到乙地,一天中火车有4班,汽车有2班,轮船有3班,那么,一天中乘坐这些交通工具从甲地到乙地,共有多少种不同的走法?
把乘坐不同班次的车、船称为不同的走法。要完成从甲地到乙地这件事,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,乘火车有4种走法,乘汽车有2种走法,乘轮船有3种走法。而乘坐火车、汽车、轮船中的任何一班次,都可以从甲地到乙地,所以从甲地到乙地的总的走法=乘火车的4种走法+乘汽车的2种走法+乘轮船的3种走法=9种不同的走法。
第1课时 稍复杂的排列
课时目标导航
教学导航
一、教学内容
稍复杂的排列。(教材第101页例1)
二、教学目标
1.通过动手操作找出简单事物的排列数,探索排列的规律。
2.培养学生初步的观察、分析、推理能力,以及有顺序地、全面地思考问题的意识。
3.培养学生对数学的兴趣以及与人合作的良好习惯。
三、重点难点
重难点:简单事物的排列数。
教学过程
一、复习引入
1.十位上是“2”的两位数共有多少个?
2.个位上是“0”的两位数共有多少个?
二、学习新课
教学教材第101页例1。
(课件出示教材第101页例1)
组织学生读题,理解题意,明确是组成两位数,并且不能有重复数字。
强调:0不能在首位,因此,十位上的数字只能是1、3、5这3个数,个位上的数字可以是0、1、3、5这4个数。
师:满足要求的两位数有哪些呢,如何才能把它们全部找出来呢?(小组交流讨论,点名小组代表回答)
引导学生可以按照一定的顺序来组成满足要求的两位数,比如先按从小到大的顺序确定十位上的数字取值,再分别写出此时个位上的数字的可能取值。
师:如果十位上是1,个位上可以取哪些值?(点名学生回答,板书学生答案)
师:如果十位上是3或5呢?(点名学生回答,板书学生答案)
师:通过我们上面的步骤,同学们认为还有考虑遗漏或者重复的两位数吗?(小组交流讨论,点名小组代表回答)
引导学生明确,所有满足条件的两位数都已经列举出来了,没有重复和遗漏。因此,用0、1、3、5这四个数一共能组成9个没有重复数字的两位数。(板书:能组成9个没有重复数字的两位数。)
师:通过上面的解题过程,同学们能归纳总结下解决这类问题时,可以采用什么方法吗?写数时有哪些注意问题呢?(小组交流讨论,点名小组代表回答,教师点评总结)
教师小结:用几个不同数字组成没有重复数字的两位数时,可以按照一定的顺序写,这样能有效避免重复和遗漏。当数字中有0时,注意0不能放于两位数的十位上;当十位上已选择某一个数字时,个位上就不能再用这个数字了。(课件出示小结)
三、巩固反馈
完成教材第101页“做一做”。(点名学生回答,如有遗漏,其余学生补充,引导学生按顺序思考)
第1题:20、24、26、40、42、46、60、62、64,一共9个。
第2题:6种。
四、课堂小结
谈谈在解决排列问题中有哪些需要注意或不太懂的地方?
板书设计
稍复杂的排列
例1:十位如果是1,可以摆出10、13、15;
十位如果是3,可以摆出30、31、35;
十位如果是5,可以摆出50、51、53。
能组成9个没有重复数字的两位数。
教学反思
1.本节课通过“编数字”的情境,激发了学生的探究欲望,各教学环节紧密联系生活实际,体现了数学在生活中的应用价值,使学生在轻松愉快中学习数学。
2.本节课的教学设计是以“活动”为主线,让学生通过自己的观察、操作、探索、交流等形式,经历知识的发生、形成与应用的全过程,更重要的是让学生在活动中探索,充分发挥了学生的主动性。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】用写有0、5、3、8的四张纸片,能组成哪些不同的四位数,把它们写出来。
分析:按照从小到大的顺序把0、5、3、8组成的四位数写出即可,注意最高位上不能是0。
解答:用0、5、3、8组成的四位数有:
3058、3085、3508、3580、3805、3850;
5038、5083、5308、5380、5803、5830;
8035、8053、8305、8350、8503、8530。
一共有18个。
相关知识阅读
乘法原理
如果做某件事,需要分几个步骤才能完成,而每个步骤又有几种不同的方法,那么完成这件事的方法总数就等于完成各步骤方法数的乘积。
例:用1、2、3、4这四个数字可以组成多少个不同的三位数?
要完成组成一个三位数这件事,要分三个步骤做,首先选百位上的数,再选十位上的数,最后选个位上的数。
“选百位上的数”这一步骤中,可选1、2、3、4任何一个,共4种方法。
“选十位上的数”这一步骤中,可选除百位上已选好那个数字之外的另三个数字,共3种方法。
“选个位上的数”这一步骤中,可选除百、十位上已选好的两个数字之外的另两个数字,共2种方法。
所以,可以组成4×3×2=24(个)不同的三位数。
第2课时 搭配问题
课时目标导航
教学导航
一、教学内容
搭配问题。(教材第102页例2)
二、教学目标
1.让学生熟悉更加有难度的搭配问题,学会化具体为抽象,进一步了解搭配的知识。
2.通过图形连线或实物操作的动手过程,让学生体会组合的特点和结果。
3.培养学生观察、分析问题的能力,增强学生合作交流的意识,提高学生解决实际问题的能力。
三、重点难点
重点:理解并掌握组合实物方法。
难点:理解组合可以不分顺序。
教学过程
一、情境引入
同学们,你们喜欢过生日吗?今天是聪聪的生日,她邀请大家去参加她的生日聚会,你们愿意去吗?可是,聪聪遇到了麻烦事,她有一件牛仔上衣、一件T恤;两条裙子、一条裤子,怎样搭配才好呢?她左选右选,还是拿不定主意,同学们你能帮帮聪聪吗?
二、学习新课
教学教材第102页例2。
(课件出示教材第102页例2)
师:哪位同学能来介绍一下聪聪都有几件上装和下装呢?(点名学生回答)
明确聪聪有2件上装,3件下装。
提醒学生注意隐含条件:每次一件上装只能搭配一件下装。
师:你会建议聪聪穿哪套衣服呢?(点名学生回答)
师:聪聪想知道还有哪些衣服搭配方式,同学们能帮她列举出来吗?(小组交流讨论,点名小组代表回答)
引导学生可以将实物抽象为符号或字母,再连线展示。
组织学生动手画一画,教师巡视指导。
教师一边讲解,一边板书:
方法一:用○表示上装,□表示下装,搭配结果如下:
方法二:用A1,A2表示上装,B1,B2,B3表示下装,搭配结果如下:
通过上面两种方法,明确每件上装可以搭配3件下装,得出结论:一共有6种穿法。(板书)
教师小结:解决搭配问题,可以将实物抽象为简易符号或字母来进行搭配,这样比较简单直观,不同于排列问题,搭配问题是不分顺序的。(课件出示小结)
三、巩固反馈
完成教材第102页“做一做”。(学生独立完成,同桌之间相互订正)
第1题:23 26 28 43 46 48 93 96 98
第2题:2×4=8(种)
四、课堂小结
通过本堂课的学习,你有哪些收获?
板书设计
搭配问题
例2:方法一:用○表示上装,□表示下装
方法二:用A1,A2表示上装,B1,B2,B3表示下装
一共有6种穿法。
教学反思
1.在本节课一开始,教师就放手让学生自己去探究穿衣服的几种不同的搭配方法,通过“猜想—讨论—实践—汇报—比较—归纳”等环节,充分展开探究过程,培养了学生解决问题的能力。
2.本节课教师运用了分组合作,共同探究的学习模式,让学生互相交流,互相沟通。通过给学生一个比较宽泛的问题,给学生自己动脑思考的空间,再通过小组交流,让所有的学生都获得了表现自我的机会,实现了信息在群体间的多向交流。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】明明的书架分上、下两层,上层放着2本不同的漫画书,下层放着4本不同的童话书。
(1)明明从书架上任意取出一本书,有几种不同的取法?
(2)明明从上、下层书架上各取一本书,有几种不同的取法?
分析:(1)明明从6本中任选1本,可以是其中的任何一本;(2)从上层的2本中任选1本,有2种选法,从下层的4本中任选1本,有4种选法,它们的积就是全部的选法。
解答:(1)6本中任选1本,共有6种不同的取法。
答:有6种不同的取法。
(2)上层有2种选法,下层有4种选法,
2×4=8(种)
答:有8种不同的取法。
相关知识阅读
天干地支
在中国古代,广泛使用“天干、地支”(简称“干支”),按字面上的意义来说,“干”的原始本义是树干,“支”的本义是树枝。两者关系自然是干为主,支为从。我国古代以天为主,以地为从,从而叫做天干和地支。
天干指甲、乙、丙、丁、戊、己、庚、辛、壬、癸十个字;地支指子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个字。以十天干配十二地支的前十个字,为一轮,然后又从天干的第一字(甲)开始与地支第十一个字(戌)相配,依次轮转。这样天干轮转6次,地支轮转5次,共为60次。这里把十天干的每个字都作为顺序符号来使用,十二地支的每个字也是如此。从3000多年前,天干与地支结对,形成60对有序文字用以标志60个顺序符号,一直流传至今,没有改变。
第3课时 稍复杂的组合
课时目标导航
教学导航
一、教学内容
稍复杂的组合。(教材第103页例3)
二、教学目标
1.通过动手操作,感受到组合数与顺序无关, 会用图示法解决稍复杂的组合问题。
2.通过用不同方法解决组合问题的探究过程,感受解决组合问题策略的多样性。
3.体会数学在现实生活中的广泛应用,并尝试用数学的方法解决生活中的实际问题。
三、重点难点
重点:利用所学知识解决组合问题。
难点:会用不同的方法解决组合问题。
教学过程
一、复习引入
老师有5个颜色不同的气球,将它们分给4个同学,每人一个,总共有多少种分法?
师:上一节课我们学习了搭配问题,这节课我们继续学习稍复杂的组合问题。(板书课题:稍复杂的组合)
二、学习新课
教学教材第103页例3。
(课件出示教材第103页例3)
组织学生读题,理解题意,已知有4个国家的足球队进行比赛,每2个球队踢一场,求一共要踢多少场。
师:这是一个排列问题还是组合问题?(小组交流讨论,点名小组代表回答)
引导学生明确:这是一个组合问题,因为2个球队踢一场之间是没有顺序的,如中国队与乌兹别克斯坦队踢一场和乌兹别克斯坦队与中国队踢一场表示的是同一场。
师:同解决搭配问题一样,我们可以用连线法来解决组合问题。为了使结果直观,我们可以用球队名表示球队,然后将2个球队连线组合。同学们可以先自己试着画一画,并数一数一共有多少种连线方法。
明确:把2个队用一条线连起来,就可以表示这2个队已踢了一场。
组织学生独立画图,教师巡视。
教师一边讲解,一边板书演示:
方法一:4个球队排成正方形,用直线连。
方法二:4个球队依次排开,用曲线连。
师:通过以上两种不同的方法,我们可以知道一共要踢6场。(板书)
教师小结:对于稍复杂的组合问题,可以用画图连线的方法来解决,画了几条线,组合数就是几。画图连线的方法有多种,只要注意按一定的顺序连线,就能做到不重复无遗漏。(课件出示小结)
三、巩固反馈
完成教材第103页的“做一做”。(学生独立完成,教师巡视指导,集体订正)
第1题:10次
第2题:取出的钱共有6种情况,分别是:1元和5分,1元和5角,1元和1角,5角和5分,1角和5分,1角和5角。
四、课堂小结
谈谈在解决稍复杂的组合问题中有哪些需要注意或不太懂的地方?
板书设计
稍复杂的组合
一共要踢6场。
备课资料参考
相关知识阅读
亚洲杯
亚洲杯足球赛是由亚洲足联举办的国际性成年男子足球队比赛,每四年举办一届。亚洲杯是世界上除了美洲杯以外历史最悠久的洲际国家队比赛,比第一届欧锦赛还要早四年创办。亚洲杯也是亚洲地区内最高级别的国家级足球赛事,参赛球队必须是亚洲足联成员。从1997年开始,亚洲杯冠军代表亚洲足联参加国际足联联合会杯。
第4课时 练习课
课时目标导航
教学导航
一、教学内容
稍复杂的排列、组合问题的运用练习。(教材第104~105页练习二十二第2、4、7、8题)
二、教学目标
1.巩固排列、搭配、组合问题的基本解题方法,会求解简单事件的排列、组合数。
2.掌握排列和组合的区别,能正确判断问题属于排列问题还是组合问题。
3.培养学生分析、解决问题的能力,让学生养成有序、全面思考问题的意识和习惯。
三、重点难点
重难点:利用所学知识正确解决排列、组合问题。
教学过程
一、基础练习
1.有3、6、8、0四个数字,能组成多少个没有重复数字的三位数?
2.妈妈去水果店买水果,看到有苹果、梨、香蕉、水蜜桃四种水果。如果妈妈要买其中任意两种水果,一共有多少种买法?
二、指导练习
(课件依次出示各题)
1.教学教材第104页练习二十二第2题。
师:这是一个排列问题还是组合问题?说说你的理由。(点名学生回答)
师:这个两位数的个位数字是单数,那么它能够取哪些数呢?(点名学生回答)
明确这个两位数个位只能取值1、3、5、7、9。因此,用2、5、7、9组成两位数,个位上可以取5、7、9,十位上可以取2、5、7、9,十位上和个位上的数字不重复。
师:那么这个两位数可以取哪些值,一共有多少个呢?(点名学生回答,板书学生答案)
2.教学教材第104页练习二十二第4题。
引导学生画图解决,将明明、聪聪以及四位同学抽象为符号或字母,连线搭配,每一条连线代表合拍一张照片,数一数连了多少条线就表示拍了多少张照片。
点名学生板演,其余学生独立画图解决。
3.教学教材第105页练习二十二第7题。
引导学生明确这是一个组合问题,可以通过连线法画图解决。
点名两位学生板演,分别用排成正方形连直线和依次排开连曲线的方法解决,其余学生独立完成,教师巡视指导。提醒学生按照一定的顺序连线。
4.教学教材第105页练习二十二第8题。
师:问题(1)是排列问题还是组合问题?(点名学生回答)
组织学生用书名表示这四本书,排成正方形或依次排开,画图连线,通过连线得出从4本书中任选2本,一共有6种选法。(点名学生板演)
师:对于问题(2),我们不知道小明选的另外一本书是哪一本,那么如何确定一共有多少种送法呢?(小组交流讨论,点名小组代表回答)
引导学生理解这本其他的书共有3种选法,当把《数学家的故事》送给小红,这本其他的书送给小丽时,有3种送法,把这本其他的书送给小红,《数学家的故事》送给小丽时,也有3种送法,因此一共有6种送法。
教师板书连线展示这6种送法。
师:上面的计算过程有重复或者遗漏吗?(小组交流讨论)
三、巩固练习
完成教材第104~105页“练习二十二”第1、3、6、9题。(学生独立完成,集体订正)
第1题:6种
第3题:18种
第6题:8条
第9题:(1)0.567、0.576、0.657、0.675、0.756、0.765
(2)7.056、7.065、7.506、7.605、7.560、7.650
四、课堂小结
通过本堂课的学习,你有什么收获?
板书设计
练习课
2.能组成25、27、29、57、59、75、79、95、97,共9个。
8.(1)
(2)
教学反思
1.本堂练习课的教学中采用“提出问题—探索问题—互动交流”的教学模式,引导学生掌握排列问题和组合问题的区别,学会将具象问题抽象化,使得解决问题的方法更加简便,为学生的自主学习提供了良好的环境。
2.学生在学习本单元的知识点时主要存在以下问题:(1)有遗漏。(2)有重复。因此,在练习课的教学中,也需要根据学生的课堂反馈情况,对这类问题做出指正,并组织学生交流讨论,如何才能确保不重复、不遗漏。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】往返于南宁和上海之间的沪宁高速列车沿途要停靠常州、无锡、苏州三站,铁路部门要为这趟车准备多少种不同的车票?
分析:我们可以根据列车的往与返把它们分成两大类(注:为了方便,我们将上述地点简称为宁、常、锡、苏、沪):在第一大类中,我们又可以根据乘客乘车时所在起点站的不同分成4类。第1类:从宁出发:宁→常,宁→锡,宁→苏,宁→沪,4种;第2类:从常出发:常→锡,常→苏,常→沪,3种;第3类:从锡出发:锡→苏,锡→沪,2种;第4类:从苏出发:苏→沪,1种。我们同样可用刚才的方法将回来的车票分类,它的种数与第一大类完全相同。
解答:(4+3+2+1)×2=20(种)
答:铁路部门要准备20种不同的车票。
相关知识阅读
加法原理
如果完成某件事共有几类不同的方法,而每类方法中,又有几种不同的方法,任选一种方法都可以完成此事,那么完成这件事的方法总数就等于各种方法的总和,这一原理称为加法原理。
例:从甲地到乙地,一天中火车有4班,汽车有2班,轮船有3班,那么,一天中乘坐这些交通工具从甲地到乙地,共有多少种不同的走法?
把乘坐不同班次的车、船称为不同的走法。要完成从甲地到乙地这件事,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,乘火车有4种走法,乘汽车有2种走法,乘轮船有3种走法。而乘坐火车、汽车、轮船中的任何一班次,都可以从甲地到乙地,所以从甲地到乙地的总的走法=乘火车的4种走法+乘汽车的2种走法+乘轮船的3种走法=9种不同的走法。
