三年级数学下册教案-第2单元 2笔算除法-人教版
文档属性
| 名称 | 三年级数学下册教案-第2单元 2笔算除法-人教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 669.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 06:11:43 | ||
图片预览




文档简介
2 笔算除法
第1课时 两位数除以一位数的笔算
课时目标导航
教学导航
一、教学内容
两位数除以一位数的笔算。(教材第15~16页例1、例2)
二、教学目标
1.使学生在理解算理的基础上初步掌握一位数除两位数,商是两位数的计算方法。
2.培养学生观察、分析、推理、概括的能力。
3.掌握除法竖式的书写格式,培养学生认真审题的习惯。
三、重点难点
重点:掌握一位数除两位数的笔算方法,能正确计算一位数除两位数。
难点:掌握一位数除两位数,商是两位数的笔算过程中的试商方法。
四、教学准备
教师准备:课件PPT、小棒。
学生准备:小棒。
教学过程
一、情境引入
师:同学们,你们知道植树节是哪一天吗?(学生齐答)
师:对,就是3月12日。每年的3月12日是植树节,这天人们都会去植树。今年的植树节,三年级和四年级的同学们也去植树了,我们一起去看看吧!(课件出示教材第15页例1情境图)
师:从图中你知道了哪些信息?你能提出哪些问题?(点名学生回答)
组织学生观察情境图,使学生明确:三年级两个班共要种树42棵,四年级两个班共要种树52棵。
师:知道了两个班要种树的总数,我们就可以求平均每班要种多少棵树。
师:我们已经学习了商是一位数的笔算除法,商是两位数的口算除法,那么用两位数除以一位数的笔算,又该怎样计算呢?今天这节课,我们就来学习这部分内容。(板书课题:两位数除以一位数的笔算)
二、学习新课
1.教学教材第15页例1。
(1)师:要求三年级平均每班种多少棵树,应怎样列式?(点名学生回答,教师板书)
师:42÷2还能够利用我们前面所学的口算方法计算吗?你是怎样想的?(点名学生回答)
(2)组织学生汇报。
(3)组织学生以小组为单位,动手分一分。
取4捆小棒(40根)和2根散棒,一共42根,把这些小棒平均分成2份。让学生在小组中交流讨论,应该怎样分。
师:我们可以先把4捆小棒分成2份,每份2捆,也就是先用4个十除以2,得到2个十;再把2根散棒分成2份,每份1根,也就是用2个一除以2,得到1个一,合起来就是21根。(教师演示分小棒过程,课件出示分小棒图)
师:21就是42÷2的商,求得的商是两位数,以前我们学习了商是一位数的笔算除法,现在出现了商是两位数的除法,根据刚才分小棒的过程,同学们会不会列竖式笔算呢?(学生独立完成,教师巡视指导)
板书下面的竖式,教师讲解算理,明确书写要求。
师:因为我们在分小棒时,是先分整捆的,所以在竖式计算中就要先分十位上的数。在42中,4在十位上,我们从整十数除起,4个十除以2,应该得2个十,2个十要写在十位“4”的上面。再用2个十乘2,应该得4个十,这个4应该写在被除数十位“4”的下面,表示从被除数中分掉的数是40,为了简便,0可以省略不写,再用4减4得0。表示被除数中的整十数正好分完。接着我们再求商的个位,从图上看,分完了整捆的,还有2根没有分,从竖式看十位数正好分完,还有个位上的2没有分。我们继续求商的个位,在竖式中把个位上的2落下来,用求商的十位的方法来求出商的个位。2个一除以2,得1个一,商1写在被除数个位“2”的上面。得出42÷2的商是21。
(4)师生共同小结。
笔算两位数除以一位数,当十位可被整除时,先用一位数去除被除数十位上的数,商写在十位的上面,再用一位数去除个位上的数,商写在个位的上面。(课件出示小结)
2.教学教材第16页例2。
(1)师:要求四年级平均每班种多少棵,应怎样列式?(点名学生回答,教师板书)
(2)组织学生动手分小棒,用分小棒的方法求解这个问题。
师:你在分小棒的过程中遇到了什么问题吗?(点名学生回答)
师:52÷2也就是把52根小棒(5捆和2根)平均分成2份。先把5捆平均分成2份,每份是2捆(20根),还余1捆。这1捆应该怎么分呢?(小组交流讨论)
师:对了,我们可以把剩下的1捆(10根)拆开,与2根合起来是12根,再把12根平均分成2份,每份是6根,加起来共分得26根,所以52÷2=26。(教师演示分小棒过程,课件出示分小棒图)
(3)引导学生将分小棒求解的过程写成除法竖式的形式。(学生独立完成,教师巡视指导)
板书下面的竖式,教师讲解算理,明确书写要求。
(4)师生共同小结。
笔算两位数除以一位数,当十位不可被整除时,先用一位数除被除数十位上的数,把余数和个位上的数合并,再用除数去除,除到被除数的哪一位,就把商写在哪一位的上面。(课件出示小结)
(5)师:这个除法竖式计算过程比较复杂,怎么知道我们的计算结果是否正确呢?你有什么好的建议吗?(引导学生提出验算)
师:不错,为了检验较复杂的除法的计算结果是否正确,我们可以进行验算。在没有余数的除法中,如果“除数×商=被除数”,那么说明原来的除法计算正确,否则计算不正确,需要重新计算。(点名学生板演,检验计算结果的正确性)
3.比较例1和例2的异同点。
引导学生观察比较例1和例2笔算竖式的异同,组织学生互相交流,再点名汇报,集体补充。
相同点:都是从被除数十位上的数除起,除到被除数的哪一位,商就写在哪一位的上面。
不同点:例2的被除数十位上除后还有余数,要与个位上的数合起来再除。
三、巩固反馈
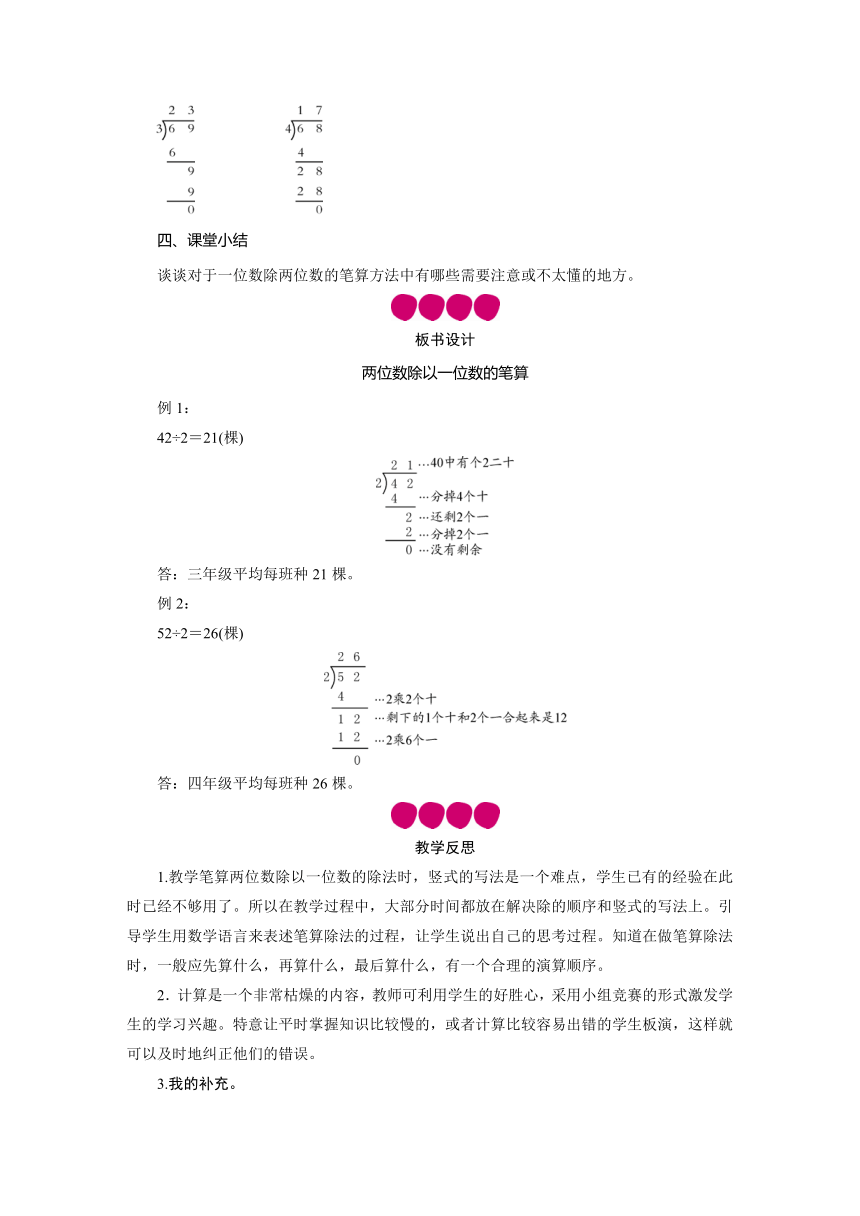
1.完成教材第16页“做一做”。(点名学生板演,其余学生独立完成,集体订正)
32 34 12 23 39 17
2.完成教材第19页“练习四”第1、2题。(点名学生板演第1题;点名学生指出第2题计算错误的笔算竖式,说明错误原因并板演改正)
第1题:13 31 22 11
17 25 14 14
第2题:第二个和第三个计算错误。改正如下:
四、课堂小结
谈谈对于一位数除两位数的笔算方法中有哪些需要注意或不太懂的地方。
板书设计
两位数除以一位数的笔算
例1:
42÷2=21(棵)
答:三年级平均每班种21棵。
例2:
52÷2=26(棵)
答:四年级平均每班种26棵。
教学反思
1.教学笔算两位数除以一位数的除法时,竖式的写法是一个难点,学生已有的经验在此时已经不够用了。所以在教学过程中,大部分时间都放在解决除的顺序和竖式的写法上。引导学生用数学语言来表述笔算除法的过程,让学生说出自己的思考过程。知道在做笔算除法时,一般应先算什么,再算什么,最后算什么,有一个合理的演算顺序。
2.计算是一个非常枯燥的内容,教师可利用学生的好胜心,采用小组竞赛的形式激发学生的学习兴趣。特意让平时掌握知识比较慢的,或者计算比较容易出错的学生板演,这样就可以及时地纠正他们的错误。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】某办公楼前安装了一排彩灯,按照4红,1黄,3绿的顺序排列,第88盏彩灯是什么颜色的?
分析:彩灯以(4+1+3)盏为一个周期不断重复排列,要想知道第88盏彩灯是什么颜色的,就要计算88盏彩灯里包含多少个这样的周期。如果正好是整数周期,说明第88盏彩灯的颜色正好是一个周期中最后一盏彩灯的颜色;如果有余数,余数是几,第88盏彩灯的颜色就是一个周期中第几盏彩灯的颜色。
解答:4+1+3=8(盏)
88÷8=11(个)
答:第88盏彩灯是绿色的。
解法归纳:此题属于周期问题,找到彩灯的排列规律是解此题的关键。
相关知识阅读
植树节
植树节是一些国家法律规定的以宣传保护森林,并动员群众参加以植树造林为活动内容的节日。按时间长短可分为植树日、植树周或植树月,总称植树节。通过这种活动,激发人们爱林、造林的热情,提高人们爱护森林的意识,促进国土绿化,达到爱林护林、扩大森林资源和改善生态环境的目的。植树节是为了动员全民植树而规定的节日。1979年2月23日,中华人民共和国第五届全国人大常务委员会第六次会议决定,以3月12日为中国的植树节,以鼓励全国各族人民植树造林,绿化祖国,改善环境,造福子孙后代。
第2课时 三位数除以一位数的笔算
课时目标导航
教学导航
一、教学内容
三位数除以一位数的笔算。(教材第17~18页例3、例4)
二、教学目标
1.使学生掌握三位数除以一位数的笔算方法。
2.培养学生的验算意识。
3.培养学生认真计算的好习惯。
三、重点难点
重点:掌握三位数除以一位数的笔算方法,运用乘法验算除法。
难点:理解三位数除以一位数的算理。
教学过程
一、复习引入
1.口算。
24÷6= 52÷2= 70÷5=
42÷3= 64÷4= 68÷4=
2.笔算。
36÷3= 36÷2= 78÷3=
师:前面我们学习了两位数除以一位数的口算和笔算,那么,三位数除以一位数又该怎样计算呢?通过本节课的学习,相信同学们就能掌握方法。(板书课题:三位数除以一位数的笔算)
二、学习新课
1.教学教材第17页例3。
(课件出示教材第17页例3)
(1)创设情境,引出问题。
师:小梦和小欣是一对好姐妹,她们经常一起玩耍。今天,两人商量着拿出各自的照片,放在相册里。你们看,她们多认真啊!
组织学生观察情境图,说说从中可以知道哪些信息。(点名学生回答)
引导学生说出:小梦和小欣一共有256张照片,用2本这样的相册正好插完。
师:把256张照片插入2本相册中,求每本相册插多少张照片,应该如何列式呢?(点名学生回答,教师板书)
根据学生的回答教师板书:256÷2=________。
(2)尝试计算,探究新知。
师:你觉得今天学习的三位数除以一位数的计算和上节课学习的两位数除以一位数的计算有什么联系?(小组交流讨论,点名小组代表回答)
师:你能用以前学过的方法计算这道题吗?(引导学生尝试用笔算的方法计算)
教师讲解三位数除以一位数的算理并板书竖式计算过程。
师:三位数除以一位数的算理与两位数除以一位数的算理相同。笔算时,先用2去除被除数的首位,商1,将1写在商的百位上;将求得的商“1”与除数“2”相乘,得到2个百,将“2”写在被除数的百位下面,2减2等于0(0可以省略不写),表示被除数百位上的数已经被分完。接着,将被除数十位上的数“5”写下来,用2去除5,商2,将2写在商的十位上,2与除数“2”相乘得4,将4写在5下面,5减4得1,将1写在4的下面,再将被除数个位上的数“6”写下来,6与十位上的数合成“16”,2除16商8,将8写在商的个位上,8与除数“2”相乘得16,16减16等于0,将0写在余数的位置上。
(3)组织学生验算,检查计算结果是否正确。(点名学生板演验算过程,其他学生独立验算)
2.教学教材第18页例4。
(课件出示教材第18页例4)
(1)组织学生读题,理解题意,说一说从题中获得了哪些信息,问题是什么。(点名学生回答)
引导学生明确:要求可插满多少页,还剩多少张照片用除法计算,除得的商就是页数,余数就是张数。
学生列出算式,教师板书:256÷6=_________(页)……________(张)。
(2)师:大家用竖式算一算,看看计算过程与例3中的三位数除以一位数有什么不同。(小组交流讨论,点名小组代表回答)
师:相信同学们都发现了,例3中的竖式,商是一个三位数,能够整除,而例4中的竖式,商是两位数,有余数。
教师一边板书一边讲解笔算方法。
师:写出竖式,先用被除数256百位上的2除以6,不够商1,再看被除数的前两位,2个百和5个十合起来是25个十,用25个十除以6,商4写在十位的上面,分掉了24个十,余下1个十。余下的1个十和个位上的6个一合起来是16个一,继续除以6,商2写在个位的上面,余数4比除数小。
提醒学生注意:计算除法时,如果除到被除数的个位,仍不能恰好除完,可以留有余数,但余数必须比除数小。
(3)师:对于有余数的除法,我们应该如何验算呢?(点名学生回答)
师:计算结束后,要验算我们的计算是否正确,根据“被除数=除数×商+余数”,我们可以计算42×6+4,看结果是否与被除数相等。(学生独立计算,教师板书验算过程)
验算:
教师强调验算的重要性,让学生养成计算后验算的习惯。
(4)师:通过上面两道例题,你能总结出三位数除以一位数的笔算方法吗?(小组交流讨论,点名小组代表回答)
教师小结:三位数除以一位数,先用除数去除被除数百位上的数,除得的商写在百位的上面;如果被除数百位上的数小于除数,就看被除数的前两位,商的最高位写在十位的上面。除到被除数的哪一位,就把商写在哪一位的上面。每次除得的余数都要比除数小。(课件出示小结)
三、巩固反馈
1.完成教材第17页“做一做”。(点名学生板演,其余学生独立完成,集体订正)
216 174 171 159(竖式,验算略)
2.完成教材第18页“做一做”。(点名学生回答每个竖式的商是几位数,说一说自己的判断理由,再点名学生板演,集体订正)
商是两位数的有:
商是三位数的有:
81……3 61 141……2 51……2(竖式,验算略)
四、课堂小结
对于三位数除以一位数的笔算方法还有哪些疑问?
板书设计
三位数除以一位数的笔算
例3:
256÷2=128(张)
答:每本相册插128张照片。
例4:
256÷6=42(页)……4(张)
答:可插满42页,还剩4张。
教学反思
1.本节课在教学中始终联系学生的生活实际,体现了数学与生活的密切联系。让学生合作学习、互相交流,不仅拓宽了学生的思维,还让每个学生都有了表达自己见解的机会,也培养了学生倾听的习惯。
2.好的评价在一定程度上能激励学生的学习,在本节课中,教师注重对学生的评价。及时对学生的发现进行肯定和表扬,不仅对发言者是一个激励,对其他学生而言,也是非常好的鼓励和鞭策。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】植树节到了,四、五年级的学生参加了义务植树活动,劳动结束时他们共植树129棵,五年级植树的棵数是四年级的2倍。四、五年级各植树多少棵?
分析:因为五年级植树的棵数是四年级的2倍,所以四、五年级学生共植树的129棵是四年级植树棵数的3倍,用四、五年级学生共植树的总棵数除以3即可得四年级植树的棵数,再求五年级植树的棵数即可。
解答:2+1=3
四年级:129÷3=43(棵)
五年级:43×2=86(棵)
答:四年级植树43棵,五年级植树86棵。
相关知识阅读
整除与除尽
整除与除尽既有区别又有联系。除尽是指数a除以数b(b≠0)所得的商是整数或有限小数而余数是0的情况,这时我们就说a能被b除尽(或说b能除尽a)。而只有当被除数、除数以及商都是整数,余数是0时,才能叫整除。也就是说,除尽并不局限于在整数范围内,只要余数是0就可以了。整除是除尽的特殊情况。
第3课时 练习课
课时目标导航
教学导航
一、教学内容
两位数、三位数除以一位数的运用练习。(教材第19~21页练习四第3、6、8、14题)
二、教学目标
1.巩固笔算除法中多位数除以一位数的计算方法及余数的处理方法。
2.通过练习,使学生进一步掌握笔算除法的相关规律,提高计算的效率。
3.在练习的过程中培养学生积极的参与态度和良好的学习习惯。
三、重点难点
重点:掌握笔算除法中的相关运算法则。
难点:提高运算的效率并能熟练运用笔算除法。
教学过程
一、基础练习
笔算。
46÷2= 96÷3= 48÷4=
126÷3= 224÷4= 336÷8=
129÷2= 250÷4= 199÷7=
引导学生根据被除数和除数的特点,判断商是几位数,同桌间相互说一说。
组织学生自主计算,然后互相交流算法,订正计算过程和结果。
二、指导练习
(课件依次出示各题)
1.教学教材第19页练习四第3题。
(1)引导学生看图,理解题意,用自己的语言描述已知条件及所求问题。(点名学生回答,教师板书问题)
问题1:小芳能摆多少组?
问题2:小东能摆多少组?
(2)师:按照小芳的摆法,求能摆多少组,应该如何列式计算?(点名学生回答)
组织学生独立计算,教师巡视,对学生竖式书写的规范性和计算过程进行指导。
引导学生通过验算来保证计算结果的正确性。
根据学生计算结果板书:96÷6=16(组)。
(3)按照上面同样的步骤组织学生列出算式、笔算、验算,求解问题2。
根据学生计算结果板书:96÷8=12(组)。
(4)师:这道题属于两位数除以一位数的笔算问题,同学们能说一说两位数除以一位数的笔算方法吗?(点名学生回答,教师点评总结)
师生共同小结:笔算两位数除以一位数,先用一位数除被除数十位上的数,如果有余数,就把余数和个位上的数合起来,再用除数去除,除到被除数的哪一位,就把商写在哪一位的上面。(课件出示小结)
2.教学教材第20页练习四第6题。
(1)师:我们可以先笔算,再判断商是两位数还是三位数,不过运算量比较大,同学们还能想出更好的办法吗?(小组交流讨论)
师:如果商是三位数,那么用一位数去除三位数时,一位数和被除数的最高位有什么大小关系?(点名学生回答)
引导学生明确:如果被除数最高位上的数字大于或等于除数,那么商就是三位数;否则,商就是两位数。因此可以通过比较被除数最高位上的数字和除数的大小来判断商的位数。
(2)组织学生用上面的方法判断四个除法算式的商的位数,并按要求涂色,完成后集体订正。
3.教学教材第20页练习四第8题。
(1)引导学生看图,理解题意,用自己的语言描述已知条件及所求问题。(点名学生回答)
师:求一个足球多少钱,应该如何列式?(点名学生回答)
组织学生独立笔算出结果,进行验算,教师巡视指导。
根据学生计算结果板书:272÷4=68(元)。
(2)师:你能说一说三位数除以一位数的笔算方法吗?(点名学生回答,教师点评总结)
教师小结:三位数除以一位数,先用除数去除被除数百位上的数,除得的商写在百位的上面,如果被除数百位上的数小于除数,就看被除数的前两位,商的最高位写在十位的上面。除到被除数的哪一位,商就写在哪一位的上面。每次除得的余数都要比除数小。(课件出示小结)
4.教学教材第21页练习四第14题。
(1)组织学生看图,明确已知条件和所求问题。
已知:阿姨带了100元,铅笔单价8元/盒。
问题:求最多可以买多少盒铅笔,还剩多少钱?
师:求最多可以买多少盒铅笔,还剩多少钱,应该怎样计算?
引导学生列出算式:100÷8=________(盒)……________(元)。
师:100除以8的商是几,就可以买几盒铅笔,余数是多少,就还剩多少钱。
组织学生独立计算,集体订正。
根据学生计算结果板书:100÷8=12(盒)……4(元)。
(2)师:像这样的有余数的除法应用题也是我们需要掌握的重点。首先我们需要判断是否该用除法算式解决问题,其次,要明白除法算式的商和余数与问题中的待求量的关系。
三、巩固练习
完成教材第19~22页“练习四”第4、5、10、13、18题。(学生独立完成,集体订正)
第4题:90÷2=45(张)
45÷3=15(张)
第5题:139 185 83 44(竖式、验算略)
第10题:
第13题:336÷8=42(分钟)
第18题:643÷5=128(盆)……3(盆)
四、课堂小结
通过本堂课的学习,你有什么收获?
板书设计
练习课
3.问题1:小芳能摆多少组? 问题2:小东能摆多少组?
96÷6=16(组) 96÷8=12(组)
答:小芳能摆16组。 答:小东能摆12组。
8.272÷4=68(元)
14.100÷8=12(盒)……4(元)
答:最多可以买12盒铅笔,还剩4元。
教学反思
1.本节练习课设计了多层次、多类型的练习,通过对不同类型题目的讲解和练习,使学生熟练掌握各种类型的笔算除法技巧和相关延伸运算方法。既包括对两位数、三位数除以一位数笔算方法的回顾,也包括三位数除以一位数的商的位数的判断的简单技巧介绍,还包括有余数除法的简单实际问题的讲解,通过丰富的练习,提高学生对笔算除法的运用能力。
2.针对不同类型的题目可以设计不同的练习形式。两、三位数除以一位数的笔算倡导学生自主计算,小组相互检查,订正计算过程和结果,再对计算方法进行总结。有关笔算除法的应用题,可以让学生结合条件和问题说一说,提高学生的理解能力,渗透具体问题具体分析的思想。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一道除法算式,小明一时马虎,计算时把除数6看成了9,结果得32余8。正确的得数是多少?
分析:由题意,可知
对比两个算式发现,被除数是不变的。从错误的算式入手,根据“被除数=商×除数+余数”算出被除数=32×9+8=296,再用被除数除以正确的除数,就能算出正确的结果。
解答:32×9+8=296
296÷6=49……2
答:正确的得数是49余2。
解法归纳:解决此类问题时,应该抓住被除数这一不变量,利用“商×除数+余数=被除数”先求出被除数,再进行计算。
第4课时 商中间有0的笔算除法
课时目标导航
教学导航
一、教学内容
商中间有0的笔算除法。(教材第23~24页例5、例6)
二、教学目标
1.使学生知道0除以任何不是0的数都得0。
2.掌握一位数除三位数,商中间有0的除法的算理,会正确计算商中间有0的除法。
3.培养学生良好的计算习惯。
三、重点难点
重点:掌握商中间有0的除法的笔算方法,并能正确进行计算。
难点:理解0在商中的占位作用,能熟练地进行笔算并解决问题。
教学过程
一、复习引入
1.口算练习。
28÷2= 66÷6= 330÷3=
33-4= 0×2= 140÷2=
8×0= 540÷6= 28+0=
6×0=
师:0×2、8×0、6×0这三道题的得数是多少?
2.说一说。
(1)请学生说出数字39中3和9各表示的意义。
(2)请学生说出0表示的意义。
(3)在3和9的中间添上一个0,使39变成“309”,请学生说出0在这个位置表示的意义。
师:0÷8的结果是多少?309除以3又该怎样计算?我们就从这里开始我们今天的课程。(板书课题:商中间有0的笔算除法)
二、学习新课
1.教学教材第23页例5。
(课件出示教材第23页例5)
(1)师:你知道0除以5等于几吗?
引导学生想乘法求除法算式的商,要求0除以5等于几,可以先想哪个数和5相乘得0。
根据学生回答,得出:0×5=0,所以0÷5=0。
(2)师:0÷2和0÷8的商分别是多少?(点名学生回答)
(3)引导学生观察上面三个算式,总结算式结果都为0的共同特点。
教师小结:0除以任何不是0的数,都得0。(板书)
2.教学教材第23~24页例6。
(课件出示教材第23~24页例6的情境图和问题)
(1)组织学生看图,理解题意,说一说从图中得到了哪些信息?题目问题是什么?应该如何列式计算?(点名学生回答)
根据学生的回答分别板书:
①208÷2=________
②216÷2=________
(2)组织学生笔算第①题,教师巡视,观察学生笔算中的问题,根据观察的情况,点名学生板演。
组织学生就以下问题进行交流讨论。
①被除数十位上的0除以2得几?
②除得的商写在哪个数位的上面?
③商中间十位上的0可以不写吗?为什么?
引导学生明确:商十位上的0在这里起到占位的作用,如果不写,商就变成了14,结果就错误了,因此十位上的0不能不写。
师:十位上0÷2=0,可以直接在商的十位上写0,这一步不必再写竖式的计算过程。(教师板书下面竖式)
(3)组织学生笔算第②题,教师巡视,点名笔算错误的学生进行板演,全班学生发现问题并改正。
师:这道题中,十位上的1除以2,不够商1,我们应该怎么办?(点名学生回答)
引导学生明确:商的十位上不够除可以写0占位,再把被除数十位上的1和个位上的6合起来,计算16÷2。
教师板书简便写法。
(4)师:通过例6的这两个问题,你能说一说笔算除法的商什么时候需要用0占位吗?(小组交流讨论,点名小组代表回答,教师点评总结)
教师小结:在笔算除法的过程中,求出商的最高位上的数后,除到被除数的哪一位不够商1,就在哪一位商0占位。(板书小结)
三、巩固反馈
完成教材第24页“做一做”。(学生独立完成,集体订正)
第1题:0 0 0
第2题:201 203 205 104
第3题:606÷2=303(元)
828÷4=207(元)
303-207=96(元)
四、课堂小结
通过本节课的学习,你有什么收获?
板书设计
商中间有0的笔算除法
例5:0÷5=0 0÷2=0 0÷8=0
0除以任何不是0的数,都得0。
例6:
(1)
208÷2=104(元)
答:每套花了104元。
(2)
216÷2=108(元)
答:每套花了108元。
在笔算除法的过程中,求出商的最高位上的数后,除到被除数的哪一位不够商1,就在哪一位商0占位。
教学反思
1.在教学中,要让学生采用尝试、探究、讨论的方法,通过交流、讨论,使学生明白当除到被除数的某一位上不够商“1”时,就商“0”占位,同时在用竖式书写时,这一过程可以省略。利用旧知识学习新知识,培养学生知识迁移的能力。
2.在教学例6时,放手让学生自主笔算208÷2和216÷2。根据学生的笔算情况,把错误的与正确的,复杂的与简便的竖式进行对照,让学生在对比中理解。这样使学生经历自主探索商中间有0的笔算除法的过程,会更容易理解和掌握这样的除法计算,起到举一反三的作用。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】6□3÷3,要使商的中间有0,□里可以填( )。
分析:通过分析算式可知,要使商的中间有0,有两种情况:第一种情况是被除数中间的数是0,此时商的中间就有0;第二种情况是被除数中间的数比除数小,不够商1,商的中间同样有0,这时□里可以填1或2。
解答: 0、1、2
相关知识阅读
“0”的来历
大约1500年前,欧洲的数学家们是不知道用“0”的。他们使用罗马数字。罗马数字是用几个表示数的符号,按照一定规则,把它们组合起来表示不同的数字。在这种数字的运用里,不需要“0”这个数字。
而在当时,罗马帝国有一位学者从印度记数法里发现了“0”这个符号。他发现,有了“0”,进行数学运算方便极了,他非常高兴,还把印度人使用“0”的方法向大家做了介绍。过了一段时间,这件事被当时的罗马教皇知道了。当时是欧洲的中世纪,教会的势力非常大,罗马教皇的权利更是远远超过皇帝。教皇非常恼怒,于是下令把这位学者抓了起来,并对他施加了酷刑,用夹子把他的十个手指头紧紧夹住,使他两手残废,让他再也不能握笔写字。就这样,“0”被那个愚昧、残忍的罗马教皇明令禁止了。
但是,虽然“0”被禁止使用,然而罗马的数学家们还是不管禁令,在数学的研究中仍然秘密地使用“0”,仍然用“0”做出了很多数学上的贡献。后来“0”终于在欧洲被广泛使用,而罗马数字却逐渐被淡化了。
第5课时 商末尾有0的笔算除法
课时目标导航
教学导航
一、教学内容
商末尾有0的笔算除法。(教材第25页例7)
二、教学目标
1.使学生在熟练掌握一位数除三位数笔算除法的基础上,会正确计算商末尾有0的笔算除法。
2.通过自主探究和小组合作,让学生理解一位数除三位数,商末尾有0的笔算的算理并牢记规律。
3.培养学生对数学学习的兴趣。
三、重点难点
重点:掌握商末尾有0的除法的笔算方法,并能正确进行计算。
难点:理解商末尾有0的除法的计算算理。
教学过程
一、复习引入
笔算。
(1)424÷4= (2)505÷5=
组织学生独立笔算,并用乘法进行验算。
师:上一节课我们学习了商中间有0的笔算除法,今天我们继续学习商末尾有0的笔算除法。(板书课题:商末尾有0的笔算除法)
二、学习新课
1.教学教材第25页例7。
(课件出示教材第25页例7)
(1)师:从图中我们可以知道哪些信息?问题是什么?
明确:每根短跳绳5元,每根长跳绳8元。
问题1:求650元买短跳绳,可以买多少根。
问题2:求245元买长跳绳,可以买多少根,还剩多少钱。
(2)引导学生用除法解决问题1,列式为650÷5=________(根)。(板书算式)
组织学生笔算,教师巡视,根据学生笔算情况,点名学生板演。
组织学生就以下问题进行交流讨论。
①被除数个位上的0除以5得几?
②除得的商写在哪个数位上?
③商末尾的0可以省略不写吗?
教师一边讲解笔算方法,一边示范笔算。
师:用竖式计算650÷5时,先用5去除被除数百位上的6,在商的百位上写1,余下的1个百和5个十合成15个十,5除15个十商3,3写在商的十位上,个位上的0除以5得0,直接在商的个位上写0,其中0减去商和除数的乘积0的步骤可以省略不写。
师:与商中间有0的除法一样,在这里,商末尾的0也不可以不写。因为0在这里仍然起到占位的作用,如果不写,商就是13,结果就是不正确的。
(3)引导学生用除法解决问题2,列式为245÷8=________(根)……________(元)。(板书算式)
组织学生独立笔算,并将计算的过程和方法在小组中交流、讨论。
教师一边讲解笔算方法,一边示范笔算。
师:笔算时,先看被除数百位上的数,百位上的数不够除时,再看被除数的前两位,用8去除被除数百位和十位合成的数“24”,8除24得3,在商的十位上写3,接着用8去除被除数个位上的5,8除5不够商1,在商的个位上写0,被除数的个位上还余5,表明这是一道有余数的除法算式。
(4)引导学生用“除数×商+余数=被除数”来验算有余数的除法。
教师板书验算方法。
验算:
2.商末尾有0的除法的两种情况。
师:通过本节课的学习,同学们能说一说哪些情况下商末尾会是0吗?(小组交流讨论,点名小组代表回答,教师点评总结)
教师总结商末尾有0的除法的两种情况。(课件出示小结)
①除到被除数十位正好除尽,个位又是0,就不必再除下去,只要在个位上商0就可以。
②除到被除数十位正好除尽,而被除数个位上的数比除数小,就不必再除,只要在商的个位上写0,落下被除数个位上的数作余数即可。
三、巩固反馈
1.完成教材第25页“做一做”。(学生独立完成,同桌之间相互订正,点名学生说一说这四个除法算式有什么联系和区别,应该如何验算)
150 140 210……1 140……3(竖式略)
2.完成教材第27页“练习五”第9题。(学生独立完成,集体证正)
840÷7=120(千米)
四、课堂小结
通过本节课的学习,你有哪些收获?
板书设计
商末尾有0的笔算除法
例7:(1)650÷5=130(根) (2)245÷8=30(根)……5(元)
验算:
答:650元买短跳绳,可以买130根。 答:245元买长跳绳,可以买30根,还剩5元。
教学反思
1.教学中通过引导学生回顾上节课所学的内容来引入新知,放手让学生独立思考,大胆提问,自主探究,合作交流,让学生从自主学习中感受学习过程和解题思路,明白每一步算式的意义,培养学生的解题能力。
2.让学生从自己比较熟悉的情境入手,提出数学问题,这样能更好地激发学生解决问题的欲望,并使他们感受到了数学与日常生活有着密切的联系,取得了良好的教学效果。
3.为学生提供实践活动的机会,使学生通过实践活动,在一种愉悦的氛围中不知不觉地汲取数学养分,亲身经历运用数学知识解决简单的实际问题的过程,再一次真切地感受到了数学就在我们身边,从而激发了学生学数学、用数学的兴趣。
4.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】小明家距学校600米。一天,小明去上学,当他走了5分钟后,距离学校还有50米,小明平均每分钟走多少米?
分析:已知小明家距学校600米,5分钟后,距离学校还有50米,则走了的距离是600-50=550(米)。要求小明平均每分钟走多少米,就要用走了的距离除以所用的时间。
解答:600-50=550(米)
550÷5=110(米)
答:小明平均每分钟走110米。
相关知识阅读
跳绳的起源
中国古代很早就已经有了跳绳这种运动。过去的人称“跳绳”为“跳索”,《宛署杂记》载:“跳百索:(正月)十六日,儿以一绳长丈许,两儿对牵,飞摆不定,令难凝视,似乎百索,其实一也。群儿乘其动时,轮跳其上,以能过者为胜,否则为索所绊,听掌绳者绳击为罚。”这就是双人摇绳,多人轮跳的游戏方式。
而绳子在孩子们眼中更是童年不可或缺的玩具之一。跳绳属于我国的文化遗产,属于我们的民俗运动,更应加以发扬光大。
第6课时 练习课
课时目标导航
教学导航
一、教学内容
商中间或末尾有0的笔算除法的运用练习。(教材第26~27页练习五第3、4、5、8题)
二、教学目标
1.巩固商中间或末尾有0的笔算除法计算,并结合生活实际进行计算。
2.通过练习,使学生进一步掌握商中间或末尾有0的除法计算,提高计算的正确率。
3.在练习的过程中培养学生自主学习的习惯和态度。
三、重点难点
重点:巩固商中间或末尾有0的笔算除法计算。
难点:提高计算的正确率。
教学过程
一、基础练习
计算下列各题。
404÷4= 624÷6= 707÷7=
570÷3= 840÷7= 810÷8=
组织学生独立笔算,小组交流讨论商中间或末尾有0的除法的特征及计算方法。
二、指导练习
(课件依次出示各题)
1.教学教材第26页练习五第3题。
(1)组织学生看图,理解题意,明确已知条件和所求问题。
已知:全价票每张206元。
问题:求半价票每张多少钱。
(2)师:这里的半价票是什么意思?(点名学生回答)
引导学生明确:半价票的价格是全价票的价格的一半,求半价票的价格用除法计算,列式为206÷2。(板书算式)
(3)组织学生独立笔算,点名学生板演。教师根据学生板演总结商中间有0的除法特征。
师生共同小结:三位数除以一位数,当被除数百位刚好被除数整除,十位上是0时,这样的三位数通常商中间会出现0。(课件出示小结)
2.教学教材第26页练习五第4题。
(1)引导学生明确:“今年一共设了816个人工鸟巢,是去年的4倍”,求“去年设了多少个人工鸟巢”,用除法计算,列式为816÷4。(板书算式)
组织学生独立笔算,互相订正笔算过程及结果。
(2)师:被除数十位上的商是几?(点名学生回答)
师:这类商中间有0的除法有什么特征?应该怎样计算?(小组交流讨论,点名小组代表回答,教师点评总结)
师生共同小结:三位数除以一位数,当被除数的十位不够商“1”时,要商“0”占位,余下的数和个位上的数合起来继续除。(课件出示小结)
3.教学教材第27页练习五第5题。
(1)组织学生独立完成笔算,点名学生说一说哪些除法算式的商中间有0,哪些除法算式的商末尾有0。
(2)师:后面四个除法算式都有余数,对于有余数的除法,我们应该养成验算的习惯。你知道应该怎样验算吗?(点名学生回答)
引导学生明确:对于有余数的除法可以用“除数×商+余数=被除数”来进行验算。
组织学生完成验算。
4.教学教材第27页练习五第8题。
(1)引导学生明确:求“汽车每小时行驶的距离是人步行的多少倍”用除法计算,列式为110÷5。(板书算式)
组织学生笔算,点名学生汇报,并根据学生计算结果板书答案。
师:商的末尾为什么不是0?(点名学生回答)
师:被除数百位上的数小于除数,看被除数的前两位,11÷5=2……1,余数1和个位上的0合并成10,10÷5=2,所以商的末尾是2不是0。
(2)引导学生明确:求“飞机每小时飞行的距离是人步行的多少倍”用除法计算,列式为950÷5。(板书算式)
组织学生笔算,点名学生汇报,并根据学生计算结果板书答案。
师:这里商的末尾为什么是0?(点名学生回答)
三、巩固练习
完成教材第27~28页“练习五”第6、7、10、11、13题。(点名学生板演第6题,学生独立完成第7、10、11、13题,集体订正)
第6题:都错误,改正如下:
第7题:520÷5=104(把)
520÷8=65(把)
第10题:134……1 125……2 280 421(竖式,验算略)
第11题:略
第13题:30
四、课堂小结
通过本堂练习课,你有什么收获?
板书设计
练习课
3.206÷2=103(元)
答:半价票每张103元。
4.816÷4=204(个)
答:去年设了204个人工鸟巢。
8.(1)110÷5=22
答:汽车每小时行驶的距离是人步行的22倍。
(2)950÷5=190
答:飞机每小时飞行的距离是人步行的190倍。
教学反思
1.本课时是练习课,是对前几个课时的巩固,练习的目的是希望学生进一步了解商中出现0的情况。针对性练习提高了学生自主参与探索商中0的位置的积极性,也强化了学生对相关知识的理解和运用能力,充分发挥了练习课的巩固作用。
2.通过练习,也可以发现学生存在的一些问题,比如:有些学生读题能力不强,归纳分析的能力也有所欠缺,需要教师在课堂中多让学生进行这方面的练习,再进行指正,而不是直接将答案公之于众。通过“练习—归纳”“归纳—练习和演绎”的过程,让学生既能灵活运用知识,又能提高归纳能力。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】要使4□□÷3的商的末尾是0,被除数可能是多少?
分析:要使商的末尾是0,则除到被除数的十位正好除尽,且个位上的数字比3小。所以个位上的数字可能是0、1、2,十位上的数字可能是2、5、8,所以□□可能是20、21、22、50、51、52、80、81、82。
解答:被除数可能是420、421、422、450、451、452、480、481、482。
解法归纳:根据商末尾有0的除法的特征可确定被除数各数位上的数字,从而确定被除数。
第7课时 估算的应用
课时目标导航
教学导航
一、教学内容
估算的应用。(教材第29~30页例8、例9)
二、教学目标
1.使学生掌握运用估算解决实际问题的方法。
2.使学生学会从多角度思考来解决问题,培养学生灵活运用各种方法解决问题的能力。
3.通过在具体情境中进行除法估算,学会表达估算的思路,形成估算的习惯和意识。
三、重点难点
重点:掌握三位数除以一位数的估算方法,并利用其解决问题。
难点:结合实际情况,灵活应用估算策略解决问题。
教学过程
一、复习引入
1.口算。
60÷3= 250÷5= 180÷9=
1200÷6= 420÷7= 267÷3=
2.一个羽毛球6元,买28个羽毛球大约多少钱?
师:有一些算式我们很难快速口算出准确的结果。在日常生活中,很多时候我们也不需要计算出准确的结果,而只要计算出大约等于多少就行了,这就要求我们会估算。我们已经学过了三位数加、减法的估算和两位数乘一位数的估算,今天我们继续学习除法估算的问题。(板书课题:估算的应用)
二、学习新课
1.教学教材第29页例8。
(课件出示教材第29页例8)
组织学生看图,理解题意,说一说已知条件和所求问题分别是什么。
师:这里的“大约”是什么意思?(点名学生回答)
引导学生明确:“大约”表示估算,不需要准确计算出每天的住宿费,因此计算结果不能用“=”而只能用“≈”连接。根据“每天的住宿费=总钱数÷住的天数”列式计算。
教师板书:267÷3≈________(元)。
(1)探究估算的方法。
师:要使计算简单,我们可以估算成接近的整百数或几百几十数除以一位数。这道算式中,你准备把267看成哪个数来计算呢?(小组交流讨论,点名小组代表回答,教师板书)
方法一:把267看作与它接近的整百数:300。
267÷3≈100(元)
?
300
方法二:把267看作与它接近的几百几十数:270。
267÷3≈90(元)
?
270
(2)体会估算方法的合理性。
师:我们可以看到,两种方法估算出来的结果并不一样,那么这两种估算方法都合理吗?(小组交流讨论,点名小组代表回答)
引导学生明确:两种估算方法都是正确的,虽然估算出来的结果存在差异,但这种差异在这个问题中是可以忽略不计的。
师:你能通过上面的估算结果判断每天的住宿费比90元多还是比90元少吗?比80元呢?(点名学生回答)
引导学生明确:将267看成270,估算出来的结果是每天的住宿费是90元,被除数变大了,所以商也变大了,所以每天的住宿费比90元少。因为80×3=240<267,所以每天的住宿费比80元多。
教师小结:估算除数是一位数的除法,除数不变,把被除数看成能被整除的整十(百)数或几百几十(几千几百)数,再用口算除法的方法进行计算。(课件出示小结)
2.教学教材第30页例9。
(课件出示教材第30页例9)
组织学生看图,理解题意,说一说已知条件和所求问题分别是什么。
师:“够装”是什么意思?(点名学生回答)
引导学生明确:“够装”是指18个纸箱能装下的菠萝的个数不能少于所摘菠萝的总个数。
师:那么18个纸箱够装吗?需要先算出18个纸箱能装下的菠萝个数吗?(点名学生回答)
(1)探究估算的方法。
师:这个问题,可以用估一估的方法来解决。可以算算18个纸箱大约能装下多少个菠萝,还可以算算182个菠萝大约需要多少个纸箱。你能用这两种方法求解吗?(点名学生回答,教师板书)
方法一:18≈20,20×8=160(个),182>160,18个纸箱不够装。
方法二:182≈180,180÷8>20,18个纸箱不够装。
(2)检验估算结果的正确性。
师:到底需要多少个纸箱才能装下呢?这个问题应该如何解决?(组织小组讨论,独立计算,点名汇报)
引导学生用除法计算,根据计算可得,182除以8得22还余6,说明装了22个纸箱后,还剩6个,所以需要23个纸箱。因此18个纸箱不够,上面的估算方法是合理的。
三、巩固反馈
1.估算。(点名学生回答,并说一说自己的估算方法,集体订正)
640÷7≈90 231÷6≈40 469÷8≈60
176÷9≈20 146÷3≈50 330÷4≈80
2.书店买进了725本书,现在共有9个书架,每个书架可以放78本书,够放吗?(小组交流讨论,点名小组代表回答,集体订正)
78≈80 80×9=720(本)
720<725,不够放。
四、课堂小结
通过本节课的学习,你对估算的应用还有哪些疑问?
板书设计
估算的应用
教学反思
1.除法的估算和以前的四舍五入的估法有一些区别,以前的估算以乘法为主,借助乘法口诀或者整十整百数容易计算的特点,将其中的乘数估成比较接近的整十整百数再进行计算,如49×8,将49估成离它最近的整十数50,然后再计算50×8=400。但是除法的估算不能只考虑与被除数比较接近的整十或整百数,还有整除与否的关系,如401÷7,如果按照乘法估算的原则估成接近的整百数,那就得将401估成400,再计算400÷7,可是根据具体的情况看,400÷7不能整除,这样估算的结果并不简便,估算的意义也就不大了。再比如500÷7,500本身就是个整百数,按照以前估算的方法就不用再估了,可是500并不能被7整除,所以要将500估成490,再计算490÷7=70。因此,在除法估算的教学中,一定要把握好两个原则:一是要比较接近被除数;二是要能够整除。只有同时满足这两个条件,除法的估算才能顺利进行,才能体现出估算的意义。
2.本节课教学的目的不是单纯地教会学生如何去估算,而是要培养学生的估算意识,使不同的算法、算理和谐地统一在解决同一个问题的过程中,使学生在解决同一个问题时会选用不同的计算方法。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】5名教师带领233名学生去划船,每条船限坐8人,大约需要租多少条船?
分析:先用“5+233”求出总人数,然后根据每条船最多可坐8个人,求一共需要多少条船,即求总人数里面有几个8,根据求一个数里面有几个另一个数,用除法解答。
解答:233+5=238(人)
238÷8≈30(条)
答:大约需要租30条船。
相关知识阅读
草船借箭
三国时期,曹操率大军想要征服东吴,孙权、刘备联合抗曹。孙权手下有位大将叫周瑜,智勇双全,可是心胸狭窄,很妒忌诸葛亮的才干。因水中交战需要箭,周瑜要诸葛亮在十天内负责赶造十万支箭,哪知诸葛亮只要三天,还愿立下军令状,完不成任务甘受处罚。周瑜想,三天不可能造出十万支箭,正好利用这个机会来除掉诸葛亮。于是他一面叫军匠们不要把造箭的材料准备齐全,另一方面叫大臣鲁肃去探听诸葛亮的虚实。 鲁肃见了诸葛亮。诸葛亮说:“这件事要请你帮我的忙。希望你能借给我20只船,每只船上30个军士,船要用青布幔子遮起来,还要一千多个草把子,排在船两边。不过,这事千万不能让周瑜知道。” 鲁肃答应了,并按诸葛亮的要求把东西准备齐全。两天过去了,不见一点动静,到第三天四更时,诸葛亮秘密地请鲁肃一起到船上去,说是一起去取箭。鲁肃很纳闷。 诸葛亮吩咐把船用绳索连起来向对岸开去。 那天江上大雾迷漫,对面都看不见人。当船靠近曹军水寨时,诸葛亮命船一字摆开,叫士兵擂鼓呐喊。曹操以为对方来进攻,又因雾大怕中埋伏,就从旱寨派六千名弓箭手朝江中放箭,雨点般的箭纷纷射在草把子上。过了一会儿,诸葛亮又命船掉过头来,让另一面受箭。 太阳出来了,雾要散了,诸葛亮令船赶紧往回开。此时顺风顺水,曹操想追也来不及了。这时船的两边草把子上密密麻麻地插满了箭,诸葛亮让士兵将其中一只船上的箭拔下来数了数,共5346支。听了士兵的报告,诸葛亮笑了笑,说:“好了,这里的箭够十万支了。”你知道诸葛亮是怎么知道箭够十万支的吗?
第8课时 估算的应用(练习课)
课时目标导航
教学导航
一、教学内容
估算的运用练习。(教材第31~32页练习六第3、5、7题)
二、教学目标
1.使学生了解估算在日常生活中的重要性,进一步掌握除法估算的方法,提高学生的估算意识和能力。
2.通过练习,进一步提高学生的估算能力。
3.在练习的过程中培养学生勇于探索、敢于发现问题的精神。
三、重点难点
重点:掌握估算方法,能正确进行估算。
难点:能联系生活实际,灵活运用估算方法。
教学过程
一、基础练习
估算。
87÷9≈ 152÷8≈ 344÷7≈
175÷6≈ 134÷5≈ 273÷4≈
二、指导练习
(课件依次出示各题)
1.教学教材第31页练习六第3题。
组织学生看图,理解题意,找出已知条件和所求问题,说一说如何列式计算。
根据学生回答,板书算式:148÷3。
引导学生将148看成150估算,150是能被3整除的几百几十数,计算简便。
组织学生估算,板书学生估算结果。
师:每件T恤衫实际的售价比50元高还是低?为什么?(点名学生回答)
2.教学教材第32页练习六第5题。
师:两位老师打的字时间不一样,如何比较哪位老师打字打得更快?(点名学生回答)
引导学生根据“打字速度=打字个数÷打字时间”来比较。
师:需要算出两位老师每分钟打字的准确个数吗?(点名学生回答)
师:这里只需要比较大小,因此,我们可以通过估计值来比较。
组织学生估算,点名学生汇报估算方法和结果。根据学生回答,教师板书:
王老师:385÷4≈100(个)
李老师:512÷5≈100(个)
把385看作400是看大了,把512看作500是看小了,所以李老师打字打得更快。
3.教学教材第32页练习六第7题。
组织学生看图,理解题意,明确已知条件和所求问题。
师:如何判断能否把苹果、梨和香蕉都装上车?(小组交流讨论,点名小组代表回答)
学生给出方法:先求出苹果、梨和香蕉的总质量,再与1吨进行比较。
组织学生计算,根据学生计算结果板书:25×9+25×8+25×7=600(千克)。
师:大家还记得1吨等于多少千克吗?(学生齐答)
师:因为600千克小于1000千克,也就是1吨,所以能把苹果、梨和香蕉都装上车。
三、巩固练习
完成教材第31~32页“练习六”第1、2、4、6题。(点名学生回答第1题,给出估算结果和方法,集体订正。学生独立完成第2、4、6题,教师巡视指导,完成后小组间订正并相互交流)
第1题:20 70 30 10 60 70
第2题:255÷4≈60(个)
第4题:(1)128÷6≈20
(2)提问不唯一,例如:比目鱼的寿命大约是青蛙的多少倍?
64÷6≈10
第6题:256÷3≈85(册)
345÷4≈86(册) 478÷5≈96(册)
85<86<96,三年级平均每班捐赠图书的册数最多。
四、课堂小结
通过本节课的练习,你掌握了用估算解决实际问题的方法了吗?
板书设计
估算的应用(练习课)
3.148÷3≈50(元)
答:每件T恤衫大约50元。
5.王老师:385÷4≈100(个)
李老师:512÷5≈100(个)
把385看作400是看大了,把512看作500是看小了,所以李老师打字打得更快。
7.25×9+25×8+25×7=600(千克)
600千克<1吨 把苹果、梨和香蕉都装上车,行。
教学反思
1.估算是小学数学的一个重要内容。教学本节课时,着重抓住两个重要环节。第一,充分利用教材提供的现实情境,努力让学生回想起已有的知识和经验,鼓励学生用自己的方法估算,让学生通过与其他人的合作和交流,互相启发,打开思路,并引导学生进行自我练习,提高估算水平。第二,针对学生对估算把握不好的情况,多给学生独立思考和练习的时间,并适时地给予点拨,帮助学生更好地把握估算。
2.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】在□里填上适当的数,使算式满足条件。
(1)4□1÷2的商大约是200。
(2)□67÷3的商大约是300。
分析:(1)4□1÷2的商大约是200,因为200×2=400,所以4□1是一个接近400的数,根据四舍五入法,十位上的数应该小于5,即□里可以填0、1、2、3、4。
(2)□67÷3的商大约是300,因为300×3=900,被除数十位上的数是6,所以□里应该填8。
解答:(1)□里可以填0、1、2、3、4
(2)□里填8
解法归纳:先用除数和商相乘,求得被除数的估计值,再根据四舍五入法确定□里的数的可能取值。
相关知识阅读
估算的方法
1.去尾法。即把每个数的尾数去掉,取整十数或整百数进行计算。如计算524、208、602、310、219的和,把尾数去掉,取整百数相加,得到524+208+602+310+219≈500+200+600+300+200=1800。
2.进一法。即在每个数的最高位上加1,取整十或整百数进行计算。如28+15+7+24≈30+20+10+30=90。
3.四舍五入法。即尾数小于或等于4的舍去,大于或等于5的则进一,取整十或整百数进行计算。如42×18≈40×20=800。
4.根据部分求整体。即把一个大的整体平均分成若干份,根据部分数求出整体数。如估计体育场内的观众数,先将每个看台平均分成若干份,数一数其中的一份有多少人,然后估计出一个看台的人数,最后根据看台数推算出整个体育场的人数。
第1课时 两位数除以一位数的笔算
课时目标导航
教学导航
一、教学内容
两位数除以一位数的笔算。(教材第15~16页例1、例2)
二、教学目标
1.使学生在理解算理的基础上初步掌握一位数除两位数,商是两位数的计算方法。
2.培养学生观察、分析、推理、概括的能力。
3.掌握除法竖式的书写格式,培养学生认真审题的习惯。
三、重点难点
重点:掌握一位数除两位数的笔算方法,能正确计算一位数除两位数。
难点:掌握一位数除两位数,商是两位数的笔算过程中的试商方法。
四、教学准备
教师准备:课件PPT、小棒。
学生准备:小棒。
教学过程
一、情境引入
师:同学们,你们知道植树节是哪一天吗?(学生齐答)
师:对,就是3月12日。每年的3月12日是植树节,这天人们都会去植树。今年的植树节,三年级和四年级的同学们也去植树了,我们一起去看看吧!(课件出示教材第15页例1情境图)
师:从图中你知道了哪些信息?你能提出哪些问题?(点名学生回答)
组织学生观察情境图,使学生明确:三年级两个班共要种树42棵,四年级两个班共要种树52棵。
师:知道了两个班要种树的总数,我们就可以求平均每班要种多少棵树。
师:我们已经学习了商是一位数的笔算除法,商是两位数的口算除法,那么用两位数除以一位数的笔算,又该怎样计算呢?今天这节课,我们就来学习这部分内容。(板书课题:两位数除以一位数的笔算)
二、学习新课
1.教学教材第15页例1。
(1)师:要求三年级平均每班种多少棵树,应怎样列式?(点名学生回答,教师板书)
师:42÷2还能够利用我们前面所学的口算方法计算吗?你是怎样想的?(点名学生回答)
(2)组织学生汇报。
(3)组织学生以小组为单位,动手分一分。
取4捆小棒(40根)和2根散棒,一共42根,把这些小棒平均分成2份。让学生在小组中交流讨论,应该怎样分。
师:我们可以先把4捆小棒分成2份,每份2捆,也就是先用4个十除以2,得到2个十;再把2根散棒分成2份,每份1根,也就是用2个一除以2,得到1个一,合起来就是21根。(教师演示分小棒过程,课件出示分小棒图)
师:21就是42÷2的商,求得的商是两位数,以前我们学习了商是一位数的笔算除法,现在出现了商是两位数的除法,根据刚才分小棒的过程,同学们会不会列竖式笔算呢?(学生独立完成,教师巡视指导)
板书下面的竖式,教师讲解算理,明确书写要求。
师:因为我们在分小棒时,是先分整捆的,所以在竖式计算中就要先分十位上的数。在42中,4在十位上,我们从整十数除起,4个十除以2,应该得2个十,2个十要写在十位“4”的上面。再用2个十乘2,应该得4个十,这个4应该写在被除数十位“4”的下面,表示从被除数中分掉的数是40,为了简便,0可以省略不写,再用4减4得0。表示被除数中的整十数正好分完。接着我们再求商的个位,从图上看,分完了整捆的,还有2根没有分,从竖式看十位数正好分完,还有个位上的2没有分。我们继续求商的个位,在竖式中把个位上的2落下来,用求商的十位的方法来求出商的个位。2个一除以2,得1个一,商1写在被除数个位“2”的上面。得出42÷2的商是21。
(4)师生共同小结。
笔算两位数除以一位数,当十位可被整除时,先用一位数去除被除数十位上的数,商写在十位的上面,再用一位数去除个位上的数,商写在个位的上面。(课件出示小结)
2.教学教材第16页例2。
(1)师:要求四年级平均每班种多少棵,应怎样列式?(点名学生回答,教师板书)
(2)组织学生动手分小棒,用分小棒的方法求解这个问题。
师:你在分小棒的过程中遇到了什么问题吗?(点名学生回答)
师:52÷2也就是把52根小棒(5捆和2根)平均分成2份。先把5捆平均分成2份,每份是2捆(20根),还余1捆。这1捆应该怎么分呢?(小组交流讨论)
师:对了,我们可以把剩下的1捆(10根)拆开,与2根合起来是12根,再把12根平均分成2份,每份是6根,加起来共分得26根,所以52÷2=26。(教师演示分小棒过程,课件出示分小棒图)
(3)引导学生将分小棒求解的过程写成除法竖式的形式。(学生独立完成,教师巡视指导)
板书下面的竖式,教师讲解算理,明确书写要求。
(4)师生共同小结。
笔算两位数除以一位数,当十位不可被整除时,先用一位数除被除数十位上的数,把余数和个位上的数合并,再用除数去除,除到被除数的哪一位,就把商写在哪一位的上面。(课件出示小结)
(5)师:这个除法竖式计算过程比较复杂,怎么知道我们的计算结果是否正确呢?你有什么好的建议吗?(引导学生提出验算)
师:不错,为了检验较复杂的除法的计算结果是否正确,我们可以进行验算。在没有余数的除法中,如果“除数×商=被除数”,那么说明原来的除法计算正确,否则计算不正确,需要重新计算。(点名学生板演,检验计算结果的正确性)
3.比较例1和例2的异同点。
引导学生观察比较例1和例2笔算竖式的异同,组织学生互相交流,再点名汇报,集体补充。
相同点:都是从被除数十位上的数除起,除到被除数的哪一位,商就写在哪一位的上面。
不同点:例2的被除数十位上除后还有余数,要与个位上的数合起来再除。
三、巩固反馈
1.完成教材第16页“做一做”。(点名学生板演,其余学生独立完成,集体订正)
32 34 12 23 39 17
2.完成教材第19页“练习四”第1、2题。(点名学生板演第1题;点名学生指出第2题计算错误的笔算竖式,说明错误原因并板演改正)
第1题:13 31 22 11
17 25 14 14
第2题:第二个和第三个计算错误。改正如下:
四、课堂小结
谈谈对于一位数除两位数的笔算方法中有哪些需要注意或不太懂的地方。
板书设计
两位数除以一位数的笔算
例1:
42÷2=21(棵)
答:三年级平均每班种21棵。
例2:
52÷2=26(棵)
答:四年级平均每班种26棵。
教学反思
1.教学笔算两位数除以一位数的除法时,竖式的写法是一个难点,学生已有的经验在此时已经不够用了。所以在教学过程中,大部分时间都放在解决除的顺序和竖式的写法上。引导学生用数学语言来表述笔算除法的过程,让学生说出自己的思考过程。知道在做笔算除法时,一般应先算什么,再算什么,最后算什么,有一个合理的演算顺序。
2.计算是一个非常枯燥的内容,教师可利用学生的好胜心,采用小组竞赛的形式激发学生的学习兴趣。特意让平时掌握知识比较慢的,或者计算比较容易出错的学生板演,这样就可以及时地纠正他们的错误。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】某办公楼前安装了一排彩灯,按照4红,1黄,3绿的顺序排列,第88盏彩灯是什么颜色的?
分析:彩灯以(4+1+3)盏为一个周期不断重复排列,要想知道第88盏彩灯是什么颜色的,就要计算88盏彩灯里包含多少个这样的周期。如果正好是整数周期,说明第88盏彩灯的颜色正好是一个周期中最后一盏彩灯的颜色;如果有余数,余数是几,第88盏彩灯的颜色就是一个周期中第几盏彩灯的颜色。
解答:4+1+3=8(盏)
88÷8=11(个)
答:第88盏彩灯是绿色的。
解法归纳:此题属于周期问题,找到彩灯的排列规律是解此题的关键。
相关知识阅读
植树节
植树节是一些国家法律规定的以宣传保护森林,并动员群众参加以植树造林为活动内容的节日。按时间长短可分为植树日、植树周或植树月,总称植树节。通过这种活动,激发人们爱林、造林的热情,提高人们爱护森林的意识,促进国土绿化,达到爱林护林、扩大森林资源和改善生态环境的目的。植树节是为了动员全民植树而规定的节日。1979年2月23日,中华人民共和国第五届全国人大常务委员会第六次会议决定,以3月12日为中国的植树节,以鼓励全国各族人民植树造林,绿化祖国,改善环境,造福子孙后代。
第2课时 三位数除以一位数的笔算
课时目标导航
教学导航
一、教学内容
三位数除以一位数的笔算。(教材第17~18页例3、例4)
二、教学目标
1.使学生掌握三位数除以一位数的笔算方法。
2.培养学生的验算意识。
3.培养学生认真计算的好习惯。
三、重点难点
重点:掌握三位数除以一位数的笔算方法,运用乘法验算除法。
难点:理解三位数除以一位数的算理。
教学过程
一、复习引入
1.口算。
24÷6= 52÷2= 70÷5=
42÷3= 64÷4= 68÷4=
2.笔算。
36÷3= 36÷2= 78÷3=
师:前面我们学习了两位数除以一位数的口算和笔算,那么,三位数除以一位数又该怎样计算呢?通过本节课的学习,相信同学们就能掌握方法。(板书课题:三位数除以一位数的笔算)
二、学习新课
1.教学教材第17页例3。
(课件出示教材第17页例3)
(1)创设情境,引出问题。
师:小梦和小欣是一对好姐妹,她们经常一起玩耍。今天,两人商量着拿出各自的照片,放在相册里。你们看,她们多认真啊!
组织学生观察情境图,说说从中可以知道哪些信息。(点名学生回答)
引导学生说出:小梦和小欣一共有256张照片,用2本这样的相册正好插完。
师:把256张照片插入2本相册中,求每本相册插多少张照片,应该如何列式呢?(点名学生回答,教师板书)
根据学生的回答教师板书:256÷2=________。
(2)尝试计算,探究新知。
师:你觉得今天学习的三位数除以一位数的计算和上节课学习的两位数除以一位数的计算有什么联系?(小组交流讨论,点名小组代表回答)
师:你能用以前学过的方法计算这道题吗?(引导学生尝试用笔算的方法计算)
教师讲解三位数除以一位数的算理并板书竖式计算过程。
师:三位数除以一位数的算理与两位数除以一位数的算理相同。笔算时,先用2去除被除数的首位,商1,将1写在商的百位上;将求得的商“1”与除数“2”相乘,得到2个百,将“2”写在被除数的百位下面,2减2等于0(0可以省略不写),表示被除数百位上的数已经被分完。接着,将被除数十位上的数“5”写下来,用2去除5,商2,将2写在商的十位上,2与除数“2”相乘得4,将4写在5下面,5减4得1,将1写在4的下面,再将被除数个位上的数“6”写下来,6与十位上的数合成“16”,2除16商8,将8写在商的个位上,8与除数“2”相乘得16,16减16等于0,将0写在余数的位置上。
(3)组织学生验算,检查计算结果是否正确。(点名学生板演验算过程,其他学生独立验算)
2.教学教材第18页例4。
(课件出示教材第18页例4)
(1)组织学生读题,理解题意,说一说从题中获得了哪些信息,问题是什么。(点名学生回答)
引导学生明确:要求可插满多少页,还剩多少张照片用除法计算,除得的商就是页数,余数就是张数。
学生列出算式,教师板书:256÷6=_________(页)……________(张)。
(2)师:大家用竖式算一算,看看计算过程与例3中的三位数除以一位数有什么不同。(小组交流讨论,点名小组代表回答)
师:相信同学们都发现了,例3中的竖式,商是一个三位数,能够整除,而例4中的竖式,商是两位数,有余数。
教师一边板书一边讲解笔算方法。
师:写出竖式,先用被除数256百位上的2除以6,不够商1,再看被除数的前两位,2个百和5个十合起来是25个十,用25个十除以6,商4写在十位的上面,分掉了24个十,余下1个十。余下的1个十和个位上的6个一合起来是16个一,继续除以6,商2写在个位的上面,余数4比除数小。
提醒学生注意:计算除法时,如果除到被除数的个位,仍不能恰好除完,可以留有余数,但余数必须比除数小。
(3)师:对于有余数的除法,我们应该如何验算呢?(点名学生回答)
师:计算结束后,要验算我们的计算是否正确,根据“被除数=除数×商+余数”,我们可以计算42×6+4,看结果是否与被除数相等。(学生独立计算,教师板书验算过程)
验算:
教师强调验算的重要性,让学生养成计算后验算的习惯。
(4)师:通过上面两道例题,你能总结出三位数除以一位数的笔算方法吗?(小组交流讨论,点名小组代表回答)
教师小结:三位数除以一位数,先用除数去除被除数百位上的数,除得的商写在百位的上面;如果被除数百位上的数小于除数,就看被除数的前两位,商的最高位写在十位的上面。除到被除数的哪一位,就把商写在哪一位的上面。每次除得的余数都要比除数小。(课件出示小结)
三、巩固反馈
1.完成教材第17页“做一做”。(点名学生板演,其余学生独立完成,集体订正)
216 174 171 159(竖式,验算略)
2.完成教材第18页“做一做”。(点名学生回答每个竖式的商是几位数,说一说自己的判断理由,再点名学生板演,集体订正)
商是两位数的有:
商是三位数的有:
81……3 61 141……2 51……2(竖式,验算略)
四、课堂小结
对于三位数除以一位数的笔算方法还有哪些疑问?
板书设计
三位数除以一位数的笔算
例3:
256÷2=128(张)
答:每本相册插128张照片。
例4:
256÷6=42(页)……4(张)
答:可插满42页,还剩4张。
教学反思
1.本节课在教学中始终联系学生的生活实际,体现了数学与生活的密切联系。让学生合作学习、互相交流,不仅拓宽了学生的思维,还让每个学生都有了表达自己见解的机会,也培养了学生倾听的习惯。
2.好的评价在一定程度上能激励学生的学习,在本节课中,教师注重对学生的评价。及时对学生的发现进行肯定和表扬,不仅对发言者是一个激励,对其他学生而言,也是非常好的鼓励和鞭策。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】植树节到了,四、五年级的学生参加了义务植树活动,劳动结束时他们共植树129棵,五年级植树的棵数是四年级的2倍。四、五年级各植树多少棵?
分析:因为五年级植树的棵数是四年级的2倍,所以四、五年级学生共植树的129棵是四年级植树棵数的3倍,用四、五年级学生共植树的总棵数除以3即可得四年级植树的棵数,再求五年级植树的棵数即可。
解答:2+1=3
四年级:129÷3=43(棵)
五年级:43×2=86(棵)
答:四年级植树43棵,五年级植树86棵。
相关知识阅读
整除与除尽
整除与除尽既有区别又有联系。除尽是指数a除以数b(b≠0)所得的商是整数或有限小数而余数是0的情况,这时我们就说a能被b除尽(或说b能除尽a)。而只有当被除数、除数以及商都是整数,余数是0时,才能叫整除。也就是说,除尽并不局限于在整数范围内,只要余数是0就可以了。整除是除尽的特殊情况。
第3课时 练习课
课时目标导航
教学导航
一、教学内容
两位数、三位数除以一位数的运用练习。(教材第19~21页练习四第3、6、8、14题)
二、教学目标
1.巩固笔算除法中多位数除以一位数的计算方法及余数的处理方法。
2.通过练习,使学生进一步掌握笔算除法的相关规律,提高计算的效率。
3.在练习的过程中培养学生积极的参与态度和良好的学习习惯。
三、重点难点
重点:掌握笔算除法中的相关运算法则。
难点:提高运算的效率并能熟练运用笔算除法。
教学过程
一、基础练习
笔算。
46÷2= 96÷3= 48÷4=
126÷3= 224÷4= 336÷8=
129÷2= 250÷4= 199÷7=
引导学生根据被除数和除数的特点,判断商是几位数,同桌间相互说一说。
组织学生自主计算,然后互相交流算法,订正计算过程和结果。
二、指导练习
(课件依次出示各题)
1.教学教材第19页练习四第3题。
(1)引导学生看图,理解题意,用自己的语言描述已知条件及所求问题。(点名学生回答,教师板书问题)
问题1:小芳能摆多少组?
问题2:小东能摆多少组?
(2)师:按照小芳的摆法,求能摆多少组,应该如何列式计算?(点名学生回答)
组织学生独立计算,教师巡视,对学生竖式书写的规范性和计算过程进行指导。
引导学生通过验算来保证计算结果的正确性。
根据学生计算结果板书:96÷6=16(组)。
(3)按照上面同样的步骤组织学生列出算式、笔算、验算,求解问题2。
根据学生计算结果板书:96÷8=12(组)。
(4)师:这道题属于两位数除以一位数的笔算问题,同学们能说一说两位数除以一位数的笔算方法吗?(点名学生回答,教师点评总结)
师生共同小结:笔算两位数除以一位数,先用一位数除被除数十位上的数,如果有余数,就把余数和个位上的数合起来,再用除数去除,除到被除数的哪一位,就把商写在哪一位的上面。(课件出示小结)
2.教学教材第20页练习四第6题。
(1)师:我们可以先笔算,再判断商是两位数还是三位数,不过运算量比较大,同学们还能想出更好的办法吗?(小组交流讨论)
师:如果商是三位数,那么用一位数去除三位数时,一位数和被除数的最高位有什么大小关系?(点名学生回答)
引导学生明确:如果被除数最高位上的数字大于或等于除数,那么商就是三位数;否则,商就是两位数。因此可以通过比较被除数最高位上的数字和除数的大小来判断商的位数。
(2)组织学生用上面的方法判断四个除法算式的商的位数,并按要求涂色,完成后集体订正。
3.教学教材第20页练习四第8题。
(1)引导学生看图,理解题意,用自己的语言描述已知条件及所求问题。(点名学生回答)
师:求一个足球多少钱,应该如何列式?(点名学生回答)
组织学生独立笔算出结果,进行验算,教师巡视指导。
根据学生计算结果板书:272÷4=68(元)。
(2)师:你能说一说三位数除以一位数的笔算方法吗?(点名学生回答,教师点评总结)
教师小结:三位数除以一位数,先用除数去除被除数百位上的数,除得的商写在百位的上面,如果被除数百位上的数小于除数,就看被除数的前两位,商的最高位写在十位的上面。除到被除数的哪一位,商就写在哪一位的上面。每次除得的余数都要比除数小。(课件出示小结)
4.教学教材第21页练习四第14题。
(1)组织学生看图,明确已知条件和所求问题。
已知:阿姨带了100元,铅笔单价8元/盒。
问题:求最多可以买多少盒铅笔,还剩多少钱?
师:求最多可以买多少盒铅笔,还剩多少钱,应该怎样计算?
引导学生列出算式:100÷8=________(盒)……________(元)。
师:100除以8的商是几,就可以买几盒铅笔,余数是多少,就还剩多少钱。
组织学生独立计算,集体订正。
根据学生计算结果板书:100÷8=12(盒)……4(元)。
(2)师:像这样的有余数的除法应用题也是我们需要掌握的重点。首先我们需要判断是否该用除法算式解决问题,其次,要明白除法算式的商和余数与问题中的待求量的关系。
三、巩固练习
完成教材第19~22页“练习四”第4、5、10、13、18题。(学生独立完成,集体订正)
第4题:90÷2=45(张)
45÷3=15(张)
第5题:139 185 83 44(竖式、验算略)
第10题:
第13题:336÷8=42(分钟)
第18题:643÷5=128(盆)……3(盆)
四、课堂小结
通过本堂课的学习,你有什么收获?
板书设计
练习课
3.问题1:小芳能摆多少组? 问题2:小东能摆多少组?
96÷6=16(组) 96÷8=12(组)
答:小芳能摆16组。 答:小东能摆12组。
8.272÷4=68(元)
14.100÷8=12(盒)……4(元)
答:最多可以买12盒铅笔,还剩4元。
教学反思
1.本节练习课设计了多层次、多类型的练习,通过对不同类型题目的讲解和练习,使学生熟练掌握各种类型的笔算除法技巧和相关延伸运算方法。既包括对两位数、三位数除以一位数笔算方法的回顾,也包括三位数除以一位数的商的位数的判断的简单技巧介绍,还包括有余数除法的简单实际问题的讲解,通过丰富的练习,提高学生对笔算除法的运用能力。
2.针对不同类型的题目可以设计不同的练习形式。两、三位数除以一位数的笔算倡导学生自主计算,小组相互检查,订正计算过程和结果,再对计算方法进行总结。有关笔算除法的应用题,可以让学生结合条件和问题说一说,提高学生的理解能力,渗透具体问题具体分析的思想。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】一道除法算式,小明一时马虎,计算时把除数6看成了9,结果得32余8。正确的得数是多少?
分析:由题意,可知
对比两个算式发现,被除数是不变的。从错误的算式入手,根据“被除数=商×除数+余数”算出被除数=32×9+8=296,再用被除数除以正确的除数,就能算出正确的结果。
解答:32×9+8=296
296÷6=49……2
答:正确的得数是49余2。
解法归纳:解决此类问题时,应该抓住被除数这一不变量,利用“商×除数+余数=被除数”先求出被除数,再进行计算。
第4课时 商中间有0的笔算除法
课时目标导航
教学导航
一、教学内容
商中间有0的笔算除法。(教材第23~24页例5、例6)
二、教学目标
1.使学生知道0除以任何不是0的数都得0。
2.掌握一位数除三位数,商中间有0的除法的算理,会正确计算商中间有0的除法。
3.培养学生良好的计算习惯。
三、重点难点
重点:掌握商中间有0的除法的笔算方法,并能正确进行计算。
难点:理解0在商中的占位作用,能熟练地进行笔算并解决问题。
教学过程
一、复习引入
1.口算练习。
28÷2= 66÷6= 330÷3=
33-4= 0×2= 140÷2=
8×0= 540÷6= 28+0=
6×0=
师:0×2、8×0、6×0这三道题的得数是多少?
2.说一说。
(1)请学生说出数字39中3和9各表示的意义。
(2)请学生说出0表示的意义。
(3)在3和9的中间添上一个0,使39变成“309”,请学生说出0在这个位置表示的意义。
师:0÷8的结果是多少?309除以3又该怎样计算?我们就从这里开始我们今天的课程。(板书课题:商中间有0的笔算除法)
二、学习新课
1.教学教材第23页例5。
(课件出示教材第23页例5)
(1)师:你知道0除以5等于几吗?
引导学生想乘法求除法算式的商,要求0除以5等于几,可以先想哪个数和5相乘得0。
根据学生回答,得出:0×5=0,所以0÷5=0。
(2)师:0÷2和0÷8的商分别是多少?(点名学生回答)
(3)引导学生观察上面三个算式,总结算式结果都为0的共同特点。
教师小结:0除以任何不是0的数,都得0。(板书)
2.教学教材第23~24页例6。
(课件出示教材第23~24页例6的情境图和问题)
(1)组织学生看图,理解题意,说一说从图中得到了哪些信息?题目问题是什么?应该如何列式计算?(点名学生回答)
根据学生的回答分别板书:
①208÷2=________
②216÷2=________
(2)组织学生笔算第①题,教师巡视,观察学生笔算中的问题,根据观察的情况,点名学生板演。
组织学生就以下问题进行交流讨论。
①被除数十位上的0除以2得几?
②除得的商写在哪个数位的上面?
③商中间十位上的0可以不写吗?为什么?
引导学生明确:商十位上的0在这里起到占位的作用,如果不写,商就变成了14,结果就错误了,因此十位上的0不能不写。
师:十位上0÷2=0,可以直接在商的十位上写0,这一步不必再写竖式的计算过程。(教师板书下面竖式)
(3)组织学生笔算第②题,教师巡视,点名笔算错误的学生进行板演,全班学生发现问题并改正。
师:这道题中,十位上的1除以2,不够商1,我们应该怎么办?(点名学生回答)
引导学生明确:商的十位上不够除可以写0占位,再把被除数十位上的1和个位上的6合起来,计算16÷2。
教师板书简便写法。
(4)师:通过例6的这两个问题,你能说一说笔算除法的商什么时候需要用0占位吗?(小组交流讨论,点名小组代表回答,教师点评总结)
教师小结:在笔算除法的过程中,求出商的最高位上的数后,除到被除数的哪一位不够商1,就在哪一位商0占位。(板书小结)
三、巩固反馈
完成教材第24页“做一做”。(学生独立完成,集体订正)
第1题:0 0 0
第2题:201 203 205 104
第3题:606÷2=303(元)
828÷4=207(元)
303-207=96(元)
四、课堂小结
通过本节课的学习,你有什么收获?
板书设计
商中间有0的笔算除法
例5:0÷5=0 0÷2=0 0÷8=0
0除以任何不是0的数,都得0。
例6:
(1)
208÷2=104(元)
答:每套花了104元。
(2)
216÷2=108(元)
答:每套花了108元。
在笔算除法的过程中,求出商的最高位上的数后,除到被除数的哪一位不够商1,就在哪一位商0占位。
教学反思
1.在教学中,要让学生采用尝试、探究、讨论的方法,通过交流、讨论,使学生明白当除到被除数的某一位上不够商“1”时,就商“0”占位,同时在用竖式书写时,这一过程可以省略。利用旧知识学习新知识,培养学生知识迁移的能力。
2.在教学例6时,放手让学生自主笔算208÷2和216÷2。根据学生的笔算情况,把错误的与正确的,复杂的与简便的竖式进行对照,让学生在对比中理解。这样使学生经历自主探索商中间有0的笔算除法的过程,会更容易理解和掌握这样的除法计算,起到举一反三的作用。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】6□3÷3,要使商的中间有0,□里可以填( )。
分析:通过分析算式可知,要使商的中间有0,有两种情况:第一种情况是被除数中间的数是0,此时商的中间就有0;第二种情况是被除数中间的数比除数小,不够商1,商的中间同样有0,这时□里可以填1或2。
解答: 0、1、2
相关知识阅读
“0”的来历
大约1500年前,欧洲的数学家们是不知道用“0”的。他们使用罗马数字。罗马数字是用几个表示数的符号,按照一定规则,把它们组合起来表示不同的数字。在这种数字的运用里,不需要“0”这个数字。
而在当时,罗马帝国有一位学者从印度记数法里发现了“0”这个符号。他发现,有了“0”,进行数学运算方便极了,他非常高兴,还把印度人使用“0”的方法向大家做了介绍。过了一段时间,这件事被当时的罗马教皇知道了。当时是欧洲的中世纪,教会的势力非常大,罗马教皇的权利更是远远超过皇帝。教皇非常恼怒,于是下令把这位学者抓了起来,并对他施加了酷刑,用夹子把他的十个手指头紧紧夹住,使他两手残废,让他再也不能握笔写字。就这样,“0”被那个愚昧、残忍的罗马教皇明令禁止了。
但是,虽然“0”被禁止使用,然而罗马的数学家们还是不管禁令,在数学的研究中仍然秘密地使用“0”,仍然用“0”做出了很多数学上的贡献。后来“0”终于在欧洲被广泛使用,而罗马数字却逐渐被淡化了。
第5课时 商末尾有0的笔算除法
课时目标导航
教学导航
一、教学内容
商末尾有0的笔算除法。(教材第25页例7)
二、教学目标
1.使学生在熟练掌握一位数除三位数笔算除法的基础上,会正确计算商末尾有0的笔算除法。
2.通过自主探究和小组合作,让学生理解一位数除三位数,商末尾有0的笔算的算理并牢记规律。
3.培养学生对数学学习的兴趣。
三、重点难点
重点:掌握商末尾有0的除法的笔算方法,并能正确进行计算。
难点:理解商末尾有0的除法的计算算理。
教学过程
一、复习引入
笔算。
(1)424÷4= (2)505÷5=
组织学生独立笔算,并用乘法进行验算。
师:上一节课我们学习了商中间有0的笔算除法,今天我们继续学习商末尾有0的笔算除法。(板书课题:商末尾有0的笔算除法)
二、学习新课
1.教学教材第25页例7。
(课件出示教材第25页例7)
(1)师:从图中我们可以知道哪些信息?问题是什么?
明确:每根短跳绳5元,每根长跳绳8元。
问题1:求650元买短跳绳,可以买多少根。
问题2:求245元买长跳绳,可以买多少根,还剩多少钱。
(2)引导学生用除法解决问题1,列式为650÷5=________(根)。(板书算式)
组织学生笔算,教师巡视,根据学生笔算情况,点名学生板演。
组织学生就以下问题进行交流讨论。
①被除数个位上的0除以5得几?
②除得的商写在哪个数位上?
③商末尾的0可以省略不写吗?
教师一边讲解笔算方法,一边示范笔算。
师:用竖式计算650÷5时,先用5去除被除数百位上的6,在商的百位上写1,余下的1个百和5个十合成15个十,5除15个十商3,3写在商的十位上,个位上的0除以5得0,直接在商的个位上写0,其中0减去商和除数的乘积0的步骤可以省略不写。
师:与商中间有0的除法一样,在这里,商末尾的0也不可以不写。因为0在这里仍然起到占位的作用,如果不写,商就是13,结果就是不正确的。
(3)引导学生用除法解决问题2,列式为245÷8=________(根)……________(元)。(板书算式)
组织学生独立笔算,并将计算的过程和方法在小组中交流、讨论。
教师一边讲解笔算方法,一边示范笔算。
师:笔算时,先看被除数百位上的数,百位上的数不够除时,再看被除数的前两位,用8去除被除数百位和十位合成的数“24”,8除24得3,在商的十位上写3,接着用8去除被除数个位上的5,8除5不够商1,在商的个位上写0,被除数的个位上还余5,表明这是一道有余数的除法算式。
(4)引导学生用“除数×商+余数=被除数”来验算有余数的除法。
教师板书验算方法。
验算:
2.商末尾有0的除法的两种情况。
师:通过本节课的学习,同学们能说一说哪些情况下商末尾会是0吗?(小组交流讨论,点名小组代表回答,教师点评总结)
教师总结商末尾有0的除法的两种情况。(课件出示小结)
①除到被除数十位正好除尽,个位又是0,就不必再除下去,只要在个位上商0就可以。
②除到被除数十位正好除尽,而被除数个位上的数比除数小,就不必再除,只要在商的个位上写0,落下被除数个位上的数作余数即可。
三、巩固反馈
1.完成教材第25页“做一做”。(学生独立完成,同桌之间相互订正,点名学生说一说这四个除法算式有什么联系和区别,应该如何验算)
150 140 210……1 140……3(竖式略)
2.完成教材第27页“练习五”第9题。(学生独立完成,集体证正)
840÷7=120(千米)
四、课堂小结
通过本节课的学习,你有哪些收获?
板书设计
商末尾有0的笔算除法
例7:(1)650÷5=130(根) (2)245÷8=30(根)……5(元)
验算:
答:650元买短跳绳,可以买130根。 答:245元买长跳绳,可以买30根,还剩5元。
教学反思
1.教学中通过引导学生回顾上节课所学的内容来引入新知,放手让学生独立思考,大胆提问,自主探究,合作交流,让学生从自主学习中感受学习过程和解题思路,明白每一步算式的意义,培养学生的解题能力。
2.让学生从自己比较熟悉的情境入手,提出数学问题,这样能更好地激发学生解决问题的欲望,并使他们感受到了数学与日常生活有着密切的联系,取得了良好的教学效果。
3.为学生提供实践活动的机会,使学生通过实践活动,在一种愉悦的氛围中不知不觉地汲取数学养分,亲身经历运用数学知识解决简单的实际问题的过程,再一次真切地感受到了数学就在我们身边,从而激发了学生学数学、用数学的兴趣。
4.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】小明家距学校600米。一天,小明去上学,当他走了5分钟后,距离学校还有50米,小明平均每分钟走多少米?
分析:已知小明家距学校600米,5分钟后,距离学校还有50米,则走了的距离是600-50=550(米)。要求小明平均每分钟走多少米,就要用走了的距离除以所用的时间。
解答:600-50=550(米)
550÷5=110(米)
答:小明平均每分钟走110米。
相关知识阅读
跳绳的起源
中国古代很早就已经有了跳绳这种运动。过去的人称“跳绳”为“跳索”,《宛署杂记》载:“跳百索:(正月)十六日,儿以一绳长丈许,两儿对牵,飞摆不定,令难凝视,似乎百索,其实一也。群儿乘其动时,轮跳其上,以能过者为胜,否则为索所绊,听掌绳者绳击为罚。”这就是双人摇绳,多人轮跳的游戏方式。
而绳子在孩子们眼中更是童年不可或缺的玩具之一。跳绳属于我国的文化遗产,属于我们的民俗运动,更应加以发扬光大。
第6课时 练习课
课时目标导航
教学导航
一、教学内容
商中间或末尾有0的笔算除法的运用练习。(教材第26~27页练习五第3、4、5、8题)
二、教学目标
1.巩固商中间或末尾有0的笔算除法计算,并结合生活实际进行计算。
2.通过练习,使学生进一步掌握商中间或末尾有0的除法计算,提高计算的正确率。
3.在练习的过程中培养学生自主学习的习惯和态度。
三、重点难点
重点:巩固商中间或末尾有0的笔算除法计算。
难点:提高计算的正确率。
教学过程
一、基础练习
计算下列各题。
404÷4= 624÷6= 707÷7=
570÷3= 840÷7= 810÷8=
组织学生独立笔算,小组交流讨论商中间或末尾有0的除法的特征及计算方法。
二、指导练习
(课件依次出示各题)
1.教学教材第26页练习五第3题。
(1)组织学生看图,理解题意,明确已知条件和所求问题。
已知:全价票每张206元。
问题:求半价票每张多少钱。
(2)师:这里的半价票是什么意思?(点名学生回答)
引导学生明确:半价票的价格是全价票的价格的一半,求半价票的价格用除法计算,列式为206÷2。(板书算式)
(3)组织学生独立笔算,点名学生板演。教师根据学生板演总结商中间有0的除法特征。
师生共同小结:三位数除以一位数,当被除数百位刚好被除数整除,十位上是0时,这样的三位数通常商中间会出现0。(课件出示小结)
2.教学教材第26页练习五第4题。
(1)引导学生明确:“今年一共设了816个人工鸟巢,是去年的4倍”,求“去年设了多少个人工鸟巢”,用除法计算,列式为816÷4。(板书算式)
组织学生独立笔算,互相订正笔算过程及结果。
(2)师:被除数十位上的商是几?(点名学生回答)
师:这类商中间有0的除法有什么特征?应该怎样计算?(小组交流讨论,点名小组代表回答,教师点评总结)
师生共同小结:三位数除以一位数,当被除数的十位不够商“1”时,要商“0”占位,余下的数和个位上的数合起来继续除。(课件出示小结)
3.教学教材第27页练习五第5题。
(1)组织学生独立完成笔算,点名学生说一说哪些除法算式的商中间有0,哪些除法算式的商末尾有0。
(2)师:后面四个除法算式都有余数,对于有余数的除法,我们应该养成验算的习惯。你知道应该怎样验算吗?(点名学生回答)
引导学生明确:对于有余数的除法可以用“除数×商+余数=被除数”来进行验算。
组织学生完成验算。
4.教学教材第27页练习五第8题。
(1)引导学生明确:求“汽车每小时行驶的距离是人步行的多少倍”用除法计算,列式为110÷5。(板书算式)
组织学生笔算,点名学生汇报,并根据学生计算结果板书答案。
师:商的末尾为什么不是0?(点名学生回答)
师:被除数百位上的数小于除数,看被除数的前两位,11÷5=2……1,余数1和个位上的0合并成10,10÷5=2,所以商的末尾是2不是0。
(2)引导学生明确:求“飞机每小时飞行的距离是人步行的多少倍”用除法计算,列式为950÷5。(板书算式)
组织学生笔算,点名学生汇报,并根据学生计算结果板书答案。
师:这里商的末尾为什么是0?(点名学生回答)
三、巩固练习
完成教材第27~28页“练习五”第6、7、10、11、13题。(点名学生板演第6题,学生独立完成第7、10、11、13题,集体订正)
第6题:都错误,改正如下:
第7题:520÷5=104(把)
520÷8=65(把)
第10题:134……1 125……2 280 421(竖式,验算略)
第11题:略
第13题:30
四、课堂小结
通过本堂练习课,你有什么收获?
板书设计
练习课
3.206÷2=103(元)
答:半价票每张103元。
4.816÷4=204(个)
答:去年设了204个人工鸟巢。
8.(1)110÷5=22
答:汽车每小时行驶的距离是人步行的22倍。
(2)950÷5=190
答:飞机每小时飞行的距离是人步行的190倍。
教学反思
1.本课时是练习课,是对前几个课时的巩固,练习的目的是希望学生进一步了解商中出现0的情况。针对性练习提高了学生自主参与探索商中0的位置的积极性,也强化了学生对相关知识的理解和运用能力,充分发挥了练习课的巩固作用。
2.通过练习,也可以发现学生存在的一些问题,比如:有些学生读题能力不强,归纳分析的能力也有所欠缺,需要教师在课堂中多让学生进行这方面的练习,再进行指正,而不是直接将答案公之于众。通过“练习—归纳”“归纳—练习和演绎”的过程,让学生既能灵活运用知识,又能提高归纳能力。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】要使4□□÷3的商的末尾是0,被除数可能是多少?
分析:要使商的末尾是0,则除到被除数的十位正好除尽,且个位上的数字比3小。所以个位上的数字可能是0、1、2,十位上的数字可能是2、5、8,所以□□可能是20、21、22、50、51、52、80、81、82。
解答:被除数可能是420、421、422、450、451、452、480、481、482。
解法归纳:根据商末尾有0的除法的特征可确定被除数各数位上的数字,从而确定被除数。
第7课时 估算的应用
课时目标导航
教学导航
一、教学内容
估算的应用。(教材第29~30页例8、例9)
二、教学目标
1.使学生掌握运用估算解决实际问题的方法。
2.使学生学会从多角度思考来解决问题,培养学生灵活运用各种方法解决问题的能力。
3.通过在具体情境中进行除法估算,学会表达估算的思路,形成估算的习惯和意识。
三、重点难点
重点:掌握三位数除以一位数的估算方法,并利用其解决问题。
难点:结合实际情况,灵活应用估算策略解决问题。
教学过程
一、复习引入
1.口算。
60÷3= 250÷5= 180÷9=
1200÷6= 420÷7= 267÷3=
2.一个羽毛球6元,买28个羽毛球大约多少钱?
师:有一些算式我们很难快速口算出准确的结果。在日常生活中,很多时候我们也不需要计算出准确的结果,而只要计算出大约等于多少就行了,这就要求我们会估算。我们已经学过了三位数加、减法的估算和两位数乘一位数的估算,今天我们继续学习除法估算的问题。(板书课题:估算的应用)
二、学习新课
1.教学教材第29页例8。
(课件出示教材第29页例8)
组织学生看图,理解题意,说一说已知条件和所求问题分别是什么。
师:这里的“大约”是什么意思?(点名学生回答)
引导学生明确:“大约”表示估算,不需要准确计算出每天的住宿费,因此计算结果不能用“=”而只能用“≈”连接。根据“每天的住宿费=总钱数÷住的天数”列式计算。
教师板书:267÷3≈________(元)。
(1)探究估算的方法。
师:要使计算简单,我们可以估算成接近的整百数或几百几十数除以一位数。这道算式中,你准备把267看成哪个数来计算呢?(小组交流讨论,点名小组代表回答,教师板书)
方法一:把267看作与它接近的整百数:300。
267÷3≈100(元)
?
300
方法二:把267看作与它接近的几百几十数:270。
267÷3≈90(元)
?
270
(2)体会估算方法的合理性。
师:我们可以看到,两种方法估算出来的结果并不一样,那么这两种估算方法都合理吗?(小组交流讨论,点名小组代表回答)
引导学生明确:两种估算方法都是正确的,虽然估算出来的结果存在差异,但这种差异在这个问题中是可以忽略不计的。
师:你能通过上面的估算结果判断每天的住宿费比90元多还是比90元少吗?比80元呢?(点名学生回答)
引导学生明确:将267看成270,估算出来的结果是每天的住宿费是90元,被除数变大了,所以商也变大了,所以每天的住宿费比90元少。因为80×3=240<267,所以每天的住宿费比80元多。
教师小结:估算除数是一位数的除法,除数不变,把被除数看成能被整除的整十(百)数或几百几十(几千几百)数,再用口算除法的方法进行计算。(课件出示小结)
2.教学教材第30页例9。
(课件出示教材第30页例9)
组织学生看图,理解题意,说一说已知条件和所求问题分别是什么。
师:“够装”是什么意思?(点名学生回答)
引导学生明确:“够装”是指18个纸箱能装下的菠萝的个数不能少于所摘菠萝的总个数。
师:那么18个纸箱够装吗?需要先算出18个纸箱能装下的菠萝个数吗?(点名学生回答)
(1)探究估算的方法。
师:这个问题,可以用估一估的方法来解决。可以算算18个纸箱大约能装下多少个菠萝,还可以算算182个菠萝大约需要多少个纸箱。你能用这两种方法求解吗?(点名学生回答,教师板书)
方法一:18≈20,20×8=160(个),182>160,18个纸箱不够装。
方法二:182≈180,180÷8>20,18个纸箱不够装。
(2)检验估算结果的正确性。
师:到底需要多少个纸箱才能装下呢?这个问题应该如何解决?(组织小组讨论,独立计算,点名汇报)
引导学生用除法计算,根据计算可得,182除以8得22还余6,说明装了22个纸箱后,还剩6个,所以需要23个纸箱。因此18个纸箱不够,上面的估算方法是合理的。
三、巩固反馈
1.估算。(点名学生回答,并说一说自己的估算方法,集体订正)
640÷7≈90 231÷6≈40 469÷8≈60
176÷9≈20 146÷3≈50 330÷4≈80
2.书店买进了725本书,现在共有9个书架,每个书架可以放78本书,够放吗?(小组交流讨论,点名小组代表回答,集体订正)
78≈80 80×9=720(本)
720<725,不够放。
四、课堂小结
通过本节课的学习,你对估算的应用还有哪些疑问?
板书设计
估算的应用
教学反思
1.除法的估算和以前的四舍五入的估法有一些区别,以前的估算以乘法为主,借助乘法口诀或者整十整百数容易计算的特点,将其中的乘数估成比较接近的整十整百数再进行计算,如49×8,将49估成离它最近的整十数50,然后再计算50×8=400。但是除法的估算不能只考虑与被除数比较接近的整十或整百数,还有整除与否的关系,如401÷7,如果按照乘法估算的原则估成接近的整百数,那就得将401估成400,再计算400÷7,可是根据具体的情况看,400÷7不能整除,这样估算的结果并不简便,估算的意义也就不大了。再比如500÷7,500本身就是个整百数,按照以前估算的方法就不用再估了,可是500并不能被7整除,所以要将500估成490,再计算490÷7=70。因此,在除法估算的教学中,一定要把握好两个原则:一是要比较接近被除数;二是要能够整除。只有同时满足这两个条件,除法的估算才能顺利进行,才能体现出估算的意义。
2.本节课教学的目的不是单纯地教会学生如何去估算,而是要培养学生的估算意识,使不同的算法、算理和谐地统一在解决同一个问题的过程中,使学生在解决同一个问题时会选用不同的计算方法。
3.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】5名教师带领233名学生去划船,每条船限坐8人,大约需要租多少条船?
分析:先用“5+233”求出总人数,然后根据每条船最多可坐8个人,求一共需要多少条船,即求总人数里面有几个8,根据求一个数里面有几个另一个数,用除法解答。
解答:233+5=238(人)
238÷8≈30(条)
答:大约需要租30条船。
相关知识阅读
草船借箭
三国时期,曹操率大军想要征服东吴,孙权、刘备联合抗曹。孙权手下有位大将叫周瑜,智勇双全,可是心胸狭窄,很妒忌诸葛亮的才干。因水中交战需要箭,周瑜要诸葛亮在十天内负责赶造十万支箭,哪知诸葛亮只要三天,还愿立下军令状,完不成任务甘受处罚。周瑜想,三天不可能造出十万支箭,正好利用这个机会来除掉诸葛亮。于是他一面叫军匠们不要把造箭的材料准备齐全,另一方面叫大臣鲁肃去探听诸葛亮的虚实。 鲁肃见了诸葛亮。诸葛亮说:“这件事要请你帮我的忙。希望你能借给我20只船,每只船上30个军士,船要用青布幔子遮起来,还要一千多个草把子,排在船两边。不过,这事千万不能让周瑜知道。” 鲁肃答应了,并按诸葛亮的要求把东西准备齐全。两天过去了,不见一点动静,到第三天四更时,诸葛亮秘密地请鲁肃一起到船上去,说是一起去取箭。鲁肃很纳闷。 诸葛亮吩咐把船用绳索连起来向对岸开去。 那天江上大雾迷漫,对面都看不见人。当船靠近曹军水寨时,诸葛亮命船一字摆开,叫士兵擂鼓呐喊。曹操以为对方来进攻,又因雾大怕中埋伏,就从旱寨派六千名弓箭手朝江中放箭,雨点般的箭纷纷射在草把子上。过了一会儿,诸葛亮又命船掉过头来,让另一面受箭。 太阳出来了,雾要散了,诸葛亮令船赶紧往回开。此时顺风顺水,曹操想追也来不及了。这时船的两边草把子上密密麻麻地插满了箭,诸葛亮让士兵将其中一只船上的箭拔下来数了数,共5346支。听了士兵的报告,诸葛亮笑了笑,说:“好了,这里的箭够十万支了。”你知道诸葛亮是怎么知道箭够十万支的吗?
第8课时 估算的应用(练习课)
课时目标导航
教学导航
一、教学内容
估算的运用练习。(教材第31~32页练习六第3、5、7题)
二、教学目标
1.使学生了解估算在日常生活中的重要性,进一步掌握除法估算的方法,提高学生的估算意识和能力。
2.通过练习,进一步提高学生的估算能力。
3.在练习的过程中培养学生勇于探索、敢于发现问题的精神。
三、重点难点
重点:掌握估算方法,能正确进行估算。
难点:能联系生活实际,灵活运用估算方法。
教学过程
一、基础练习
估算。
87÷9≈ 152÷8≈ 344÷7≈
175÷6≈ 134÷5≈ 273÷4≈
二、指导练习
(课件依次出示各题)
1.教学教材第31页练习六第3题。
组织学生看图,理解题意,找出已知条件和所求问题,说一说如何列式计算。
根据学生回答,板书算式:148÷3。
引导学生将148看成150估算,150是能被3整除的几百几十数,计算简便。
组织学生估算,板书学生估算结果。
师:每件T恤衫实际的售价比50元高还是低?为什么?(点名学生回答)
2.教学教材第32页练习六第5题。
师:两位老师打的字时间不一样,如何比较哪位老师打字打得更快?(点名学生回答)
引导学生根据“打字速度=打字个数÷打字时间”来比较。
师:需要算出两位老师每分钟打字的准确个数吗?(点名学生回答)
师:这里只需要比较大小,因此,我们可以通过估计值来比较。
组织学生估算,点名学生汇报估算方法和结果。根据学生回答,教师板书:
王老师:385÷4≈100(个)
李老师:512÷5≈100(个)
把385看作400是看大了,把512看作500是看小了,所以李老师打字打得更快。
3.教学教材第32页练习六第7题。
组织学生看图,理解题意,明确已知条件和所求问题。
师:如何判断能否把苹果、梨和香蕉都装上车?(小组交流讨论,点名小组代表回答)
学生给出方法:先求出苹果、梨和香蕉的总质量,再与1吨进行比较。
组织学生计算,根据学生计算结果板书:25×9+25×8+25×7=600(千克)。
师:大家还记得1吨等于多少千克吗?(学生齐答)
师:因为600千克小于1000千克,也就是1吨,所以能把苹果、梨和香蕉都装上车。
三、巩固练习
完成教材第31~32页“练习六”第1、2、4、6题。(点名学生回答第1题,给出估算结果和方法,集体订正。学生独立完成第2、4、6题,教师巡视指导,完成后小组间订正并相互交流)
第1题:20 70 30 10 60 70
第2题:255÷4≈60(个)
第4题:(1)128÷6≈20
(2)提问不唯一,例如:比目鱼的寿命大约是青蛙的多少倍?
64÷6≈10
第6题:256÷3≈85(册)
345÷4≈86(册) 478÷5≈96(册)
85<86<96,三年级平均每班捐赠图书的册数最多。
四、课堂小结
通过本节课的练习,你掌握了用估算解决实际问题的方法了吗?
板书设计
估算的应用(练习课)
3.148÷3≈50(元)
答:每件T恤衫大约50元。
5.王老师:385÷4≈100(个)
李老师:512÷5≈100(个)
把385看作400是看大了,把512看作500是看小了,所以李老师打字打得更快。
7.25×9+25×8+25×7=600(千克)
600千克<1吨 把苹果、梨和香蕉都装上车,行。
教学反思
1.估算是小学数学的一个重要内容。教学本节课时,着重抓住两个重要环节。第一,充分利用教材提供的现实情境,努力让学生回想起已有的知识和经验,鼓励学生用自己的方法估算,让学生通过与其他人的合作和交流,互相启发,打开思路,并引导学生进行自我练习,提高估算水平。第二,针对学生对估算把握不好的情况,多给学生独立思考和练习的时间,并适时地给予点拨,帮助学生更好地把握估算。
2.我的补充。
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
备课资料参考
典型例题准备
【例题】在□里填上适当的数,使算式满足条件。
(1)4□1÷2的商大约是200。
(2)□67÷3的商大约是300。
分析:(1)4□1÷2的商大约是200,因为200×2=400,所以4□1是一个接近400的数,根据四舍五入法,十位上的数应该小于5,即□里可以填0、1、2、3、4。
(2)□67÷3的商大约是300,因为300×3=900,被除数十位上的数是6,所以□里应该填8。
解答:(1)□里可以填0、1、2、3、4
(2)□里填8
解法归纳:先用除数和商相乘,求得被除数的估计值,再根据四舍五入法确定□里的数的可能取值。
相关知识阅读
估算的方法
1.去尾法。即把每个数的尾数去掉,取整十数或整百数进行计算。如计算524、208、602、310、219的和,把尾数去掉,取整百数相加,得到524+208+602+310+219≈500+200+600+300+200=1800。
2.进一法。即在每个数的最高位上加1,取整十或整百数进行计算。如28+15+7+24≈30+20+10+30=90。
3.四舍五入法。即尾数小于或等于4的舍去,大于或等于5的则进一,取整十或整百数进行计算。如42×18≈40×20=800。
4.根据部分求整体。即把一个大的整体平均分成若干份,根据部分数求出整体数。如估计体育场内的观众数,先将每个看台平均分成若干份,数一数其中的一份有多少人,然后估计出一个看台的人数,最后根据看台数推算出整个体育场的人数。
