人教版九年级数学下册 27.3.2位似图形的坐标变化规律巩固练习(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学下册 27.3.2位似图形的坐标变化规律巩固练习(Word版 含答案) | 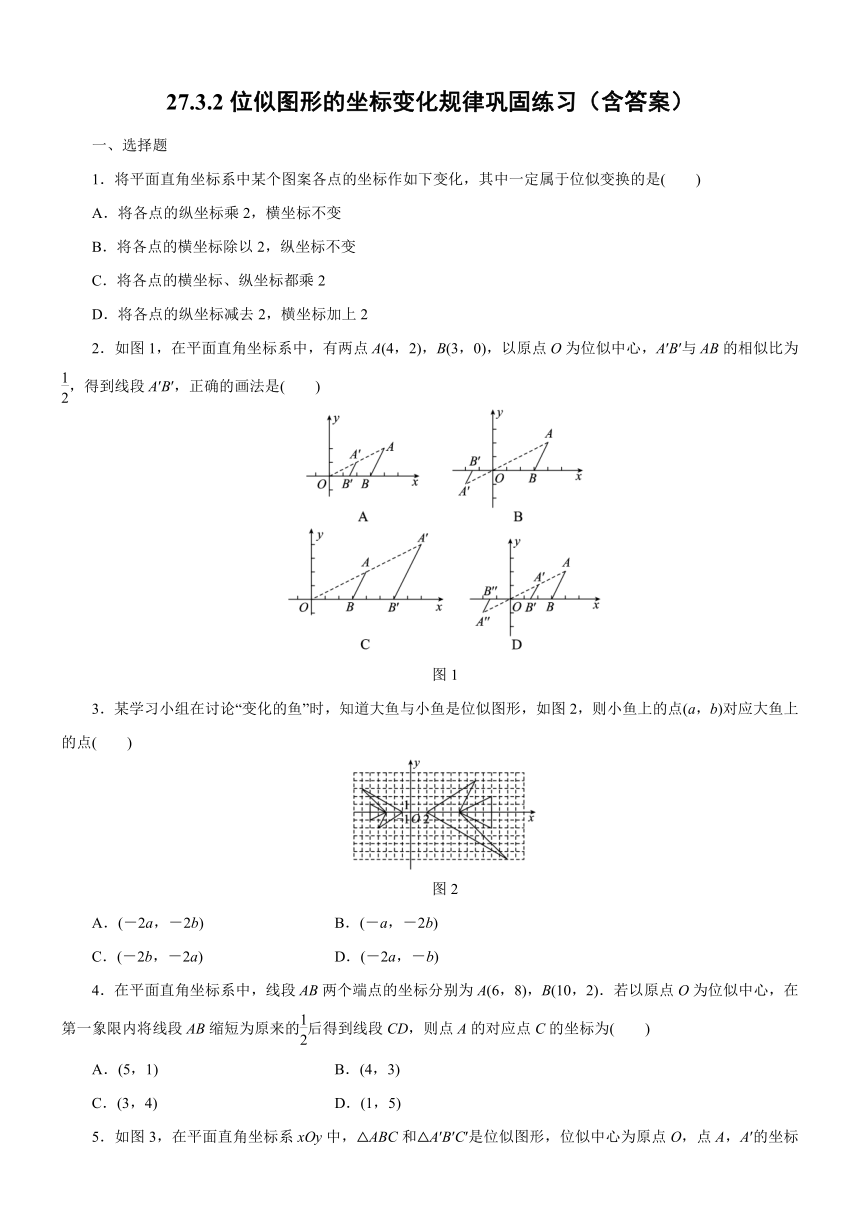 | |
| 格式 | zip | ||
| 文件大小 | 827.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 21:59:55 | ||
图片预览


文档简介
27.3.2位似图形的坐标变化规律巩固练习(含答案)
一、选择题
1.将平面直角坐标系中某个图案各点的坐标作如下变化,其中一定属于位似变换的是( )
A.将各点的纵坐标乘2,横坐标不变
B.将各点的横坐标除以2,纵坐标不变
C.将各点的横坐标、纵坐标都乘2
D.将各点的纵坐标减去2,横坐标加上2
2.如图1,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点O为位似中心,A′B′与AB的相似比为,得到线段A′B′,正确的画法是( )
图1
3.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形,如图2,则小鱼上的点(a,b)对应大鱼上的点( )
图2
A.(-2a,-2b)
B.(-a,-2b)
C.(-2b,-2a)
D.(-2a,-b)
4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2).若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1)
B.(4,3)
C.(3,4)
D.(1,5)
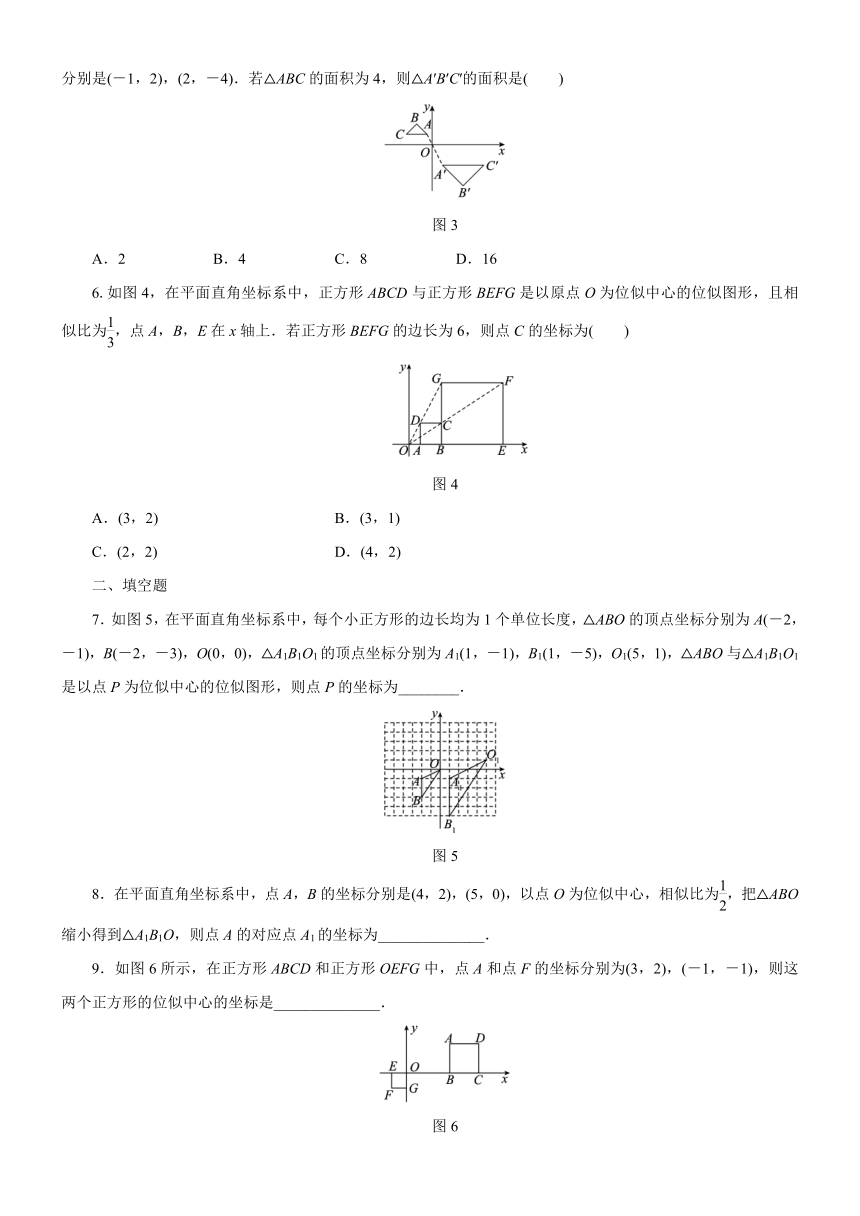
5.如图3,在平面直角坐标系xOy中,△ABC和△A′B′C′是位似图形,位似中心为原点O,点A,A′的坐标分别是(-1,2),(2,-4).若△ABC的面积为4,则△A′B′C′的面积是( )
图3
A.2
B.4
C.8
D.16
6.如图4,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形BEFG的边长为6,则点C的坐标为( )
图4
A.(3,2)
B.(3,1)
C.(2,2)
D.(4,2)
二、填空题
7.如图5,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则点P的坐标为________.
图5
8.在平面直角坐标系中,点A,B的坐标分别是(4,2),(5,0),以点O为位似中心,相似比为,把△ABO缩小得到△A1B1O,则点A的对应点A1的坐标为______________.
9.如图6所示,在正方形ABCD和正方形OEFG中,点A和点F的坐标分别为(3,2),(-1,-1),则这两个正方形的位似中心的坐标是______________.
图6
10.如图7,A是反比例函数y=(x>0)图象上的一点,点B,D在y轴正半轴上,△ABD和△COD是以点D为位似中心的位似图形,且相似比是1∶3,△ABD的面积为1,则k的值为________.
图7
三、解答题
11.如图8,在平面直角坐标系中,依次连接点O(0,0),A(2,2),B(5,2),C(3,0)组成一个图形,请你以原点为位似中心在第一象限内把它放大,使放大前后对应线段的比是1∶4.
图8
12.如图9,在边长均为1的小正方形组成的网格中建立平面直角坐标系,已知△ABC的三个顶点分别为A(-1,2),B(2,1),C(4,5).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC是位似图形,且相似比为2,并求出△A2B2C2的面积.
图9
13.如图10,在平面直角坐标系中,将A(1,0),B(0,2),C(2,3),D(3,1)用线段依次连接起来形成一个图案(图案①).请按要求对图案作如下变换:
(1)将图案①绕点O逆时针旋转90°得到图案②;
(2)以点O为位似中心,相似比为2∶1,将图案①在位似中心的异侧进行放大得到图案③,画出图案③,则变换后点C对应点的坐标为________.
图10
附加题
数形结合在平面直角坐标系中,把一个图形先绕着原点顺时针旋转,旋转角度为θ(0°<θ<360°),再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图11中的△ABC先绕着原点O顺时针旋转90°,再以原点O为位似中心,相似比为得到一个新的图形△A1B1C1,可以把这个过程记为【90°,】变换.
(1)在图中画出一个符合题目要求的△A1B1C1;
(2)若△OMN的顶点坐标分别为O(0,0),M(2,4),N(6,2),把△OMN经过【θ,k】变换后得到△OM′N′,若点M的对应点M′的坐标为(-1,-2),则θ=________,k=________.
图11
参考答案
1.C
2.D [解析]
因为正确的画法有两种情形,故选项D符合要求.
[点评]
注意位似中心、相似比虽然相同,但其位似图形有两种情形.
3.A
4.C [解析]
根据题意,得点C的坐标为(6×,8×),即C(3,4).
5.D [解析]
∵△ABC和△A′B′C′是位似图形,位似中心为原点O,点A,A′的坐标分别是(-1,2),(2,-4),
∴△ABC和△A′B′C′的相似比为1∶2.
∵△ABC的面积为4,
∴△A′B′C′的面积是16.
6.A [解析]
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,∴=,=.
∵BG=6,∴AD=BC=AB=2,
∴=,解得OA=1,
∴OB=3,
∴点C的坐标为(3,2).
7.(-5,-1)
8.(2,1)或(-2,-1)
9.(1,0)或(-5,-2) [解析]
位似中心可以在两个正方形的同侧或异侧.连接AG与BE交于一点,该点可为位似中心,其坐标为(1,0);若连接AE,CG并延长,两线交于一点,该点也可为位似中心,其坐标为(-5,-2).
10.8 [解析]
如图,过点A作AE⊥x轴,垂足为E.
∵△ABD和△COD是以点D为位似中心的位似图形,且相似是1∶3,∴=.
∵OE=AB,
∴==.假设BD=x,AB=y,
∴DO=3x,AE=4x.
∵△ABD的面积为1,
∴xy=1,∴xy=2,
∴AB·AE=4xy=8,即k=4xy=8.
11.解:如图,四边形OA′B′C′就是所要求的图形.
12.解:(1)如图所示,△A1B1C1就是所要求的三角形.
(2)如图所示,△A2B2C2就是所要求的三角形.
如图,分别过点A2,C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E,F,
∵A(-1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,位似中心为原点O,且相似比为2,
∴A2(-2,4),B2(4,2),C2(8,10),
∴A2E=2,C2F=8,EF=10,B2E=6,B2F=4,
∴S△A2B2C2=×(2+8)×10-×2×6-×4×8=28.
13.解:(1)图案②如图所示.
(2)图案③如图所示,变换后点C对应点的坐标为(-4,-6).
附加题
解:(1)答案不唯一,如图所示.
(2)由于M(2,4),M′(-1,-2)都在直线y=2x上,
即M,O,M′三点共线,由0°<θ<360°,得θ=180°.
根据M,M′的坐标易知OM=2OM′,即k=.
故θ=180°,k=.
一、选择题
1.将平面直角坐标系中某个图案各点的坐标作如下变化,其中一定属于位似变换的是( )
A.将各点的纵坐标乘2,横坐标不变
B.将各点的横坐标除以2,纵坐标不变
C.将各点的横坐标、纵坐标都乘2
D.将各点的纵坐标减去2,横坐标加上2
2.如图1,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点O为位似中心,A′B′与AB的相似比为,得到线段A′B′,正确的画法是( )
图1
3.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形,如图2,则小鱼上的点(a,b)对应大鱼上的点( )
图2
A.(-2a,-2b)
B.(-a,-2b)
C.(-2b,-2a)
D.(-2a,-b)
4.在平面直角坐标系中,线段AB两个端点的坐标分别为A(6,8),B(10,2).若以原点O为位似中心,在第一象限内将线段AB缩短为原来的后得到线段CD,则点A的对应点C的坐标为( )
A.(5,1)
B.(4,3)
C.(3,4)
D.(1,5)
5.如图3,在平面直角坐标系xOy中,△ABC和△A′B′C′是位似图形,位似中心为原点O,点A,A′的坐标分别是(-1,2),(2,-4).若△ABC的面积为4,则△A′B′C′的面积是( )
图3
A.2
B.4
C.8
D.16
6.如图4,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,点A,B,E在x轴上.若正方形BEFG的边长为6,则点C的坐标为( )
图4
A.(3,2)
B.(3,1)
C.(2,2)
D.(4,2)
二、填空题
7.如图5,在平面直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则点P的坐标为________.
图5
8.在平面直角坐标系中,点A,B的坐标分别是(4,2),(5,0),以点O为位似中心,相似比为,把△ABO缩小得到△A1B1O,则点A的对应点A1的坐标为______________.
9.如图6所示,在正方形ABCD和正方形OEFG中,点A和点F的坐标分别为(3,2),(-1,-1),则这两个正方形的位似中心的坐标是______________.
图6
10.如图7,A是反比例函数y=(x>0)图象上的一点,点B,D在y轴正半轴上,△ABD和△COD是以点D为位似中心的位似图形,且相似比是1∶3,△ABD的面积为1,则k的值为________.
图7
三、解答题
11.如图8,在平面直角坐标系中,依次连接点O(0,0),A(2,2),B(5,2),C(3,0)组成一个图形,请你以原点为位似中心在第一象限内把它放大,使放大前后对应线段的比是1∶4.
图8
12.如图9,在边长均为1的小正方形组成的网格中建立平面直角坐标系,已知△ABC的三个顶点分别为A(-1,2),B(2,1),C(4,5).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC是位似图形,且相似比为2,并求出△A2B2C2的面积.
图9
13.如图10,在平面直角坐标系中,将A(1,0),B(0,2),C(2,3),D(3,1)用线段依次连接起来形成一个图案(图案①).请按要求对图案作如下变换:
(1)将图案①绕点O逆时针旋转90°得到图案②;
(2)以点O为位似中心,相似比为2∶1,将图案①在位似中心的异侧进行放大得到图案③,画出图案③,则变换后点C对应点的坐标为________.
图10
附加题
数形结合在平面直角坐标系中,把一个图形先绕着原点顺时针旋转,旋转角度为θ(0°<θ<360°),再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图11中的△ABC先绕着原点O顺时针旋转90°,再以原点O为位似中心,相似比为得到一个新的图形△A1B1C1,可以把这个过程记为【90°,】变换.
(1)在图中画出一个符合题目要求的△A1B1C1;
(2)若△OMN的顶点坐标分别为O(0,0),M(2,4),N(6,2),把△OMN经过【θ,k】变换后得到△OM′N′,若点M的对应点M′的坐标为(-1,-2),则θ=________,k=________.
图11
参考答案
1.C
2.D [解析]
因为正确的画法有两种情形,故选项D符合要求.
[点评]
注意位似中心、相似比虽然相同,但其位似图形有两种情形.
3.A
4.C [解析]
根据题意,得点C的坐标为(6×,8×),即C(3,4).
5.D [解析]
∵△ABC和△A′B′C′是位似图形,位似中心为原点O,点A,A′的坐标分别是(-1,2),(2,-4),
∴△ABC和△A′B′C′的相似比为1∶2.
∵△ABC的面积为4,
∴△A′B′C′的面积是16.
6.A [解析]
∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为,∴=,=.
∵BG=6,∴AD=BC=AB=2,
∴=,解得OA=1,
∴OB=3,
∴点C的坐标为(3,2).
7.(-5,-1)
8.(2,1)或(-2,-1)
9.(1,0)或(-5,-2) [解析]
位似中心可以在两个正方形的同侧或异侧.连接AG与BE交于一点,该点可为位似中心,其坐标为(1,0);若连接AE,CG并延长,两线交于一点,该点也可为位似中心,其坐标为(-5,-2).
10.8 [解析]
如图,过点A作AE⊥x轴,垂足为E.
∵△ABD和△COD是以点D为位似中心的位似图形,且相似是1∶3,∴=.
∵OE=AB,
∴==.假设BD=x,AB=y,
∴DO=3x,AE=4x.
∵△ABD的面积为1,
∴xy=1,∴xy=2,
∴AB·AE=4xy=8,即k=4xy=8.
11.解:如图,四边形OA′B′C′就是所要求的图形.
12.解:(1)如图所示,△A1B1C1就是所要求的三角形.
(2)如图所示,△A2B2C2就是所要求的三角形.
如图,分别过点A2,C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E,F,
∵A(-1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,位似中心为原点O,且相似比为2,
∴A2(-2,4),B2(4,2),C2(8,10),
∴A2E=2,C2F=8,EF=10,B2E=6,B2F=4,
∴S△A2B2C2=×(2+8)×10-×2×6-×4×8=28.
13.解:(1)图案②如图所示.
(2)图案③如图所示,变换后点C对应点的坐标为(-4,-6).
附加题
解:(1)答案不唯一,如图所示.
(2)由于M(2,4),M′(-1,-2)都在直线y=2x上,
即M,O,M′三点共线,由0°<θ<360°,得θ=180°.
根据M,M′的坐标易知OM=2OM′,即k=.
故θ=180°,k=.
