苏科版八年级上册 6.4 用一次函数解决问题(图像综合)选择题拔高训练(二)(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册 6.4 用一次函数解决问题(图像综合)选择题拔高训练(二)(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 22:05:12 | ||
图片预览

文档简介
第六章
一次函数应用(图像综合)
选择题拔高训练(二)
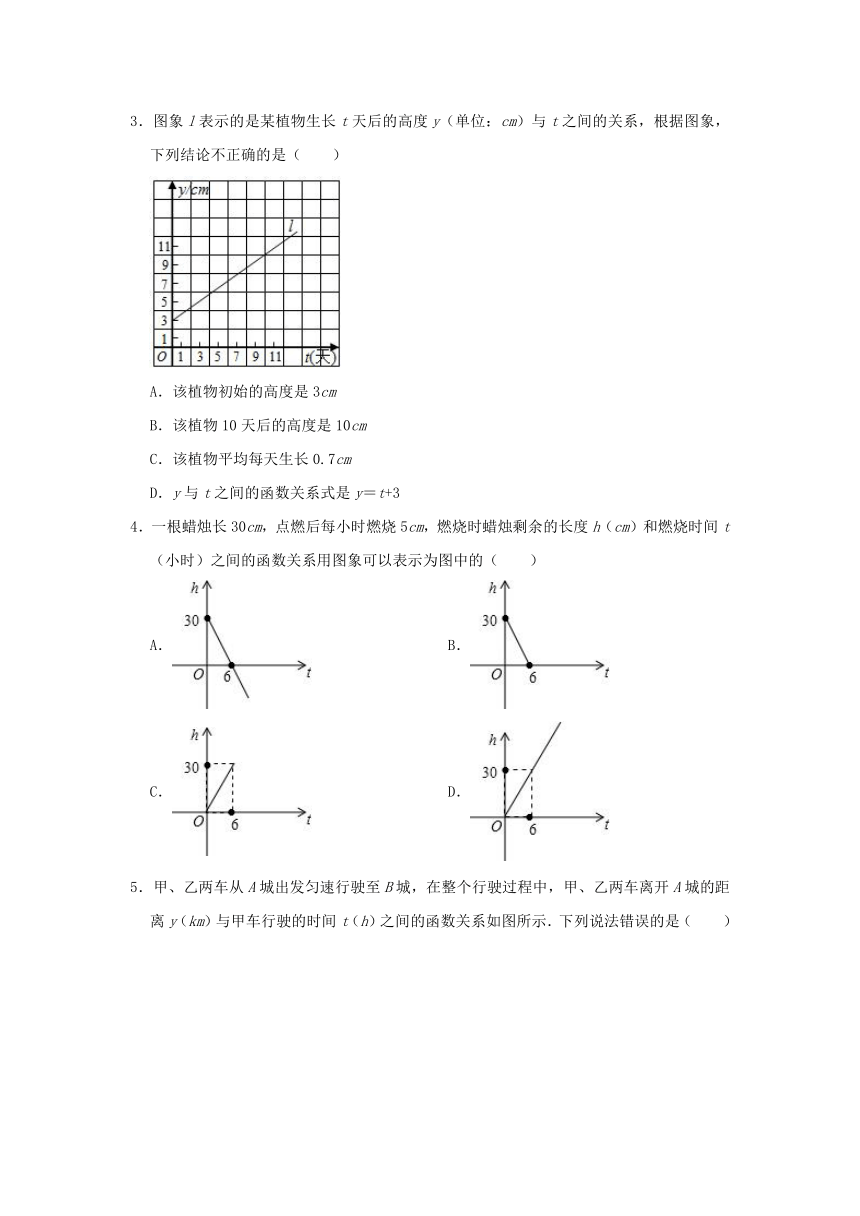
1.某校八年级同学到距学校8千米的某地参加社会实践活动,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,a,b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象.则下列判断错误的是( )
A.骑车的同学比步行的同学晚出发30分钟
B.骑车的同学和步行的同学同时到达目的地
C.步行的速度是7.5千米/小时
D.骑车的同学从出发到追上步行的同学用了18分钟
2.若A、B两地的距离是120km,甲和乙沿相同的路线由A地到B地的行驶路程与时间的关系如图所示.根据图象判断以下结论正确的个数有( )
①甲比乙晚两小时出发
②甲的速度是30km/h,乙的速度是15km/h
③乙出发4小时后,甲在乙的前面
④甲行驶的路程y与时间x的函数关系是y=15x
A.1个
B.2个
C.3个
D.4个
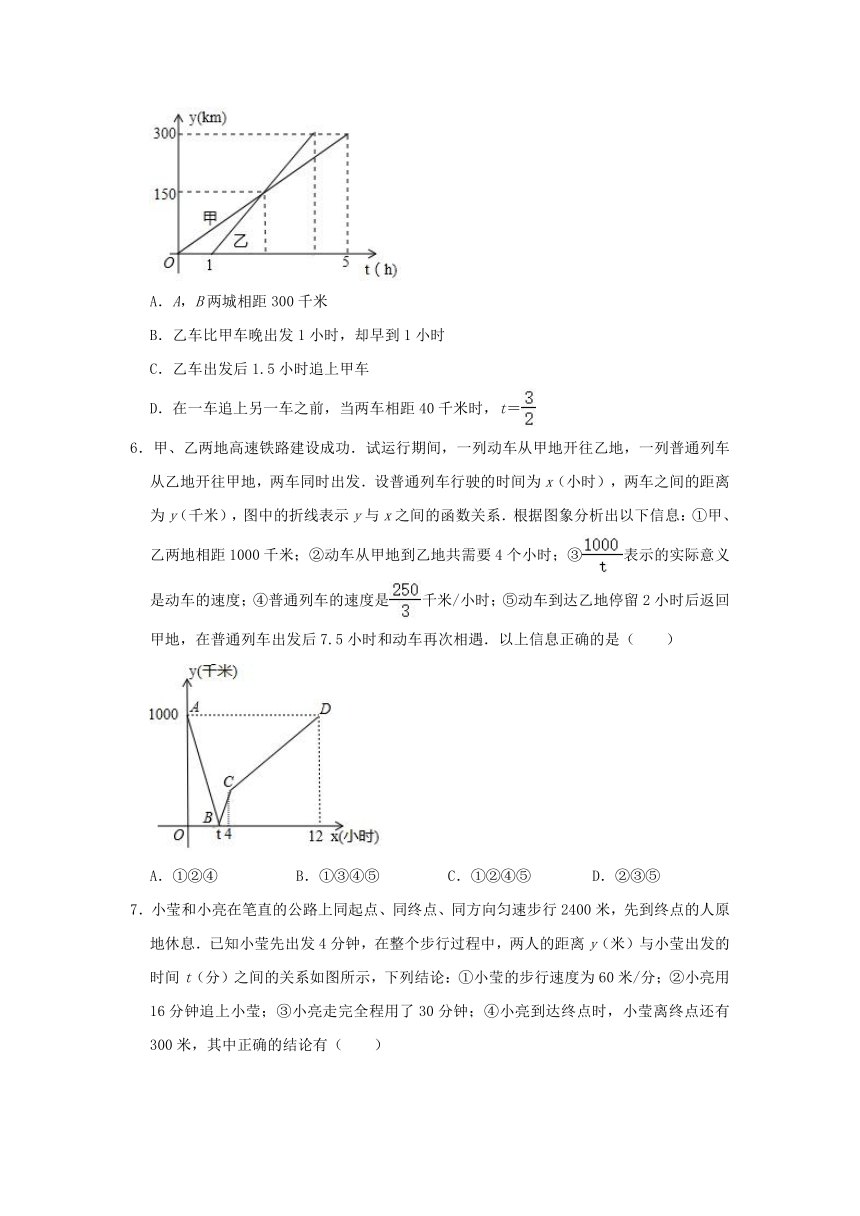
3.图象l表示的是某植物生长t天后的高度y(单位:cm)与t之间的关系,根据图象,下列结论不正确的是( )
A.该植物初始的高度是3cm
B.该植物10天后的高度是10cm
C.该植物平均每天生长0.7cm
D.y与t之间的函数关系式是y=t+3
4.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( )
A.
B.
C.
D.
5.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.下列说法错误的是( )
A.A,B两城相距300千米
B.乙车比甲车晚出发1小时,却早到1小时
C.乙车出发后1.5小时追上甲车
D.在一车追上另一车之前,当两车相距40千米时,t=
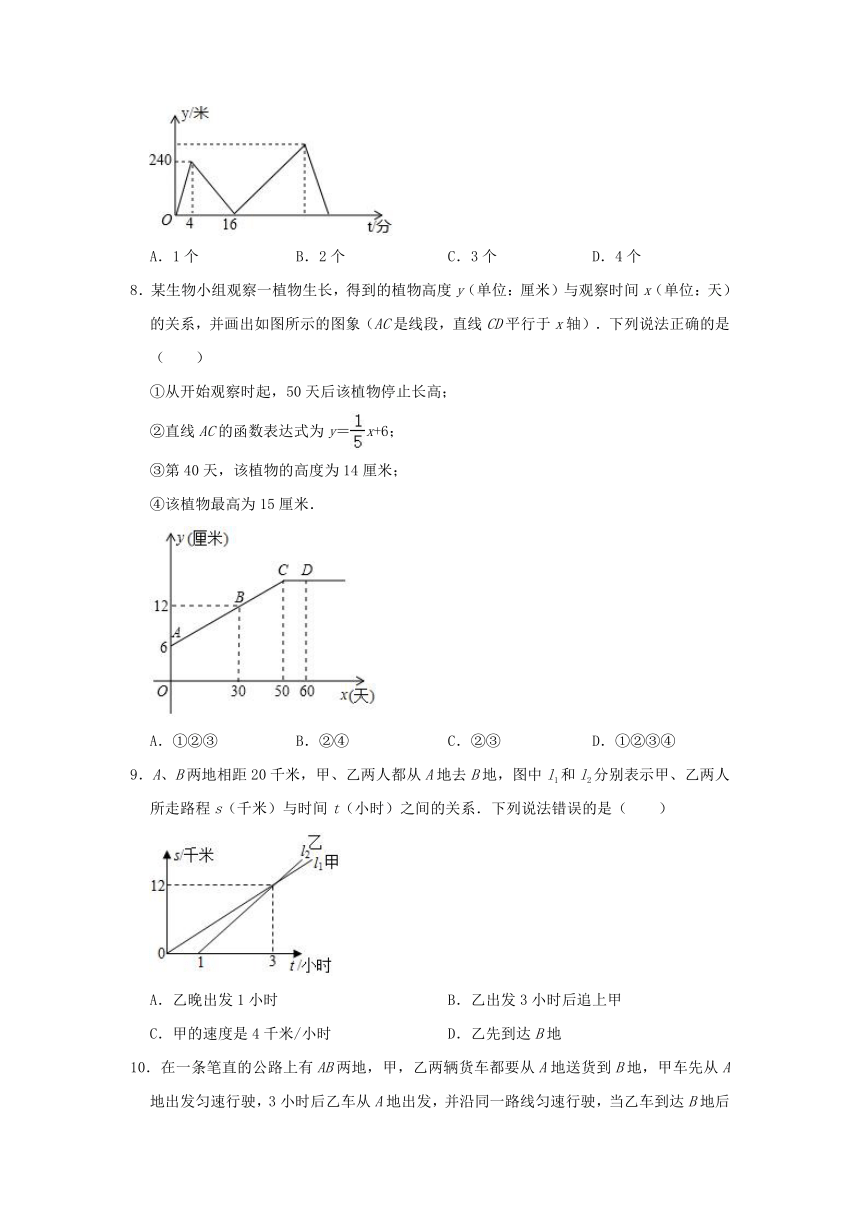
6.甲、乙两地高速铁路建设成功.试运行期间,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系.根据图象分析出以下信息:①甲、乙两地相距1000千米;②动车从甲地到乙地共需要4个小时;③表示的实际意义是动车的速度;④普通列车的速度是千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
A.①②④
B.①③④⑤
C.①②④⑤
D.②③⑤
7.小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知小莹先出发4分钟,在整个步行过程中,两人的距离y(米)与小莹出发的时间t(分)之间的关系如图所示,下列结论:①小莹的步行速度为60米/分;②小亮用16分钟追上小莹;③小亮走完全程用了30分钟;④小亮到达终点时,小莹离终点还有300米,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
8.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( )
①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③
B.②④
C.②③
D.①②③④
9.A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.下列说法错误的是( )
A.乙晚出发1小时
B.乙出发3小时后追上甲
C.甲的速度是4千米/小时
D.乙先到达B地
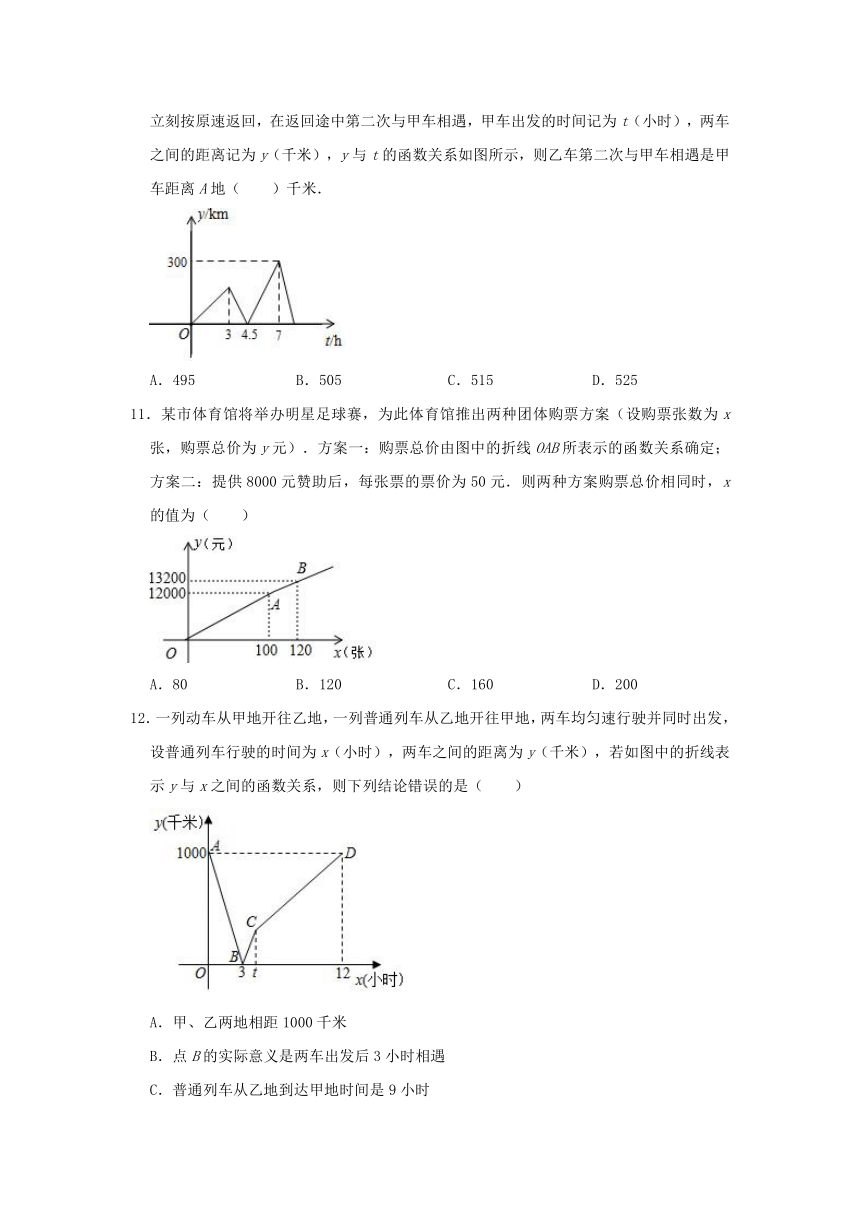
10.在一条笔直的公路上有AB两地,甲,乙两辆货车都要从A地送货到B地,甲车先从A地出发匀速行驶,3小时后乙车从A地出发,并沿同一路线匀速行驶,当乙车到达B地后立刻按原速返回,在返回途中第二次与甲车相遇,甲车出发的时间记为t(小时),两车之间的距离记为y(千米),y与t的函数关系如图所示,则乙车第二次与甲车相遇是甲车距离A地( )千米.
A.495
B.505
C.515
D.525
11.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为y元).方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为( )
A.80
B.120
C.160
D.200
12.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),若如图中的折线表示y与x之间的函数关系,则下列结论错误的是( )
A.甲、乙两地相距1000千米
B.点B的实际意义是两车出发后3小时相遇
C.普通列车从乙地到达甲地时间是9小时
D.动车的速度是250千米/小时
13.汽车开始行驶时,油箱内有油50升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示应为( )
A.
B.
C.
D.
14.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
15.A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.对于下列说法:
①乙晚出发1小时:②乙出发3小时后追上甲;
③甲的速度是6千米/小时;④乙先到达B地.其中正确的个数是( )
A.4个
B.3个
C.2个
D.1个
16.小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;
②小华的速度是小明速度的2.5倍;
③a=24;
④b=480.
其中正确的是( )
A.①②④
B.①②③
C.①③④
D.①②③④
17.成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s
(千米)与所花时间t
(分钟)之间的函数关系,下列说法错误的是( )
A.他离家8千米,共用了30分钟
B.他等公交车时间为6分钟
C.他步行的速度是100米/分钟
D.公交车的速度是350米/分钟
18.一条公路旁依次有A、B、C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论,其中正确结论的个数是( )
①A、B两村相距8km;
②甲出发2h后到达C村;
③甲每小时比乙多骑行8km;
④相遇后,乙又骑行了15min或45min时两人相距2km.
A.1
B.2
C.3
D.4
19.一辆货车从甲地匀速驶往乙地用了2.7h,到达后用了0.5h卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的1.5倍,货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示,则a等于( )
A.4.7
B.5.0
C.5.4
D.5.8
20.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=30.以上结论正确的有( )
A.①②
B.①②③
C.①③④
D.①②④
参考答案
1.解:骑车的同学比步行的同学晚出发30分钟,所以选项A不合题意;
骑车的同学比步行的同学提前10分钟到达目的地,故本选项符合题意;
步行的速度是8÷=7.5千米/小时,所以选项C不合题意;
设骑车的同学从出发到追上步行的同学用了x分钟,根据题意得:
8÷(54﹣30)x=30×7.5+7.5x,解得x=18,
所以选项D不合题意;
故选:B.
2.解:由图可知,
甲比乙晚两小时出发,故①正确;
甲的速度为:120÷(6﹣2)=120÷4=30km/h,乙的速度为:120÷8=15km/h,故②正确;
乙出发4小时后,甲在乙的前面,故③正确;
设甲行驶的路程y与x的函数关系式为y=kx+b,
,得,
即甲行驶的路程y与x的函数关系式为y=30x﹣60,故④错误;
故选:C.
3.解:对于A,有图象中(0,3)可知植物初始高度是3cm,故A选项正确,不符合题意;
对于B,图象中(10,10)可知植物10天后高度是10,故B选项正确,不符合题意;
对于C,由10天内生长10﹣3=7cm可知,平均每天生长0.7cm,故C选项正确,不符合题意;
对于D,设函数解析式为y=kt+b,将(0,3)和(10,10)代入
,解得.
∴y=0.7t+3.
故D选项错误,符合题意.
故选:D.
4.解:由题意,得
y=30﹣5t,
∵y≥0,t≥0,
∴30﹣5t≥0,
∴t≤6,
∴0≤t≤6,
∴y=30﹣5t是降函数且图象是一条线段.
故选:B.
5.解:由图象可知A、B两城市之间的距离为300km,故A正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得,解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5﹣1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故B正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故C正确;
乙还未出发,甲在时前进了40米,
乙在甲后面40km时,y甲﹣y乙=40,可得60t﹣100t+100=40,解得t=,
即在一车追上另一车之前,当两车相距40千米时,t=或,故D错误.
故选:D.
6.解:由图象可得,
AB两地相距1000千米,故①正确;
由出发4小时后两车的距离增加速度不变并比原来的增加速度变小即可得出动车从甲地到乙地共需要4个小时,故②正确;
表示的实际意义是动车与普通列车的速度和,故③错误;
普通列车的速度是(千米/小时),故④正确;
设动车的速度为x千米/小时,
根据题意,得:3x+3×=1000,
解得:x=250,
动车的速度为250千米/小时,
设动车与普通列车再次相遇时普通列车出发了t小时,根据题意得
,解得t=9,
即动车到达乙地停留2小时后返回甲地,在普通列车出发后9小时和动车再次相遇.故⑤错误.
综上所述,正确的有:①②④.
故选:A.
7.解:由图可得:
小莹步行的速度为:240÷4=60米/分,故①正确,
小亮追上小莹用的时间为:16﹣4=12(分钟),故②错误,
小亮走完全程用的时间为:2400÷(16×60÷12)=30(分钟),故③正确,
小亮到达终点时,小莹离终点距离是:2400﹣(4+30)×60=360米,故④错误,
故选:B.
8.解:∵CD∥x轴,
∴从第50天开始植物的高度不变,
故①的说法正确;
设直线AC的解析式为y=kx+b(k≠0),
∵经过点A(0,6),B(30,12),
∴,
解得,
所以,直线AC的解析式为y=x+6(0≤x≤50),
故②的结论正确;
当x=40时,y=×40+6=14,
即第40天,该植物的高度为14厘米;
故③的说法正确;
当x=50时,y=×50+6=16,
即第50天,该植物的高度为16厘米;
故④的说法错误.
综上所述,正确的是①②③.
故选:A.
9.解:由图象可得,
乙晚出发1小时,故选项A正确;
乙出发3﹣1=2小时追上甲,故选项B错误;
甲的速度是12÷3=4(千米/小时),故选项C正确;
乙先到达B地,故选项D正确;
故选:B.
10.解:设甲车的速度为akm/h,乙车的速度为bkm/h,
,
解得,,
设甲乙第二次相遇的时间为t小时,
300=(60+180)×(t﹣7),
解得,t=,
则乙车第二次与甲车相遇时,甲车距离A地:60×=495(千米),
故选:A.
11.解:设OA段对应的函数解析式为y=kx,
12000=100k,得k=120,
即OA段对应的函数解析式为y=120x,
设AB段对应的函数解析式为y=ax+b,
,得,
即AB段对应的函数解析式为y=60x+6000,
由题意可得,方案二中y与x的函数关系式为y=50x+8000,
令50x+8000=120x,得x=,
∵x为整数,
∴x=应舍去,
令60x+6000=50x+8000,得x=200,
即当x=200时,两种方案购票总价相同,
故选:D.
12.解:由图象可得,
甲、乙两地相距1000千米,故选项A正确;
点B的实际意义是两车出发后3小时相遇,故选项B正确;
普通列车从乙地到达甲地时间是12小时,故选项C错误;
普通列出的速度为1000÷12=(千米/小时),动车的速度为:1000÷3﹣=250(千米/小时),故选项D正确;
故选:C.
13.解:由题意可得,
Q=50﹣5t,
当t=0时,Q=50,当Q=0时,t=10,
故选:C.
14.解:设y与x的函数关系为y=kx+b,由题意得:
,
解得:,
∴y=5000x+2000,
当x=0时,
y=5000×0+2000=2000,
∴营销人员没有销售量时最低收入是2000元,
故选:B.
15.解:由图可知,
乙晚出发1小时,故①正确;
乙出发3﹣1=2小时后追上甲,故②错误;
甲的速度是:18÷3=6(千米/小时),故③正确;
乙先到达B地,故④正确;
故选:B.
16.解:由图象得出小明步行720米,需要9分钟,
所以小明的运动速度为:720÷9=80(m/分),
当第15分钟时,小华运动15﹣9=6(分钟),
运动距离为:15×80=1200(m),
∴小华的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明小华已经到达终点,则小华先到达青少年宫,(故①正确);
此时小华运动19﹣9=10(分钟),
运动总距离为:10×200=2000(m),
∴小明运动时间为:2000÷80=25(分钟),
故a的值为25,(故③错误);
∵小明19分钟运动距离为:19×80=1520(m),
∴b=2000﹣1520=480,(故④正确).
故正确的有:①②④.
故选:A.
17.解:A、依题意他离家8km共用了30min,故选项正确;
B、依题意在第10min开始等公交车,第16min结束,故他等公交车时间为6min,故选项正确;
C、他步行10min走了1000m,故他步行的速度为他步行的速度是100m/min,故选项正确;
D、公交车(30﹣16)min走了(8﹣1)km,故公交车的速度为7000÷14=500m/min,故选项错误.
故选:D.
18.解:由图可得,
A、B两村相距8km,故①正确;
甲出发1.5h后到达C村,故②错误;
甲每小时比乙多骑行8km,故③正确;
相遇后,乙又骑行了=15min或(1.5﹣1)×60+=45min时两人相距2km,故④正确;
故选:C.
19.解:设甲乙两地的路程为s,从甲地到乙地的速度为v,从乙地到甲地的时间为t,
则
解得,t=1.8
∴a=3.2+1.8=5(小时),
故选:B.
20.解:①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(24﹣4)=60(m/min),
甲的速度为1200÷12﹣60=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②正确;
③b=(60+40)×(24﹣4﹣12)=800,结论③正确;
④a=1200÷40+4=34,结论④错误.
故结论正确的有①②③,
故选:B.
一次函数应用(图像综合)
选择题拔高训练(二)
1.某校八年级同学到距学校8千米的某地参加社会实践活动,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,a,b分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象.则下列判断错误的是( )
A.骑车的同学比步行的同学晚出发30分钟
B.骑车的同学和步行的同学同时到达目的地
C.步行的速度是7.5千米/小时
D.骑车的同学从出发到追上步行的同学用了18分钟
2.若A、B两地的距离是120km,甲和乙沿相同的路线由A地到B地的行驶路程与时间的关系如图所示.根据图象判断以下结论正确的个数有( )
①甲比乙晚两小时出发
②甲的速度是30km/h,乙的速度是15km/h
③乙出发4小时后,甲在乙的前面
④甲行驶的路程y与时间x的函数关系是y=15x
A.1个
B.2个
C.3个
D.4个
3.图象l表示的是某植物生长t天后的高度y(单位:cm)与t之间的关系,根据图象,下列结论不正确的是( )
A.该植物初始的高度是3cm
B.该植物10天后的高度是10cm
C.该植物平均每天生长0.7cm
D.y与t之间的函数关系式是y=t+3
4.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( )
A.
B.
C.
D.
5.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.下列说法错误的是( )
A.A,B两城相距300千米
B.乙车比甲车晚出发1小时,却早到1小时
C.乙车出发后1.5小时追上甲车
D.在一车追上另一车之前,当两车相距40千米时,t=
6.甲、乙两地高速铁路建设成功.试运行期间,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系.根据图象分析出以下信息:①甲、乙两地相距1000千米;②动车从甲地到乙地共需要4个小时;③表示的实际意义是动车的速度;④普通列车的速度是千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
A.①②④
B.①③④⑤
C.①②④⑤
D.②③⑤
7.小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知小莹先出发4分钟,在整个步行过程中,两人的距离y(米)与小莹出发的时间t(分)之间的关系如图所示,下列结论:①小莹的步行速度为60米/分;②小亮用16分钟追上小莹;③小亮走完全程用了30分钟;④小亮到达终点时,小莹离终点还有300米,其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
8.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( )
①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③
B.②④
C.②③
D.①②③④
9.A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.下列说法错误的是( )
A.乙晚出发1小时
B.乙出发3小时后追上甲
C.甲的速度是4千米/小时
D.乙先到达B地
10.在一条笔直的公路上有AB两地,甲,乙两辆货车都要从A地送货到B地,甲车先从A地出发匀速行驶,3小时后乙车从A地出发,并沿同一路线匀速行驶,当乙车到达B地后立刻按原速返回,在返回途中第二次与甲车相遇,甲车出发的时间记为t(小时),两车之间的距离记为y(千米),y与t的函数关系如图所示,则乙车第二次与甲车相遇是甲车距离A地( )千米.
A.495
B.505
C.515
D.525
11.某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为y元).方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为( )
A.80
B.120
C.160
D.200
12.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),若如图中的折线表示y与x之间的函数关系,则下列结论错误的是( )
A.甲、乙两地相距1000千米
B.点B的实际意义是两车出发后3小时相遇
C.普通列车从乙地到达甲地时间是9小时
D.动车的速度是250千米/小时
13.汽车开始行驶时,油箱内有油50升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示应为( )
A.
B.
C.
D.
14.某公司市场营销部的个人收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000
B.2000
C.3000
D.4000
15.A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.对于下列说法:
①乙晚出发1小时:②乙出发3小时后追上甲;
③甲的速度是6千米/小时;④乙先到达B地.其中正确的个数是( )
A.4个
B.3个
C.2个
D.1个
16.小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:
①小华先到达青少年宫;
②小华的速度是小明速度的2.5倍;
③a=24;
④b=480.
其中正确的是( )
A.①②④
B.①②③
C.①③④
D.①②③④
17.成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s
(千米)与所花时间t
(分钟)之间的函数关系,下列说法错误的是( )
A.他离家8千米,共用了30分钟
B.他等公交车时间为6分钟
C.他步行的速度是100米/分钟
D.公交车的速度是350米/分钟
18.一条公路旁依次有A、B、C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论,其中正确结论的个数是( )
①A、B两村相距8km;
②甲出发2h后到达C村;
③甲每小时比乙多骑行8km;
④相遇后,乙又骑行了15min或45min时两人相距2km.
A.1
B.2
C.3
D.4
19.一辆货车从甲地匀速驶往乙地用了2.7h,到达后用了0.5h卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地速度的1.5倍,货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示,则a等于( )
A.4.7
B.5.0
C.5.4
D.5.8
20.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=30.以上结论正确的有( )
A.①②
B.①②③
C.①③④
D.①②④
参考答案
1.解:骑车的同学比步行的同学晚出发30分钟,所以选项A不合题意;
骑车的同学比步行的同学提前10分钟到达目的地,故本选项符合题意;
步行的速度是8÷=7.5千米/小时,所以选项C不合题意;
设骑车的同学从出发到追上步行的同学用了x分钟,根据题意得:
8÷(54﹣30)x=30×7.5+7.5x,解得x=18,
所以选项D不合题意;
故选:B.
2.解:由图可知,
甲比乙晚两小时出发,故①正确;
甲的速度为:120÷(6﹣2)=120÷4=30km/h,乙的速度为:120÷8=15km/h,故②正确;
乙出发4小时后,甲在乙的前面,故③正确;
设甲行驶的路程y与x的函数关系式为y=kx+b,
,得,
即甲行驶的路程y与x的函数关系式为y=30x﹣60,故④错误;
故选:C.
3.解:对于A,有图象中(0,3)可知植物初始高度是3cm,故A选项正确,不符合题意;
对于B,图象中(10,10)可知植物10天后高度是10,故B选项正确,不符合题意;
对于C,由10天内生长10﹣3=7cm可知,平均每天生长0.7cm,故C选项正确,不符合题意;
对于D,设函数解析式为y=kt+b,将(0,3)和(10,10)代入
,解得.
∴y=0.7t+3.
故D选项错误,符合题意.
故选:D.
4.解:由题意,得
y=30﹣5t,
∵y≥0,t≥0,
∴30﹣5t≥0,
∴t≤6,
∴0≤t≤6,
∴y=30﹣5t是降函数且图象是一条线段.
故选:B.
5.解:由图象可知A、B两城市之间的距离为300km,故A正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得,解得,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
乙的速度:150÷(2.5﹣1)=100,
乙的时间:300÷100=3,
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故B正确;
甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故C正确;
乙还未出发,甲在时前进了40米,
乙在甲后面40km时,y甲﹣y乙=40,可得60t﹣100t+100=40,解得t=,
即在一车追上另一车之前,当两车相距40千米时,t=或,故D错误.
故选:D.
6.解:由图象可得,
AB两地相距1000千米,故①正确;
由出发4小时后两车的距离增加速度不变并比原来的增加速度变小即可得出动车从甲地到乙地共需要4个小时,故②正确;
表示的实际意义是动车与普通列车的速度和,故③错误;
普通列车的速度是(千米/小时),故④正确;
设动车的速度为x千米/小时,
根据题意,得:3x+3×=1000,
解得:x=250,
动车的速度为250千米/小时,
设动车与普通列车再次相遇时普通列车出发了t小时,根据题意得
,解得t=9,
即动车到达乙地停留2小时后返回甲地,在普通列车出发后9小时和动车再次相遇.故⑤错误.
综上所述,正确的有:①②④.
故选:A.
7.解:由图可得:
小莹步行的速度为:240÷4=60米/分,故①正确,
小亮追上小莹用的时间为:16﹣4=12(分钟),故②错误,
小亮走完全程用的时间为:2400÷(16×60÷12)=30(分钟),故③正确,
小亮到达终点时,小莹离终点距离是:2400﹣(4+30)×60=360米,故④错误,
故选:B.
8.解:∵CD∥x轴,
∴从第50天开始植物的高度不变,
故①的说法正确;
设直线AC的解析式为y=kx+b(k≠0),
∵经过点A(0,6),B(30,12),
∴,
解得,
所以,直线AC的解析式为y=x+6(0≤x≤50),
故②的结论正确;
当x=40时,y=×40+6=14,
即第40天,该植物的高度为14厘米;
故③的说法正确;
当x=50时,y=×50+6=16,
即第50天,该植物的高度为16厘米;
故④的说法错误.
综上所述,正确的是①②③.
故选:A.
9.解:由图象可得,
乙晚出发1小时,故选项A正确;
乙出发3﹣1=2小时追上甲,故选项B错误;
甲的速度是12÷3=4(千米/小时),故选项C正确;
乙先到达B地,故选项D正确;
故选:B.
10.解:设甲车的速度为akm/h,乙车的速度为bkm/h,
,
解得,,
设甲乙第二次相遇的时间为t小时,
300=(60+180)×(t﹣7),
解得,t=,
则乙车第二次与甲车相遇时,甲车距离A地:60×=495(千米),
故选:A.
11.解:设OA段对应的函数解析式为y=kx,
12000=100k,得k=120,
即OA段对应的函数解析式为y=120x,
设AB段对应的函数解析式为y=ax+b,
,得,
即AB段对应的函数解析式为y=60x+6000,
由题意可得,方案二中y与x的函数关系式为y=50x+8000,
令50x+8000=120x,得x=,
∵x为整数,
∴x=应舍去,
令60x+6000=50x+8000,得x=200,
即当x=200时,两种方案购票总价相同,
故选:D.
12.解:由图象可得,
甲、乙两地相距1000千米,故选项A正确;
点B的实际意义是两车出发后3小时相遇,故选项B正确;
普通列车从乙地到达甲地时间是12小时,故选项C错误;
普通列出的速度为1000÷12=(千米/小时),动车的速度为:1000÷3﹣=250(千米/小时),故选项D正确;
故选:C.
13.解:由题意可得,
Q=50﹣5t,
当t=0时,Q=50,当Q=0时,t=10,
故选:C.
14.解:设y与x的函数关系为y=kx+b,由题意得:
,
解得:,
∴y=5000x+2000,
当x=0时,
y=5000×0+2000=2000,
∴营销人员没有销售量时最低收入是2000元,
故选:B.
15.解:由图可知,
乙晚出发1小时,故①正确;
乙出发3﹣1=2小时后追上甲,故②错误;
甲的速度是:18÷3=6(千米/小时),故③正确;
乙先到达B地,故④正确;
故选:B.
16.解:由图象得出小明步行720米,需要9分钟,
所以小明的运动速度为:720÷9=80(m/分),
当第15分钟时,小华运动15﹣9=6(分钟),
运动距离为:15×80=1200(m),
∴小华的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明小华已经到达终点,则小华先到达青少年宫,(故①正确);
此时小华运动19﹣9=10(分钟),
运动总距离为:10×200=2000(m),
∴小明运动时间为:2000÷80=25(分钟),
故a的值为25,(故③错误);
∵小明19分钟运动距离为:19×80=1520(m),
∴b=2000﹣1520=480,(故④正确).
故正确的有:①②④.
故选:A.
17.解:A、依题意他离家8km共用了30min,故选项正确;
B、依题意在第10min开始等公交车,第16min结束,故他等公交车时间为6min,故选项正确;
C、他步行10min走了1000m,故他步行的速度为他步行的速度是100m/min,故选项正确;
D、公交车(30﹣16)min走了(8﹣1)km,故公交车的速度为7000÷14=500m/min,故选项错误.
故选:D.
18.解:由图可得,
A、B两村相距8km,故①正确;
甲出发1.5h后到达C村,故②错误;
甲每小时比乙多骑行8km,故③正确;
相遇后,乙又骑行了=15min或(1.5﹣1)×60+=45min时两人相距2km,故④正确;
故选:C.
19.解:设甲乙两地的路程为s,从甲地到乙地的速度为v,从乙地到甲地的时间为t,
则
解得,t=1.8
∴a=3.2+1.8=5(小时),
故选:B.
20.解:①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(24﹣4)=60(m/min),
甲的速度为1200÷12﹣60=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②正确;
③b=(60+40)×(24﹣4﹣12)=800,结论③正确;
④a=1200÷40+4=34,结论④错误.
故结论正确的有①②③,
故选:B.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
