湘教版(2012)初中数学七年级下册 4.1相交直线所成的角 教案
文档属性
| 名称 | 湘教版(2012)初中数学七年级下册 4.1相交直线所成的角 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览


文档简介
教
案
NO
课
题
相交直线所成的角(2)
课
型
新授
教
学
目
标
知
识
与技能
1、使学生理解三线八角的意义
2、能从复杂图形中识别同位角、内错角、同旁内角。
过
程
与方法
通过动口
、动脑、动手、合作和探究,启发学生的智慧,感受快乐数学,
接受逻辑推理思维的熏陶。
情
感
态
度
价值观
通过三线八角的特点的分析,培养学生抽象概括问题的能力
使学生认识图形是由简到繁组合而成,培养学生形成基本图形的结构的能力
教
学
重
点
三线八角
教
学
难
点
三线八角
教
具
准
备
投影仪
教
学
过
程
教
师
活
动
学
生
活
动
一、创设情境,导入新课
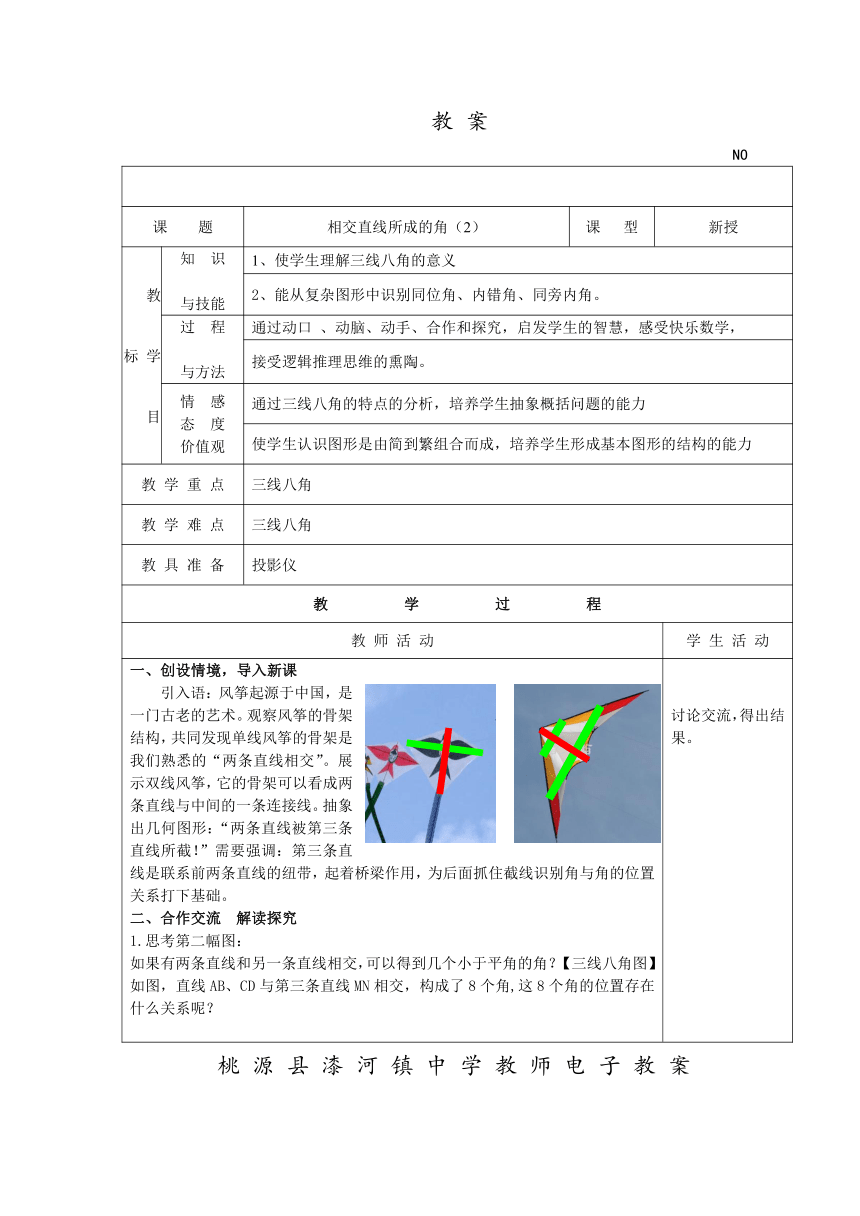
引入语:风筝起源于中国,是一门古老的艺术。观察风筝的骨架结构,共同发现单线风筝的骨架是我们熟悉的“两条直线相交”。展示双线风筝,它的骨架可以看成两条直线与中间的一条连接线。抽象出几何图形:“两条直线被第三条直线所截!”需要强调:第三条直线是联系前两条直线的纽带,起着桥梁作用,为后面抓住截线识别角与角的位置关系打下基础。
二、合作交流
解读探究
1.思考第二幅图:
如果有两条直线和另一条直线相交,可以得到几个小于平角的角?【三线八角图】
如图,直线AB、CD与第三条直线MN相交,构成了8个角,这8个角的位置存在什么关系呢?
讨论交流,得出结果。
桃
源
县
漆
河
镇
中
学
教
师
电
子
教
案
教
学
过
程
教
师
活
动
学
生
活
动
2.共同探索同位角的概念
问题探究:∠1与∠5具有什么样的位置关系?
①它们在被截直线a、b的位置?
②它们在截线c的位置?
③分离出来的1对同位角,从形状上观察,发现了什么?(字母F型)
3.小组合作探索内错角、同旁内角的位置特征
问题探索:类比上面的探索过程,小组合作完成∠1与∠6
、
∠1与∠7的位置关系(见附表1),班级交流规范说法后,再统一给出名称。
角位置关系名称∠1与∠5都在直线AB、CD的___,都在直线MN的____∠3与∠5都在在直线AB、CD的___,∠3在MN的___,∠5在MN的____∠3与∠6都在在直线AB、CD__,都在MN的___
附表一:角与角有哪些位置关系?——让我们一起来归纳
概念1:两条直线被第三条直线所截,在截线的同旁(侧),被截两直线的同一方,我们把这种位置关系的一对角称为同位角。
概念2:两条直线被第三条直线所截,有两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角
概念3:两条直线被第三条直线所截,在截线同旁,且在截线之内的一对角,叫做同旁内角。
④找出图中剩余的同位角、内错角、同旁内角。
三、应用迁移,巩固提高
例一.如图,直线EF与AB、CD相交,构成8个角。
指出图中所有的对顶角、同位角、内错角和同旁内角。
例二.如图,直线AB、CD被直线MN所截,同位角∠1与∠2
相等,那么内错角∠2与∠3相等吗?
师生共同讨论交流
学生积极发言
桃
源
县
漆
河
镇
中
学
教
师
电
子
教
案
教
学
过
程
教
师
活
动
学
生
活
动
【变式练习】
1、如右图,∠1、∠2是内错角,是(
)
A.AD、BC被AC所截构成的,
B.AB、DC被AC所截构成的
C.AB、BC被AC所截构成的,
D.AD、DC被AC所截构成的
【解析:分别做AB、CD两端延长线,即可清晰看出。】
答案:B
2、如右图,直线a、b被直线c所截,找出图中所有的同位角、内错角、同旁内角.
【解析:∠1和∠4、∠2和∠5是同位角,
∠3和∠4是内错角,∠2和∠4是同旁内角。】
四、动手操作、发现乐趣
1.看一看,右图文字中有对顶角、同位角、内错角、
同旁内角吗?
2.说一说,还有哪些字母中包含有这些角?
3.做一做,两只手的食子和拇指在同一平面内,它们
构成的一对角可以看成是什么角?类似地,你还能用两
只手的手指构成同位角和同旁内角吗?
4.游戏——旋转魔盘。“旋转魔盘”是一款flash小游戏,学生需要通过走上讲台操控计算机,参照给定转盘的位置将另一个转盘转到正确位置,从而创造出同位角、内错角、同旁内角。
五、课堂小结、共同归纳
六、拓展练习
A层:
1.如图所示,直线AB,CD相交于O,所形成的∠1,∠2,∠3,∠4中,下列四种分类不同于其他三个的是( )
A.∠1和∠2
B.∠2和∠3
C.∠3和∠4
D.∠2和∠4
2.下列说法错误的是( )
A.∠1和∠3是同位角
B.∠1和∠5是同位角
C.∠1和∠2是同旁内角
D.∠5和∠6是内错角
3.如图,其中内错角有( )
A.1对
B.2对
C.3对
D.4对
B层:
1、已知如图:
(1)∠1与∠2是 被 所截
成的 角;
(2)∠2与∠3是 被
截成的 角;
(3)∠3与∠A是 被 截成的 角;
(4)AB,AC被BE截成的同位角 ,内错角 ,同旁内角 ;
(5)DE,BC被AB截成的同位角是 ,内错角 ,同旁内角 .
完成练习
讨论交流
课堂小结
(1)在所学的知识中,直线的位置关系是怎样形成和发展的?
(2)学了哪些相互关系的角?
(3)寻找同位角、内错角和同旁内角关键应准确找到什么?
布置作业
练习1、2、3
板
书
设
计
相交直线所成的角
教
学
后
记
案
NO
课
题
相交直线所成的角(2)
课
型
新授
教
学
目
标
知
识
与技能
1、使学生理解三线八角的意义
2、能从复杂图形中识别同位角、内错角、同旁内角。
过
程
与方法
通过动口
、动脑、动手、合作和探究,启发学生的智慧,感受快乐数学,
接受逻辑推理思维的熏陶。
情
感
态
度
价值观
通过三线八角的特点的分析,培养学生抽象概括问题的能力
使学生认识图形是由简到繁组合而成,培养学生形成基本图形的结构的能力
教
学
重
点
三线八角
教
学
难
点
三线八角
教
具
准
备
投影仪
教
学
过
程
教
师
活
动
学
生
活
动
一、创设情境,导入新课
引入语:风筝起源于中国,是一门古老的艺术。观察风筝的骨架结构,共同发现单线风筝的骨架是我们熟悉的“两条直线相交”。展示双线风筝,它的骨架可以看成两条直线与中间的一条连接线。抽象出几何图形:“两条直线被第三条直线所截!”需要强调:第三条直线是联系前两条直线的纽带,起着桥梁作用,为后面抓住截线识别角与角的位置关系打下基础。
二、合作交流
解读探究
1.思考第二幅图:
如果有两条直线和另一条直线相交,可以得到几个小于平角的角?【三线八角图】
如图,直线AB、CD与第三条直线MN相交,构成了8个角,这8个角的位置存在什么关系呢?
讨论交流,得出结果。
桃
源
县
漆
河
镇
中
学
教
师
电
子
教
案
教
学
过
程
教
师
活
动
学
生
活
动
2.共同探索同位角的概念
问题探究:∠1与∠5具有什么样的位置关系?
①它们在被截直线a、b的位置?
②它们在截线c的位置?
③分离出来的1对同位角,从形状上观察,发现了什么?(字母F型)
3.小组合作探索内错角、同旁内角的位置特征
问题探索:类比上面的探索过程,小组合作完成∠1与∠6
、
∠1与∠7的位置关系(见附表1),班级交流规范说法后,再统一给出名称。
角位置关系名称∠1与∠5都在直线AB、CD的___,都在直线MN的____∠3与∠5都在在直线AB、CD的___,∠3在MN的___,∠5在MN的____∠3与∠6都在在直线AB、CD__,都在MN的___
附表一:角与角有哪些位置关系?——让我们一起来归纳
概念1:两条直线被第三条直线所截,在截线的同旁(侧),被截两直线的同一方,我们把这种位置关系的一对角称为同位角。
概念2:两条直线被第三条直线所截,有两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角
概念3:两条直线被第三条直线所截,在截线同旁,且在截线之内的一对角,叫做同旁内角。
④找出图中剩余的同位角、内错角、同旁内角。
三、应用迁移,巩固提高
例一.如图,直线EF与AB、CD相交,构成8个角。
指出图中所有的对顶角、同位角、内错角和同旁内角。
例二.如图,直线AB、CD被直线MN所截,同位角∠1与∠2
相等,那么内错角∠2与∠3相等吗?
师生共同讨论交流
学生积极发言
桃
源
县
漆
河
镇
中
学
教
师
电
子
教
案
教
学
过
程
教
师
活
动
学
生
活
动
【变式练习】
1、如右图,∠1、∠2是内错角,是(
)
A.AD、BC被AC所截构成的,
B.AB、DC被AC所截构成的
C.AB、BC被AC所截构成的,
D.AD、DC被AC所截构成的
【解析:分别做AB、CD两端延长线,即可清晰看出。】
答案:B
2、如右图,直线a、b被直线c所截,找出图中所有的同位角、内错角、同旁内角.
【解析:∠1和∠4、∠2和∠5是同位角,
∠3和∠4是内错角,∠2和∠4是同旁内角。】
四、动手操作、发现乐趣
1.看一看,右图文字中有对顶角、同位角、内错角、
同旁内角吗?
2.说一说,还有哪些字母中包含有这些角?
3.做一做,两只手的食子和拇指在同一平面内,它们
构成的一对角可以看成是什么角?类似地,你还能用两
只手的手指构成同位角和同旁内角吗?
4.游戏——旋转魔盘。“旋转魔盘”是一款flash小游戏,学生需要通过走上讲台操控计算机,参照给定转盘的位置将另一个转盘转到正确位置,从而创造出同位角、内错角、同旁内角。
五、课堂小结、共同归纳
六、拓展练习
A层:
1.如图所示,直线AB,CD相交于O,所形成的∠1,∠2,∠3,∠4中,下列四种分类不同于其他三个的是( )
A.∠1和∠2
B.∠2和∠3
C.∠3和∠4
D.∠2和∠4
2.下列说法错误的是( )
A.∠1和∠3是同位角
B.∠1和∠5是同位角
C.∠1和∠2是同旁内角
D.∠5和∠6是内错角
3.如图,其中内错角有( )
A.1对
B.2对
C.3对
D.4对
B层:
1、已知如图:
(1)∠1与∠2是 被 所截
成的 角;
(2)∠2与∠3是 被
截成的 角;
(3)∠3与∠A是 被 截成的 角;
(4)AB,AC被BE截成的同位角 ,内错角 ,同旁内角 ;
(5)DE,BC被AB截成的同位角是 ,内错角 ,同旁内角 .
完成练习
讨论交流
课堂小结
(1)在所学的知识中,直线的位置关系是怎样形成和发展的?
(2)学了哪些相互关系的角?
(3)寻找同位角、内错角和同旁内角关键应准确找到什么?
布置作业
练习1、2、3
板
书
设
计
相交直线所成的角
教
学
后
记
