4.2 直线、射线、线段 第2课时 线段的比较与运算 课件(共27张PPT)
文档属性
| 名称 | 4.2 直线、射线、线段 第2课时 线段的比较与运算 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 23:09:18 | ||
图片预览








文档简介
(共27张PPT)
人教版
七上
第四章
几何图形初步
4.2
直线、射线、线段
第2课时
线段的比较与运算
教学重点:
尺规画一条线段等于已知线段及比较两条线段的长短.
教学难点:
线段的和、差、倍、分关系及线段中点的运用.
情境引入
小红与小丽想比较一下身高,有什么方法比较小红与小丽的身高?
1.他们站在同一水平高度进行比较.
2.用卷尺测量他们的高度,再比较.
还有其它方法比较吗?
其实两名同学可以近似被看成是两条线段,那你们能否借助于比较两位同学身高的方法来比较两条线段的长短呢?
探究新知
思考:画一条线段等于已线段a.
a
度量法画法:
A
B
探究新知
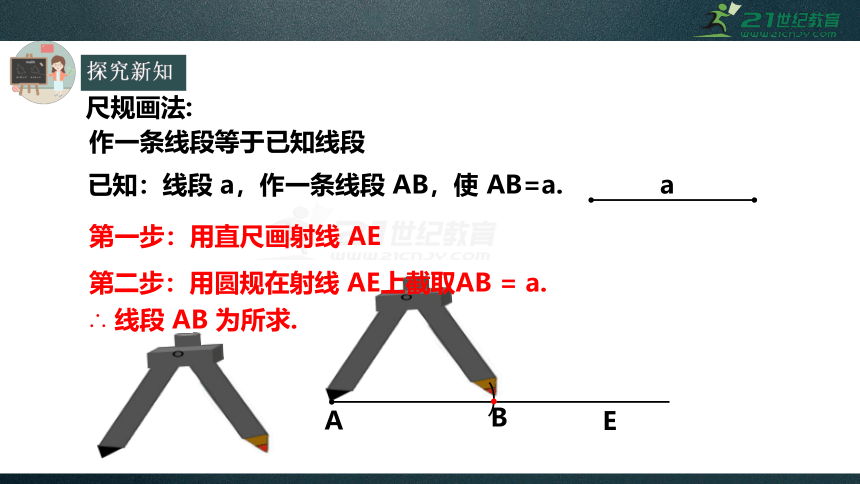
作一条线段等于已知线段
已知:线段
a,作一条线段
AB,使
AB=a.
尺规画法:
a
B
A
E
第一步:用直尺画射线
AE
第二步:用圆规在射线
AE上截取AB
=
a.
∴
线段
AB
为所求.
●
归纳
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
尺规作图:
探究新知
比较两条线段的长短方法
C
D
A
B
试比较线段AB,CD的长短.
1.度量法:
AB=2.5cm
CD=3.3cm
∴AB度量法:用刻度尺测量他们的长度,进行比较.(从“数”的角度去比较线段的长短)
探究新知
C
D
A
B
试比较线段AB,CD的长短.
1.将线段AB沿着线段CD的方向落下,线段AB的端点A与线段CD的端点C重合.
A
B
2.若端点B点落在端点C,D之间,则得到线段AB小于线段CD.
∴AB探究新知
C
D
A
B
试比较线段AB,CD的长短.
1.将线段AB沿着线段CD的方向落下,线段AB的端点A与线段CD的端点C重合.
2.若端点B与端点D重合,则得到线段AB等于线段CD.
∴AB=CD
A
B
探究新知
C
D
A
B
试比较线段AB,CD的长短.
1.将线段AB沿着线段CD的方向落下,线段AB的端点A与线段CD的端点C重合.
2.若端点B落在CD的延长线上,则得到线段AB大于线段CD.
∴AB>CD
A
B
归纳
先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置来比较长短.
简单记为:起点对齐,看终点.
叠合法:
练一练
1.尺规作图的工具是(
).
A
刻度尺和圆规
B
三角板和量角器
C
直尺和量角器
D
没有刻度的直尺和圆规
2.为了比较线段AB,CD的大小,小明将点A与点C重合使两条线段在一条直线上,结果点B在CD的延长线上,则(
).
A
AB>CD
B
ABC
AB=CD
D
无法确定
D
A
探究新知
如图,已知线段a、b画一条线段,使它等于a+b.
解:(1)作射线OP;
(2)在射线OP上依次截取OA=a,AB=a;
OB就是所求的线段.
b
a
A
●
B
●
O
P
即:OB=OA+AB=a+b
探究新知
如图,已知线段a、b画一条线段,使它等于2a-b.
解:(1)作射线OP;
(2)在射线OP上依次截取OA=a,AB=a;
(3)在线段OB上截取BC=b,则OC=2a-b,
OC就是所求的线段.
b
a
A
●
B
●
C
●
O
P
归纳
A
B
C
②线段AB、AC的差等于线段BC.
①线段AC、BC的和等于线段AB.
符号语言:AC+BC=AB.
符号语言:AB-AC=BC.
③线段AB、BC的差等于线段AC.
符号语言:AB-BC=AC.
如图所示,图中共有三条不同的线段,它们和差关系如下:
练一练
1.如图1,AB=CD,填空:
2.如图,已知线段a、b画一条线段,使它等于a-b.
●
●
A
B
D
C
图1
a
b
AD=
+
+CD=
+CD
=
+BD
AC=
-CD;
BC=
-AB;
(3)BD=
+CD;
AB
BC
AC
AB
AD
AC
BC
∴AC=
=
AB
探究新知
如图,把一条线段分成
的两条线段的点叫做这条线段的中点.
●
B
A
C
相等
中点
BC
∵C是AB的中点
几何语言:
或AB
=
AC=
BC
.
2
2
反之也成立:
∵
AC=BC=
AB
或AB
=2AC=2BC
.
∴
C是AB的中点.
∴AC=
=
=
AB
探究新知
如何表示三等分点?四等分点呢?
CD
∵C,D是线段AB的三等分点.
几何语言:
●
B
A
C
●
D
如图,C,D是线段AB的三等分点.
BD
N
M
E
F
G
●
●
●
如图E,F,G是线段MN的四等分点.
几何语言:
∵
E,F,G是线段MN的四等分点.
∴ME=
=
=
=
AB
EF
FG
GN
例题讲解
例
如图,已知B,C两点把线段
AD
分成
2∶3∶4的三部分,点E是线段AD的中点,且EC=2cm.求AD,BE的长.
分析:已知B,C两点把线段AD分成
2∶3∶4
的三部分,也就是如果把线段AD分成相等的9份,那么AB占有
2
份,BC占有
3
份,CD占有4
份,因此可设每一份为xcm,则AB=2xcm,BC=3xcm,CD=4xcm.
例题讲解
解:设每一份为xcm,则AB=2xcm,BC=3xcm,CD=4xcm,根据题意,得
AD=AB+BC+CD=9x
E是线段AD的中点
EC=ED-CD=4.5x-4x=0.5X
即0.5x=2
解得x=4
ED=
AD=4.5x
所以AB=8cm,BC=12cm,CD=16cm
例题讲解
所以AD=AB+
BC
+
CD
=8+12+16=36cm
AE=
AD=18
cm
BE=AE-AB=18-8=10cm
课堂练习
1.根据图中填空:
(1)
AD-
=AC
;
AB+
=AC
(2)
BD-BC=
-AC
;
AB+BC=AD-
.
2.如图,点C是线段AD的中点,点B是线段AC的中点,如果BC=3cm,则AD的长为(
)
A.3
cm
B.6
cm
C.9
cm
D.12
cm
CD
BC
AD
CD
D
课堂练习
3.如果点M在线段AB上,下列表达式中不能表示点M是线段AC中点的有(
).
B
A
AM=MB
B
AM=AB
C
AB=2AM
D
AM=
AB
课堂练习
4.如图,点D为线段AB的中点,点C为线段AD的中点,若AB=8cm,求线段BC的长度.
解:因为AB=8cm,D是AB的中点
所以AD=
AB
=4cm;
因为C是AD的中点,
所以AC=
AD=2cm
●
●
●
●
B
A
D
C
BC=AB-AC=6cm
课堂小结
1.
画一条线段等于已知线段.
2.
比较两条线段的大小的两种方法.
3.
中点的定义及有关中点运算.
课外作业
第123页第1、2、3题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
第四章
几何图形初步
4.2
直线、射线、线段
第2课时
线段的比较与运算
教学重点:
尺规画一条线段等于已知线段及比较两条线段的长短.
教学难点:
线段的和、差、倍、分关系及线段中点的运用.
情境引入
小红与小丽想比较一下身高,有什么方法比较小红与小丽的身高?
1.他们站在同一水平高度进行比较.
2.用卷尺测量他们的高度,再比较.
还有其它方法比较吗?
其实两名同学可以近似被看成是两条线段,那你们能否借助于比较两位同学身高的方法来比较两条线段的长短呢?
探究新知
思考:画一条线段等于已线段a.
a
度量法画法:
A
B
探究新知
作一条线段等于已知线段
已知:线段
a,作一条线段
AB,使
AB=a.
尺规画法:
a
B
A
E
第一步:用直尺画射线
AE
第二步:用圆规在射线
AE上截取AB
=
a.
∴
线段
AB
为所求.
●
归纳
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
尺规作图:
探究新知
比较两条线段的长短方法
C
D
A
B
试比较线段AB,CD的长短.
1.度量法:
AB=2.5cm
CD=3.3cm
∴AB
探究新知
C
D
A
B
试比较线段AB,CD的长短.
1.将线段AB沿着线段CD的方向落下,线段AB的端点A与线段CD的端点C重合.
A
B
2.若端点B点落在端点C,D之间,则得到线段AB小于线段CD.
∴AB
C
D
A
B
试比较线段AB,CD的长短.
1.将线段AB沿着线段CD的方向落下,线段AB的端点A与线段CD的端点C重合.
2.若端点B与端点D重合,则得到线段AB等于线段CD.
∴AB=CD
A
B
探究新知
C
D
A
B
试比较线段AB,CD的长短.
1.将线段AB沿着线段CD的方向落下,线段AB的端点A与线段CD的端点C重合.
2.若端点B落在CD的延长线上,则得到线段AB大于线段CD.
∴AB>CD
A
B
归纳
先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置来比较长短.
简单记为:起点对齐,看终点.
叠合法:
练一练
1.尺规作图的工具是(
).
A
刻度尺和圆规
B
三角板和量角器
C
直尺和量角器
D
没有刻度的直尺和圆规
2.为了比较线段AB,CD的大小,小明将点A与点C重合使两条线段在一条直线上,结果点B在CD的延长线上,则(
).
A
AB>CD
B
AB
AB=CD
D
无法确定
D
A
探究新知
如图,已知线段a、b画一条线段,使它等于a+b.
解:(1)作射线OP;
(2)在射线OP上依次截取OA=a,AB=a;
OB就是所求的线段.
b
a
A
●
B
●
O
P
即:OB=OA+AB=a+b
探究新知
如图,已知线段a、b画一条线段,使它等于2a-b.
解:(1)作射线OP;
(2)在射线OP上依次截取OA=a,AB=a;
(3)在线段OB上截取BC=b,则OC=2a-b,
OC就是所求的线段.
b
a
A
●
B
●
C
●
O
P
归纳
A
B
C
②线段AB、AC的差等于线段BC.
①线段AC、BC的和等于线段AB.
符号语言:AC+BC=AB.
符号语言:AB-AC=BC.
③线段AB、BC的差等于线段AC.
符号语言:AB-BC=AC.
如图所示,图中共有三条不同的线段,它们和差关系如下:
练一练
1.如图1,AB=CD,填空:
2.如图,已知线段a、b画一条线段,使它等于a-b.
●
●
A
B
D
C
图1
a
b
AD=
+
+CD=
+CD
=
+BD
AC=
-CD;
BC=
-AB;
(3)BD=
+CD;
AB
BC
AC
AB
AD
AC
BC
∴AC=
=
AB
探究新知
如图,把一条线段分成
的两条线段的点叫做这条线段的中点.
●
B
A
C
相等
中点
BC
∵C是AB的中点
几何语言:
或AB
=
AC=
BC
.
2
2
反之也成立:
∵
AC=BC=
AB
或AB
=2AC=2BC
.
∴
C是AB的中点.
∴AC=
=
=
AB
探究新知
如何表示三等分点?四等分点呢?
CD
∵C,D是线段AB的三等分点.
几何语言:
●
B
A
C
●
D
如图,C,D是线段AB的三等分点.
BD
N
M
E
F
G
●
●
●
如图E,F,G是线段MN的四等分点.
几何语言:
∵
E,F,G是线段MN的四等分点.
∴ME=
=
=
=
AB
EF
FG
GN
例题讲解
例
如图,已知B,C两点把线段
AD
分成
2∶3∶4的三部分,点E是线段AD的中点,且EC=2cm.求AD,BE的长.
分析:已知B,C两点把线段AD分成
2∶3∶4
的三部分,也就是如果把线段AD分成相等的9份,那么AB占有
2
份,BC占有
3
份,CD占有4
份,因此可设每一份为xcm,则AB=2xcm,BC=3xcm,CD=4xcm.
例题讲解
解:设每一份为xcm,则AB=2xcm,BC=3xcm,CD=4xcm,根据题意,得
AD=AB+BC+CD=9x
E是线段AD的中点
EC=ED-CD=4.5x-4x=0.5X
即0.5x=2
解得x=4
ED=
AD=4.5x
所以AB=8cm,BC=12cm,CD=16cm
例题讲解
所以AD=AB+
BC
+
CD
=8+12+16=36cm
AE=
AD=18
cm
BE=AE-AB=18-8=10cm
课堂练习
1.根据图中填空:
(1)
AD-
=AC
;
AB+
=AC
(2)
BD-BC=
-AC
;
AB+BC=AD-
.
2.如图,点C是线段AD的中点,点B是线段AC的中点,如果BC=3cm,则AD的长为(
)
A.3
cm
B.6
cm
C.9
cm
D.12
cm
CD
BC
AD
CD
D
课堂练习
3.如果点M在线段AB上,下列表达式中不能表示点M是线段AC中点的有(
).
B
A
AM=MB
B
AM=AB
C
AB=2AM
D
AM=
AB
课堂练习
4.如图,点D为线段AB的中点,点C为线段AD的中点,若AB=8cm,求线段BC的长度.
解:因为AB=8cm,D是AB的中点
所以AD=
AB
=4cm;
因为C是AD的中点,
所以AC=
AD=2cm
●
●
●
●
B
A
D
C
BC=AB-AC=6cm
课堂小结
1.
画一条线段等于已知线段.
2.
比较两条线段的大小的两种方法.
3.
中点的定义及有关中点运算.
课外作业
第123页第1、2、3题
https://www.21cnjy.com/help/help_extract.php
