人教版八年级上册 第十二章 全等三角形:构造全等三角形的方法(例题+练习 无答案)
文档属性
| 名称 | 人教版八年级上册 第十二章 全等三角形:构造全等三角形的方法(例题+练习 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 192.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
【构造全等三角形的方法】
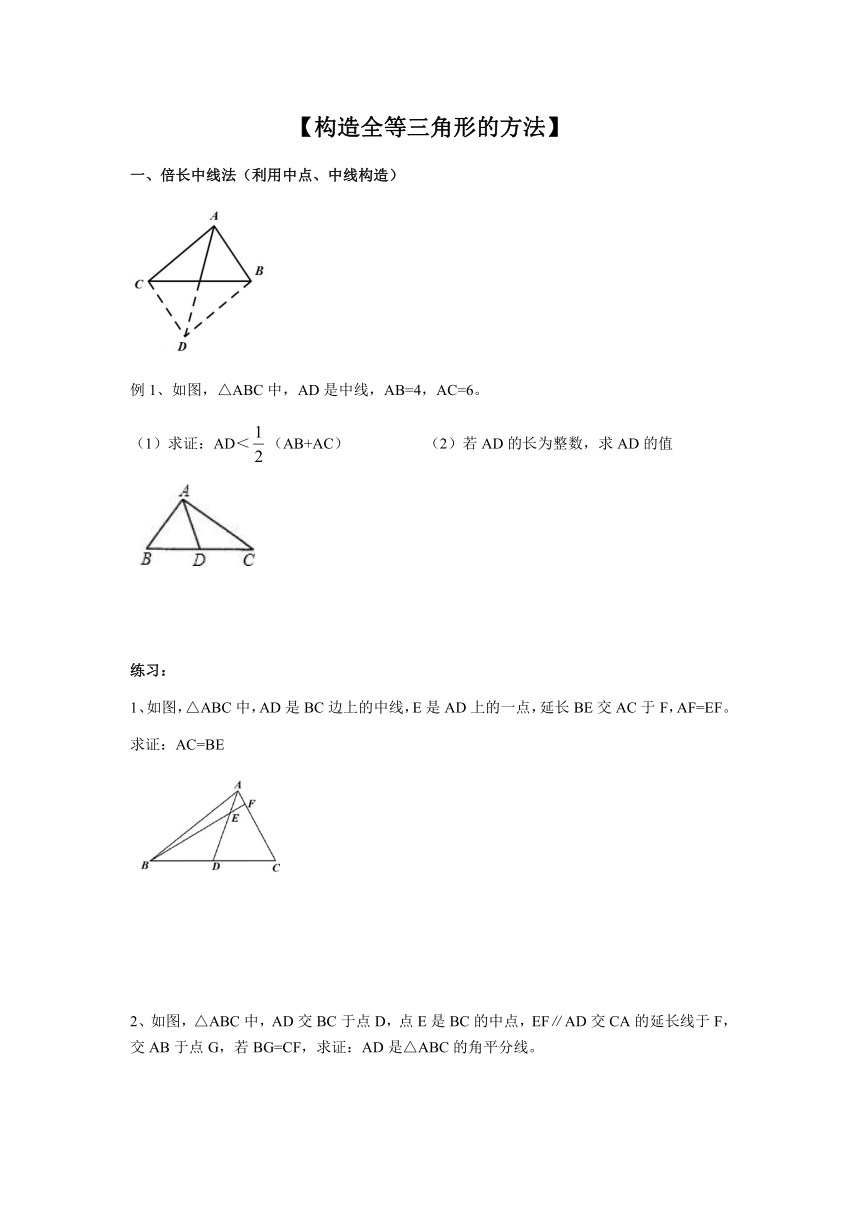
倍长中线法(利用中点、中线构造)
如图,△ABC中,AD是中线,AB=4,AC=6。
(1)求证:AD<(AB+AC)
(2)若AD的长为整数,求AD的值
练习:
1、如图,△ABC中,AD是BC边上的中线,E是AD上的一点,延长BE交AC于F,AF=EF。
求证:AC=BE
2、如图,△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于F,交AB于点G,若BG=CF,求证:AD是△ABC的角平分线。
利用角平分线
例1、已知:∠1=∠2,∠3=∠4。求证:AP平分∠BAC
例2、BE是角平分线,AD垂直BE于D,求证:∠2=∠1+∠C
例3、已知在△
ABC中,∠B=2∠C,∠A的平分线AD交BC边于点D.求证:AC=AB+BD.
练习:
如图,已知∠1=∠2,P是BN上的一点,PF⊥BC于F,PA=PC.
求证:∠PCB+∠BAP=180°
如图,已知∠BAC=90°,AB=AC,BD是∠ABC的角平分线,且CE⊥BD交BD的延长线于点E。
求证:BD=2CE
三、截长补短法(通常用来证明线段和差相等)
例1、如图(1)已知:正方形ABCD中,∠BAC的平分线交BC于E,
求证:AB+BE=AC.
例2、AB//CD,BE,CE是角平分线,求证:BC=AB+CD
练习:
1、如图所示,已知△ABC中AB>AC,AD是∠BAC的平分线,M是AD上任意一点。
求证:MB
-
MC<AB
-
AC
2、如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明。
四、旋转法
对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形
例1、如图,正方形ABCD中,DE=3,BF=1,∠EAF=45°,求证:EF=BF+DE.
练习:如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为
五、平行线法(平移法)
例1、如图,△ABC中,AB=AC。E是AB上异于A、B的任意一点,延长AC到D,使CD=BE,连接DE交BC于F。求证:EF=FD。
作业:
1、如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.
如图,E、F分别是正方形ABCD的边BC、CD上的点,且∠EAF=45°,AH⊥EF,H为垂足。
求证:(1)BE+DF=EF
(2)AH=AB
3、如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的角平分线,AD、CE相交于点F。请判断FE与FD之间的数量关系。
倍长中线法(利用中点、中线构造)
如图,△ABC中,AD是中线,AB=4,AC=6。
(1)求证:AD<(AB+AC)
(2)若AD的长为整数,求AD的值
练习:
1、如图,△ABC中,AD是BC边上的中线,E是AD上的一点,延长BE交AC于F,AF=EF。
求证:AC=BE
2、如图,△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于F,交AB于点G,若BG=CF,求证:AD是△ABC的角平分线。
利用角平分线
例1、已知:∠1=∠2,∠3=∠4。求证:AP平分∠BAC
例2、BE是角平分线,AD垂直BE于D,求证:∠2=∠1+∠C
例3、已知在△
ABC中,∠B=2∠C,∠A的平分线AD交BC边于点D.求证:AC=AB+BD.
练习:
如图,已知∠1=∠2,P是BN上的一点,PF⊥BC于F,PA=PC.
求证:∠PCB+∠BAP=180°
如图,已知∠BAC=90°,AB=AC,BD是∠ABC的角平分线,且CE⊥BD交BD的延长线于点E。
求证:BD=2CE
三、截长补短法(通常用来证明线段和差相等)
例1、如图(1)已知:正方形ABCD中,∠BAC的平分线交BC于E,
求证:AB+BE=AC.
例2、AB//CD,BE,CE是角平分线,求证:BC=AB+CD
练习:
1、如图所示,已知△ABC中AB>AC,AD是∠BAC的平分线,M是AD上任意一点。
求证:MB
-
MC<AB
-
AC
2、如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明。
四、旋转法
对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形
例1、如图,正方形ABCD中,DE=3,BF=1,∠EAF=45°,求证:EF=BF+DE.
练习:如图所示,两个边长都为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕O点旋转,那么它们重叠部分的面积为
五、平行线法(平移法)
例1、如图,△ABC中,AB=AC。E是AB上异于A、B的任意一点,延长AC到D,使CD=BE,连接DE交BC于F。求证:EF=FD。
作业:
1、如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.
如图,E、F分别是正方形ABCD的边BC、CD上的点,且∠EAF=45°,AH⊥EF,H为垂足。
求证:(1)BE+DF=EF
(2)AH=AB
3、如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的角平分线,AD、CE相交于点F。请判断FE与FD之间的数量关系。
