苏科版八年级数学上册 第六章 一次函数 单元检测试题(Word版有答案)
文档属性
| 名称 | 苏科版八年级数学上册 第六章 一次函数 单元检测试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 11:34:46 | ||
图片预览



文档简介
第六章
一次函数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
在圆的面积计算公式中,变量是(
)
A.
B.
C.,
D.,
?
2.
下列关系式中,不是的函数的是(
)
A.
B.
C.
D.
?
3.
如图,已知直线,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;…;按此作法继续下去,则点的坐标为(
)
A.
B.
C.
D.
?
4.
的底边上的高为,当它的底边从变化到时,的面积(????????)
A.从变化到
B.从变化到
C.从变化到
D.从变化到
?5.
笔记本每本元,买本笔记本共支出元,在这个问题中:
①是常量时,是变量;②是变量时,是常量;③是变量时,也是变量;
④,可以都是常量或都是变量.上述判断正确的有(
)
A.个
B.个
C.个
D.个
?
6.
以下是关于常量和变量的说法:
在一个变化过程中,允许出现多个变量和常量;
变量就是变量,它不可以转化为常量;
变量和常量是相对而言的,在一定条件下可以相互转化;
在一个变化过程中,变量只有个,常量可以没有,也可能有多个.
其中正确的说法有(
)
A.个
B.个
C.个
D.个
?
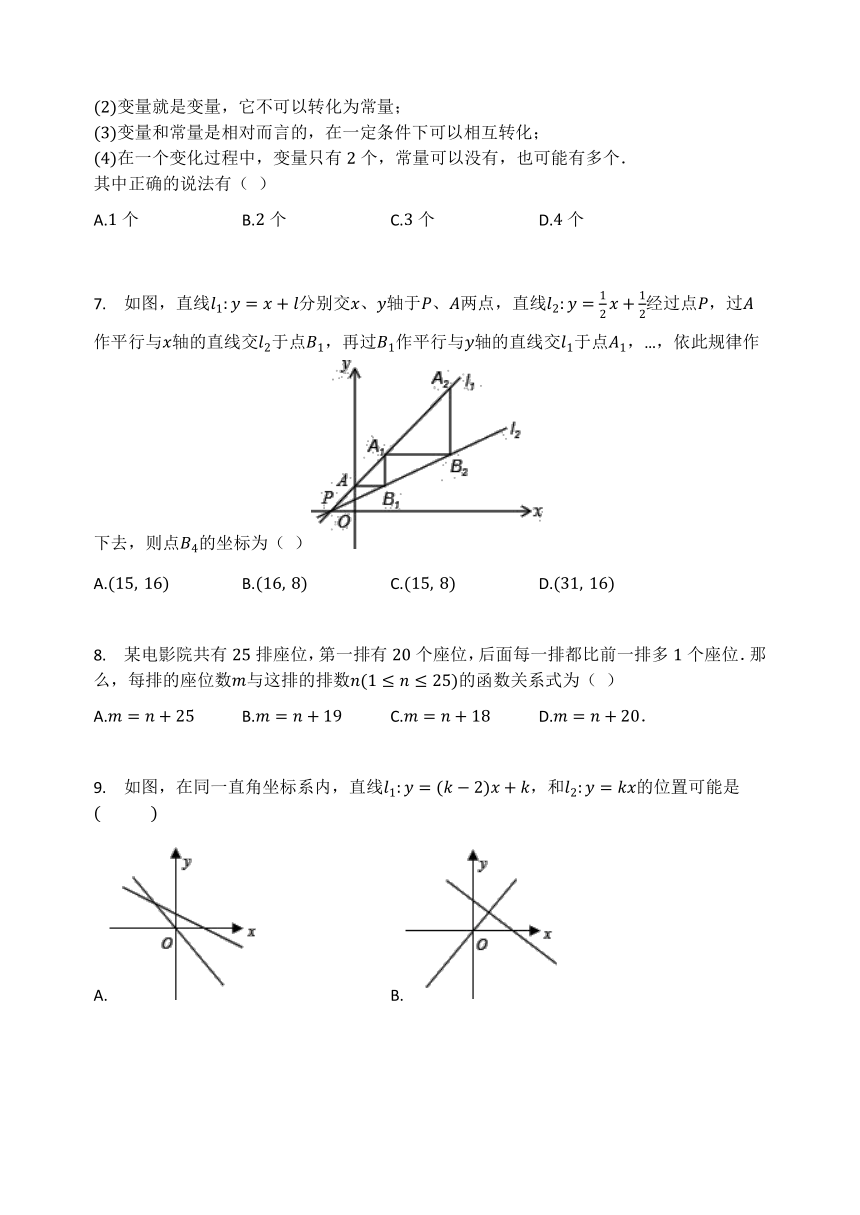
7.
如图,直线分别交、轴于、两点,直线经过点,过作平行与轴的直线交于点,再过作平行与轴的直线交于点,…,依此规律作下去,则点的坐标为(
)
A.
B.
C.
D.
?
8.
某电影院共有排座位,第一排有个座位,后面每一排都比前一排多个座位.那么,每排的座位数与这排的排数的函数关系式为(
)
A.
B.
C.
D..
?
9.
如图,在同一直角坐标系内,直线,和的位置可能是?
?
?
?
A.
B.
C.
D.
?
10.
弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的重量间有下面的关系:
下列说法不正确的是(
)
A.与都是变量,且是自变量,是因变量
B.物体质量每增加,弹簧长度增加
C.与的关系表达式是
D.所挂物体质量为时,弹簧长度为
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
函数的自变量的取值范围是________.
?
12.
若函数是一次函数,则________.
?
13.
已知函数,那么=________.
?
14.
已知是正比例函数,则的值是________.
?
15.
若关于的函数是一次函数,则________,________.
?
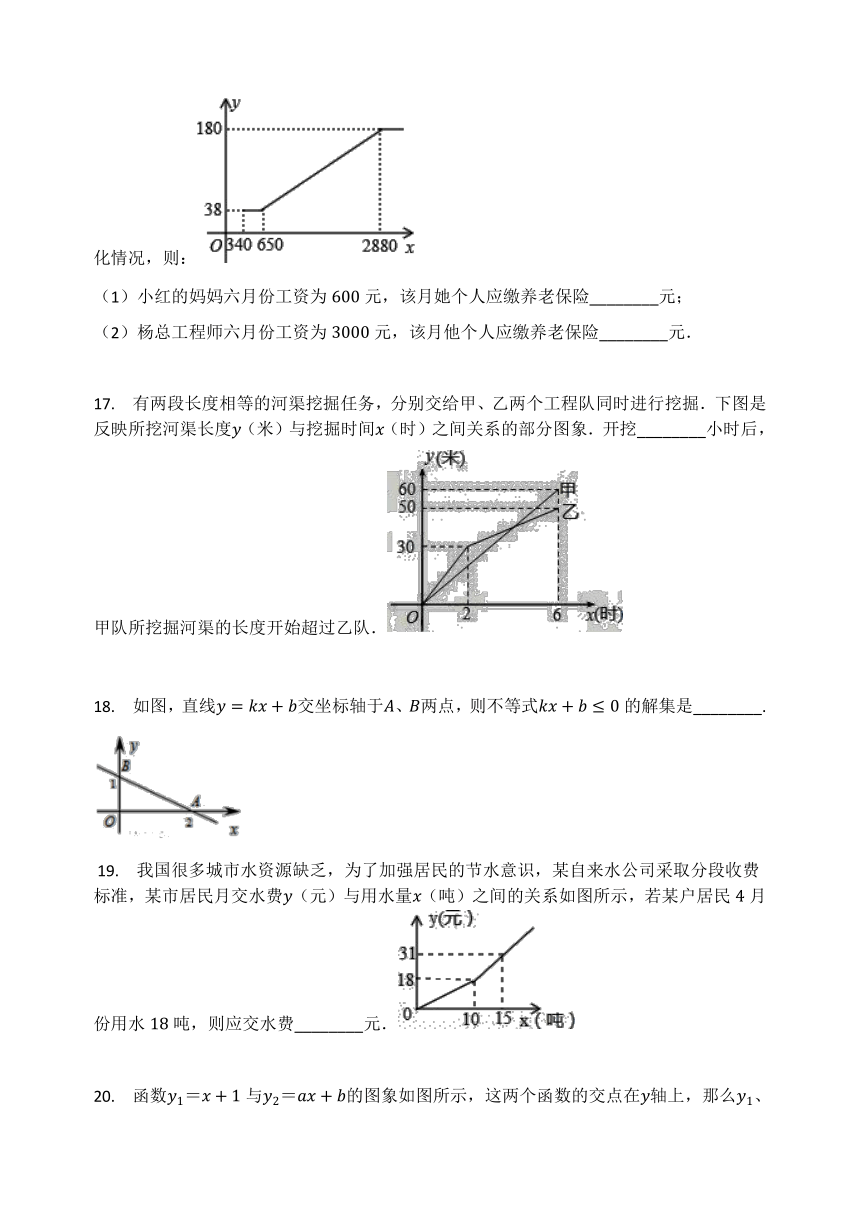
16.
如图所示,某市自来水公司职工养老保险个人月缴费(元)随个人工资(元)的变化情况,则:
(1)小红的妈妈六月份工资为元,该月她个人应缴养老保险________元;
(2)杨总工程师六月份工资为元,该月他个人应缴养老保险________元.
?
17.
有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.下图是反映所挖河渠长度(米)与挖掘时间(时)之间关系的部分图象.开挖________小时后,甲队所挖掘河渠的长度开始超过乙队.
?
18.
如图,直线交坐标轴于、两点,则不等式的解集是________.
?19.
我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费(元)与用水量(吨)之间的关系如图所示,若某户居民月份用水吨,则应交水费________元.
?
20.
函数=与=的图象如图所示,这两个函数的交点在轴上,那么、的值都大于零的的取值范围是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
在同一直角坐标系中画出下列一次函数的图象
(1)
(2)
(3)
(4).
?
22.
一列火车以的速度匀速行驶.
写出它行驶的路程与时间之间的函数表达式;
当时,是多少?
?
23.
一辆汽车油箱内有油升,从某地出发,每行驶小时耗油升,若设剩余油量为升,行驶时间为小时,根据以上信息回答下列问题:
(1)开始时,汽车的油量=________升;
(2)在________小时汽车加油,加了________升,写出加油前与之间的关系式________;
(3)这辆汽车行驶小时,剩余油量多少升?
?
24.
为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过时,水费按每立方米元收费,超过时,超过部分每立方米按元收费,设每户每月用水量为,应缴水费为元.
写出与之间的函数表达式;
如果有两户家庭某月份需缴纳水费为元和元时,求这两户家庭这个月的用水量分别是多少?
?
25.
有一科技小组进行了机器人行走性能试验.在试验场地有、、三点顺次在同一笔直的赛道上,甲、乙两机器人分别从、两点同时同向出发,历时
同时到达点,甲机器人前分钟以的速度行走,乙机器人始终以
的速度行走,如图是甲、乙两机器人之间的距离与他们的行走时间之间的函数图象,请结合图象,回答下列问题:
(1)、两点之间的距离是
,、两点之间的距离是
,=
.
(2)求线段所在直线的函数表达式.
(3)设线段轴,直接写出两机器人出发多长时间相距.
?
26.
某工厂有两批数量相同的产品生产任务,分别交给甲、乙两个小组同时进行生产.如图是反映生产数量(件)与生产时间之间关系的部分图象.请解答下列问题:
某工厂有两批数量相同的产品生产任务,分别交给甲、乙两个小组同时进行生产.如图是反映生产数量(件)与生产时间之间关系的部分图象.请解答下列问题:
乙小组生产到?件时,用了________.生产时,甲小组比乙小组多生产了________件;
请你求出:
①甲小组在的时段内,与之间的函数关系式;(直接写出结论)
②乙小组在的时段内,与之间的函数关系式;(直接写出结论)
③生产几小时后,甲小组所生产的数量开始超过乙小组?(要求写出过程)
如果甲小组生产速度不变,乙小组在生产后,生产速度增加到?件,结果两小组同时完成了任务.问甲小组从开始生产到完工所生产的数量为多少件?(要求写出过程)
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
解:在圆的面积计算公式中,变量为,.
故选.
2.
【答案】
C
【解答】
解:在图象,,中,每给一个值,都有个值与它对应,所以,,中是的函数,
在中,给一个正值,有个值与之对应,所以不是的函数.
故选:.
3.
【答案】
C
【解答】
解:∵
点的坐标是,
∴
,
∵
点在直线上,
∴
,
∴
,
∴
,
得出,
∴
,
∴
的坐标是.
故选.
4.
【答案】
B
【解答】
略
5.
【答案】
B
【解答】
解:由题意得:,
此问题中、都是变量,是常量,或,都是常量,则③④,
故选:.
6.
【答案】
B
【解答】
解:在一个变化过程中,允许出现多个变量和常量,对;
错,变量在一定的条件下可以互相转化常量,如中,一定,、就是变量,一定,、就是变量;
变量和常量往往是相对的,在一定的条件下可以互相转化,正确;
错误,在一个变化过程中,变量只有两个,常量不能没有,也可以是多个.
正确的有个,故选:.
7.
【答案】
C
【解答】
解:∵
直线交轴于点,
∴
当时,,即点坐标为,
∵
轴,
∴
点的纵坐标为,设,
∴
,解得;
∴
点的坐标为,即;
∵
轴,
∴
点的横坐标为,设,
∴
,
∴
点的坐标为;
同理,可得,即;
;
,即;
;
,即.
故选.
8.
【答案】
B
【解答】
解:第一排有个座位,
第二排有个座位,
第三排有个座位,
…,
第排有个座位.
故选.
9.
【答案】
B
【解答】
解:由题意知,分三种情况:
、当时,的图象经过第一、二、三象限;的图象随的增大而增大,并且比倾斜程度大,故选项错误;
、当时,的图象经过第一、二、四象限;的图象随的增大而增大,选项正确;
、当时,的图象经过第二、三、四象限,的图象随的增大而减小,但比倾斜程度大,故,选项错误.
故选.
10.
【答案】
C
【解答】
解:、随的增加而增加,是自变量,是因变量,故选项正确;
、物体质量每增加,弹簧长度增加,故选项正确;
、与的关系表达式是,故选项错误;
、由知,则当时,,即所挂物体质量为时,
弹簧长度为,故选项正确;
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:根据题意得:,
解得:.
故答案为:.
12.
【答案】
【解答】
解:∵
函数是一次函数,
∴
,,
∴
.
故答案为:.
13.
【答案】
【解答】
.
14.
【答案】
【解答】
解:∵
是正比例函数,
∴
且,
解得(不合题意,舍去)或
故答案是:.
15.
【答案】
,
【解答】
解:一次函数的定义条件是:、为常数,,自变量次数为,
∴
根据题意,知
,
解得,,
故答案是、.
16.
【答案】
;
(2)轴上所对应的函数图象上的的值为,故答案为.
【解答】
解:(1)轴上所对应的函数图象上的的值为,
(2)轴上所对应的函数图象上的的值为,
17.
【答案】
【解答】
解:因为甲超过乙在小时后,甲的速度一直是:米/时,乙两小时后的速度为:米/时,
设小时时,甲乙所挖的距离相等,
则,
解得.
18.
【答案】
【解答】
解:由图象可以看出,轴下方的函数图象所对应自变量的取值为,
故不等式的解集是.
故答案为:.
19.
【答案】
【解答】
解:将代入得:
,
解得:,
故
将,代入得:
,
解得:,
故解析式为:
把代入,
故答案为:
20.
【答案】
【解答】
根据图示及数据可知,
函数=与轴的交点坐标是,
由图可知=与轴的交点坐标是,
所以、的值都大于零的的取值范围是:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:如图:(1)图象过和;
(2)图象过和;
(3)图象过和;
(4)图象过和.
【解答】
解:如图:(1)图象过和;
(2)图象过和;
(3)图象过和;
(4)图象过和.
22.
【答案】
解:根据题意可得.
当时,
.
【解答】
解:根据题意可得.
当时,
.
23.
【答案】
,,=
这辆汽车行驶小时,剩余油量升
【解答】
开始时,汽车的油量=升;
故答案为:.
在小时汽车加油,加了:=(升),
机动车每小时的耗油量为=(升),
∴
加油前油箱剩余油量与行驶时间的函数关系为=.
故答案为:;;=.
=(升),
答:这辆汽车行驶小时,剩余油量升.
24.
【答案】
解:当时,;
当时,,
即,
所以与之间的函数表达式为
因为,
所以用水量不超过立方米,
所以当时,,解得.
因为,
所以用水量超过立方米,
所以当.时,,解得.
答:这两户家庭这个月的用水量分别为和.
【解答】
解:当时,;
当时,,
即,
所以与之间的函数表达式为
因为,
所以用水量不超过立方米,
所以当时,,解得.
因为,
所以用水量超过立方米,
所以当.时,,解得.
答:这两户家庭这个月的用水量分别为和.
25.
【答案】
由图象可知,、两点之间的距离是米,
甲机器人前分钟的速度为:=(米/分);
即=;
、两点之间的距离是:=.
故答案为:;;;
设线段所在直线的函数解析式为:=,
∵
=,
∴
点的坐标为,
则,
解得,
则线段所在直线的函数解析式为=;
如图,设,.
∵
,,
∴
线段所在直线的函数解析式为=,
∵
,,
∴
线段所在直线的函数解析式为,
设两机器人出发时相距,
由题意,可得=,或=,或,
解得=,或=,或=.
即两机器人出发或或时相距.
【解答】
由图象可知,、两点之间的距离是米,
甲机器人前分钟的速度为:=(米/分);
即=;
、两点之间的距离是:=.
故答案为:;;;
设线段所在直线的函数解析式为:=,
∵
=,
∴
点的坐标为,
则,
解得,
则线段所在直线的函数解析式为=;
如图,设,.
∵
,,
∴
线段所在直线的函数解析式为=,
∵
,,
∴
线段所在直线的函数解析式为,
设两机器人出发时相距,
由题意,可得=,或=,或,
解得=,或=,或=.
即两机器人出发或或时相距.
26.
【答案】
,
【解答】
解:∵
数轴上表示数的点到原点的是单位长度,
当时,.
当时,;
选.
一次函数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
在圆的面积计算公式中,变量是(
)
A.
B.
C.,
D.,
?
2.
下列关系式中,不是的函数的是(
)
A.
B.
C.
D.
?
3.
如图,已知直线,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;…;按此作法继续下去,则点的坐标为(
)
A.
B.
C.
D.
?
4.
的底边上的高为,当它的底边从变化到时,的面积(????????)
A.从变化到
B.从变化到
C.从变化到
D.从变化到
?5.
笔记本每本元,买本笔记本共支出元,在这个问题中:
①是常量时,是变量;②是变量时,是常量;③是变量时,也是变量;
④,可以都是常量或都是变量.上述判断正确的有(
)
A.个
B.个
C.个
D.个
?
6.
以下是关于常量和变量的说法:
在一个变化过程中,允许出现多个变量和常量;
变量就是变量,它不可以转化为常量;
变量和常量是相对而言的,在一定条件下可以相互转化;
在一个变化过程中,变量只有个,常量可以没有,也可能有多个.
其中正确的说法有(
)
A.个
B.个
C.个
D.个
?
7.
如图,直线分别交、轴于、两点,直线经过点,过作平行与轴的直线交于点,再过作平行与轴的直线交于点,…,依此规律作下去,则点的坐标为(
)
A.
B.
C.
D.
?
8.
某电影院共有排座位,第一排有个座位,后面每一排都比前一排多个座位.那么,每排的座位数与这排的排数的函数关系式为(
)
A.
B.
C.
D..
?
9.
如图,在同一直角坐标系内,直线,和的位置可能是?
?
?
?
A.
B.
C.
D.
?
10.
弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的重量间有下面的关系:
下列说法不正确的是(
)
A.与都是变量,且是自变量,是因变量
B.物体质量每增加,弹簧长度增加
C.与的关系表达式是
D.所挂物体质量为时,弹簧长度为
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
函数的自变量的取值范围是________.
?
12.
若函数是一次函数,则________.
?
13.
已知函数,那么=________.
?
14.
已知是正比例函数,则的值是________.
?
15.
若关于的函数是一次函数,则________,________.
?
16.
如图所示,某市自来水公司职工养老保险个人月缴费(元)随个人工资(元)的变化情况,则:
(1)小红的妈妈六月份工资为元,该月她个人应缴养老保险________元;
(2)杨总工程师六月份工资为元,该月他个人应缴养老保险________元.
?
17.
有两段长度相等的河渠挖掘任务,分别交给甲、乙两个工程队同时进行挖掘.下图是反映所挖河渠长度(米)与挖掘时间(时)之间关系的部分图象.开挖________小时后,甲队所挖掘河渠的长度开始超过乙队.
?
18.
如图,直线交坐标轴于、两点,则不等式的解集是________.
?19.
我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费(元)与用水量(吨)之间的关系如图所示,若某户居民月份用水吨,则应交水费________元.
?
20.
函数=与=的图象如图所示,这两个函数的交点在轴上,那么、的值都大于零的的取值范围是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
在同一直角坐标系中画出下列一次函数的图象
(1)
(2)
(3)
(4).
?
22.
一列火车以的速度匀速行驶.
写出它行驶的路程与时间之间的函数表达式;
当时,是多少?
?
23.
一辆汽车油箱内有油升,从某地出发,每行驶小时耗油升,若设剩余油量为升,行驶时间为小时,根据以上信息回答下列问题:
(1)开始时,汽车的油量=________升;
(2)在________小时汽车加油,加了________升,写出加油前与之间的关系式________;
(3)这辆汽车行驶小时,剩余油量多少升?
?
24.
为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过时,水费按每立方米元收费,超过时,超过部分每立方米按元收费,设每户每月用水量为,应缴水费为元.
写出与之间的函数表达式;
如果有两户家庭某月份需缴纳水费为元和元时,求这两户家庭这个月的用水量分别是多少?
?
25.
有一科技小组进行了机器人行走性能试验.在试验场地有、、三点顺次在同一笔直的赛道上,甲、乙两机器人分别从、两点同时同向出发,历时
同时到达点,甲机器人前分钟以的速度行走,乙机器人始终以
的速度行走,如图是甲、乙两机器人之间的距离与他们的行走时间之间的函数图象,请结合图象,回答下列问题:
(1)、两点之间的距离是
,、两点之间的距离是
,=
.
(2)求线段所在直线的函数表达式.
(3)设线段轴,直接写出两机器人出发多长时间相距.
?
26.
某工厂有两批数量相同的产品生产任务,分别交给甲、乙两个小组同时进行生产.如图是反映生产数量(件)与生产时间之间关系的部分图象.请解答下列问题:
某工厂有两批数量相同的产品生产任务,分别交给甲、乙两个小组同时进行生产.如图是反映生产数量(件)与生产时间之间关系的部分图象.请解答下列问题:
乙小组生产到?件时,用了________.生产时,甲小组比乙小组多生产了________件;
请你求出:
①甲小组在的时段内,与之间的函数关系式;(直接写出结论)
②乙小组在的时段内,与之间的函数关系式;(直接写出结论)
③生产几小时后,甲小组所生产的数量开始超过乙小组?(要求写出过程)
如果甲小组生产速度不变,乙小组在生产后,生产速度增加到?件,结果两小组同时完成了任务.问甲小组从开始生产到完工所生产的数量为多少件?(要求写出过程)
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
解:在圆的面积计算公式中,变量为,.
故选.
2.
【答案】
C
【解答】
解:在图象,,中,每给一个值,都有个值与它对应,所以,,中是的函数,
在中,给一个正值,有个值与之对应,所以不是的函数.
故选:.
3.
【答案】
C
【解答】
解:∵
点的坐标是,
∴
,
∵
点在直线上,
∴
,
∴
,
∴
,
得出,
∴
,
∴
的坐标是.
故选.
4.
【答案】
B
【解答】
略
5.
【答案】
B
【解答】
解:由题意得:,
此问题中、都是变量,是常量,或,都是常量,则③④,
故选:.
6.
【答案】
B
【解答】
解:在一个变化过程中,允许出现多个变量和常量,对;
错,变量在一定的条件下可以互相转化常量,如中,一定,、就是变量,一定,、就是变量;
变量和常量往往是相对的,在一定的条件下可以互相转化,正确;
错误,在一个变化过程中,变量只有两个,常量不能没有,也可以是多个.
正确的有个,故选:.
7.
【答案】
C
【解答】
解:∵
直线交轴于点,
∴
当时,,即点坐标为,
∵
轴,
∴
点的纵坐标为,设,
∴
,解得;
∴
点的坐标为,即;
∵
轴,
∴
点的横坐标为,设,
∴
,
∴
点的坐标为;
同理,可得,即;
;
,即;
;
,即.
故选.
8.
【答案】
B
【解答】
解:第一排有个座位,
第二排有个座位,
第三排有个座位,
…,
第排有个座位.
故选.
9.
【答案】
B
【解答】
解:由题意知,分三种情况:
、当时,的图象经过第一、二、三象限;的图象随的增大而增大,并且比倾斜程度大,故选项错误;
、当时,的图象经过第一、二、四象限;的图象随的增大而增大,选项正确;
、当时,的图象经过第二、三、四象限,的图象随的增大而减小,但比倾斜程度大,故,选项错误.
故选.
10.
【答案】
C
【解答】
解:、随的增加而增加,是自变量,是因变量,故选项正确;
、物体质量每增加,弹簧长度增加,故选项正确;
、与的关系表达式是,故选项错误;
、由知,则当时,,即所挂物体质量为时,
弹簧长度为,故选项正确;
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:根据题意得:,
解得:.
故答案为:.
12.
【答案】
【解答】
解:∵
函数是一次函数,
∴
,,
∴
.
故答案为:.
13.
【答案】
【解答】
.
14.
【答案】
【解答】
解:∵
是正比例函数,
∴
且,
解得(不合题意,舍去)或
故答案是:.
15.
【答案】
,
【解答】
解:一次函数的定义条件是:、为常数,,自变量次数为,
∴
根据题意,知
,
解得,,
故答案是、.
16.
【答案】
;
(2)轴上所对应的函数图象上的的值为,故答案为.
【解答】
解:(1)轴上所对应的函数图象上的的值为,
(2)轴上所对应的函数图象上的的值为,
17.
【答案】
【解答】
解:因为甲超过乙在小时后,甲的速度一直是:米/时,乙两小时后的速度为:米/时,
设小时时,甲乙所挖的距离相等,
则,
解得.
18.
【答案】
【解答】
解:由图象可以看出,轴下方的函数图象所对应自变量的取值为,
故不等式的解集是.
故答案为:.
19.
【答案】
【解答】
解:将代入得:
,
解得:,
故
将,代入得:
,
解得:,
故解析式为:
把代入,
故答案为:
20.
【答案】
【解答】
根据图示及数据可知,
函数=与轴的交点坐标是,
由图可知=与轴的交点坐标是,
所以、的值都大于零的的取值范围是:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:如图:(1)图象过和;
(2)图象过和;
(3)图象过和;
(4)图象过和.
【解答】
解:如图:(1)图象过和;
(2)图象过和;
(3)图象过和;
(4)图象过和.
22.
【答案】
解:根据题意可得.
当时,
.
【解答】
解:根据题意可得.
当时,
.
23.
【答案】
,,=
这辆汽车行驶小时,剩余油量升
【解答】
开始时,汽车的油量=升;
故答案为:.
在小时汽车加油,加了:=(升),
机动车每小时的耗油量为=(升),
∴
加油前油箱剩余油量与行驶时间的函数关系为=.
故答案为:;;=.
=(升),
答:这辆汽车行驶小时,剩余油量升.
24.
【答案】
解:当时,;
当时,,
即,
所以与之间的函数表达式为
因为,
所以用水量不超过立方米,
所以当时,,解得.
因为,
所以用水量超过立方米,
所以当.时,,解得.
答:这两户家庭这个月的用水量分别为和.
【解答】
解:当时,;
当时,,
即,
所以与之间的函数表达式为
因为,
所以用水量不超过立方米,
所以当时,,解得.
因为,
所以用水量超过立方米,
所以当.时,,解得.
答:这两户家庭这个月的用水量分别为和.
25.
【答案】
由图象可知,、两点之间的距离是米,
甲机器人前分钟的速度为:=(米/分);
即=;
、两点之间的距离是:=.
故答案为:;;;
设线段所在直线的函数解析式为:=,
∵
=,
∴
点的坐标为,
则,
解得,
则线段所在直线的函数解析式为=;
如图,设,.
∵
,,
∴
线段所在直线的函数解析式为=,
∵
,,
∴
线段所在直线的函数解析式为,
设两机器人出发时相距,
由题意,可得=,或=,或,
解得=,或=,或=.
即两机器人出发或或时相距.
【解答】
由图象可知,、两点之间的距离是米,
甲机器人前分钟的速度为:=(米/分);
即=;
、两点之间的距离是:=.
故答案为:;;;
设线段所在直线的函数解析式为:=,
∵
=,
∴
点的坐标为,
则,
解得,
则线段所在直线的函数解析式为=;
如图,设,.
∵
,,
∴
线段所在直线的函数解析式为=,
∵
,,
∴
线段所在直线的函数解析式为,
设两机器人出发时相距,
由题意,可得=,或=,或,
解得=,或=,或=.
即两机器人出发或或时相距.
26.
【答案】
,
【解答】
解:∵
数轴上表示数的点到原点的是单位长度,
当时,.
当时,;
选.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
