二元一次方程组复习
图片预览

文档简介
姜堂中学师生共用讲学稿
年级:七年级 学科:数 学 执笔: 审核:七年级数学组
内容:二元一次方程组复习 课型:复习 时间:2011-5-8
【学习目标:】
1、理解二元一次方程组的概念,掌握代入法,加减法消元法的解题思想与技能。
2、经历探索二元一次方程组的解法以及应用过程体会数学模型思想,发展学生灵活运用有关知识解决问题的能力。
3、培养良好的数学应用意识,认识“化未知为已知”和“化复杂为简单”的化归思想。
【学习重、难点】
1、重点:二元一次方程组的解法以及应用。
2、难点:利用二元一次方程组建模解决实际问题。
一、学前准备:
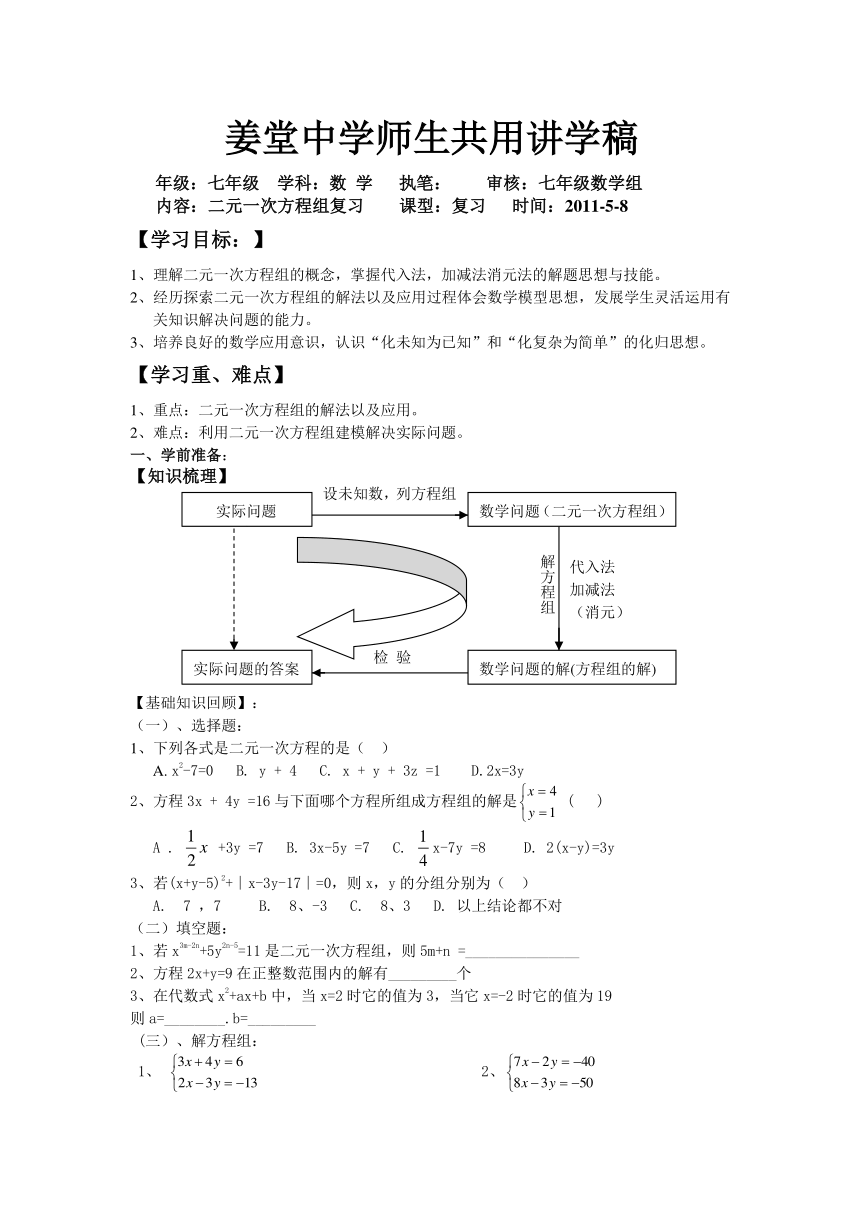
【知识梳理】
【基础知识回顾】:
(一)、选择题:
1、下列各式是二元一次方程的是( )
A. x2-7=0 B. y + 4 C. x + y + 3z =1 D.2x=3y
2、方程3x + 4y =16与下面哪个方程所组成方程组的解是 ( )
A . +3y =7 B. 3x-5y =7 C. x-7y =8 D. 2(x-y)=3y
3、若(x+y-5)2+∣x-3y-17∣=0,则x,y的分组分别为( )
A. 7 ,7 B. 8、-3 C. 8、3 D. 以上结论都不对
(二)填空题:
1、若x3m-2n+5y2n-5=11是二元一次方程组,则5m+n =_______________
2、方程2x+y=9在正整数范围内的解有_________个
3、在代数式x2+ax+b中,当x=2时它的值为3,当它x=-2时它的值为19
则a=________.b=_________
(三)、解方程组:
1、 2、
(四)、复习疑难摘要
二、合作探究:
例1、解方程组
小刚是这样做的:由②得y=4-2x ③,把③代入①得4x+3(4-2x)=6,4x+12-6x=6,-2x=-6,
∴x=3 你认为对吗?为什么?
例2、先阅读材料,然后解方程组。
材料:解方程组
由①得x-y=1 ③
把③代入②,得4×1-y=5
解得y=-1。
把y=-1代入③得x=0。
∴
这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请、用这种方法解方程组
例3、一张方桌由一个桌面和四条桌腿组成,如果1m3木料可制作方桌面50个,或制作桌腿300条,现有5m3木料,请你设计一下,应用多少木料做桌面,用多少木料做桌腿,恰好配成方桌多少张?
方法指导:题中的未知量是制作桌面的木料量和制作桌腿的木料量,相等关系有:
(1)制作桌面和桌腿共用木5m3;
((2)桌面的个数与桌腿的个数之比为1:4,如,如果分别设桌面和桌腿共用多少木料,便可列方程组。
解:
三、自我测试:
1、填空
①把二元一次方程+y=2中的x用含y的式子表示为_________
②写出一个以为解的二元一次方程_____________
③如果2m-3n=2,m+2n=1,则3m-n=_____________
2、解方程组:
3、求适合 ==1的x和y的值。
4、甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50℅的利润定价,乙服装按40℅的利润定价,牵头际出售时,应顾客要求,两件服装均定价的9折出售,这样商店共获利157元,求甲乙两件服装的成本各是多少元?
四、应用与拓展
某商场计划拨款9万元从厂家购进50台电视机,已知该厂生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进其中两种不同的电视机共50台,用去90000,请你研究一下商场的进货方案:
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案?
五、复习体会
1、收获:
2、疑惑:
3、自已需要注意的地方:
4、老师需要注意或改进的地方:
实际问题
数学问题的解(方程组的解)
实际问题的答案
解方程组
代入法
加减法
(消元)
检 验
数学问题(二元一次方程组)
设未知数,列方程组
①
②
①
②
年级:七年级 学科:数 学 执笔: 审核:七年级数学组
内容:二元一次方程组复习 课型:复习 时间:2011-5-8
【学习目标:】
1、理解二元一次方程组的概念,掌握代入法,加减法消元法的解题思想与技能。
2、经历探索二元一次方程组的解法以及应用过程体会数学模型思想,发展学生灵活运用有关知识解决问题的能力。
3、培养良好的数学应用意识,认识“化未知为已知”和“化复杂为简单”的化归思想。
【学习重、难点】
1、重点:二元一次方程组的解法以及应用。
2、难点:利用二元一次方程组建模解决实际问题。
一、学前准备:
【知识梳理】
【基础知识回顾】:
(一)、选择题:
1、下列各式是二元一次方程的是( )
A. x2-7=0 B. y + 4 C. x + y + 3z =1 D.2x=3y
2、方程3x + 4y =16与下面哪个方程所组成方程组的解是 ( )
A . +3y =7 B. 3x-5y =7 C. x-7y =8 D. 2(x-y)=3y
3、若(x+y-5)2+∣x-3y-17∣=0,则x,y的分组分别为( )
A. 7 ,7 B. 8、-3 C. 8、3 D. 以上结论都不对
(二)填空题:
1、若x3m-2n+5y2n-5=11是二元一次方程组,则5m+n =_______________
2、方程2x+y=9在正整数范围内的解有_________个
3、在代数式x2+ax+b中,当x=2时它的值为3,当它x=-2时它的值为19
则a=________.b=_________
(三)、解方程组:
1、 2、
(四)、复习疑难摘要
二、合作探究:
例1、解方程组
小刚是这样做的:由②得y=4-2x ③,把③代入①得4x+3(4-2x)=6,4x+12-6x=6,-2x=-6,
∴x=3 你认为对吗?为什么?
例2、先阅读材料,然后解方程组。
材料:解方程组
由①得x-y=1 ③
把③代入②,得4×1-y=5
解得y=-1。
把y=-1代入③得x=0。
∴
这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请、用这种方法解方程组
例3、一张方桌由一个桌面和四条桌腿组成,如果1m3木料可制作方桌面50个,或制作桌腿300条,现有5m3木料,请你设计一下,应用多少木料做桌面,用多少木料做桌腿,恰好配成方桌多少张?
方法指导:题中的未知量是制作桌面的木料量和制作桌腿的木料量,相等关系有:
(1)制作桌面和桌腿共用木5m3;
((2)桌面的个数与桌腿的个数之比为1:4,如,如果分别设桌面和桌腿共用多少木料,便可列方程组。
解:
三、自我测试:
1、填空
①把二元一次方程+y=2中的x用含y的式子表示为_________
②写出一个以为解的二元一次方程_____________
③如果2m-3n=2,m+2n=1,则3m-n=_____________
2、解方程组:
3、求适合 ==1的x和y的值。
4、甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50℅的利润定价,乙服装按40℅的利润定价,牵头际出售时,应顾客要求,两件服装均定价的9折出售,这样商店共获利157元,求甲乙两件服装的成本各是多少元?
四、应用与拓展
某商场计划拨款9万元从厂家购进50台电视机,已知该厂生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进其中两种不同的电视机共50台,用去90000,请你研究一下商场的进货方案:
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案?
五、复习体会
1、收获:
2、疑惑:
3、自已需要注意的地方:
4、老师需要注意或改进的地方:
实际问题
数学问题的解(方程组的解)
实际问题的答案
解方程组
代入法
加减法
(消元)
检 验
数学问题(二元一次方程组)
设未知数,列方程组
①
②
①
②
