鲁教版数学七年级上2.1探索勾股定理(第2课时)课件
文档属性
| 名称 | 鲁教版数学七年级上2.1探索勾股定理(第2课时)课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 371.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-08 20:55:37 | ||
图片预览





文档简介
(共27张PPT)
2008年北京奥运会会徽
2002年北京国际数学家大会会徽
你目前知道直角三角形有哪些性质?
温故知新
1、两锐角互余,30°角所对的直角边等于斜边的一半。
2、两直角边的平方和等于斜边的平方。
3、面积等于两直角边乘积的一半。
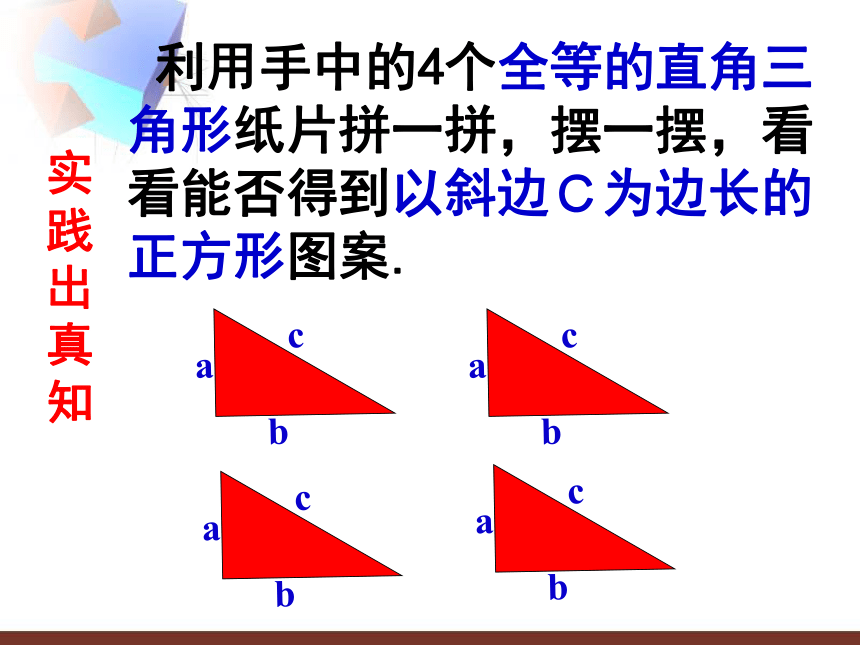
利用手中的4个全等的直角三角形纸片拼一拼,摆一摆,看看能否得到以斜边C为边长的正方形图案.
实践出真知
c
a
b
c
a
b
c
a
b
c
a
b
实践出真知
实践出真知
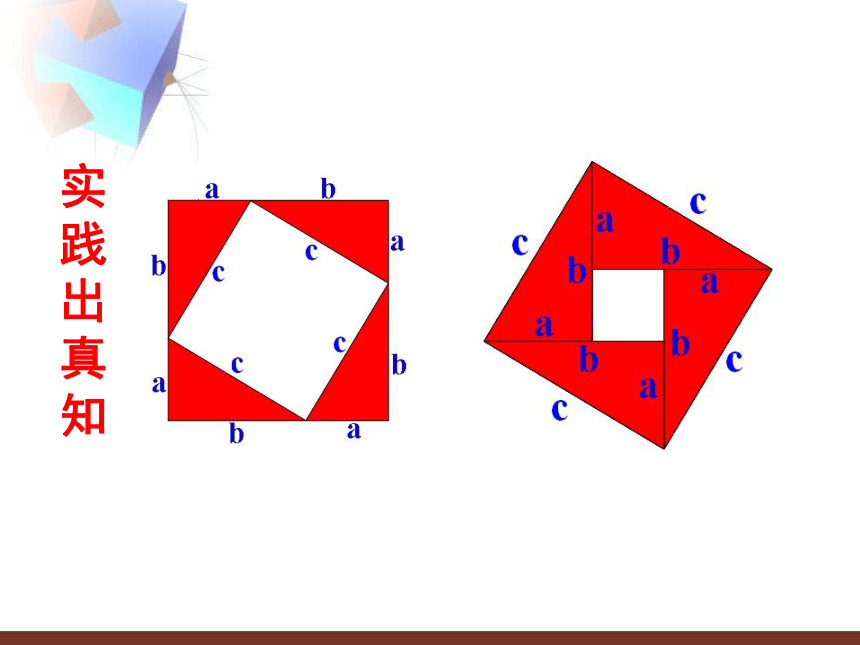
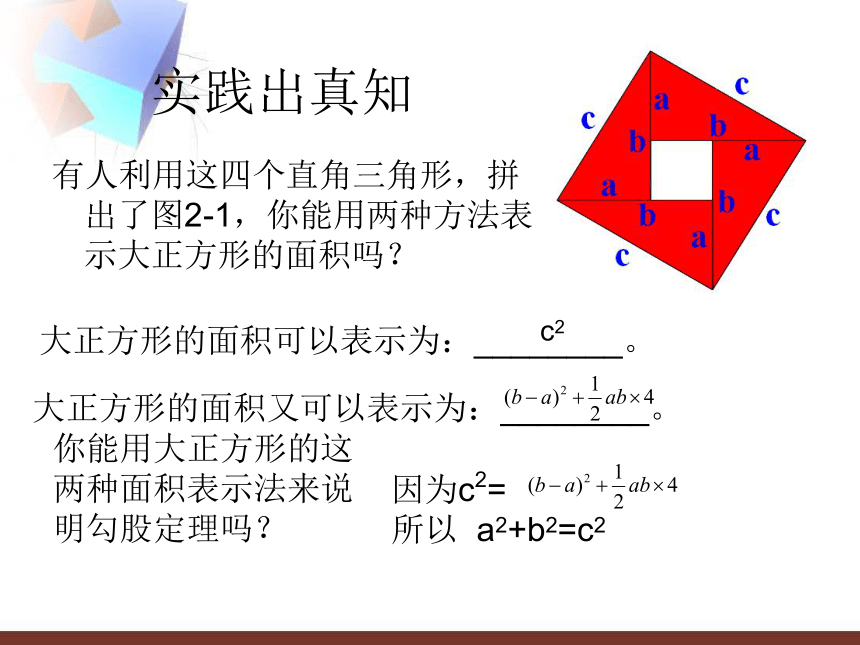
有人利用这四个直角三角形,拼出了图2-1,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为:________。
(a+b)2
大正方形的面积又可以表示为:________。
你能用大正方形的这两种面积表示法来说明勾股定理吗?
因为(a+b)2=
所以 a2+b2=c2
实践出真知
有人利用这四个直角三角形,拼出了图2-1,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为:________。
c2
大正方形的面积又可以表示为:________。
你能用大正方形的这两种面积表示法来说明勾股定理吗?
因为c2=
所以 a2+b2=c2
走进生活
如图2-3,是某公路的示意图,AC⊥BC,AB=1500米,
AC=900米,一辆农用车以18千米/时的速度行驶,那么
它从A直接到B与从A经过C到B相比较可以节约多少时间?
C
B
图2-3
A
分析:在Rt⊿ABC中,由勾股定理得:
______________即____________。
∴BC=__________。
节约的路程为:AC+BC-AB=__________。
农用车的速度为:18千米/时=______米/分。
所以节约的时间为___________。
AC2 +BC2 = AB2
9002+BC2=15002
1200
1200+900-1500=600
300
600÷300=2(分)
猜想开拓
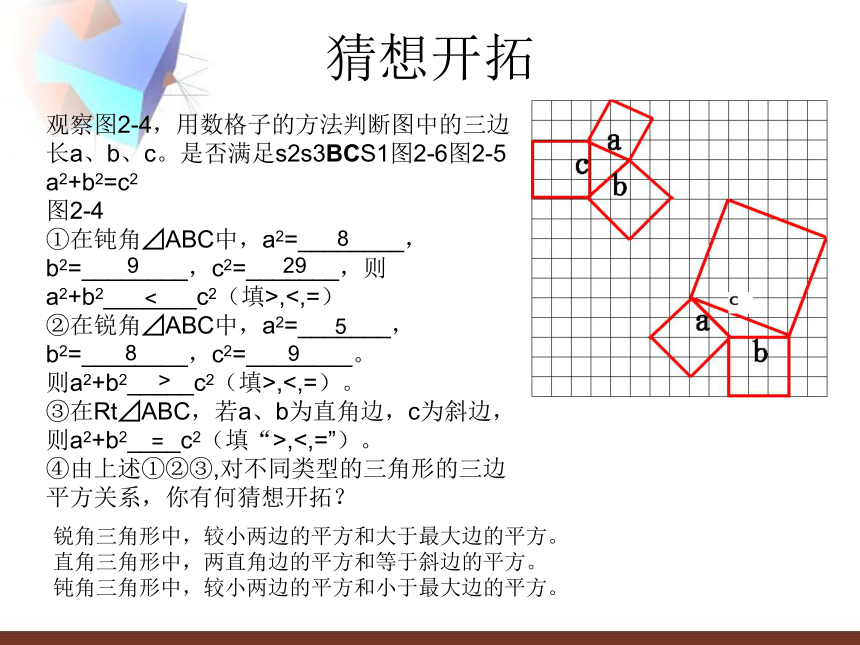
观察图2-4,用数格子的方法判断图中的三边长a、b、c。是否满足s2s3BCS1图2-6图2-5
a2+b2=c2
图2-4 ①在钝角⊿ABC中,a2=________,b2=________,c2=_______,则
a2+b2_______c2(填>,<,=)
②在锐角⊿ABC中,a2=_______,b2=________,c2=________。
则a2+b2_____c2(填>,<,=)。
③在Rt⊿ABC,若a、b为直角边,c为斜边,则a2+b2____c2(填“>,<,=”)。
④由上述①②③,对不同类型的三角形的三边平方关系,你有何猜想开拓?
8
9
29
<
5
8
9
>
=
锐角三角形中,较小两边的平方和大于最大边的平方。
直角三角形中,两直角边的平方和等于斜边的平方。
钝角三角形中,较小两边的平方和小于最大边的平方。
寻找主宰现象的“手”1
s3
s2
S1
①以Rt⊿ABC的三边为边向外作正方形。如图2-5,易知
S1 s2+s3。
=
寻找主宰现象的“手”2
s3
②如图2-6,在⊿ABC中,∠C=90°;分别以AB、AC、BC为之直径向外作半圆,3个半圆的面积分别为s1、s2、s3,求s1、s2、s3、之间的关系。
A
B
C
s1
s2
(
)
S3
S2
S1
AB
8
2
2
1
2
2
1
3
2
8
2
2
1
1
2
2
2
2
2
2
2
2
2
+
=
\
+
=
+
=
÷
è
+
÷
è
=
+
=
÷
è
=
BC
AC
BC
AC
BC
AC
s
s
AB
AB
s
Q
Q
又
p
p
p
p
p
图2-7
寻找主宰现象的“手”3
③在图2-7中,分以⊿ABC三边向外作等边三角形,试猜想s1、s2、s3之间又有何关系?
s
3
s
1
s
2
A
B
C
S1=s2+s3
寻找主宰现象的“手”4
④在图2-5的基础上,以同样的方法继续设计,则s4、s5、s6、s7与s1的关系为
_______________。
S1=S4+S5+S6+S7
s6
s7
s3
s5
s4
s2
s1
寻找主宰现象的“手”5
寻找主宰现象的“手”6
⑤任何现象的背后,都有决定其存在的幕后之“手”!你认为决定图2-5、2-6、2-7、2-8中存在面积特定等量关系的“手”是什么?
勾股定理
寻找主宰现象的“手”7
A
B
C
D
1
4
4
7、“从哪里来,到哪里去?”
一个边长为4的正方形,剪去一个角后,剩下的梯形如图所示
,求这个梯形的周长。
(提示:梯形本由正方形剪角而得,若把梯形恢复为原正方形,可否找到突破的地方?)
E
3
4
分析:在Rt⊿CED中,易求CD=5
∴所求周长为:1+4+4+5=14
直角三角形两条直角边的平方和等于斜边的平方
课堂关键回顾
在△ABC中,如果∠C=90°,
那么a2+b2=c2.
本节通过__________的方法证明了勾股定理的成立
数形结合
下面让我们共同回忆勾股定理的内容
谈谈这节课你学到哪些知识
生活中哪里会用到勾股定理
你获得了哪些经验,还有什么疑惑?
你知道了哪些数学思想和方法?
数学学习日记
作业:
课堂作业:
课本P29习题2.2的第1,2题
课外阅读:
阅读课本P36的课题学习,适当借助互联网资源,继续探索验证勾股定理的方法.
勾股定理
勾股定理:
A
B
C
直角三角形中,两直角边a、b的平方和等于斜边c的平方
即
+ =
在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高这段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理”
在西方,希腊数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了。
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年
相传,毕达哥拉斯学派找到了勾股定理的证明后,欣喜若狂,杀了一百头牛祭神,由此,又有“百牛定理”之称。
公元1945年,人们惊奇地发现了一份古巴比伦人的数学手稿,据考证,其年代远在商高和毕达哥拉斯之前,大致在公元前18世纪。手稿中难以令人置信地列出了15组勾股数,如下表:
序号 勾股数 序号 勾股数
1 119、120、169 9 481、600、769
2 3367、3456、4825 10 4961、6480、8161
3 4601、4800、6649 11 45、60、75
4 12709、13500、 18541 12 1679、2400、2929
5 65、72、97 13 161、240、289
6 319、360、481 14 1771、2700、3229
7 2291、2700、3541 15 56、90、106
8 799、960、1249
这些数,即使在今天也远不是人人都很熟悉,天晓得古巴比伦人当时是怎样弄到这些数的!如果考古学家坚信自己没有弄错历史年代的话,那么上面的史实表明:在世界的其他地方还不知道3、4、5的关系的时期,古巴比伦人就已经有了一个相当灿烂的文化。这无疑给人类早期的文明史,又增添了一个千古之迷!
怎样寻找勾股数:
1、牢记几组常用的勾股数
2、利用公式来推导
X=m2-n2 y=2mn z=m2+n2
(m、n是任意两个正整数,且m>n)
2008年北京奥运会会徽
2002年北京国际数学家大会会徽
你目前知道直角三角形有哪些性质?
温故知新
1、两锐角互余,30°角所对的直角边等于斜边的一半。
2、两直角边的平方和等于斜边的平方。
3、面积等于两直角边乘积的一半。
利用手中的4个全等的直角三角形纸片拼一拼,摆一摆,看看能否得到以斜边C为边长的正方形图案.
实践出真知
c
a
b
c
a
b
c
a
b
c
a
b
实践出真知
实践出真知
有人利用这四个直角三角形,拼出了图2-1,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为:________。
(a+b)2
大正方形的面积又可以表示为:________。
你能用大正方形的这两种面积表示法来说明勾股定理吗?
因为(a+b)2=
所以 a2+b2=c2
实践出真知
有人利用这四个直角三角形,拼出了图2-1,你能用两种方法表示大正方形的面积吗?
大正方形的面积可以表示为:________。
c2
大正方形的面积又可以表示为:________。
你能用大正方形的这两种面积表示法来说明勾股定理吗?
因为c2=
所以 a2+b2=c2
走进生活
如图2-3,是某公路的示意图,AC⊥BC,AB=1500米,
AC=900米,一辆农用车以18千米/时的速度行驶,那么
它从A直接到B与从A经过C到B相比较可以节约多少时间?
C
B
图2-3
A
分析:在Rt⊿ABC中,由勾股定理得:
______________即____________。
∴BC=__________。
节约的路程为:AC+BC-AB=__________。
农用车的速度为:18千米/时=______米/分。
所以节约的时间为___________。
AC2 +BC2 = AB2
9002+BC2=15002
1200
1200+900-1500=600
300
600÷300=2(分)
猜想开拓
观察图2-4,用数格子的方法判断图中的三边长a、b、c。是否满足s2s3BCS1图2-6图2-5
a2+b2=c2
图2-4 ①在钝角⊿ABC中,a2=________,b2=________,c2=_______,则
a2+b2_______c2(填>,<,=)
②在锐角⊿ABC中,a2=_______,b2=________,c2=________。
则a2+b2_____c2(填>,<,=)。
③在Rt⊿ABC,若a、b为直角边,c为斜边,则a2+b2____c2(填“>,<,=”)。
④由上述①②③,对不同类型的三角形的三边平方关系,你有何猜想开拓?
8
9
29
<
5
8
9
>
=
锐角三角形中,较小两边的平方和大于最大边的平方。
直角三角形中,两直角边的平方和等于斜边的平方。
钝角三角形中,较小两边的平方和小于最大边的平方。
寻找主宰现象的“手”1
s3
s2
S1
①以Rt⊿ABC的三边为边向外作正方形。如图2-5,易知
S1 s2+s3。
=
寻找主宰现象的“手”2
s3
②如图2-6,在⊿ABC中,∠C=90°;分别以AB、AC、BC为之直径向外作半圆,3个半圆的面积分别为s1、s2、s3,求s1、s2、s3、之间的关系。
A
B
C
s1
s2
(
)
S3
S2
S1
AB
8
2
2
1
2
2
1
3
2
8
2
2
1
1
2
2
2
2
2
2
2
2
2
+
=
\
+
=
+
=
÷
è
+
÷
è
=
+
=
÷
è
=
BC
AC
BC
AC
BC
AC
s
s
AB
AB
s
Q
Q
又
p
p
p
p
p
图2-7
寻找主宰现象的“手”3
③在图2-7中,分以⊿ABC三边向外作等边三角形,试猜想s1、s2、s3之间又有何关系?
s
3
s
1
s
2
A
B
C
S1=s2+s3
寻找主宰现象的“手”4
④在图2-5的基础上,以同样的方法继续设计,则s4、s5、s6、s7与s1的关系为
_______________。
S1=S4+S5+S6+S7
s6
s7
s3
s5
s4
s2
s1
寻找主宰现象的“手”5
寻找主宰现象的“手”6
⑤任何现象的背后,都有决定其存在的幕后之“手”!你认为决定图2-5、2-6、2-7、2-8中存在面积特定等量关系的“手”是什么?
勾股定理
寻找主宰现象的“手”7
A
B
C
D
1
4
4
7、“从哪里来,到哪里去?”
一个边长为4的正方形,剪去一个角后,剩下的梯形如图所示
,求这个梯形的周长。
(提示:梯形本由正方形剪角而得,若把梯形恢复为原正方形,可否找到突破的地方?)
E
3
4
分析:在Rt⊿CED中,易求CD=5
∴所求周长为:1+4+4+5=14
直角三角形两条直角边的平方和等于斜边的平方
课堂关键回顾
在△ABC中,如果∠C=90°,
那么a2+b2=c2.
本节通过__________的方法证明了勾股定理的成立
数形结合
下面让我们共同回忆勾股定理的内容
谈谈这节课你学到哪些知识
生活中哪里会用到勾股定理
你获得了哪些经验,还有什么疑惑?
你知道了哪些数学思想和方法?
数学学习日记
作业:
课堂作业:
课本P29习题2.2的第1,2题
课外阅读:
阅读课本P36的课题学习,适当借助互联网资源,继续探索验证勾股定理的方法.
勾股定理
勾股定理:
A
B
C
直角三角形中,两直角边a、b的平方和等于斜边c的平方
即
+ =
在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高这段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理”
在西方,希腊数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了。
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年
相传,毕达哥拉斯学派找到了勾股定理的证明后,欣喜若狂,杀了一百头牛祭神,由此,又有“百牛定理”之称。
公元1945年,人们惊奇地发现了一份古巴比伦人的数学手稿,据考证,其年代远在商高和毕达哥拉斯之前,大致在公元前18世纪。手稿中难以令人置信地列出了15组勾股数,如下表:
序号 勾股数 序号 勾股数
1 119、120、169 9 481、600、769
2 3367、3456、4825 10 4961、6480、8161
3 4601、4800、6649 11 45、60、75
4 12709、13500、 18541 12 1679、2400、2929
5 65、72、97 13 161、240、289
6 319、360、481 14 1771、2700、3229
7 2291、2700、3541 15 56、90、106
8 799、960、1249
这些数,即使在今天也远不是人人都很熟悉,天晓得古巴比伦人当时是怎样弄到这些数的!如果考古学家坚信自己没有弄错历史年代的话,那么上面的史实表明:在世界的其他地方还不知道3、4、5的关系的时期,古巴比伦人就已经有了一个相当灿烂的文化。这无疑给人类早期的文明史,又增添了一个千古之迷!
怎样寻找勾股数:
1、牢记几组常用的勾股数
2、利用公式来推导
X=m2-n2 y=2mn z=m2+n2
(m、n是任意两个正整数,且m>n)
