15_积的乘方(2)
图片预览






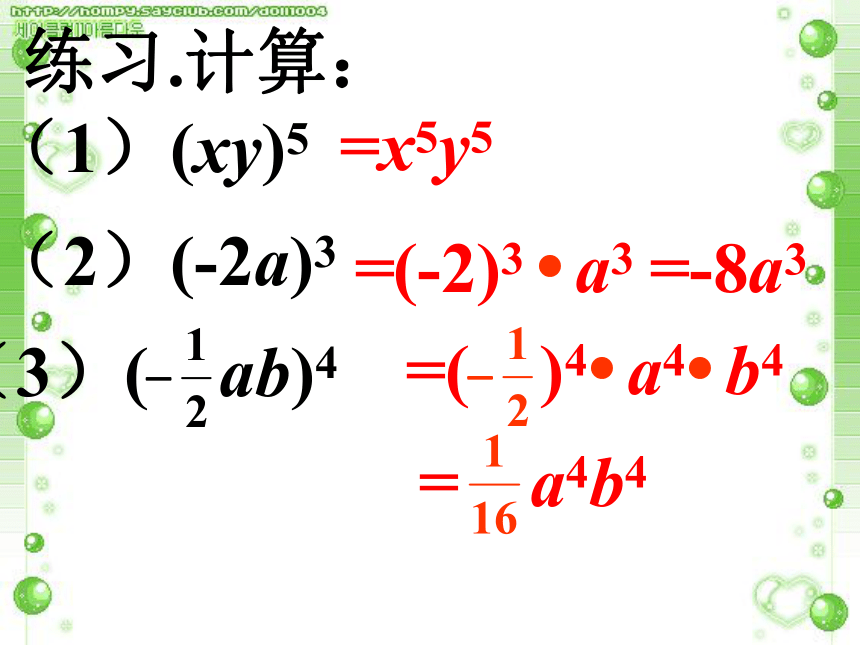

文档简介
(共30张PPT)
13.1.3
实验中学 八年级(1,5)班
回顾与思考
回顾 & 思考
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an
=
am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n= (m、n都是正整数)
amn
知识回顾
填空:
1. am+am=_____,依据________________.
2. a3·a5=____,依据_______________
________.
3. 若am=8,an=30,则am+n=____.
4. (a4)3=_____,依据___________________.
5. (m4)2+m5·m3=____,(a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂乘法的
运算性质
240
a12
幂的乘方的运算性质
2m8
a19
比一比
⑴ (1×2)4=____; 14×24 =_____;
⑵ [3×(-2)]3=_____; 33×(-2)3=_____;
⑶ ( )2= ; = .
16
16
-216
-216
你发现了什么
填空:
1
(ab)n=_____. (n为正整数)
anbn
(ab)n=_____.(n为正整数)
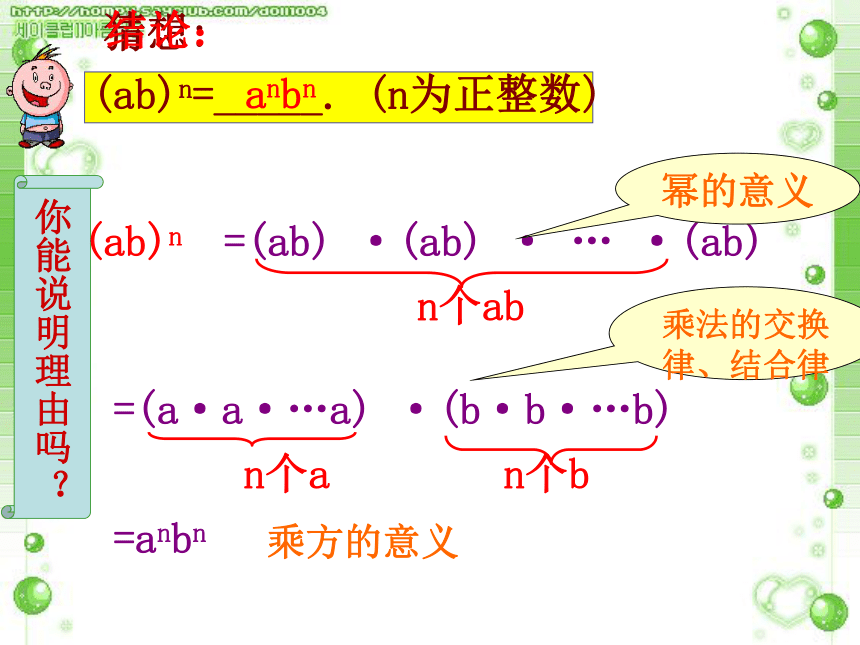
猜想:
你能说明理由吗?
=(ab) ·(ab) · … ·(ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn
(ab)n
幂的意义
乘法的交换律、结合律
乘方的意义
(ab)n=_____. (n为正整数)
anbn
结论:
积的乘方的运算性质:
结论:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
你能用文字语言叙述这个性质吗?
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
例1 计算:
(5m)3 (2)(-xy2)3 (3)(3×103)2
解(5m)3
解(-xy2)3
解:(3×103)2
练习.计算:
(1)(xy)5
(2)(-2a)3
(3)( ab)4
=x5y5
=(-2)3 a3
=-8a3
=( )4 a4 b4
= a4b4
例2 计算:
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.
解: (1) (2a)3=23 a3 = 8a3;
(2) (-5b)3=(-5)3 b3=-125b3;
(3) (xy2)2=x2 (y2)2=x2y4;
(4) (-2x3)4=(-2)4 (x3)4=16x12
1、计算:
(1) (ab)8 (2) (2m)3
(3) (-xy)5 (4) (5ab2)3
(5) (2×102)2 (6) (-3×103)3
答案: (1)a8b8
(2)8m3
(4)125a3b6
(3) –x5y5
(5) 4×104
(6) -27 ×109
1.计算:
(-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3
×
×
x3
4
2.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4 b4 ( )
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
请你推广:
(abc)n =
anbncn
(n为正整数)
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
1
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
(abc)n =
anbncn
(n为正整数)
请你推广:
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
1
(abc)n =
anbncn
(n为正整数)
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
1
(abc)n =
anbncn
(n为正整数)
例2 计算:
(3xy2)2 (2) (2ab3c2)4
解:
(3xy2)2
解:(2ab3c2)4
例3.计算:
(1)(-2a2b)3 (-2a2b)2
(2)(3a3b3)2 - (2a2b2)3
解:(1)(-2a2b)3 (-2a2b)2
= (-2a2b)5
= -32a10b5
(2)(3a3b3)2 - (2a2b2)3
=9a6b6 - 8a6b6
=a6b6
(1)(ab3)2 = ab6
( )
×
( )
×
(ab3)2 = a2b6
(2)(-a2b3)5 = a10b15
(-a2b3)5 = -a10b15
(3)(3a3b2) 3 = 9a9b6
( )
×
(3a3b2) 3 = 27a9b6
( )
×
(4)(a+b)2 = a2+b2
(a+b)2 = a2+2ab+b2
(a+b)2 = a2+2ab+b2
( )
( )
( )
( )
( )
1.在括号里填写适当的计算依据:
(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6
积的乘方的运算性质
积的乘方的运算性质
积的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
3.计算:
⑴ (-a2)3.(-a3)2
⑵ -(n2).(-n5)3
⑶ a5.a3+(2a2)4
⑷ (-2a)3-(-a).(a)2
=1
6个
6个2
解:原式
解:原式
你会计算吗?
试一试
你会计算吗?
知识延伸
逆用积的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
试一试
计算:
解:原式
逆用幂的乘方的运算性质
幂的乘方的运算性质
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
试一试
5.计算:
(1)410 × 0.2510
(3)410 × 0.2511
(2) 5 × 5
看谁本领大!
已知,xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m x2n; (3) x 3m+2n.
解: (1) x m+n=x m x n= ×3= ;
(2) x2m x2n=(x m )2 (x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m x2n=(x m)3 (x n)2=( )3×32
= × 9 =
本节课你的收获是什么?
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an=am+n
幂的乘方运算法则: (ab)n=anbn
积的乘方=
每个因式分别乘方后的积
反向使用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷。
布置作业:
课本21页
1、 2.
课本23页
4
13.1.3
实验中学 八年级(1,5)班
回顾与思考
回顾 & 思考
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an
=
am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n= (m、n都是正整数)
amn
知识回顾
填空:
1. am+am=_____,依据________________.
2. a3·a5=____,依据_______________
________.
3. 若am=8,an=30,则am+n=____.
4. (a4)3=_____,依据___________________.
5. (m4)2+m5·m3=____,(a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂乘法的
运算性质
240
a12
幂的乘方的运算性质
2m8
a19
比一比
⑴ (1×2)4=____; 14×24 =_____;
⑵ [3×(-2)]3=_____; 33×(-2)3=_____;
⑶ ( )2= ; = .
16
16
-216
-216
你发现了什么
填空:
1
(ab)n=_____. (n为正整数)
anbn
(ab)n=_____.(n为正整数)
猜想:
你能说明理由吗?
=(ab) ·(ab) · … ·(ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn
(ab)n
幂的意义
乘法的交换律、结合律
乘方的意义
(ab)n=_____. (n为正整数)
anbn
结论:
积的乘方的运算性质:
结论:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
你能用文字语言叙述这个性质吗?
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
例1 计算:
(5m)3 (2)(-xy2)3 (3)(3×103)2
解(5m)3
解(-xy2)3
解:(3×103)2
练习.计算:
(1)(xy)5
(2)(-2a)3
(3)( ab)4
=x5y5
=(-2)3 a3
=-8a3
=( )4 a4 b4
= a4b4
例2 计算:
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.
解: (1) (2a)3=23 a3 = 8a3;
(2) (-5b)3=(-5)3 b3=-125b3;
(3) (xy2)2=x2 (y2)2=x2y4;
(4) (-2x3)4=(-2)4 (x3)4=16x12
1、计算:
(1) (ab)8 (2) (2m)3
(3) (-xy)5 (4) (5ab2)3
(5) (2×102)2 (6) (-3×103)3
答案: (1)a8b8
(2)8m3
(4)125a3b6
(3) –x5y5
(5) 4×104
(6) -27 ×109
1.计算:
(-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3
×
×
x3
4
2.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4 b4 ( )
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
请你推广:
(abc)n =
anbncn
(n为正整数)
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
1
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
(abc)n =
anbncn
(n为正整数)
请你推广:
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
1
(abc)n =
anbncn
(n为正整数)
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
1
(abc)n =
anbncn
(n为正整数)
例2 计算:
(3xy2)2 (2) (2ab3c2)4
解:
(3xy2)2
解:(2ab3c2)4
例3.计算:
(1)(-2a2b)3 (-2a2b)2
(2)(3a3b3)2 - (2a2b2)3
解:(1)(-2a2b)3 (-2a2b)2
= (-2a2b)5
= -32a10b5
(2)(3a3b3)2 - (2a2b2)3
=9a6b6 - 8a6b6
=a6b6
(1)(ab3)2 = ab6
( )
×
( )
×
(ab3)2 = a2b6
(2)(-a2b3)5 = a10b15
(-a2b3)5 = -a10b15
(3)(3a3b2) 3 = 9a9b6
( )
×
(3a3b2) 3 = 27a9b6
( )
×
(4)(a+b)2 = a2+b2
(a+b)2 = a2+2ab+b2
(a+b)2 = a2+2ab+b2
( )
( )
( )
( )
( )
1.在括号里填写适当的计算依据:
(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6
积的乘方的运算性质
积的乘方的运算性质
积的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
3.计算:
⑴ (-a2)3.(-a3)2
⑵ -(n2).(-n5)3
⑶ a5.a3+(2a2)4
⑷ (-2a)3-(-a).(a)2
=1
6个
6个2
解:原式
解:原式
你会计算吗?
试一试
你会计算吗?
知识延伸
逆用积的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
试一试
计算:
解:原式
逆用幂的乘方的运算性质
幂的乘方的运算性质
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
试一试
5.计算:
(1)410 × 0.2510
(3)410 × 0.2511
(2) 5 × 5
看谁本领大!
已知,xm= ,xn=3.求下列各式的值:
(1)x m+n; (2) x2m x2n; (3) x 3m+2n.
解: (1) x m+n=x m x n= ×3= ;
(2) x2m x2n=(x m )2 (x n)2=( )2×32= × 9 = ;
(3) x 3m+2n=x3m x2n=(x m)3 (x n)2=( )3×32
= × 9 =
本节课你的收获是什么?
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an=am+n
幂的乘方运算法则: (ab)n=anbn
积的乘方=
每个因式分别乘方后的积
反向使用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷。
布置作业:
课本21页
1、 2.
课本23页
4
