人教版九年级下册数学 26.2实际问题与反比例函数 同步练习试卷(Word版含答案)
文档属性
| 名称 | 人教版九年级下册数学 26.2实际问题与反比例函数 同步练习试卷(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 127.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
26.2实际问题与反比例函数
同步练习
一.选择题
1.如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应( )
A.不小于h
B.不大于h
C.不小于h
D.不大于h
2.已知电压U、电流I、电阻R三者之间的关系式为:U=IR(或者I=),实际生活中,由于给定已知量不同,因此会有不同的可能图象,图象不可能是( )
A.
B.
C.
D.
3.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P=(S≠0),这个反比例函数的图象大致是( )
A.
B.
C.
D.
4.已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于m3
B.小于m3
C.不小于m3
D.小于m3
5.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,则动力F(单位:N)关于动力臂L(单位:m)的函数解析式正确的是( )
A.F=
B.F=
C.F=
D.F=
6.甲、乙两地相距100千米,某人开车从甲地到乙地,那么他的速度v(千米/小时)与时间t(小时)之间的函数关系用图象表示大致为( )
A.
B.
C.
D.
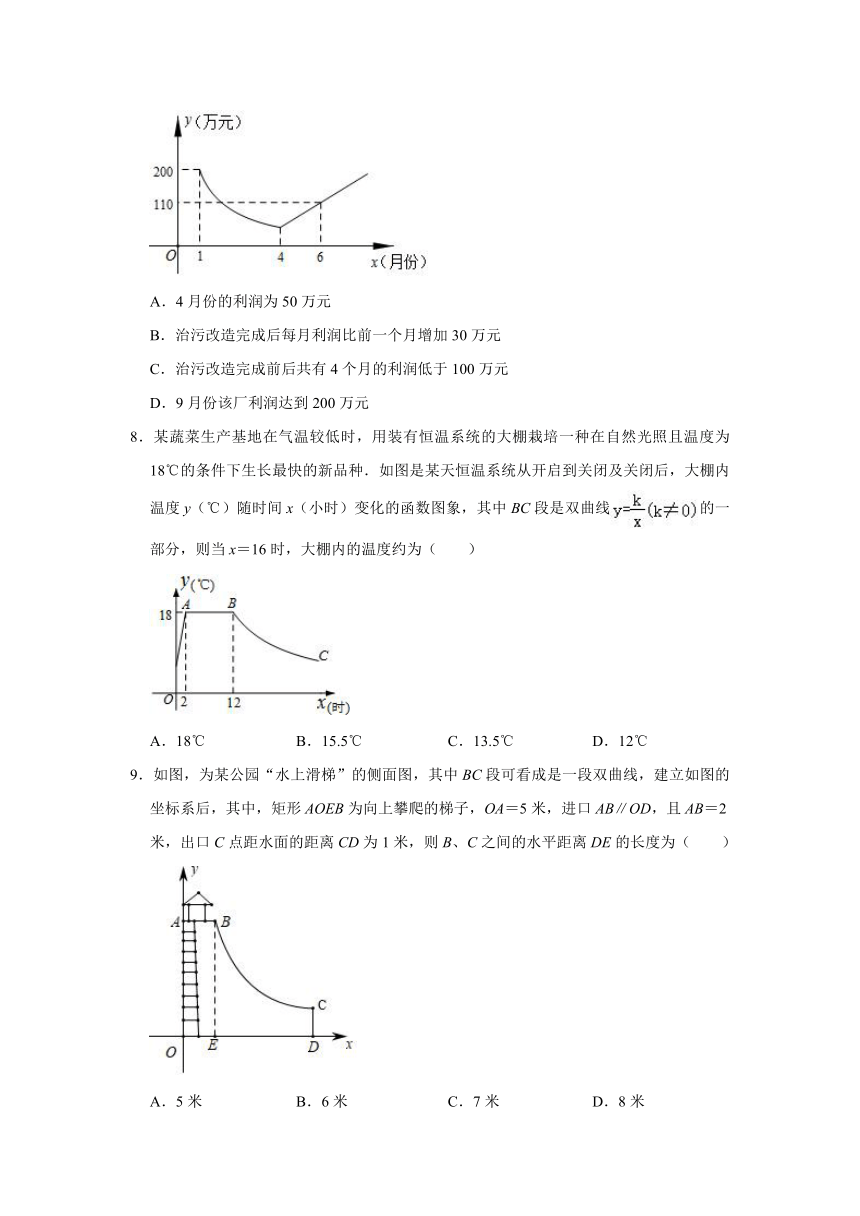
7.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
8.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则当x=16时,大棚内的温度约为( )
A.18℃
B.15.5℃
C.13.5℃
D.12℃
9.如图,为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,建立如图的坐标系后,其中,矩形AOEB为向上攀爬的梯子,OA=5米,进口AB∥OD,且AB=2米,出口C点距水面的距离CD为1米,则B、C之间的水平距离DE的长度为( )
A.5米
B.6米
C.7米
D.8米
10.在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度
y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=(k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
A.18小时
B.17.5小时
C.12小时
D.10小时
二.填空题
11.调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双)
200
240
250
400
销售量y(双)
30
25
24
15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为
元.
12.面积一定的长方形,长为8时宽为5,当长为10时,宽为
.
13.某厂计划建造一个容积为5×104m3的长方体蓄水池,则蓄水池的底面积S(m2)与其深度h(m)的函数关系式是
.
14.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t=
(v>0).
15.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm)…10
15
20
25 30…
y(N)…30
20
15
12 10…
猜测y与x之间的函数关系,并求出函数关系式为
.
三.解答题
16.新冠疫情暴发后,口罩的需求量增大.某口罩加工厂承揽生产1600万个口罩的任务,计划用t天完成.
(1)写出每天生产口罩w(万个)与生产时间t(天)(t>4)之间的函数表达式;
(2)由于国外的疫情形势严峻,卫生管理部门要求厂家提前4天交货,那么加工厂每天要多做多少万个口罩才能完成任务?(用含t的代数式表示)
17.某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升(0≤x≤a)时,满足y=2x,下降时,y与x成反比.
(1)求a的值,并求当a≤x≤8时,y与x的函数表达式;
(2)若血液中药物浓度不低于3微克/毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
18.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.如图,煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系.已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于400℃时,须停止操作.那么锻造的操作时间最多有多长?
(3)如果加工每个零件需要锻造12分钟,并且当材料温度低于400℃时,需要重新煅烧.通过计算说明加工第一个零件,一共需要多少分钟.
参考答案
一.选择题
1.解:设函数解析式为T=,
∵经过点(1,3),
∴k=1×3=3,
∴函数解析式为T=,
当T≤2℃时,t≥h,
故选:C.
2.解:当U一定时,电压U、电流I、电阻R三者之间的关系式为I=,I与R成反比例函数关系,但R不能小于0,所以图象A不可能,B可能;
当R一定时,电压U、电流I、电阻R三者之间的关系式为:U=IR,U和I成正比例函数关系,所以C、D均有可能,
故选:A.
3.解:当F一定时,P与S之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:A.
4.解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=
∵图象过点(1.6,60)
∴k=96
即P=在第一象限内,P随V的增大而减小,
∴当P≤120时,V≥=.
故选:A.
5.解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1500×0.4=FL,
则F=,
故选:C.
6.解:∵甲、乙两地相距100千米,某人开车从甲地到乙地,
∴他的速度v(千米/小时)与时间t(小时)之间的函数关系为:v=(t>0),
则此函数关系用图象表示大致为:
.
故选:D.
7.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
8.解:∵点B(12,18)在双曲线y=上,
∴18=,
解得:k=216.
当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.
故选:C.
9.解:∵四边形AOEB是矩形,
∴BE=OA=5,AB=2,
∴B(2,5),
设双曲线BC的解析式为y=,
∴k=10,
∴y=,
∵CD为1
∴当y=1时,x=10,
∴DE的长=10﹣2=8m,
故选:D.
10.解:把B(12,18)代入y=中得:
k=12×18=216;
设一次函数的解析式为:y=mx+n
把(0,10)、(2,18)代入y=mx+n中,
得:,
解得,
∴AD的解析式为:y=4x+10
当y=12时,12=4x+10,x=0.5,
12=,
解得:x==18,
∴18﹣0.5=17.5,
故选:B.
二.填空题
11.解:由表中数据得:xy=6000,
∴y=,
则所求函数关系式为y=;
由题意得:(x﹣180)y=2400,
把y=代入得:(x﹣180)?=2400,
解得:x=300,
经检验,x=300是原方程的根,
答:若计划每天的销售利润为2400元,则其单价应定为300元.
故答案为:300.
12.解:∵矩形的面积为定值,长为8时,宽为5,
∴矩形的面积为40,
∴设长为y,宽为x,
则y=,
∴当长为10时,宽为:=4.
故答案为:4.
13.解:由题意得:Sh=5×104,
∴S=,
故答案为:S=.
14.解:由录入的时间=录入总量÷录入速度,
可得t=.
故答案为:.
15.解:由图象猜测y与x之间的函数关系为反比例函数,
∴设y=(k≠0),
把x=10,y=30代入得:k=300
∴y=,
将其余各点代入验证均适合,
∴y与x的函数关系式为:y=.
故答案为:y=.
三.解答题
16.解:(1)写出每天生产口罩w(万个)与生产时间t(天)(t>4)之间的函数表达式为:
w=(t>4);
(2)由题意得:w=﹣==(万个),
答:每天要多做(t>4)万个口罩才能完成任务.
17.解:(1)有图象知,a=3;
又由题意可知:当3≤x≤8时,y与x成反比,设.
由图象可知,当x=3时,y=6,
∴m=3×6=18;
∴y=(3≤x≤8);
(2)把y=3分别代入y=2x和y=得,x=1.5和x=6,
∵6﹣1.5=4.5>4,
∴抗菌新药可以作为有效药物投入生产.
18.解:(1)材料锻造时,设y=(k≠0),
由题意得600=,
解得k=4800,
当y=800时,
=800,
解得x=6,
∴点B的坐标为(6,800)
材料煅烧时,设y=ax+32(a≠0),
由题意得800=6a+32,
解得a=128,
∴材料煅烧时,y与x的函数关系式为y=128x+32(0≤x≤6).
∴锻造操作时y与x的函数关系式为y=(x>6);
(2)把y=400代入y=中,得x=12,
12﹣6=6(分),
答:锻造的操作时间6分钟;
(3)当y=800时,即
=800,
∴x=6,
从400升到800需要min,再加上两次6分钟的锻造,加上煅烧的时间,一共是min,
∴锻造每个零件需要煅烧两次共12分钟,
∴加工第一个零件一共需要min.
同步练习
一.选择题
1.如图,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支.当温度T≤2℃时,时间t应( )
A.不小于h
B.不大于h
C.不小于h
D.不大于h
2.已知电压U、电流I、电阻R三者之间的关系式为:U=IR(或者I=),实际生活中,由于给定已知量不同,因此会有不同的可能图象,图象不可能是( )
A.
B.
C.
D.
3.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P=(S≠0),这个反比例函数的图象大致是( )
A.
B.
C.
D.
4.已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于m3
B.小于m3
C.不小于m3
D.小于m3
5.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,则动力F(单位:N)关于动力臂L(单位:m)的函数解析式正确的是( )
A.F=
B.F=
C.F=
D.F=
6.甲、乙两地相距100千米,某人开车从甲地到乙地,那么他的速度v(千米/小时)与时间t(小时)之间的函数关系用图象表示大致为( )
A.
B.
C.
D.
7.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
8.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则当x=16时,大棚内的温度约为( )
A.18℃
B.15.5℃
C.13.5℃
D.12℃
9.如图,为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,建立如图的坐标系后,其中,矩形AOEB为向上攀爬的梯子,OA=5米,进口AB∥OD,且AB=2米,出口C点距水面的距离CD为1米,则B、C之间的水平距离DE的长度为( )
A.5米
B.6米
C.7米
D.8米
10.在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭.大棚内温度
y(℃)随时间x(时)变化的函数图象,其中BC段是函数y=(k>0)图象的一部分.若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
A.18小时
B.17.5小时
C.12小时
D.10小时
二.填空题
11.调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双)
200
240
250
400
销售量y(双)
30
25
24
15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为
元.
12.面积一定的长方形,长为8时宽为5,当长为10时,宽为
.
13.某厂计划建造一个容积为5×104m3的长方体蓄水池,则蓄水池的底面积S(m2)与其深度h(m)的函数关系式是
.
14.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t=
(v>0).
15.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm)…10
15
20
25 30…
y(N)…30
20
15
12 10…
猜测y与x之间的函数关系,并求出函数关系式为
.
三.解答题
16.新冠疫情暴发后,口罩的需求量增大.某口罩加工厂承揽生产1600万个口罩的任务,计划用t天完成.
(1)写出每天生产口罩w(万个)与生产时间t(天)(t>4)之间的函数表达式;
(2)由于国外的疫情形势严峻,卫生管理部门要求厂家提前4天交货,那么加工厂每天要多做多少万个口罩才能完成任务?(用含t的代数式表示)
17.某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升(0≤x≤a)时,满足y=2x,下降时,y与x成反比.
(1)求a的值,并求当a≤x≤8时,y与x的函数表达式;
(2)若血液中药物浓度不低于3微克/毫升的持续时间超过4小时,则称药物治疗有效,请问研发的这种抗菌新药可以作为有效药物投入生产吗?为什么?
18.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.如图,煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系.已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于400℃时,须停止操作.那么锻造的操作时间最多有多长?
(3)如果加工每个零件需要锻造12分钟,并且当材料温度低于400℃时,需要重新煅烧.通过计算说明加工第一个零件,一共需要多少分钟.
参考答案
一.选择题
1.解:设函数解析式为T=,
∵经过点(1,3),
∴k=1×3=3,
∴函数解析式为T=,
当T≤2℃时,t≥h,
故选:C.
2.解:当U一定时,电压U、电流I、电阻R三者之间的关系式为I=,I与R成反比例函数关系,但R不能小于0,所以图象A不可能,B可能;
当R一定时,电压U、电流I、电阻R三者之间的关系式为:U=IR,U和I成正比例函数关系,所以C、D均有可能,
故选:A.
3.解:当F一定时,P与S之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:A.
4.解:设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=
∵图象过点(1.6,60)
∴k=96
即P=在第一象限内,P随V的增大而减小,
∴当P≤120时,V≥=.
故选:A.
5.解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1500N和0.4m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1500×0.4=FL,
则F=,
故选:C.
6.解:∵甲、乙两地相距100千米,某人开车从甲地到乙地,
∴他的速度v(千米/小时)与时间t(小时)之间的函数关系为:v=(t>0),
则此函数关系用图象表示大致为:
.
故选:D.
7.解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
8.解:∵点B(12,18)在双曲线y=上,
∴18=,
解得:k=216.
当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.
故选:C.
9.解:∵四边形AOEB是矩形,
∴BE=OA=5,AB=2,
∴B(2,5),
设双曲线BC的解析式为y=,
∴k=10,
∴y=,
∵CD为1
∴当y=1时,x=10,
∴DE的长=10﹣2=8m,
故选:D.
10.解:把B(12,18)代入y=中得:
k=12×18=216;
设一次函数的解析式为:y=mx+n
把(0,10)、(2,18)代入y=mx+n中,
得:,
解得,
∴AD的解析式为:y=4x+10
当y=12时,12=4x+10,x=0.5,
12=,
解得:x==18,
∴18﹣0.5=17.5,
故选:B.
二.填空题
11.解:由表中数据得:xy=6000,
∴y=,
则所求函数关系式为y=;
由题意得:(x﹣180)y=2400,
把y=代入得:(x﹣180)?=2400,
解得:x=300,
经检验,x=300是原方程的根,
答:若计划每天的销售利润为2400元,则其单价应定为300元.
故答案为:300.
12.解:∵矩形的面积为定值,长为8时,宽为5,
∴矩形的面积为40,
∴设长为y,宽为x,
则y=,
∴当长为10时,宽为:=4.
故答案为:4.
13.解:由题意得:Sh=5×104,
∴S=,
故答案为:S=.
14.解:由录入的时间=录入总量÷录入速度,
可得t=.
故答案为:.
15.解:由图象猜测y与x之间的函数关系为反比例函数,
∴设y=(k≠0),
把x=10,y=30代入得:k=300
∴y=,
将其余各点代入验证均适合,
∴y与x的函数关系式为:y=.
故答案为:y=.
三.解答题
16.解:(1)写出每天生产口罩w(万个)与生产时间t(天)(t>4)之间的函数表达式为:
w=(t>4);
(2)由题意得:w=﹣==(万个),
答:每天要多做(t>4)万个口罩才能完成任务.
17.解:(1)有图象知,a=3;
又由题意可知:当3≤x≤8时,y与x成反比,设.
由图象可知,当x=3时,y=6,
∴m=3×6=18;
∴y=(3≤x≤8);
(2)把y=3分别代入y=2x和y=得,x=1.5和x=6,
∵6﹣1.5=4.5>4,
∴抗菌新药可以作为有效药物投入生产.
18.解:(1)材料锻造时,设y=(k≠0),
由题意得600=,
解得k=4800,
当y=800时,
=800,
解得x=6,
∴点B的坐标为(6,800)
材料煅烧时,设y=ax+32(a≠0),
由题意得800=6a+32,
解得a=128,
∴材料煅烧时,y与x的函数关系式为y=128x+32(0≤x≤6).
∴锻造操作时y与x的函数关系式为y=(x>6);
(2)把y=400代入y=中,得x=12,
12﹣6=6(分),
答:锻造的操作时间6分钟;
(3)当y=800时,即
=800,
∴x=6,
从400升到800需要min,再加上两次6分钟的锻造,加上煅烧的时间,一共是min,
∴锻造每个零件需要煅烧两次共12分钟,
∴加工第一个零件一共需要min.
