三角形的中位线
图片预览





文档简介
(共33张PPT)
动手 发现
活动一
用一张长方形纸你能折出一个等边 三角形吗?
B
A
N
M
C
E
D
F
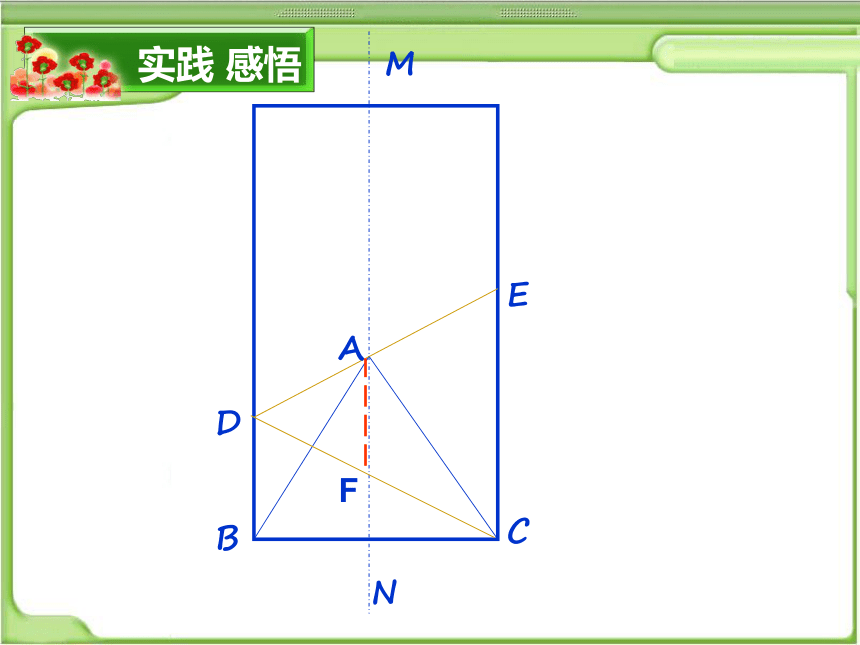
实践 感悟
三角形的中位线
定义: 连接三角形两边中点的线段叫做
三角形的中位线.
新课讲解 想想做做
A
B
C
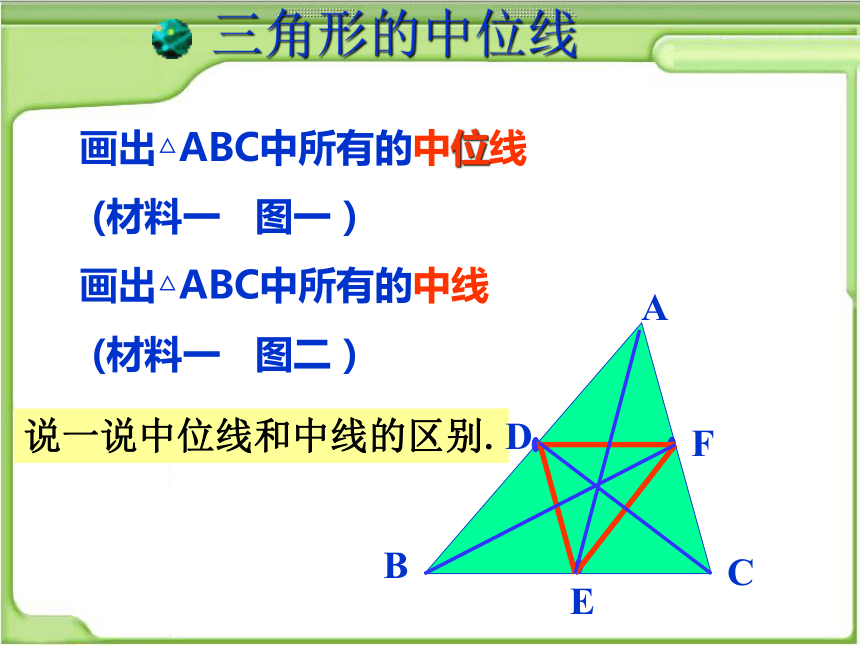
三角形的中位线
画出△ABC中所有的中位线
(材料一 图一)
画出△ABC中所有的中线
(材料一 图二)
说一说中位线和中线的区别.
D
E
F
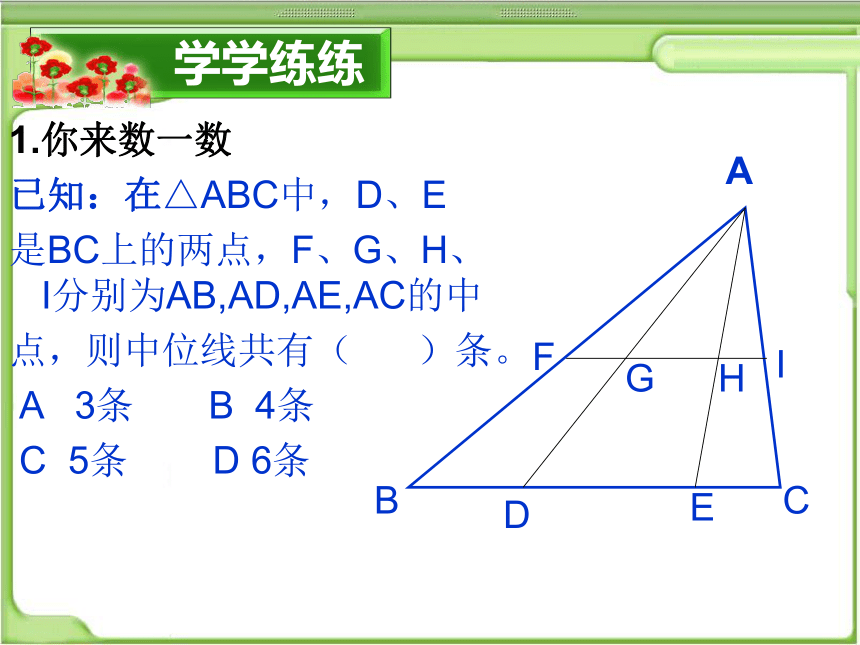
1.你来数一数
已知:在△ABC中,D、E
是BC上的两点,F、G、H、I分别为AB,AD,AE,AC的中
点,则中位线共有( )条。
A 3条 B 4条
C 5条 D 6条
C
B
D
E
F
I
G
H
A
学学练练
B
A
N
M
C
E
D
F
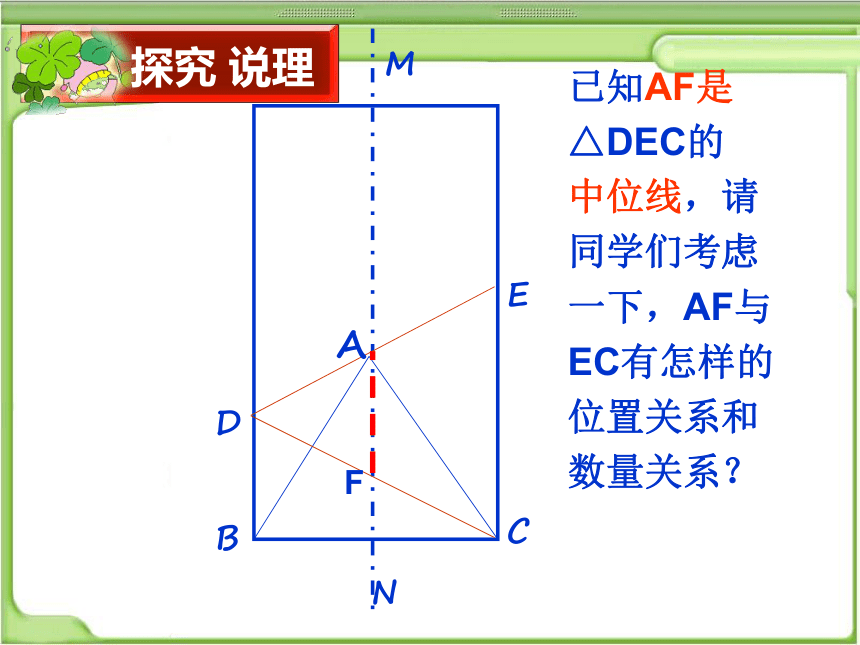
已知AF是
△DEC的
中位线,请
同学们考虑
一下,AF与
EC有怎样的
位置关系和
数量关系?
探究 说理
观察猜想
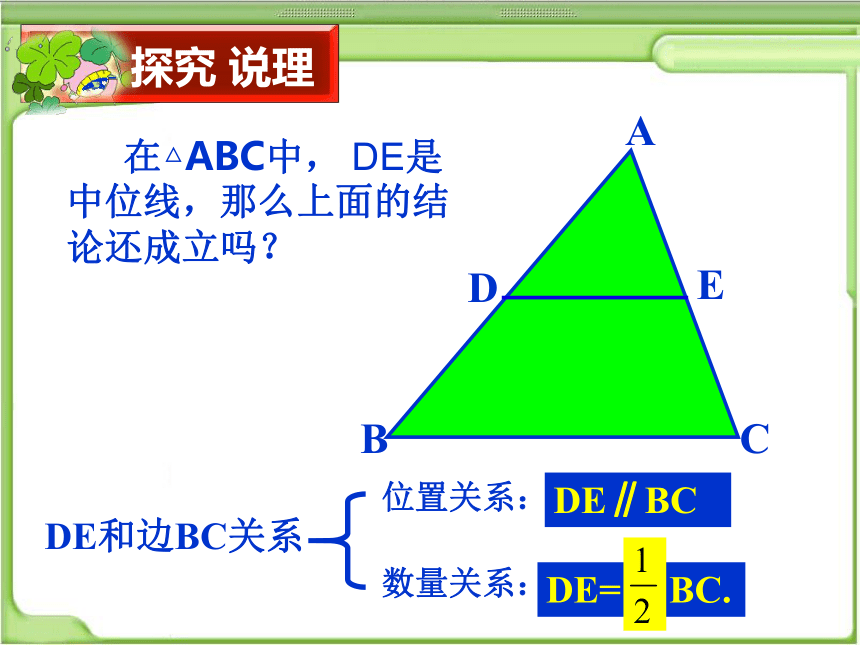
在△ABC中, DE是中位线,那么上面的结论还成立吗?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
DE= BC.
A
B
C
D
E
探究 说理
活动目的:验证三角形的中位线与第三边
的关系
活动要求:
1、先独立思考,然后四人一组,
利用手中的三角形纸片(可
以剪开三角形) ,用尽可能
多的方法进行验证。
2、每组选一位代表讲解。
活动二
B
C
A
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
设计方案
三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
2.你来算一算
已知:在 △ABC中, AB=4cm,AC=6cm,
BC=8cm,D、E、F分别为AB、BC、AC
的中点,则△DEF的周长为 cm
A
B
C
D
E
F
3.你来想一想
已知:等腰三角形边长为1,3则中位线
的长为( )
A B
C 或 D非A、B、C
4.你来切一切
如何帮小明把一块三角形蛋糕切成4
块完全相同的蛋糕?
A
B
A、B两点被池塘隔开无法直接测量,请你设计一个方案,得出A、B两点间的距离。
应用 拓展
A
B
A、B两点被池塘隔开无法直接测量,
请你设计一个方案,得出A、B两点间的距离。
三角形中位线
平行四边形 性质和判定
边
线段间
相等或平行
数量和位置关系
与第三边
请同学们谈一谈你的收获与感悟
交流中共享
转 化
运 用
一边的中点时
作业:
必做题:
1.109页-7题
2.拓展应用整理到作业本上
选做题:122页-16题
做一做
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新四边形的形状有什么特征
H
D
C
B
A
E
F
G
B
C
A
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
设计方案
B
A
N
M
C
D
折纸游戏
(1)先对折长方形纸片
得折痕MN;
(2) 再折纸使折线过C
点且B点落在 MN
上,记为点A;
(3)连接AB、AC, 观察AB,AC和纸片 边缘
BC边所构成的 ABC.
B
A
N
M
C
E
D
P
已知AP是
△DEC的
中位线,请
同学们考虑
一下,AP与
EC有怎样的
位置和数量
关系?
恭喜,胜利了!
三角形中位线
平行四边形 性质和判定
边
线段间
相等或平行
数量和位置关系
与第三边
请同学们谈一谈你的收获与感悟
交流中共享
转 化
运用
一边的中点时
A
B
C
在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.如果测出MN的长,就可知A、B两点的距离?为什么?
M
N
已知:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC
A
B
C
D
E
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
动手 发现
活动一
用一张长方形纸你能折出一个等边 三角形吗?
B
A
N
M
C
E
D
F
实践 感悟
三角形的中位线
定义: 连接三角形两边中点的线段叫做
三角形的中位线.
新课讲解 想想做做
A
B
C
三角形的中位线
画出△ABC中所有的中位线
(材料一 图一)
画出△ABC中所有的中线
(材料一 图二)
说一说中位线和中线的区别.
D
E
F
1.你来数一数
已知:在△ABC中,D、E
是BC上的两点,F、G、H、I分别为AB,AD,AE,AC的中
点,则中位线共有( )条。
A 3条 B 4条
C 5条 D 6条
C
B
D
E
F
I
G
H
A
学学练练
B
A
N
M
C
E
D
F
已知AF是
△DEC的
中位线,请
同学们考虑
一下,AF与
EC有怎样的
位置关系和
数量关系?
探究 说理
观察猜想
在△ABC中, DE是中位线,那么上面的结论还成立吗?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
DE= BC.
A
B
C
D
E
探究 说理
活动目的:验证三角形的中位线与第三边
的关系
活动要求:
1、先独立思考,然后四人一组,
利用手中的三角形纸片(可
以剪开三角形) ,用尽可能
多的方法进行验证。
2、每组选一位代表讲解。
活动二
B
C
A
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
设计方案
三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
2.你来算一算
已知:在 △ABC中, AB=4cm,AC=6cm,
BC=8cm,D、E、F分别为AB、BC、AC
的中点,则△DEF的周长为 cm
A
B
C
D
E
F
3.你来想一想
已知:等腰三角形边长为1,3则中位线
的长为( )
A B
C 或 D非A、B、C
4.你来切一切
如何帮小明把一块三角形蛋糕切成4
块完全相同的蛋糕?
A
B
A、B两点被池塘隔开无法直接测量,请你设计一个方案,得出A、B两点间的距离。
应用 拓展
A
B
A、B两点被池塘隔开无法直接测量,
请你设计一个方案,得出A、B两点间的距离。
三角形中位线
平行四边形 性质和判定
边
线段间
相等或平行
数量和位置关系
与第三边
请同学们谈一谈你的收获与感悟
交流中共享
转 化
运 用
一边的中点时
作业:
必做题:
1.109页-7题
2.拓展应用整理到作业本上
选做题:122页-16题
做一做
如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新四边形的形状有什么特征
H
D
C
B
A
E
F
G
B
C
A
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
设计方案
B
A
N
M
C
D
折纸游戏
(1)先对折长方形纸片
得折痕MN;
(2) 再折纸使折线过C
点且B点落在 MN
上,记为点A;
(3)连接AB、AC, 观察AB,AC和纸片 边缘
BC边所构成的 ABC.
B
A
N
M
C
E
D
P
已知AP是
△DEC的
中位线,请
同学们考虑
一下,AP与
EC有怎样的
位置和数量
关系?
恭喜,胜利了!
三角形中位线
平行四边形 性质和判定
边
线段间
相等或平行
数量和位置关系
与第三边
请同学们谈一谈你的收获与感悟
交流中共享
转 化
运用
一边的中点时
A
B
C
在AB外选一点C,使C能直接到达A和B,连结AC和BC,并分别找出AC和BC的中点M、N.如果测出MN的长,就可知A、B两点的距离?为什么?
M
N
已知:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC
A
B
C
D
E
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
