苏科版九年级下册数学下册7.3: 特殊角的三角函数练习试卷(Word版含答案)
文档属性
| 名称 | 苏科版九年级下册数学下册7.3: 特殊角的三角函数练习试卷(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览

文档简介
锐角三角函数-----特殊角的三角函数
知识点梳理:
一、正弦、余弦、正切复习
∠A的正弦:
∠A的余弦:
∠A的正切:
二、30°、45°、60°角的三角函数值
三角
函数
三角
值
函数
300
450
600
1
例题讲解:
例1、若sinα=,则锐角α=________.若2cosα=1,则锐角α=_________.
例2、若sinα=,则锐角α=_________.若sinα=,则锐角α=_________.
例3、若∠A是锐角,且tanA=,则cosA=_________.
例4、求满足下列条件的锐角α:
(1)cosα-=0
(2)-
tanα+=0
(3)
cosα-2=0
(4)tan(α+10°)=
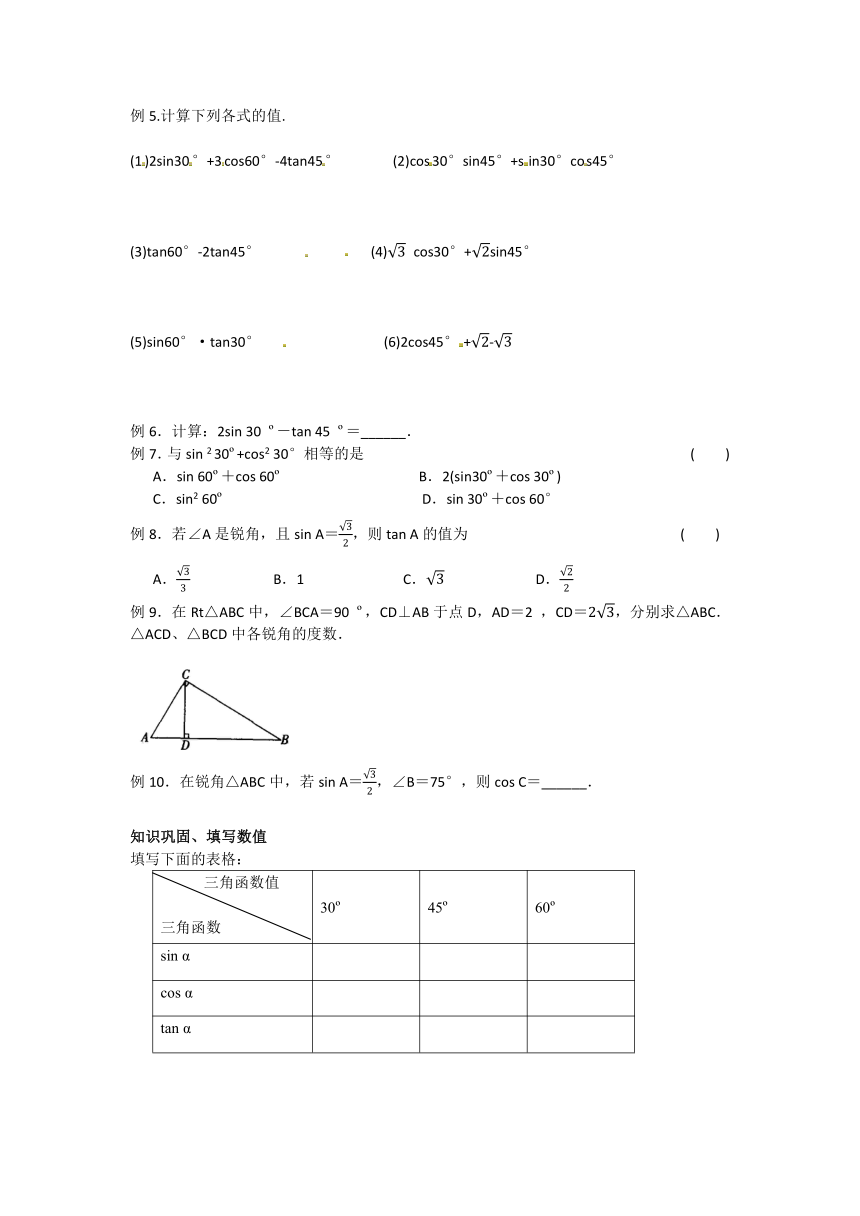
例5.计算下列各式的值.
(1)2sin30°+3cos60°-4tan45°
(2)cos30°sin45°+sin30°cos45°
(3)tan60°-2tan45°
(4)
cos30°+sin45°
(5)sin60°·tan30°
(6)2cos45°+-
例6.计算:2sin
30
?-tan
45
?=______.
例7.与sin
2
30?+cos2
30°相等的是
(
)
A.sin
60?+cos
60?
B.2(sin30?+cos
30?)
C.sin2
60?
D.sin
30?+cos
60°
例8.若∠A是锐角,且sin
A=,则tan
A的值为
(
)
A.
B.1
C.
D.
例9.在Rt△ABC中,∠BCA=90
?,CD⊥AB于点D,AD=2
,CD=,分别求△ABC.
△ACD、△BCD中各锐角的度数.
例10.在锐角△ABC中,若sin
A=,∠B=75°,则cos
C=______.
知识巩固、填写数值
填写下面的表格:
三角函数值
三角函数
30?
45?
60?
sin
α
cos
α
tan
α
巩固练习
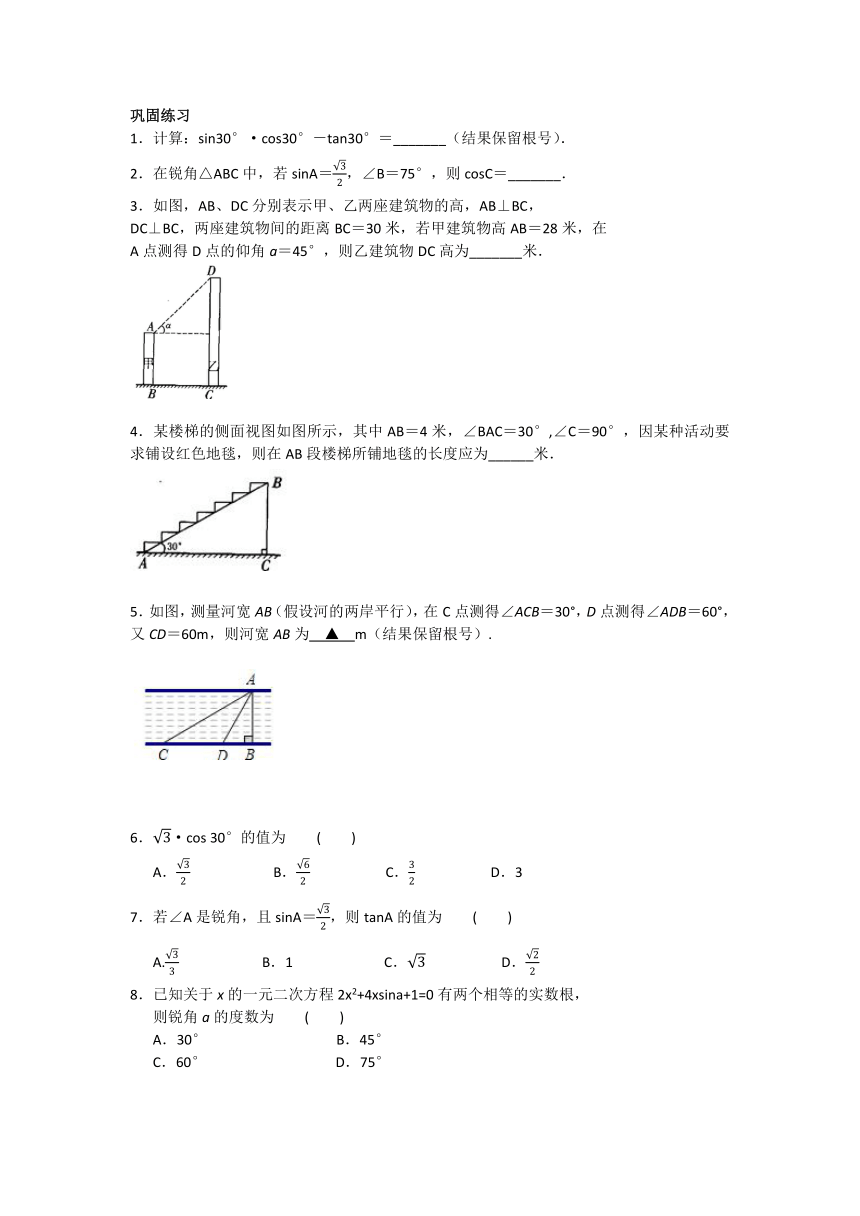
1.计算:sin30°·cos30°-tan30°=_______(结果保留根号).
2.在锐角△ABC中,若sinA=,∠B=75°,则cosC=_______.
3.如图,AB、DC分别表示甲、乙两座建筑物的高,AB⊥BC,
DC⊥BC,两座建筑物间的距离BC=30米,若甲建筑物高AB=28米,在
A点测得D点的仰角a=45°,则乙建筑物DC高为_______米.
4.某楼梯的侧面视图如图所示,其中AB=4米,∠BAC=30°,∠C=90°,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为______米.
5.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为
▲
m(结果保留根号).
6.·cos
30°的值为
(
)
A.
B.
C.
D.3
7.若∠A是锐角,且sinA=,则tanA的值为
(
)
A.
B.1
C.
D.
8.已知关于x的一元二次方程2x2+4xsina+1=0有两个相等的实数根,
则锐角a的度数为
(
)
A.30°
B.45°
C.60°
D.75°
9.关于x的一元二次方程2x2+4xsina+1=0有两个相等的实数根,则锐角α的度数为(
)
A.30°
B.45°
C.60°
D.75°
10.若∠A=38°,则cos
A的大致范围是
(
)
A.0<cos
A<1
B.
C.
D.
11.计算下面各式的值:
(1)
sin45°cos60°-sin60°tan60°;
(2).
12.如图,在Rt△ABC中,∠BCA=
90°,CD⊥AB,AD=2,CD=2,分别求出△ABC、△ACD、△BCD中各个锐角的度数.
13.先化简,再求代数式的值,其中x=2cos
45°-3.
14.已知a是锐角,且sin(a+15°)=,计算-4cos
a-(7π-3.14)0+tan
a+的值.
15.如图,小明家在A处,门前有一个池塘,隔着池塘有一条公路l,AB是A到l的一条小路,现新修一条路AC到公路l.小明测量出∠ACD=
30°,∠ABD=45°,BC=50
m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1
m,≈1.732).
16.如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
(1)求证:△BDQ≌△ADP.
(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).
17.如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于点E.
(l)若△ABD是等边三角形,求DE的长.
(2)若BD=AB,且tan∠HDB=,求DE的长.
18.如图,一次函数y=kx+b的图象经过A(-2,-1)、B(1,3)两点,并且交x轴于点C,交y轴于点D.
(l)求该一次函数的关系式.
(2)求tan∠OCD的值.
(3)求证:∠AOB=135°.
巩固练习答案
1.- 2.
3.58
4.
5.30.
6.C
7.C
8.B
9.B
10.C
11.(1)
(2)
12.∠A=∠BCD=60°,∠B=∠ACD=30°
13.原式=,
14.3
15.≈68.3
16.(1)
略
(2)
17.(1)
DE=
(2)
DE=4
18.(1)
(2)
tan∠OCD=
(3)
∠AOB=135?
知识点梳理:
一、正弦、余弦、正切复习
∠A的正弦:
∠A的余弦:
∠A的正切:
二、30°、45°、60°角的三角函数值
三角
函数
三角
值
函数
300
450
600
1
例题讲解:
例1、若sinα=,则锐角α=________.若2cosα=1,则锐角α=_________.
例2、若sinα=,则锐角α=_________.若sinα=,则锐角α=_________.
例3、若∠A是锐角,且tanA=,则cosA=_________.
例4、求满足下列条件的锐角α:
(1)cosα-=0
(2)-
tanα+=0
(3)
cosα-2=0
(4)tan(α+10°)=
例5.计算下列各式的值.
(1)2sin30°+3cos60°-4tan45°
(2)cos30°sin45°+sin30°cos45°
(3)tan60°-2tan45°
(4)
cos30°+sin45°
(5)sin60°·tan30°
(6)2cos45°+-
例6.计算:2sin
30
?-tan
45
?=______.
例7.与sin
2
30?+cos2
30°相等的是
(
)
A.sin
60?+cos
60?
B.2(sin30?+cos
30?)
C.sin2
60?
D.sin
30?+cos
60°
例8.若∠A是锐角,且sin
A=,则tan
A的值为
(
)
A.
B.1
C.
D.
例9.在Rt△ABC中,∠BCA=90
?,CD⊥AB于点D,AD=2
,CD=,分别求△ABC.
△ACD、△BCD中各锐角的度数.
例10.在锐角△ABC中,若sin
A=,∠B=75°,则cos
C=______.
知识巩固、填写数值
填写下面的表格:
三角函数值
三角函数
30?
45?
60?
sin
α
cos
α
tan
α
巩固练习
1.计算:sin30°·cos30°-tan30°=_______(结果保留根号).
2.在锐角△ABC中,若sinA=,∠B=75°,则cosC=_______.
3.如图,AB、DC分别表示甲、乙两座建筑物的高,AB⊥BC,
DC⊥BC,两座建筑物间的距离BC=30米,若甲建筑物高AB=28米,在
A点测得D点的仰角a=45°,则乙建筑物DC高为_______米.
4.某楼梯的侧面视图如图所示,其中AB=4米,∠BAC=30°,∠C=90°,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为______米.
5.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为
▲
m(结果保留根号).
6.·cos
30°的值为
(
)
A.
B.
C.
D.3
7.若∠A是锐角,且sinA=,则tanA的值为
(
)
A.
B.1
C.
D.
8.已知关于x的一元二次方程2x2+4xsina+1=0有两个相等的实数根,
则锐角a的度数为
(
)
A.30°
B.45°
C.60°
D.75°
9.关于x的一元二次方程2x2+4xsina+1=0有两个相等的实数根,则锐角α的度数为(
)
A.30°
B.45°
C.60°
D.75°
10.若∠A=38°,则cos
A的大致范围是
(
)
A.0<cos
A<1
B.
C.
D.
11.计算下面各式的值:
(1)
sin45°cos60°-sin60°tan60°;
(2).
12.如图,在Rt△ABC中,∠BCA=
90°,CD⊥AB,AD=2,CD=2,分别求出△ABC、△ACD、△BCD中各个锐角的度数.
13.先化简,再求代数式的值,其中x=2cos
45°-3.
14.已知a是锐角,且sin(a+15°)=,计算-4cos
a-(7π-3.14)0+tan
a+的值.
15.如图,小明家在A处,门前有一个池塘,隔着池塘有一条公路l,AB是A到l的一条小路,现新修一条路AC到公路l.小明测量出∠ACD=
30°,∠ABD=45°,BC=50
m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1
m,≈1.732).
16.如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
(1)求证:△BDQ≌△ADP.
(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).
17.如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,D为△ABC外一点,连接AD、BD,过点D作DH⊥AB,垂足为H,交AC于点E.
(l)若△ABD是等边三角形,求DE的长.
(2)若BD=AB,且tan∠HDB=,求DE的长.
18.如图,一次函数y=kx+b的图象经过A(-2,-1)、B(1,3)两点,并且交x轴于点C,交y轴于点D.
(l)求该一次函数的关系式.
(2)求tan∠OCD的值.
(3)求证:∠AOB=135°.
巩固练习答案
1.- 2.
3.58
4.
5.30.
6.C
7.C
8.B
9.B
10.C
11.(1)
(2)
12.∠A=∠BCD=60°,∠B=∠ACD=30°
13.原式=,
14.3
15.≈68.3
16.(1)
略
(2)
17.(1)
DE=
(2)
DE=4
18.(1)
(2)
tan∠OCD=
(3)
∠AOB=135?
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
