苏科版数学八年级上册 3.1 勾股定理 《利用勾股定理解决最短路径问题》教学设计(表格式)
文档属性
| 名称 | 苏科版数学八年级上册 3.1 勾股定理 《利用勾股定理解决最短路径问题》教学设计(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 192.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览

文档简介
《利用勾股定理解决最短路径问题》教学设计
教材分析
本节课是最短路径问题的延续和拓广,不但要寻找最短路径,还要计算其长度。在初中阶段,求解两点之间的距离问题多借助勾股定理进行计算,在中考中占有一定地位.而勾股定理是直角三角形非常重要的性质,有极其广泛的应用。勾股定理指出了直角三角形三边之间的数量关系,是几何图形和数量关系之间的一座桥梁.
学情分析
学生在初一上学期学习线段相关知识时已掌握“同一平面内,两点之间,线段最短”,初二上学期学习轴对称一章时,又接触了最短路径问题,因此对最短路径问题有一定的理解。分类讨论一直都是学生觉得比较难掌握的思想方法,分类不清、分类不全是学生经常犯的错误.
教
学
目
标
知识目标
能运用勾股定理求最短路径问题
能力目标
学会观察图形,勇于探索图形间的关系,培养学生的空间观念;在将实际问题抽象成几何图形过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.
情感目标
通过有趣的问题提高学习数学的兴趣;在解决实际问题的过程中,体验数学学习的实用性,体现人人都学有用的数学,增强自信心,体现成功感.
教学重点
探索、发现立体图形展开成平面图形各种途径,利用勾股定理求最短路径问题.
教学难点
利用数学中的建模思想构造直角三角形,寻找不同路径,利用勾股定理,解决实际问题.
授课类型
新授课
课时:第一课时
教具准备
多媒体课件、三角板、圆柱体、长方体
学具准备
圆柱体、长方体
教学过程
教学环节
教学内容
教学活动
学生活动
设计意图
复习巩固
1.请说一说勾股定理的具体内容
2.两点之间-------最短
3.一个圆柱体的侧面展开图是---------------,它的一边长------------,它的另一边--------
.
4.从行政楼A点走到教学楼B点怎样走最近?
引导学生复习利用勾股定理计算三角形的边长.
引导学生回顾同一平面内,两点之间线段最短的知识.
学生回顾勾股定理和两点之间线段最短的知识.
帮助学生温故知新
合作探究
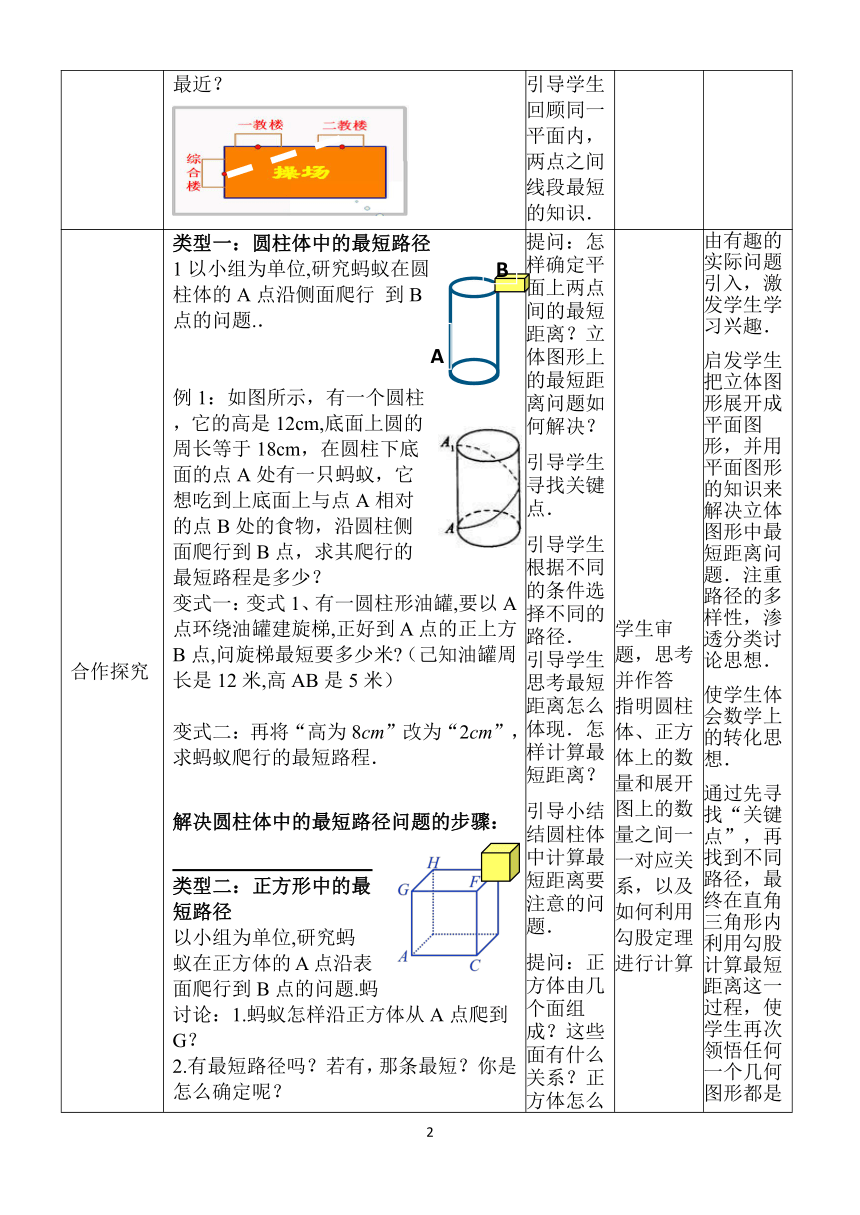
类型一:圆柱体中的最短路径
1以小组为单位,研究蚂蚁在圆
柱体的A点沿侧面爬行
到B
点的问题..
例1:如图所示,有一个圆柱
,它的高是12cm,底面上圆的
周长等于18cm,在圆柱下底
面的点A处有一只蚂蚁,它
想吃到上底面上与点A相对
的点B处的食物,沿圆柱侧
面爬行到B点,求其爬行的
最短路程是多少?
变式一:变式1、有一圆柱形油罐,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问旋梯最短要多少米?(己知油罐周长是12米,高AB是5米)
变式二:再将“高为8cm”改为“2cm”,求蚂蚁爬行的最短路程.
解决圆柱体中的最短路径问题的步骤:
类型二:正方形中的最短路径
以小组为单位,研究蚂蚁在正方体的A点沿表面爬行到B点的问题.蚂
讨论:1.蚂蚁怎样沿正方体从A点爬到G?
2.有最短路径吗?若有,那条最短?你是怎么确定呢?
类型三:长方体中的最短路径
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
小结:解决路径最短问题的依据是
.也就是将曲面或多面体展成一个
面,然后连接需求最短路径的两点,构造
三角形,用勾股定理的数学模型去解决.
解决最短路径问题四部曲
1
.展(立体展平面)
2
.找(找各种路径)
3
.算(算各种路径的长度)
4
.比(比较各种路径的长度)
类型四(拓展提高):与物体表面和内部相关的最短路径
如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离是
.
提问:怎样确定平面上两点间的最短距离?立体图形上的最短距离问题如何解决?
引导学生寻找关键点.
引导学生根据不同的条件选择不同的路径.
引导学生思考最短距离怎么体现.怎样计算最短距离?
引导小结结圆柱体中计算最短距离要注意的问题.
提问:正方体由几个面组成?这些面有什么关系?正方体怎么展开?至少需要展开几个面?
引导学生思考长方体与正方体有何区别?为什么长方体有六种展开方式?(长,宽,高的组合),为什么排除后只有三种?(重复)
引导学生小结解决立体图形上的两点之间最短路径问题的步骤
引导学生将此问题与利用轴寻找最短路径的问题相结合.
学生审题,思考并作答
指明圆柱体、正方体上的数量和展开图上的数量之间一一对应关系,以及如何利用勾股定理进行计算
在教师引导下,学生对六种展开方式分析排除,最终归纳出三种方式计算比较得出最短距离.
总结归纳做题的步骤
将曲线化直线,将此问题转化为利用轴对称解决最短路径问题.
由有趣的实际问题引入,激发学生学习兴趣.
启发学生把立体图形展开成平面图形,并用平面图形的知识来解决立体图形中最短距离问题.注重路径的多样性,渗透分类讨论思想.
使学生体会数学上的转化思想.
通过先寻找“关键点”,再找到不同路径,最终在直角三角形内利用勾股计算最短距离这一过程,使学生再次领悟任何一个几何图形都是由基本元素“点”,“线”,“面”构成,回归几何的本真!
在圆柱体的基础上提升难度,变为正方体,再变为长方体,引导学生由浅入深,认识到要解决立体图形上的最短路径问题一定要将其展开.渗透分类讨论思想.
在初二上学期寻找最短路径的问题上提升到求最短路径长,体现勾股定理是计算线段长的有力手段.
巩固练习
1.如图是一个三级台阶,它的每一级的长、宽、高分别为20cm、3cm、2cm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为
cm.
课后完成
通过配套练习加深学生对本节课所学知识的印象和理解
2.如图,在一个长为2m,宽为1m
的长方形草地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2m的正方形,一只蚂蚁从点A处到达C处需要走的最短路径是
m.
3.一盛满水的圆柱形容器,它的高等于8cm.底面半径等于3cm,在圆柱下底面上的A点有一条小鱼,它想从点A游到点B,小鱼游过的最短路程是多少?
若是蚂蚁想从点A爬到点B,最短路程是多少?(π的值取3)若把圆柱的高改为2cm呢?
4.如图所示,有一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用
秒2.5?
5.如图,长方体盒子(无盖)的长、宽、高分别12cm,8cm,30cm.
(1)在AB中点C处有一滴蜜糖,一只小虫从D处爬到C处去吃,最短路程是多少?
(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?
6.有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80
cm,高AB=60
cm,
水深为AE=40
cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.求小动物爬行的最短路线长?
3至5题
课后完成
教学反思】
①[授课流程反思]
兴趣是最好的老师---学生只有对数学感兴趣,才想学、乐学,最后学会、学好.这就要求老师从“入趣点”着手,通过学生身边熟悉的问题引入,本节课的“入趣点”为“咱们学校”---亲切熟悉的环境,“不走寻常路”---学生中流行的广告词,这样做可以引起学生的情感共鸣,拉近与学生的距离,激发学生的学习兴趣.
②[讲授效果反思]
学生对知识的形成需要一个过程,甚至是几次的反复,本节课知识容量大,如果仅仅将解题过程投放在屏幕上,学生根本来不及思考,所以在教学中板书必不可少,它既能给学生的思维增添时间和空间,又可以规范学生解题的格式.
③[师生互动反思]
1
教材分析
本节课是最短路径问题的延续和拓广,不但要寻找最短路径,还要计算其长度。在初中阶段,求解两点之间的距离问题多借助勾股定理进行计算,在中考中占有一定地位.而勾股定理是直角三角形非常重要的性质,有极其广泛的应用。勾股定理指出了直角三角形三边之间的数量关系,是几何图形和数量关系之间的一座桥梁.
学情分析
学生在初一上学期学习线段相关知识时已掌握“同一平面内,两点之间,线段最短”,初二上学期学习轴对称一章时,又接触了最短路径问题,因此对最短路径问题有一定的理解。分类讨论一直都是学生觉得比较难掌握的思想方法,分类不清、分类不全是学生经常犯的错误.
教
学
目
标
知识目标
能运用勾股定理求最短路径问题
能力目标
学会观察图形,勇于探索图形间的关系,培养学生的空间观念;在将实际问题抽象成几何图形过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.
情感目标
通过有趣的问题提高学习数学的兴趣;在解决实际问题的过程中,体验数学学习的实用性,体现人人都学有用的数学,增强自信心,体现成功感.
教学重点
探索、发现立体图形展开成平面图形各种途径,利用勾股定理求最短路径问题.
教学难点
利用数学中的建模思想构造直角三角形,寻找不同路径,利用勾股定理,解决实际问题.
授课类型
新授课
课时:第一课时
教具准备
多媒体课件、三角板、圆柱体、长方体
学具准备
圆柱体、长方体
教学过程
教学环节
教学内容
教学活动
学生活动
设计意图
复习巩固
1.请说一说勾股定理的具体内容
2.两点之间-------最短
3.一个圆柱体的侧面展开图是---------------,它的一边长------------,它的另一边--------
.
4.从行政楼A点走到教学楼B点怎样走最近?
引导学生复习利用勾股定理计算三角形的边长.
引导学生回顾同一平面内,两点之间线段最短的知识.
学生回顾勾股定理和两点之间线段最短的知识.
帮助学生温故知新
合作探究
类型一:圆柱体中的最短路径
1以小组为单位,研究蚂蚁在圆
柱体的A点沿侧面爬行
到B
点的问题..
例1:如图所示,有一个圆柱
,它的高是12cm,底面上圆的
周长等于18cm,在圆柱下底
面的点A处有一只蚂蚁,它
想吃到上底面上与点A相对
的点B处的食物,沿圆柱侧
面爬行到B点,求其爬行的
最短路程是多少?
变式一:变式1、有一圆柱形油罐,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问旋梯最短要多少米?(己知油罐周长是12米,高AB是5米)
变式二:再将“高为8cm”改为“2cm”,求蚂蚁爬行的最短路程.
解决圆柱体中的最短路径问题的步骤:
类型二:正方形中的最短路径
以小组为单位,研究蚂蚁在正方体的A点沿表面爬行到B点的问题.蚂
讨论:1.蚂蚁怎样沿正方体从A点爬到G?
2.有最短路径吗?若有,那条最短?你是怎么确定呢?
类型三:长方体中的最短路径
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
小结:解决路径最短问题的依据是
.也就是将曲面或多面体展成一个
面,然后连接需求最短路径的两点,构造
三角形,用勾股定理的数学模型去解决.
解决最短路径问题四部曲
1
.展(立体展平面)
2
.找(找各种路径)
3
.算(算各种路径的长度)
4
.比(比较各种路径的长度)
类型四(拓展提高):与物体表面和内部相关的最短路径
如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离是
.
提问:怎样确定平面上两点间的最短距离?立体图形上的最短距离问题如何解决?
引导学生寻找关键点.
引导学生根据不同的条件选择不同的路径.
引导学生思考最短距离怎么体现.怎样计算最短距离?
引导小结结圆柱体中计算最短距离要注意的问题.
提问:正方体由几个面组成?这些面有什么关系?正方体怎么展开?至少需要展开几个面?
引导学生思考长方体与正方体有何区别?为什么长方体有六种展开方式?(长,宽,高的组合),为什么排除后只有三种?(重复)
引导学生小结解决立体图形上的两点之间最短路径问题的步骤
引导学生将此问题与利用轴寻找最短路径的问题相结合.
学生审题,思考并作答
指明圆柱体、正方体上的数量和展开图上的数量之间一一对应关系,以及如何利用勾股定理进行计算
在教师引导下,学生对六种展开方式分析排除,最终归纳出三种方式计算比较得出最短距离.
总结归纳做题的步骤
将曲线化直线,将此问题转化为利用轴对称解决最短路径问题.
由有趣的实际问题引入,激发学生学习兴趣.
启发学生把立体图形展开成平面图形,并用平面图形的知识来解决立体图形中最短距离问题.注重路径的多样性,渗透分类讨论思想.
使学生体会数学上的转化思想.
通过先寻找“关键点”,再找到不同路径,最终在直角三角形内利用勾股计算最短距离这一过程,使学生再次领悟任何一个几何图形都是由基本元素“点”,“线”,“面”构成,回归几何的本真!
在圆柱体的基础上提升难度,变为正方体,再变为长方体,引导学生由浅入深,认识到要解决立体图形上的最短路径问题一定要将其展开.渗透分类讨论思想.
在初二上学期寻找最短路径的问题上提升到求最短路径长,体现勾股定理是计算线段长的有力手段.
巩固练习
1.如图是一个三级台阶,它的每一级的长、宽、高分别为20cm、3cm、2cm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为
cm.
课后完成
通过配套练习加深学生对本节课所学知识的印象和理解
2.如图,在一个长为2m,宽为1m
的长方形草地上,放着一根长方体的木块,它的棱和场地宽AD平行且棱长大于AD,木块从正面看是边长为0.2m的正方形,一只蚂蚁从点A处到达C处需要走的最短路径是
m.
3.一盛满水的圆柱形容器,它的高等于8cm.底面半径等于3cm,在圆柱下底面上的A点有一条小鱼,它想从点A游到点B,小鱼游过的最短路程是多少?
若是蚂蚁想从点A爬到点B,最短路程是多少?(π的值取3)若把圆柱的高改为2cm呢?
4.如图所示,有一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用
秒2.5?
5.如图,长方体盒子(无盖)的长、宽、高分别12cm,8cm,30cm.
(1)在AB中点C处有一滴蜜糖,一只小虫从D处爬到C处去吃,最短路程是多少?
(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?
6.有一个如图示的长方体的透明玻璃鱼缸,假设其长AD=80
cm,高AB=60
cm,
水深为AE=40
cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.求小动物爬行的最短路线长?
3至5题
课后完成
教学反思】
①[授课流程反思]
兴趣是最好的老师---学生只有对数学感兴趣,才想学、乐学,最后学会、学好.这就要求老师从“入趣点”着手,通过学生身边熟悉的问题引入,本节课的“入趣点”为“咱们学校”---亲切熟悉的环境,“不走寻常路”---学生中流行的广告词,这样做可以引起学生的情感共鸣,拉近与学生的距离,激发学生的学习兴趣.
②[讲授效果反思]
学生对知识的形成需要一个过程,甚至是几次的反复,本节课知识容量大,如果仅仅将解题过程投放在屏幕上,学生根本来不及思考,所以在教学中板书必不可少,它既能给学生的思维增添时间和空间,又可以规范学生解题的格式.
③[师生互动反思]
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
