北师大版九年级数学下册 第三章 圆 单元检测试题(Word版 有答案)
文档属性
| 名称 | 北师大版九年级数学下册 第三章 圆 单元检测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 200.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 09:44:52 | ||
图片预览

文档简介
1049020010693400123190000第三章 圆 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列说法正确的有( )
A.优弧的长一定大于劣弧的长
B.以圆心为端点的线段是半径
C.半径相等的两个半圆是等弧
D.不同的圆中,就不可能有相等的弦长
?
2. 下列说法正确的是(? ? ? ? )
A.半径不相等的圆叫做同心圆
B.优弧一定比劣弧长
C.不同的圆中可能有相等的弦
D.半圆一定比直径长
?
3. 已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
?
4. 如图,PA与⊙O切于点A,PBC是⊙O的割线,如果PB=BC=2,那么PA的长为( )
A.2 B.22 C.4 D.8
?
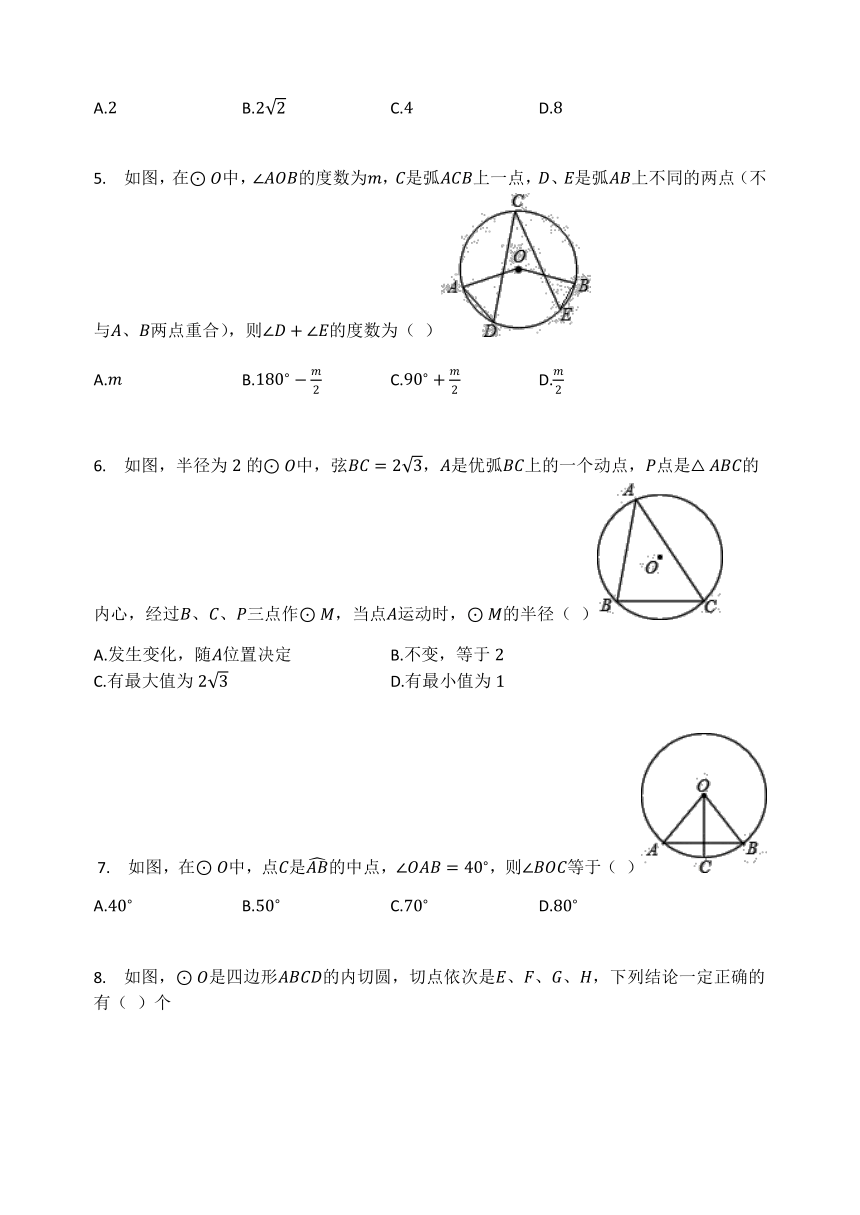
5. 如图,在⊙O中,∠AOB的度数为m,C是弧ACB上一点,D、E是弧AB上不同的两点(不与A、B两点重合),则∠D+∠E的度数为( )
A.m B.180?-m2 C.90?+m2 D.m2
?
6. 如图,半径为2的⊙O中,弦BC=23,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
A.发生变化,随A位置决定 B.不变,等于2
C.有最大值为23 D.有最小值为1
?7. 如图,在⊙O中,点C是AB的中点,∠OAB=40?,则∠BOC等于( )
A.40? B.50? C.70? D.80?
?
8. 如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有( )个
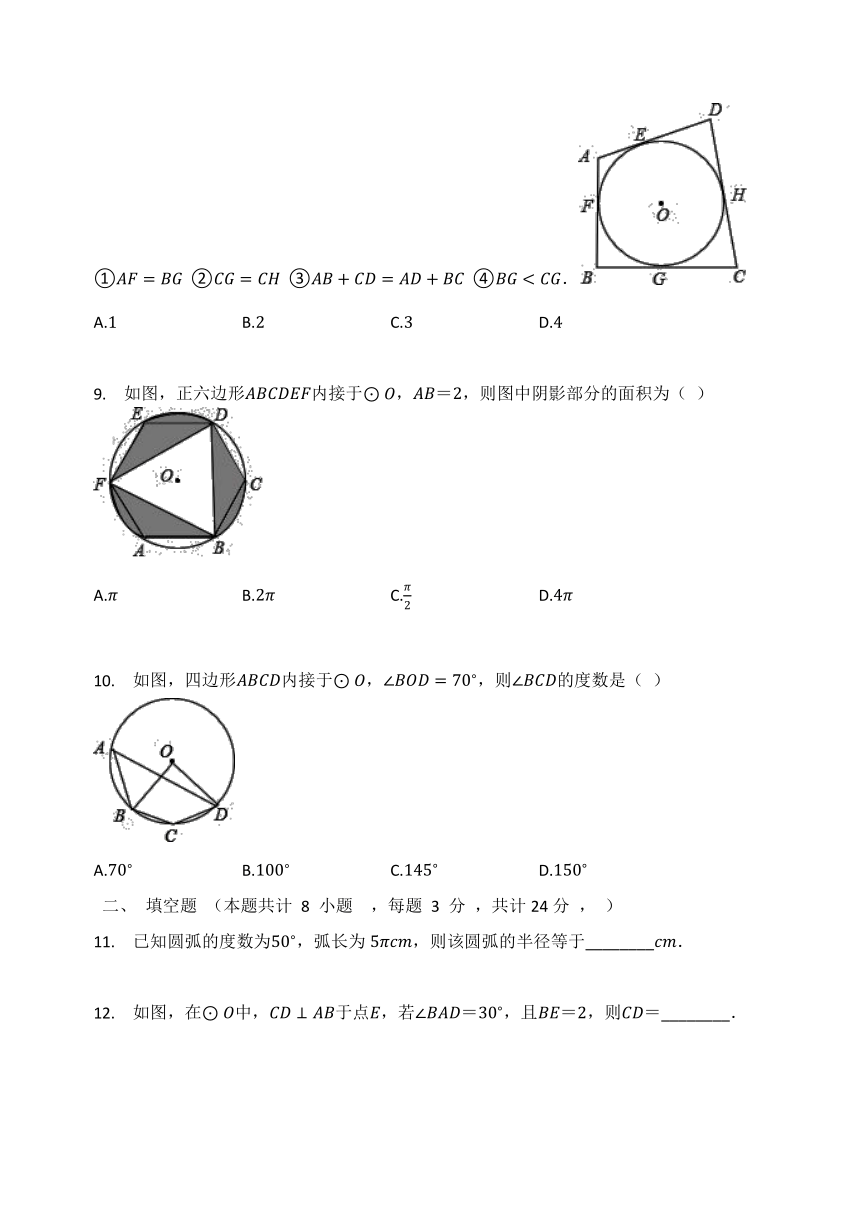
①AF=BG??②CG=CH??③AB+CD=AD+BC??④BG A.1 B.2 C.3 D.4
?
9. 如图,正六边形ABCDEF内接于⊙O,AB=2,则图中阴影部分的面积为( )
A.π B.2π C.π2 D.4π
?
10. 如图,四边形ABCD内接于⊙O,∠BOD=70?,则∠BCD的度数是( )
A.70? B.100? C.145? D.150?
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
11. 已知圆弧的度数为50?,弧长为5πcm,则该圆弧的半径等于________cm.
?
12. 如图,在⊙O中,CD⊥AB于点E,若∠BAD=30?,且BE=2,则CD=________.
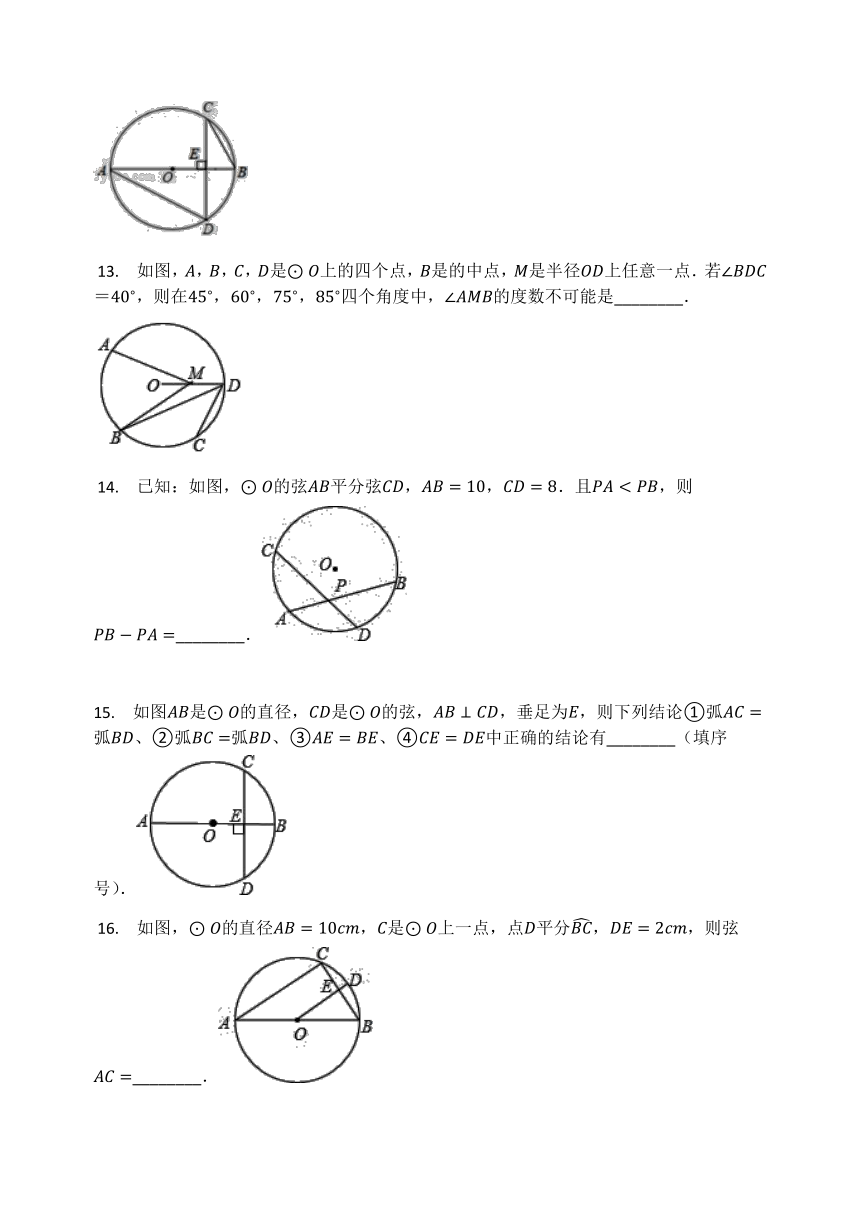
?13. 如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40?,则在45?,60?,75?,85?四个角度中,∠AMB的度数不可能是________.
?14. 已知:如图,⊙O的弦AB平分弦CD,AB=10,CD=8.且PA?
15. 如图AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E,则下列结论①弧AC=弧BD、②弧BC=弧BD、③AE=BE、④CE=DE中正确的结论有________(填序号).
?16. 如图,⊙O的直径AB=10cm,C是⊙O上一点,点D平分BC,DE=2cm,则弦AC=________.
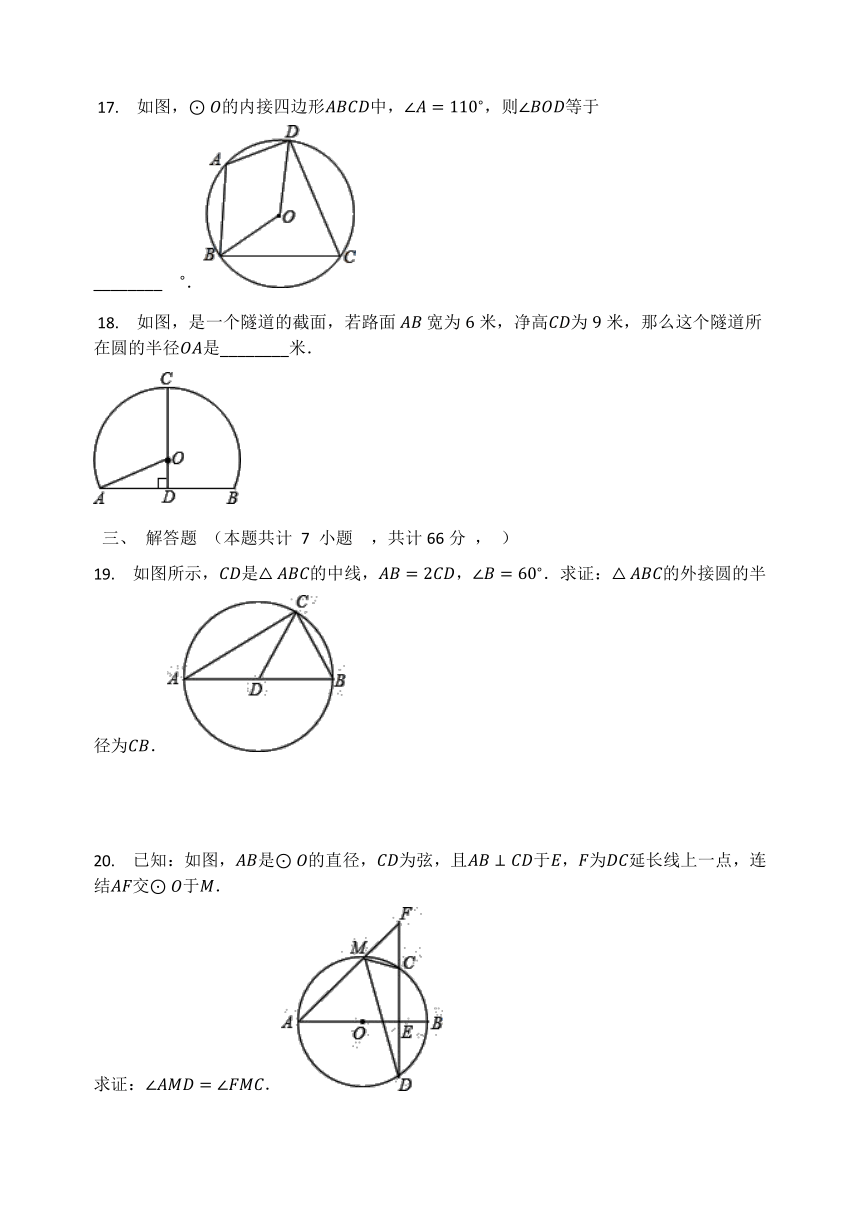
?17. 如图,⊙O的内接四边形ABCD中,∠A=110?,则∠BOD等于________??.
?18. 如图,是一个隧道的截面,若路面?AB?宽为6米,净高CD为9米,那么这个隧道所在圆的半径OA是________米.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 如图所示,CD是△ABC的中线,AB=2CD,∠B=60?.求证:△ABC的外接圆的半径为CB.
?
20. 已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.
求证:∠AMD=∠FMC.
?21. 如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120?
(1)求证:CA=CD
(2)求证:BD=OB.
?
22. 已知在⊙O上,A、B分别为CD,EF的中点,A、B分别交CD、EF于M、N,且AM=BN,证明:CD=EF.
?
23. 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D,E是AC的中点,判断DE与⊙O的位置关系,并说明理由.
?
24. 如图,AB为⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.
(1)求证:PQ是⊙O的切线;
(2)若⊙O的半径为2,TC=3,求弦AD的长.
?
25. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:A、在同圆或等圆中,优弧的长一定大于劣弧的长,所以A选项错误;
B、圆上的点与圆心的连线段是圆的半径,所以B选项错误;
C、半径相等的两个半圆是等弧,所以C选项正确;
D、不同的圆中,可能有相等的弦长,所以D选项错误.
故选C.
2.
【答案】
C
【解答】
解:A,同心圆是指圆心相同但半径不同的圆;
B,在同一个圆中优弧一定大于劣弧,但在不同的圆中不一定;
D,这句话成立的条件是在同一圆中.
故选C.
3.
【答案】
D
【解答】
∵ 点P在⊙O上,
∴ 只需要OP⊥EF即可,
4.
【答案】
B
【解答】
解:∵ PA为⊙O的切线,A为切点,PBC是⊙O的割线,
∴ PA2=PB?PC,
∵ PB=BC=2,
∴ PC=4,
∴ PA2=4×2,
∴ PA=22,
故选B.
5.
【答案】
B
【解答】
解:∵ ∠AOB的度数为m,
∴ 弧AB的度数为m,∴ 弧ACB的度数为360?-m,
∴ ∠D+∠E=12(AC+BC)=(360?-m)÷2=180?-m2.
故选B.
6.
【答案】
B
【解答】
解:作直径BD,连接CD,OC,BM,CM,OM,如图所示:
则∠BCD=90?,∠BAC=∠D,
∴ sinD=BCBD=234=32,
∴ ∠BAC=∠D=60?,
∴ ∠BOC=2∠BAC=120?,∠ABC+∠ACB=120?,
∵ P点是△ABC的内心,
∴ ∠PBC+∠PCB=12(∠ABC+∠ACB)=60?,
∴ ∠BPC=120?=∠BOC,
∴ 点O在⊙M上,
∴ OM=CM,
∵ BM=CM,
∴ BM=CM,
∴ ∠BOM=∠COM=60?,
∴ △OCM是等边三角形,
∴ CM=OC=2,
即⊙M的半径不变,等于2.
故选:B.
7.
【答案】
B
【解答】
解:∵ 点C是AB的中点,
∴ OC⊥AB,
∴ ∠AOC=50?,
∴ ∠BOC=50?.故选B.
8.
【答案】
B
【解答】
解:如图,连接OE、OF、OH、OG.
①∵ ⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,
∴ BF=BG、AF=AE,
只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;
故本选项不一定正确;
②根据题意,知,CG、CH都是⊙O的切线,
∴ CG=CH.
故本选项正确;
③根据题意,知
AF=AE,DH=DE,BF=BG,CG=CH,
则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.
故本选项正确;
④当点G是边BC的中点时,BG=CG.
故本选项错误;
综上所述,正确的说法有2个;
故选B.
9.
【答案】
B
【解答】
如图,连接BO,FO,OA.
由题意得,△OAF,△AOB都是等边三角形,
∴ ∠AOF=∠OAB=60?,
∴ AB?//?OF,
∴ △OAB的面积=△ABF的面积,
∵ 六边形ABCDEF是正六边形,
∴ AF=AB,
∴ 图中阴影部分的面积等于扇形OAB的面积×3=60π×22360×3=2π,
10.
【答案】
C
【解答】
解:∵ ∠A与∠BOD是同弧所对的圆周角与圆心角,∠BOD=70?,
∴ ∠A=12∠BOD=35?.
∵ 四边形ABCD是圆内接四边形,
∴ ∠BCD=180?-∠A=180?-35?=145?.
故选C.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
18
【解答】
解:设该圆弧的半径等于rcm,则
5π=50πr180,
解得t=18.
故答案是:18.
12.
【答案】
43
【解答】
解:∵ ∠BAD=30?,∴ ∠C=∠BAD=30?.
∵ CD⊥AB,
∴ ∠CEB=90?,CD=2CE,BC=2BE=4,
∴ CE=BC2-BE2=42-22=23,
∴ CD=2CE=43.
13.
【答案】
85?
【解答】
∵ B是AC的中点,
∴ ∠AOB=2∠BDC=80?,
又∵ M是OD上一点,
∴ ∠AMB≤∠AOB=80?.
则不符合条件的只有85?.
14.
【答案】
6
【解答】
解:设PB=x,则PA=10-x.由相交弦定理得:PA?PB=PC?PD,即x(10-x)=16
解得:x=2或8,
当x=2时,PB=10-2=8,则PB-PA=8-2=6;
当x=6时,PB=10-6=2<6,不合题意舍去.
故应填6.
15.
【答案】
②④
【解答】
解:∵ AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E,
∴ AB垂直平分CD,
∴ CE=DE,故④正确;
∴ 弧BC=弧BD,故②正确;
∵ AB是⊙O的直径,
∴ AB平分⊙O,
∵ 弧BC=弧BD,
∴ 弧AC=弧AD,故①错误.
∵ CD是⊙O的弦,AB是直径,
∴ AE≠BE,故③错误.
故答案为:②④.
16.
【答案】
6cm
【解答】
解:∵ 点D平分BC,
∴ OD平分BC,
∴ OE为△ABC的中位线,
又∵ ⊙O的直径AB=10cm,
∴ OD=5cm,DE=2cm,
∴ 0E=3cm
则弦AC=6cm.
故答案为6cm.
17.
【答案】
140
【解答】
解:∵ ∠A=110?
∴ ∠C=180?-∠A=70?
∴ ∠BOD=2∠C=140?.
故答案为:140.
18.
【答案】
5
【解答】
因为CD为高,
根据垂径定理:CD平分AB,
又路面AB宽为6米
则有:AD=3?m,
设圆的半径是x米,
在Rt△AOD中,有OA2=AD2+OD2,
即:x2=32+(9-x)2,
解得:x=5,
所以圆的半径长是?5米.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
证明:∵ CD是△ABC的中线,AB=2CD,
∴ AD=BD=CD,
∵ ∠B=60?,
∴ △CDB是等边三角形,
∴ ∠BDC=∠DCB=60?,
∴ ∠A=∠ACD=30?,
∴ ∠ACB=90?,
∴ AB是△ABC的外接圆的直径,
∵ ∠A=30?,∠ACB=90?,
∴ BC=12AB,
∴ △ABC的外接圆的半径为CB.
【解答】
证明:∵ CD是△ABC的中线,AB=2CD,
∴ AD=BD=CD,
∵ ∠B=60?,
∴ △CDB是等边三角形,
∴ ∠BDC=∠DCB=60?,
∴ ∠A=∠ACD=30?,
∴ ∠ACB=90?,
∴ AB是△ABC的外接圆的直径,
∵ ∠A=30?,∠ACB=90?,
∴ BC=12AB,
∴ △ABC的外接圆的半径为CB.
20.
【答案】
证明:连结BM,
∵ AB是⊙O的直径,
∴ ∠AMB=∠BMF=90?,
又∵ AB⊥CD于E,
∴ BC=BD,
∴ ∠CMB=∠BMD,
∴ ∠AMD=∠AMB-∠BMD=∠BMF-∠CMB=∠CMF,
即:∠AMD=∠FMC.
【解答】
证明:连结BM,
∵ AB是⊙O的直径,
∴ ∠AMB=∠BMF=90?,
又∵ AB⊥CD于E,
∴ BC=BD,
∴ ∠CMB=∠BMD,
∴ ∠AMD=∠AMB-∠BMD=∠BMF-∠CMB=∠CMF,
即:∠AMD=∠FMC.
21.
【答案】
(1)证明:
∵ CD切⊙O于点C,
∴ ∠OCD=90?,
∵ ∠ACD=120?,
∴ ∠ACO=30?,
∵ AB是⊙O的直径,
∴ OA=OC=OB,
∴ ∠A=30?,
∴ ∠D=30?,
∴ CA=CD,
(2)∠A=30?,
∴ ∠COB=60?,
∵ CO=BO,
∴ △BOC是等边三角形,
∴ OB=BC,
∵ ∠D=30?,
∴ ∠BCD=∠D=30?,
∴ BD=BC,
∴ BD=OB.
【解答】
(1)证明:
∵ CD切⊙O于点C,
∴ ∠OCD=90?,
∵ ∠ACD=120?,
∴ ∠ACO=30?,
∵ AB是⊙O的直径,
∴ OA=OC=OB,
∴ ∠A=30?,
∴ ∠D=30?,
∴ CA=CD,
(2)∠A=30?,
∴ ∠COB=60?,
∵ CO=BO,
∴ △BOC是等边三角形,
∴ OB=BC,
∵ ∠D=30?,
∴ ∠BCD=∠D=30?,
∴ BD=BC,
∴ BD=OB.
22.
【答案】
证明:∵ A、B分别为CD,EF的中点,
∴ AD=12CD,BE=12EF,
∵ AM=BN,
∴ AD=BE,
∴ CD=EF,
∴ CD=EF.
【解答】
证明:∵ A、B分别为CD,EF的中点,
∴ AD=12CD,BE=12EF,
∵ AM=BN,
∴ AD=BE,
∴ CD=EF,
∴ CD=EF.
23.
【答案】
DE与⊙O相切,
证明:连接OE、OD,
∵ AC是⊙O的切线,
∴ ∠BAC=90?,
∵ OA=OB,AE=EC,
∴ OE?//?BC,
∴ ∠AOE=∠B,∠EOD=∠ODB,
∵ OA=OB,
∴ ∠B=∠ODB,
∴ ∠AOE=∠EOD,
在△AOE和△DOE中,
OA=OD∠AOE=∠DOEOE=OE,
∴ △AOE?△DOE,
∴ ∠ODE=∠BAC=90?,
∴ DE与⊙O相切.
【解答】
此题暂无解答
24.
【答案】
连接OT
∵ OT=OA,
∴ ∠ATO=∠OAT
又∠TAC=∠BAT,
∴ ∠ATO=∠TAC
∴ OT?//?AC
∵ AC⊥PQ,∴ OT⊥PQ,
∴ PQ是⊙O的切线.
过点O作OM⊥AC于M,
则?AM=MD,
又∠OTC=∠ACT=∠OMC=90?,
∴ 四边形OTCM为矩形,
∴ OM=TC=3
在Rt△AOM中,
AM=OA2-OM2=1,
∴ 弦AD的长为2
【解答】
连接OT
∵ OT=OA,
∴ ∠ATO=∠OAT
又∠TAC=∠BAT,
∴ ∠ATO=∠TAC
∴ OT?//?AC
∵ AC⊥PQ,∴ OT⊥PQ,
∴ PQ是⊙O的切线.
过点O作OM⊥AC于M,
则?AM=MD,
又∠OTC=∠ACT=∠OMC=90?,
∴ 四边形OTCM为矩形,
∴ OM=TC=3
在Rt△AOM中,
AM=OA2-OM2=1,
∴ 弦AD的长为2
25.
【答案】
(1)证明见解析;
(2)证明见解析;
(3)CP=16.9cm
【解答】
(1)如图,连接OD,
:BC是○○的直径,
________BAC=90?
AD平分么BAC,
∴ ________BAC=2∠BAD,
BOD=2BAD,
.2BOD=∠BAC=90?
DPIIBC,
.________ODP=∠BOD=90?
….PDLOD,
:OD是○○半径,
…PD是○O的切线;
(2):PDIIBC,
∴ ________ACB=2P
ACB=∠ADB
∴ .ADB=2P
________AB+∠ACD=180? ∴ ACD+∠DCP=180?
________DCP=∠ABD
∴ ΔABD?△DCP;
(3):BC是○○的直径,
∠BDC=∠BAC=90?
在Rt△ABC中,BC=AB2+AC2=13cm
:AD平分么BAC,
∴ 2EAD=∠CAD
∴ 2BOD=∠COD
∴ BD=CE).
在Rt△BCD中,BD2+CD2=BC2
∴ BD=CD=22BC=1322
ΔABD-△DCP
∵ ABCD=BDCP
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列说法正确的有( )
A.优弧的长一定大于劣弧的长
B.以圆心为端点的线段是半径
C.半径相等的两个半圆是等弧
D.不同的圆中,就不可能有相等的弦长
?
2. 下列说法正确的是(? ? ? ? )
A.半径不相等的圆叫做同心圆
B.优弧一定比劣弧长
C.不同的圆中可能有相等的弦
D.半圆一定比直径长
?
3. 已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
?
4. 如图,PA与⊙O切于点A,PBC是⊙O的割线,如果PB=BC=2,那么PA的长为( )
A.2 B.22 C.4 D.8
?
5. 如图,在⊙O中,∠AOB的度数为m,C是弧ACB上一点,D、E是弧AB上不同的两点(不与A、B两点重合),则∠D+∠E的度数为( )
A.m B.180?-m2 C.90?+m2 D.m2
?
6. 如图,半径为2的⊙O中,弦BC=23,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
A.发生变化,随A位置决定 B.不变,等于2
C.有最大值为23 D.有最小值为1
?7. 如图,在⊙O中,点C是AB的中点,∠OAB=40?,则∠BOC等于( )
A.40? B.50? C.70? D.80?
?
8. 如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有( )个
①AF=BG??②CG=CH??③AB+CD=AD+BC??④BG
?
9. 如图,正六边形ABCDEF内接于⊙O,AB=2,则图中阴影部分的面积为( )
A.π B.2π C.π2 D.4π
?
10. 如图,四边形ABCD内接于⊙O,∠BOD=70?,则∠BCD的度数是( )
A.70? B.100? C.145? D.150?
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , ) ?
11. 已知圆弧的度数为50?,弧长为5πcm,则该圆弧的半径等于________cm.
?
12. 如图,在⊙O中,CD⊥AB于点E,若∠BAD=30?,且BE=2,则CD=________.
?13. 如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40?,则在45?,60?,75?,85?四个角度中,∠AMB的度数不可能是________.
?14. 已知:如图,⊙O的弦AB平分弦CD,AB=10,CD=8.且PA
15. 如图AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E,则下列结论①弧AC=弧BD、②弧BC=弧BD、③AE=BE、④CE=DE中正确的结论有________(填序号).
?16. 如图,⊙O的直径AB=10cm,C是⊙O上一点,点D平分BC,DE=2cm,则弦AC=________.
?17. 如图,⊙O的内接四边形ABCD中,∠A=110?,则∠BOD等于________??.
?18. 如图,是一个隧道的截面,若路面?AB?宽为6米,净高CD为9米,那么这个隧道所在圆的半径OA是________米.
三、 解答题 (本题共计 7 小题 ,共计66分 , ) ?
19. 如图所示,CD是△ABC的中线,AB=2CD,∠B=60?.求证:△ABC的外接圆的半径为CB.
?
20. 已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.
求证:∠AMD=∠FMC.
?21. 如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120?
(1)求证:CA=CD
(2)求证:BD=OB.
?
22. 已知在⊙O上,A、B分别为CD,EF的中点,A、B分别交CD、EF于M、N,且AM=BN,证明:CD=EF.
?
23. 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D,E是AC的中点,判断DE与⊙O的位置关系,并说明理由.
?
24. 如图,AB为⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.
(1)求证:PQ是⊙O的切线;
(2)若⊙O的半径为2,TC=3,求弦AD的长.
?
25. 如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:A、在同圆或等圆中,优弧的长一定大于劣弧的长,所以A选项错误;
B、圆上的点与圆心的连线段是圆的半径,所以B选项错误;
C、半径相等的两个半圆是等弧,所以C选项正确;
D、不同的圆中,可能有相等的弦长,所以D选项错误.
故选C.
2.
【答案】
C
【解答】
解:A,同心圆是指圆心相同但半径不同的圆;
B,在同一个圆中优弧一定大于劣弧,但在不同的圆中不一定;
D,这句话成立的条件是在同一圆中.
故选C.
3.
【答案】
D
【解答】
∵ 点P在⊙O上,
∴ 只需要OP⊥EF即可,
4.
【答案】
B
【解答】
解:∵ PA为⊙O的切线,A为切点,PBC是⊙O的割线,
∴ PA2=PB?PC,
∵ PB=BC=2,
∴ PC=4,
∴ PA2=4×2,
∴ PA=22,
故选B.
5.
【答案】
B
【解答】
解:∵ ∠AOB的度数为m,
∴ 弧AB的度数为m,∴ 弧ACB的度数为360?-m,
∴ ∠D+∠E=12(AC+BC)=(360?-m)÷2=180?-m2.
故选B.
6.
【答案】
B
【解答】
解:作直径BD,连接CD,OC,BM,CM,OM,如图所示:
则∠BCD=90?,∠BAC=∠D,
∴ sinD=BCBD=234=32,
∴ ∠BAC=∠D=60?,
∴ ∠BOC=2∠BAC=120?,∠ABC+∠ACB=120?,
∵ P点是△ABC的内心,
∴ ∠PBC+∠PCB=12(∠ABC+∠ACB)=60?,
∴ ∠BPC=120?=∠BOC,
∴ 点O在⊙M上,
∴ OM=CM,
∵ BM=CM,
∴ BM=CM,
∴ ∠BOM=∠COM=60?,
∴ △OCM是等边三角形,
∴ CM=OC=2,
即⊙M的半径不变,等于2.
故选:B.
7.
【答案】
B
【解答】
解:∵ 点C是AB的中点,
∴ OC⊥AB,
∴ ∠AOC=50?,
∴ ∠BOC=50?.故选B.
8.
【答案】
B
【解答】
解:如图,连接OE、OF、OH、OG.
①∵ ⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,
∴ BF=BG、AF=AE,
只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;
故本选项不一定正确;
②根据题意,知,CG、CH都是⊙O的切线,
∴ CG=CH.
故本选项正确;
③根据题意,知
AF=AE,DH=DE,BF=BG,CG=CH,
则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.
故本选项正确;
④当点G是边BC的中点时,BG=CG.
故本选项错误;
综上所述,正确的说法有2个;
故选B.
9.
【答案】
B
【解答】
如图,连接BO,FO,OA.
由题意得,△OAF,△AOB都是等边三角形,
∴ ∠AOF=∠OAB=60?,
∴ AB?//?OF,
∴ △OAB的面积=△ABF的面积,
∵ 六边形ABCDEF是正六边形,
∴ AF=AB,
∴ 图中阴影部分的面积等于扇形OAB的面积×3=60π×22360×3=2π,
10.
【答案】
C
【解答】
解:∵ ∠A与∠BOD是同弧所对的圆周角与圆心角,∠BOD=70?,
∴ ∠A=12∠BOD=35?.
∵ 四边形ABCD是圆内接四边形,
∴ ∠BCD=180?-∠A=180?-35?=145?.
故选C.
二、 填空题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
11.
【答案】
18
【解答】
解:设该圆弧的半径等于rcm,则
5π=50πr180,
解得t=18.
故答案是:18.
12.
【答案】
43
【解答】
解:∵ ∠BAD=30?,∴ ∠C=∠BAD=30?.
∵ CD⊥AB,
∴ ∠CEB=90?,CD=2CE,BC=2BE=4,
∴ CE=BC2-BE2=42-22=23,
∴ CD=2CE=43.
13.
【答案】
85?
【解答】
∵ B是AC的中点,
∴ ∠AOB=2∠BDC=80?,
又∵ M是OD上一点,
∴ ∠AMB≤∠AOB=80?.
则不符合条件的只有85?.
14.
【答案】
6
【解答】
解:设PB=x,则PA=10-x.由相交弦定理得:PA?PB=PC?PD,即x(10-x)=16
解得:x=2或8,
当x=2时,PB=10-2=8,则PB-PA=8-2=6;
当x=6时,PB=10-6=2<6,不合题意舍去.
故应填6.
15.
【答案】
②④
【解答】
解:∵ AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为E,
∴ AB垂直平分CD,
∴ CE=DE,故④正确;
∴ 弧BC=弧BD,故②正确;
∵ AB是⊙O的直径,
∴ AB平分⊙O,
∵ 弧BC=弧BD,
∴ 弧AC=弧AD,故①错误.
∵ CD是⊙O的弦,AB是直径,
∴ AE≠BE,故③错误.
故答案为:②④.
16.
【答案】
6cm
【解答】
解:∵ 点D平分BC,
∴ OD平分BC,
∴ OE为△ABC的中位线,
又∵ ⊙O的直径AB=10cm,
∴ OD=5cm,DE=2cm,
∴ 0E=3cm
则弦AC=6cm.
故答案为6cm.
17.
【答案】
140
【解答】
解:∵ ∠A=110?
∴ ∠C=180?-∠A=70?
∴ ∠BOD=2∠C=140?.
故答案为:140.
18.
【答案】
5
【解答】
因为CD为高,
根据垂径定理:CD平分AB,
又路面AB宽为6米
则有:AD=3?m,
设圆的半径是x米,
在Rt△AOD中,有OA2=AD2+OD2,
即:x2=32+(9-x)2,
解得:x=5,
所以圆的半径长是?5米.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
证明:∵ CD是△ABC的中线,AB=2CD,
∴ AD=BD=CD,
∵ ∠B=60?,
∴ △CDB是等边三角形,
∴ ∠BDC=∠DCB=60?,
∴ ∠A=∠ACD=30?,
∴ ∠ACB=90?,
∴ AB是△ABC的外接圆的直径,
∵ ∠A=30?,∠ACB=90?,
∴ BC=12AB,
∴ △ABC的外接圆的半径为CB.
【解答】
证明:∵ CD是△ABC的中线,AB=2CD,
∴ AD=BD=CD,
∵ ∠B=60?,
∴ △CDB是等边三角形,
∴ ∠BDC=∠DCB=60?,
∴ ∠A=∠ACD=30?,
∴ ∠ACB=90?,
∴ AB是△ABC的外接圆的直径,
∵ ∠A=30?,∠ACB=90?,
∴ BC=12AB,
∴ △ABC的外接圆的半径为CB.
20.
【答案】
证明:连结BM,
∵ AB是⊙O的直径,
∴ ∠AMB=∠BMF=90?,
又∵ AB⊥CD于E,
∴ BC=BD,
∴ ∠CMB=∠BMD,
∴ ∠AMD=∠AMB-∠BMD=∠BMF-∠CMB=∠CMF,
即:∠AMD=∠FMC.
【解答】
证明:连结BM,
∵ AB是⊙O的直径,
∴ ∠AMB=∠BMF=90?,
又∵ AB⊥CD于E,
∴ BC=BD,
∴ ∠CMB=∠BMD,
∴ ∠AMD=∠AMB-∠BMD=∠BMF-∠CMB=∠CMF,
即:∠AMD=∠FMC.
21.
【答案】
(1)证明:
∵ CD切⊙O于点C,
∴ ∠OCD=90?,
∵ ∠ACD=120?,
∴ ∠ACO=30?,
∵ AB是⊙O的直径,
∴ OA=OC=OB,
∴ ∠A=30?,
∴ ∠D=30?,
∴ CA=CD,
(2)∠A=30?,
∴ ∠COB=60?,
∵ CO=BO,
∴ △BOC是等边三角形,
∴ OB=BC,
∵ ∠D=30?,
∴ ∠BCD=∠D=30?,
∴ BD=BC,
∴ BD=OB.
【解答】
(1)证明:
∵ CD切⊙O于点C,
∴ ∠OCD=90?,
∵ ∠ACD=120?,
∴ ∠ACO=30?,
∵ AB是⊙O的直径,
∴ OA=OC=OB,
∴ ∠A=30?,
∴ ∠D=30?,
∴ CA=CD,
(2)∠A=30?,
∴ ∠COB=60?,
∵ CO=BO,
∴ △BOC是等边三角形,
∴ OB=BC,
∵ ∠D=30?,
∴ ∠BCD=∠D=30?,
∴ BD=BC,
∴ BD=OB.
22.
【答案】
证明:∵ A、B分别为CD,EF的中点,
∴ AD=12CD,BE=12EF,
∵ AM=BN,
∴ AD=BE,
∴ CD=EF,
∴ CD=EF.
【解答】
证明:∵ A、B分别为CD,EF的中点,
∴ AD=12CD,BE=12EF,
∵ AM=BN,
∴ AD=BE,
∴ CD=EF,
∴ CD=EF.
23.
【答案】
DE与⊙O相切,
证明:连接OE、OD,
∵ AC是⊙O的切线,
∴ ∠BAC=90?,
∵ OA=OB,AE=EC,
∴ OE?//?BC,
∴ ∠AOE=∠B,∠EOD=∠ODB,
∵ OA=OB,
∴ ∠B=∠ODB,
∴ ∠AOE=∠EOD,
在△AOE和△DOE中,
OA=OD∠AOE=∠DOEOE=OE,
∴ △AOE?△DOE,
∴ ∠ODE=∠BAC=90?,
∴ DE与⊙O相切.
【解答】
此题暂无解答
24.
【答案】
连接OT
∵ OT=OA,
∴ ∠ATO=∠OAT
又∠TAC=∠BAT,
∴ ∠ATO=∠TAC
∴ OT?//?AC
∵ AC⊥PQ,∴ OT⊥PQ,
∴ PQ是⊙O的切线.
过点O作OM⊥AC于M,
则?AM=MD,
又∠OTC=∠ACT=∠OMC=90?,
∴ 四边形OTCM为矩形,
∴ OM=TC=3
在Rt△AOM中,
AM=OA2-OM2=1,
∴ 弦AD的长为2
【解答】
连接OT
∵ OT=OA,
∴ ∠ATO=∠OAT
又∠TAC=∠BAT,
∴ ∠ATO=∠TAC
∴ OT?//?AC
∵ AC⊥PQ,∴ OT⊥PQ,
∴ PQ是⊙O的切线.
过点O作OM⊥AC于M,
则?AM=MD,
又∠OTC=∠ACT=∠OMC=90?,
∴ 四边形OTCM为矩形,
∴ OM=TC=3
在Rt△AOM中,
AM=OA2-OM2=1,
∴ 弦AD的长为2
25.
【答案】
(1)证明见解析;
(2)证明见解析;
(3)CP=16.9cm
【解答】
(1)如图,连接OD,
:BC是○○的直径,
________BAC=90?
AD平分么BAC,
∴ ________BAC=2∠BAD,
BOD=2BAD,
.2BOD=∠BAC=90?
DPIIBC,
.________ODP=∠BOD=90?
….PDLOD,
:OD是○○半径,
…PD是○O的切线;
(2):PDIIBC,
∴ ________ACB=2P
ACB=∠ADB
∴ .ADB=2P
________AB+∠ACD=180? ∴ ACD+∠DCP=180?
________DCP=∠ABD
∴ ΔABD?△DCP;
(3):BC是○○的直径,
∠BDC=∠BAC=90?
在Rt△ABC中,BC=AB2+AC2=13cm
:AD平分么BAC,
∴ 2EAD=∠CAD
∴ 2BOD=∠COD
∴ BD=CE).
在Rt△BCD中,BD2+CD2=BC2
∴ BD=CD=22BC=1322
ΔABD-△DCP
∵ ABCD=BDCP
