北师大版九年级下册数学 2.4二次函数的应用 同步练习(Word版含解析)
文档属性
| 名称 | 北师大版九年级下册数学 2.4二次函数的应用 同步练习(Word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
2.4二次函数的应用
同步练习
一.选择题
1.用一根长60cm的铁丝围成一个矩形,则矩形的最大面积为( )
A.125cm2
B.225cm2
C.200cm2
D.250cm2
2.如图,一位运动员推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=x2+x+,则此运动员把铅球推出多远( )
A.12m
B.10m
C.3m
D.4m
3.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是( )
A.y=﹣x2+50x
B.y=﹣x2+24x
C.y=﹣x2+25x
D.y=﹣x2+26x
4.如图1所示的是山西大同北都桥的照片,桥上面的部分是以抛物线为模型设计而成的,从正面观察该桥的上面部分是一条抛物线,如图2,若AB=60,OC=15,以AB所在直线为x轴,抛物线的顶点C在y轴上建立平面直角坐标系,则此桥上半部分所在抛物线的解析式为( )
A.y=﹣+15
B.y=﹣﹣15
C.y=﹣+15
D.y=﹣﹣15
5.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第17秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒
B.第10秒
C.第12秒
D.第15秒
6.从地面竖直向上先后抛出两个小球,小球的高度h(米)与运动时间t(秒)之间的函数关系式为h=﹣(t﹣3)2+40,若后抛出的小球经过2.5秒比先抛出的小球高米,则抛出两个小球的间隔时间是( )
A.1秒
B.1.5秒
C.2秒
D.2.5秒
7.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
8.学校组织学生去南京进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣.洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
A.12
B.12
C.6
D.6
9.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825
B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900
D.y=﹣2(x﹣65)2+2000
10.一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s
0
1
2
3
4
滑行距离y1/s
0
4.5
14
28.5
48
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270
B.280
C.375
D.450
二.填空题
11.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是s=75t﹣1.5t2,则飞机着陆后从开始滑行到完全停止所用的时间是
秒.
12.一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,则这名男生抛实心球的成绩是
m.
13.如图是一座截面图为抛物线的拱形桥,当拱顶离水面2米高时,水面l为4米,则当水面下降2米时,水面宽度增加
米.
14.学习过二次函数以后,李华同学以y=2x2+6的图象为灵感,为合肥大圩葡萄节设计了一款葡萄酒杯,如图为杯子的设计稿,若AB=4,DE=2,则杯子的高CE长为
.
15.某城市规划修建一座观光人行桥,此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正视图如图所示,已知桥面上三组拱桥都为抛物线的一部分,拱高(抛物线最高点到桥面AB的距离)都为16米,三条抛物线依次与桥面AB相交于点A,C,D,B.则桥长AB=
米.
三.解答题
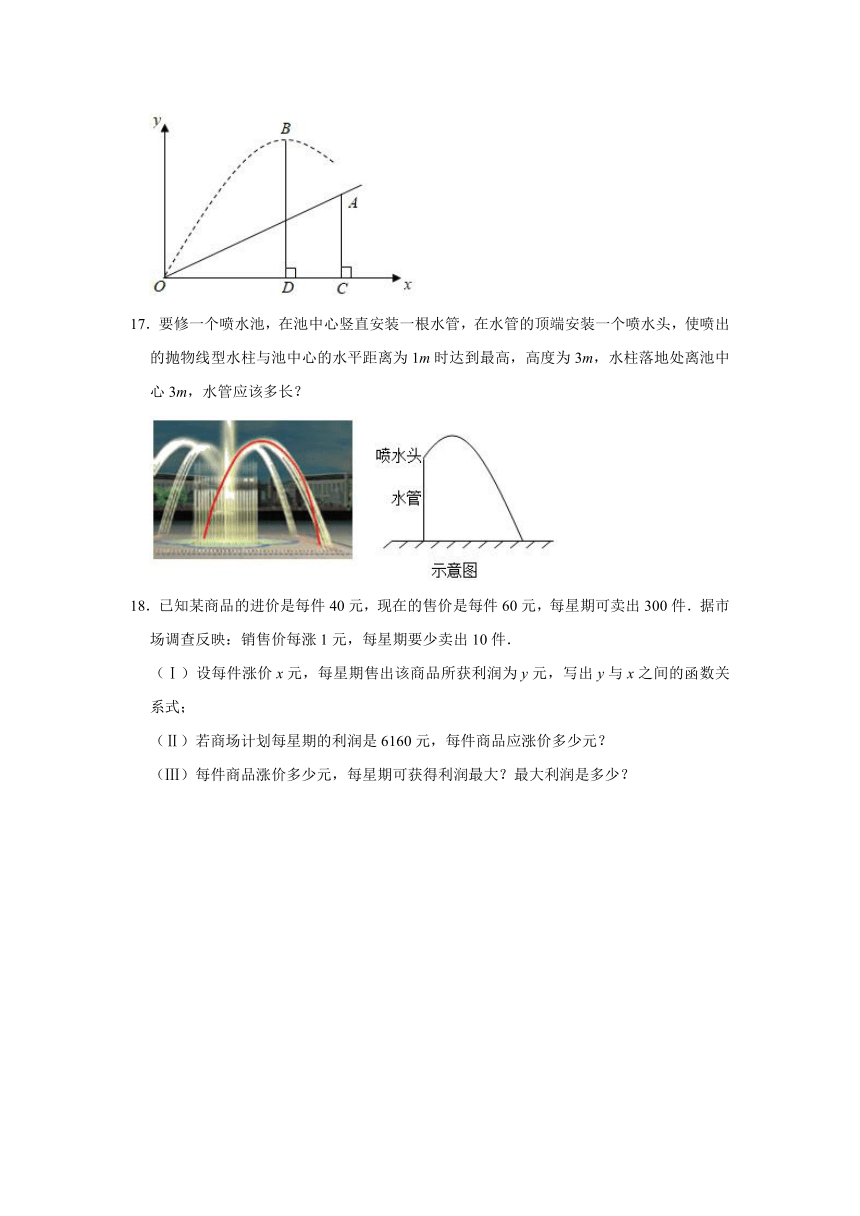
16.如图,小明在一次高尔夫球争霸赛中,从山坡下O点打出一球向球洞A点飞去,球的路线为抛物线,如果不考虑空气阻力,当球移动的水平距离为9米时,球达到最大高度12米.已知山坡OA与水平方向OC的夹角为30o,O、A两点相距米.
(1)求出球的飞行路线所在抛物线的解析式;
(2)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点,并说明理由.
17.要修一个喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线型水柱与池中心的水平距离为1m时达到最高,高度为3m,水柱落地处离池中心3m,水管应该多长?
18.已知某商品的进价是每件40元,现在的售价是每件60元,每星期可卖出300件.据市场调查反映:销售价每涨1元,每星期要少卖出10件.
(Ⅰ)设每件涨价x元,每星期售出该商品所获利润为y元,写出y与x之间的函数关系式;
(Ⅱ)若商场计划每星期的利润是6160元,每件商品应涨价多少元?
(Ⅲ)每件商品涨价多少元,每星期可获得利润最大?最大利润是多少?
参考答案
一.选择题
1.解:设矩形的长为xcm,则宽为,
∴矩形的面积=﹣x2+30x,
∵a=﹣1<0,
∴=(cm2),
故矩形的最大面积是225cm2,
故选:B.
2.解:由题意得:当y=0时,0=x2+x+,
∴x2﹣8x﹣20=0,
∴(x+2)(x﹣10)=0,
∴x1=﹣2(不合题意,舍去),x2=10.
∴此运动员把铅球推出10m.
故选:B.
3.解:设饲养室长为xm,占地面积为ym2,
则y关于x的函数表达式是:y=x?(50+2﹣x)=﹣x2+26x.
故选:D.
4.解:由题意可得:A(﹣30,0),C(0,15),
设二次函数解析式为:y=ax2+c,
则,
解得:a=﹣,
故此桥上半部分所在抛物线的解析式为:y=﹣+15.
故选:A.
5.解:∵此炮弹在第6秒与第17秒时的高度相等,
∴抛物线的对称轴是:x==11.5,
∴炮弹所在高度最高时:
时间是第12秒.
故选:C.
6.解:2.5秒时,后球的高度为:
h2=﹣(2.5﹣3)2+40=,
则此时,前球的高度为h1=﹣=,
令﹣(t﹣3)2+40=,整理得(t﹣3)2=1,
∴t1=4,t2=2(舍),
△t=4﹣2.5=1.5.
故选:B.
7.解:根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即﹣==6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=﹣x2+2x+4
=﹣(x﹣6)2+10
当y=8时,
8=﹣(x﹣6)2+10,
解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.
所以两排灯的水平距离最小是4.
故选:D.
8.解:根据题意:
GH所在直线为x轴,GH的垂直平分线所在直线为y轴建立如图所示的平面直角坐标系,
喷口B为抛物线顶点,共线的三点B、D、H所在直线为抛物线的对称轴,
根据题意,Q(9,15.5),B(6,16),OH=6,
设抛物线解析式为y=﹣a(x﹣6)2+16,
将点Q代入解得a=﹣,
符号题意:洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣.
所以抛物线解析式为:
y=﹣(x﹣6)2+16
=﹣x2+x+14.
当y=0时,即0=﹣x2+x+14,
解得:x=6+12(负值舍去),
所以洗手液落在台面的位置距DH的水平距离是12cm.
故选:B.
9.解:设二次函数的解析式为:y=ax2+bx+c,
∵当x=55,75,80时,y=1800,1800,1550,
∴,
解得,
∴y与x的函数关系式是y=﹣2x2+260x﹣6450=﹣2(x﹣65)2+2000,
故选:D.
10.解:设y1=a+bt1,
把(1,4.5)和(2,14)代入函数解析式得,
,
解得:,
∴二次函数解析式为:y1=2.5t12+2t1…①;
y2=52t﹣2t2,函数在对称轴上取得最大值,即滑雪者停下,
此时,t=﹣=13,
则:滑雪者在AB段用的时间为23﹣13=10,
把t=10代入①式,
解得:则AB=y1=270(米),
故选:A.
二.填空题
11.解:由题意得,
s=75t﹣1.5t2
=﹣1.5(t2﹣50t+625﹣625)
=﹣1.5(t﹣25)2+937.5,
即当t=25秒时,飞机才能停下来.
故答案是:25.
12.解:∵一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,
∴当y=0,则0=﹣x2+x+,
解得:x1=10,x2=﹣2,
∴这名男生抛实心球的成绩为10m,
故答案为:10.
13.解:建立平面直角坐标系如图所示:
则抛物线顶点C的坐标为(0,2),
设抛物线的解析式为y=ax2+2,
将A点坐标(﹣2,0)代入,可得:0=4a+2,
解得:a=﹣,
故抛物线的解析式为y=﹣x2+2,
当水面下降2米,即当y=﹣2时,求对应的抛物线上两点之间的距离,
也就是直线y=﹣2与抛物线相交的两点之间的距离,
将y=﹣2代入抛物线解析式得出:﹣2=﹣x2+2,
解得:x=±2,
所以水面宽度为4米,
故水面宽度增加了(4﹣4)米,
故答案为:4﹣4.
14.解:建立如图所示的平面直角坐标系,
由题意可得:D点坐标为:(0,6),
∵AB=4,
∴B点的横坐标为:2,
故x=2时,y=2×4+6=14,
即B(2,14),
则DC=14﹣6=8,
故CE=DC+DE=8+2=10,
故答案为:10.
15.解:如图,以线段AC的中垂线为y轴,AB为x轴,建立平面直角坐标系,
则抛物线AC的顶点坐标为(0,16),
所以抛物线解析式为y=﹣x2+16,
当y=0时,x1=16,x2=﹣16,
∴点A的坐标为(﹣16,0),点C的坐标为(16,0),
∴AC=16﹣(﹣16)=16+16=32,
∴AB=3AC=96,
即桥长AB为96米;
故答案为:96.
三.解答题
16.解:(1)∵顶点B的坐标是(9,12),
∴设抛物线的解析式为y=a(x﹣9)2+12,
∵点O的坐标是(0,0)
∴把点O的坐标代入得:0=a(0﹣9)2+12,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣9)2+12
即y=﹣x2+x;
(2)在Rt△AOC中,
∵∠AOC=30°,OA=8,
∴AC=OA?sin30°=8×=4,
OC=OA?cos30°=8×=12.
∴点A的坐标为(12,4),
∵当x=12时,y=≠4,
∴小明这一杆不能把高尔夫球从O点直接打入球洞A点.
17.解:建立如图所示平面直角坐标系,
设抛物线解析式为y=a(x﹣h)2+k,
由题意,顶点坐标为(1,3),
∴y=a(x﹣1)2+3,
∵抛物线经过点(3,0),
∴0=a(3﹣1)2+3,
解得a=﹣,
∴y=﹣(x﹣1)2+3,
当x=0时,,
∴水柱落地处离池中心3m时,水管长为m.
18.解:(Ⅰ)销售价每涨1元,每星期要少卖出10件,
∴每星期实际可卖出(300﹣10x)件,
y=(60﹣40+x)(300﹣10x)
=﹣10x2+100x+6000;
(Ⅱ)根据题意,得:﹣10x2+100x+6000=6160,
整理,得:x2﹣10x+16=0,
解得x1=2,x2=8,
答:若商场计划每星期的利润是6160元,每件商品应涨价2元或8元;
(Ⅲ)y=﹣10x2+100x+6000=﹣10(x﹣5)2+6250,
∵a=﹣10<0,
∴当x=5时,y取得最大值6250,
答:每件商品涨价5元,每星期可获得利润最大,最大利润是6250元.
同步练习
一.选择题
1.用一根长60cm的铁丝围成一个矩形,则矩形的最大面积为( )
A.125cm2
B.225cm2
C.200cm2
D.250cm2
2.如图,一位运动员推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=x2+x+,则此运动员把铅球推出多远( )
A.12m
B.10m
C.3m
D.4m
3.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是( )
A.y=﹣x2+50x
B.y=﹣x2+24x
C.y=﹣x2+25x
D.y=﹣x2+26x
4.如图1所示的是山西大同北都桥的照片,桥上面的部分是以抛物线为模型设计而成的,从正面观察该桥的上面部分是一条抛物线,如图2,若AB=60,OC=15,以AB所在直线为x轴,抛物线的顶点C在y轴上建立平面直角坐标系,则此桥上半部分所在抛物线的解析式为( )
A.y=﹣+15
B.y=﹣﹣15
C.y=﹣+15
D.y=﹣﹣15
5.向空中发射一枚炮弹,第x秒时的高度为y米,且高度与时间的关系为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第17秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒
B.第10秒
C.第12秒
D.第15秒
6.从地面竖直向上先后抛出两个小球,小球的高度h(米)与运动时间t(秒)之间的函数关系式为h=﹣(t﹣3)2+40,若后抛出的小球经过2.5秒比先抛出的小球高米,则抛出两个小球的间隔时间是( )
A.1秒
B.1.5秒
C.2秒
D.2.5秒
7.如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣x2+bx+c表示.在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2m
B.4m
C.4
m
D.4m
8.学校组织学生去南京进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣.洗手液瓶子的截面图下部分是矩形CGHD.小王同学测得:洗手液瓶子的底面直径GH=12cm,喷嘴位置点B距台面的距离为16cm,且B、D、H三点共线.小王在距离台面15.5cm处接洗手液时,手心Q到直线DH的水平距离为3cm,若小王不去接,则洗手液落在台面的位置距DH的水平距离是( )cm.
A.12
B.12
C.6
D.6
9.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825
B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900
D.y=﹣2(x﹣65)2+2000
10.一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s
0
1
2
3
4
滑行距离y1/s
0
4.5
14
28.5
48
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270
B.280
C.375
D.450
二.填空题
11.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是s=75t﹣1.5t2,则飞机着陆后从开始滑行到完全停止所用的时间是
秒.
12.一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,则这名男生抛实心球的成绩是
m.
13.如图是一座截面图为抛物线的拱形桥,当拱顶离水面2米高时,水面l为4米,则当水面下降2米时,水面宽度增加
米.
14.学习过二次函数以后,李华同学以y=2x2+6的图象为灵感,为合肥大圩葡萄节设计了一款葡萄酒杯,如图为杯子的设计稿,若AB=4,DE=2,则杯子的高CE长为
.
15.某城市规划修建一座观光人行桥,此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正视图如图所示,已知桥面上三组拱桥都为抛物线的一部分,拱高(抛物线最高点到桥面AB的距离)都为16米,三条抛物线依次与桥面AB相交于点A,C,D,B.则桥长AB=
米.
三.解答题
16.如图,小明在一次高尔夫球争霸赛中,从山坡下O点打出一球向球洞A点飞去,球的路线为抛物线,如果不考虑空气阻力,当球移动的水平距离为9米时,球达到最大高度12米.已知山坡OA与水平方向OC的夹角为30o,O、A两点相距米.
(1)求出球的飞行路线所在抛物线的解析式;
(2)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点,并说明理由.
17.要修一个喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线型水柱与池中心的水平距离为1m时达到最高,高度为3m,水柱落地处离池中心3m,水管应该多长?
18.已知某商品的进价是每件40元,现在的售价是每件60元,每星期可卖出300件.据市场调查反映:销售价每涨1元,每星期要少卖出10件.
(Ⅰ)设每件涨价x元,每星期售出该商品所获利润为y元,写出y与x之间的函数关系式;
(Ⅱ)若商场计划每星期的利润是6160元,每件商品应涨价多少元?
(Ⅲ)每件商品涨价多少元,每星期可获得利润最大?最大利润是多少?
参考答案
一.选择题
1.解:设矩形的长为xcm,则宽为,
∴矩形的面积=﹣x2+30x,
∵a=﹣1<0,
∴=(cm2),
故矩形的最大面积是225cm2,
故选:B.
2.解:由题意得:当y=0时,0=x2+x+,
∴x2﹣8x﹣20=0,
∴(x+2)(x﹣10)=0,
∴x1=﹣2(不合题意,舍去),x2=10.
∴此运动员把铅球推出10m.
故选:B.
3.解:设饲养室长为xm,占地面积为ym2,
则y关于x的函数表达式是:y=x?(50+2﹣x)=﹣x2+26x.
故选:D.
4.解:由题意可得:A(﹣30,0),C(0,15),
设二次函数解析式为:y=ax2+c,
则,
解得:a=﹣,
故此桥上半部分所在抛物线的解析式为:y=﹣+15.
故选:A.
5.解:∵此炮弹在第6秒与第17秒时的高度相等,
∴抛物线的对称轴是:x==11.5,
∴炮弹所在高度最高时:
时间是第12秒.
故选:C.
6.解:2.5秒时,后球的高度为:
h2=﹣(2.5﹣3)2+40=,
则此时,前球的高度为h1=﹣=,
令﹣(t﹣3)2+40=,整理得(t﹣3)2=1,
∴t1=4,t2=2(舍),
△t=4﹣2.5=1.5.
故选:B.
7.解:根据题意,得
OA=12,OC=4.
所以抛物线的顶点横坐标为6,
即﹣==6,
∴b=2,
∵C(0,4),
∴c=4,
所以抛物线解析式为:
y=﹣x2+2x+4
=﹣(x﹣6)2+10
当y=8时,
8=﹣(x﹣6)2+10,
解得x1=6+2,x2=6﹣2.
则x1﹣x2=4.
所以两排灯的水平距离最小是4.
故选:D.
8.解:根据题意:
GH所在直线为x轴,GH的垂直平分线所在直线为y轴建立如图所示的平面直角坐标系,
喷口B为抛物线顶点,共线的三点B、D、H所在直线为抛物线的对称轴,
根据题意,Q(9,15.5),B(6,16),OH=6,
设抛物线解析式为y=﹣a(x﹣6)2+16,
将点Q代入解得a=﹣,
符号题意:洗手液从喷口B流出,路线近似呈抛物线状,且a=﹣.
所以抛物线解析式为:
y=﹣(x﹣6)2+16
=﹣x2+x+14.
当y=0时,即0=﹣x2+x+14,
解得:x=6+12(负值舍去),
所以洗手液落在台面的位置距DH的水平距离是12cm.
故选:B.
9.解:设二次函数的解析式为:y=ax2+bx+c,
∵当x=55,75,80时,y=1800,1800,1550,
∴,
解得,
∴y与x的函数关系式是y=﹣2x2+260x﹣6450=﹣2(x﹣65)2+2000,
故选:D.
10.解:设y1=a+bt1,
把(1,4.5)和(2,14)代入函数解析式得,
,
解得:,
∴二次函数解析式为:y1=2.5t12+2t1…①;
y2=52t﹣2t2,函数在对称轴上取得最大值,即滑雪者停下,
此时,t=﹣=13,
则:滑雪者在AB段用的时间为23﹣13=10,
把t=10代入①式,
解得:则AB=y1=270(米),
故选:A.
二.填空题
11.解:由题意得,
s=75t﹣1.5t2
=﹣1.5(t2﹣50t+625﹣625)
=﹣1.5(t﹣25)2+937.5,
即当t=25秒时,飞机才能停下来.
故答案是:25.
12.解:∵一名男生参加抛实心球测试,已知球的高度y(m)与水平距离x(m)之间的关系是,
∴当y=0,则0=﹣x2+x+,
解得:x1=10,x2=﹣2,
∴这名男生抛实心球的成绩为10m,
故答案为:10.
13.解:建立平面直角坐标系如图所示:
则抛物线顶点C的坐标为(0,2),
设抛物线的解析式为y=ax2+2,
将A点坐标(﹣2,0)代入,可得:0=4a+2,
解得:a=﹣,
故抛物线的解析式为y=﹣x2+2,
当水面下降2米,即当y=﹣2时,求对应的抛物线上两点之间的距离,
也就是直线y=﹣2与抛物线相交的两点之间的距离,
将y=﹣2代入抛物线解析式得出:﹣2=﹣x2+2,
解得:x=±2,
所以水面宽度为4米,
故水面宽度增加了(4﹣4)米,
故答案为:4﹣4.
14.解:建立如图所示的平面直角坐标系,
由题意可得:D点坐标为:(0,6),
∵AB=4,
∴B点的横坐标为:2,
故x=2时,y=2×4+6=14,
即B(2,14),
则DC=14﹣6=8,
故CE=DC+DE=8+2=10,
故答案为:10.
15.解:如图,以线段AC的中垂线为y轴,AB为x轴,建立平面直角坐标系,
则抛物线AC的顶点坐标为(0,16),
所以抛物线解析式为y=﹣x2+16,
当y=0时,x1=16,x2=﹣16,
∴点A的坐标为(﹣16,0),点C的坐标为(16,0),
∴AC=16﹣(﹣16)=16+16=32,
∴AB=3AC=96,
即桥长AB为96米;
故答案为:96.
三.解答题
16.解:(1)∵顶点B的坐标是(9,12),
∴设抛物线的解析式为y=a(x﹣9)2+12,
∵点O的坐标是(0,0)
∴把点O的坐标代入得:0=a(0﹣9)2+12,
解得a=﹣,
∴抛物线的解析式为y=﹣(x﹣9)2+12
即y=﹣x2+x;
(2)在Rt△AOC中,
∵∠AOC=30°,OA=8,
∴AC=OA?sin30°=8×=4,
OC=OA?cos30°=8×=12.
∴点A的坐标为(12,4),
∵当x=12时,y=≠4,
∴小明这一杆不能把高尔夫球从O点直接打入球洞A点.
17.解:建立如图所示平面直角坐标系,
设抛物线解析式为y=a(x﹣h)2+k,
由题意,顶点坐标为(1,3),
∴y=a(x﹣1)2+3,
∵抛物线经过点(3,0),
∴0=a(3﹣1)2+3,
解得a=﹣,
∴y=﹣(x﹣1)2+3,
当x=0时,,
∴水柱落地处离池中心3m时,水管长为m.
18.解:(Ⅰ)销售价每涨1元,每星期要少卖出10件,
∴每星期实际可卖出(300﹣10x)件,
y=(60﹣40+x)(300﹣10x)
=﹣10x2+100x+6000;
(Ⅱ)根据题意,得:﹣10x2+100x+6000=6160,
整理,得:x2﹣10x+16=0,
解得x1=2,x2=8,
答:若商场计划每星期的利润是6160元,每件商品应涨价2元或8元;
(Ⅲ)y=﹣10x2+100x+6000=﹣10(x﹣5)2+6250,
∵a=﹣10<0,
∴当x=5时,y取得最大值6250,
答:每件商品涨价5元,每星期可获得利润最大,最大利润是6250元.
