沪科版九年级数学上册21.2二次函数的图象和性质中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版九年级数学上册21.2二次函数的图象和性质中考题汇编(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览

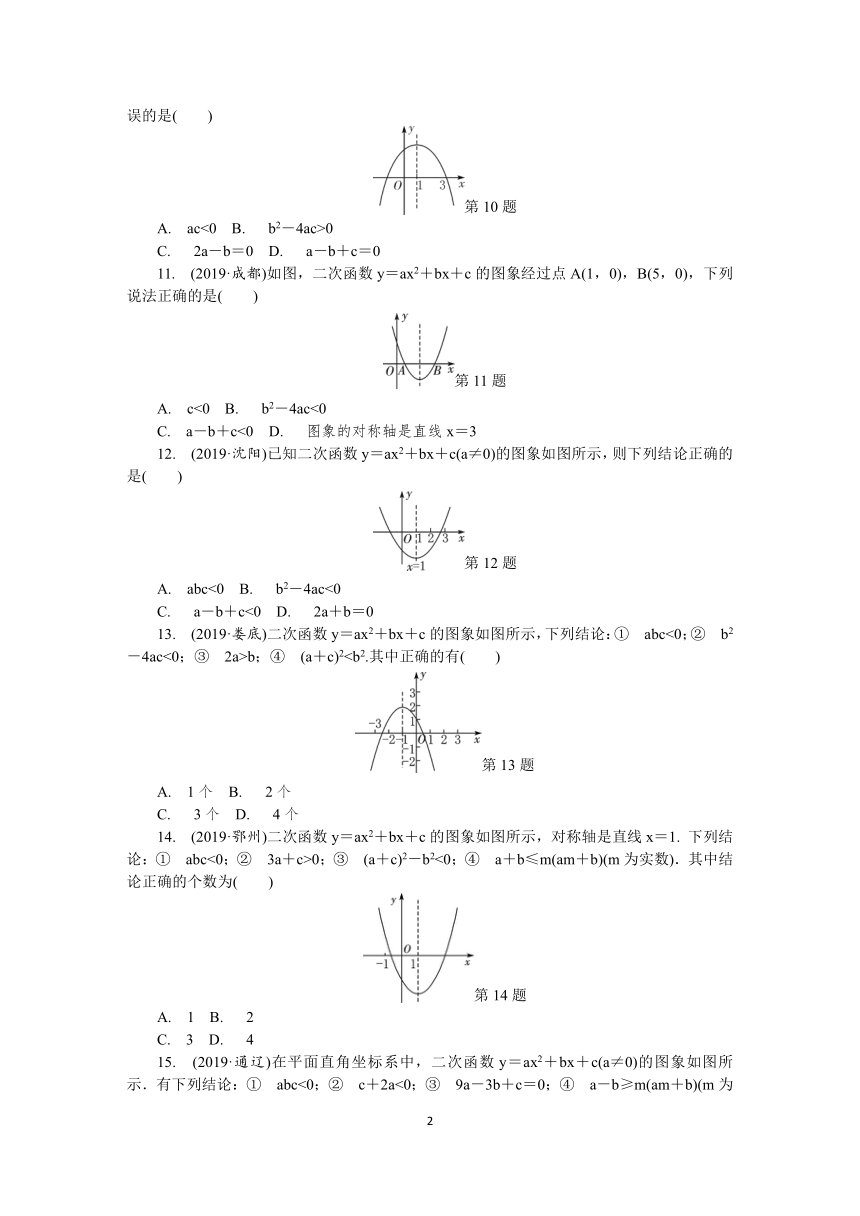
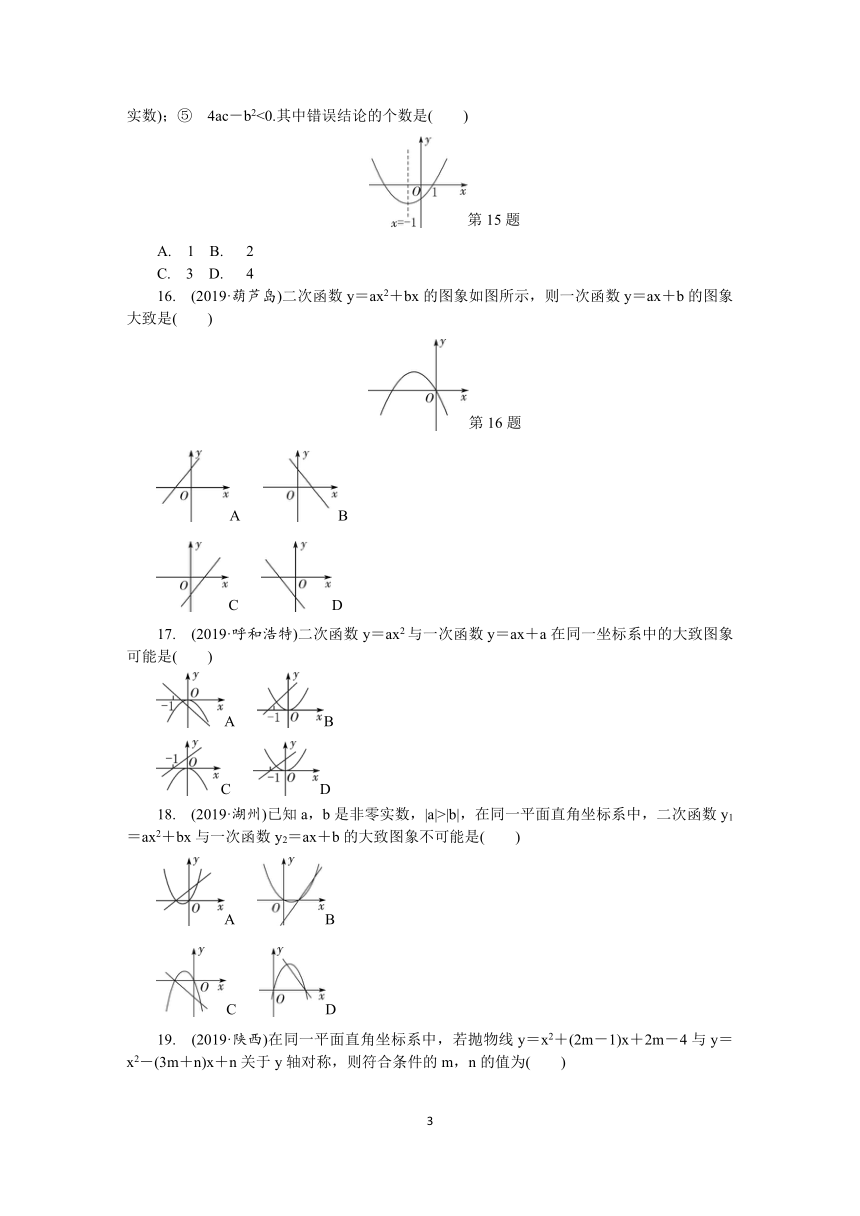


文档简介
沪科版九年级数学上册二次函数的图象和性质中考题汇编(含答案)
10
一、
选择题
1.
(2019·衢州)二次函数y=(x-1)2+3图象的顶点坐标是( )
A.
(1,3)
B.
(1,-3)
C.
(-1,3)
D.
(-1,-3)
2.
(2019·重庆)抛物线y=-3x2+6x+2的对称轴是( )
A.
直线x=2
B.
直线x=-2
C.
直线x=1
D.
直线x=-1
3.
(2019·河南)已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为( )
A.
-2
B.
-4
C.
2
D.
4
4.
(2019·兰州)已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是( )
A.
2>y1>y2
B.
2>y2>y1
C.
y1>y2>2
D.
y2>y1>2
5.
(2019·哈尔滨)将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线对应的函数解析式为( )
A.
y=2(x+2)2+3
B.
y=2(x-2)2+3
C.
y=2(x-2)2-3
D.
y=2(x+2)2-3
6.
(2019·西藏)要得到函数y=-(x-1)2+1的图象,可以把函数y=-x2的图象( )
A.
向左平移1个单位长度,再向下平移1个单位长度
B.
向左平移1个单位长度,再向上平移1个单位长度
C.
向右平移1个单位长度,再向上平移1个单位长度
D.
向右平移1个单位长度,再向下平移1个单位长度
7.
(2019·百色)要得到抛物线y=x2+6x+7,可把抛物线y=x2( )
A.
先向左平移3个单位长度,再向下平移2个单位长度
B.
先向左平移6个单位长度,再向上平移7个单位长度
C.
先向左平移3个单位长度,再向上平移2个单位长度
D.
先回右平移3个单位长度,再向上平移2个单位长度
8.
(2019·雅安)在平面直角坐标系中,对于二次函数y=(x-2)2+1,下列说法错误的是( )
A.
y的最小值为1
B.
图象顶点坐标为(2,1),对称轴为直线x=2
C.
当x<2时,y的值随x值的增大而增大,当x≥2时,y的值随x值的增大而减小
D.
它的图象可以由y=x2的图象先向右平移2个单位长度,再向上平移1个单位长度得到
9.
(2019·淄博)将二次函数y=x2-4x+a的图象向左平移1个单位长度,再向上平移1个单位长度,若得到的函数图象与直线y=2有两个交点,则a的取值范围是( )
A.
a>3
B.
a<3
C.
a>5
D.
a<5
10.
(2019·河池)如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是( )
A.
ac<0
B.
b2-4ac>0
C.
2a-b=0
D.
a-b+c=0
11.
(2019·成都)如图,二次函数y=ax2+bx+c的图象经过点A(1,0),B(5,0),下列说法正确的是( )
A.
c<0
B.
b2-4ac<0
C.
a-b+c<0
D.
图象的对称轴是直线x=3
12.
(2019·沈阳)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A.
abc<0
B.
b2-4ac<0
C.
a-b+c<0
D.
2a+b=0
13.
(2019·娄底)二次函数y=ax2+bx+c的图象如图所示,下列结论:①
abc<0;②
b2-4ac<0;③
2a>b;④
(a+c)2A.
1个
B.
2个
C.
3个
D.
4个
14.
(2019·鄂州)二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.
下列结论:①
abc<0;②
3a+c>0;③
(a+c)2-b2<0;④
a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
A.
1
B.
2
C.
3
D.
4
15.
(2019·通辽)在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①
abc<0;②
c+2a<0;③
9a-3b+c=0;④
a-b≥m(am+b)(m为实数);⑤
4ac-b2<0.其中错误结论的个数是( )
A.
1
B.
2
C.
3
D.
4
16.
(2019·葫芦岛)二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象大致是( )
17.
(2019·呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
18.
(2019·湖州)已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )
19.
(2019·陕西)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m,n的值为( )
A.
,-
B.
5,-6
C.
-1,6
D.
1,-2
20.
(2019·贵阳)如图,在平面直角坐标系中,已知点A(-1,0),点B(1,1)都在直线y=x+上,若抛物线y=ax2-x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( )
A.
a≤-2
B.
a<
C.
1≤a<或a≤-2
D.
-2≤a<
21.
(2019·玉林)如图,抛物线C:y=(x-1)2-1,顶点为D,将C沿水平方向向右(或向左)平移m个单位长度,得到抛物线C1,顶点为D1,C与C1相交于点Q,若∠DQD1=60°,则m的值为( )
A.
±4
B.
±2
C.
-2或2
D.
-4或4
22.
(2019·宜宾)已知抛物线y=x2-1与y轴交于点A,与直线y=kx(k为任意实数)相交于B,C两点,则下列结论不正确的是( )
A.
存在实数k,使得△ABC为等腰三角形
B.
存在实数k,使得△ABC的内角中有两角分别为30°和60°
C.
任意实数k,使得△ABC都为直角三角形
D.
存在实数k,使得△ABC为等边三角形
23.
(2019·福建)若二次函数y=|a|x2+bx+c的图象经过不同的五点A(m,n),B(0,y1),C(3-m,n),D(,y2),E(2,y3),则y1,y2,y3的大小关系是( )
A.
y1B.
y1C.
y3D.
y224.
(2019·资阳)如图是函数y=x2-2x-3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A.
m≥1
B.
m≤0
C.
0≤m≤1
D.
m≥1或m≤0
25.
(2019·岳阳)对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1,x2,且x1<1A.
c<-3
B.
c<-2
C.
c<
D.
c<1
二、
填空题
26.
(2019·哈尔滨)二次函数y=-(x-6)2+8的最大值是________.
27.
(2019·荆州)二次函数y=-2x2-4x+5的最大值是________.
28.
(2019·白银)将二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为____________.
29.
(2019·凉山州)将抛物线y=(x-3)2-2向左平移________个单位长度后经过点A(2,2).
30.
(2019·宜宾)将抛物线y=2x2的图象,向左平移1个单位长度,再向下平移2个单位长度,所得图象对应的函数解析式为______________.
31.
(2019·广元)如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是__________.
32.
(2019·天水)二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b,N=a-b.则M,N的大小关系为M________N(填“>”“<”或“=”).
33.
(2019·荆门)抛物线y=ax2+bx+c(a,b,c为常数)的顶点为P,且抛物线经过点A(-1,0),B(m,0),C(-2,n)(1abc>0;②
3a+c<0;③
a(m-1)+2b>0;④
当a=-1时,存在点P使△PAB为直角三角形.其中正确的为________(填序号).
34.
(2019·镇江)已知抛物线y=ax2+4ax+4a+1(a≠0)过点A(m,3),B(n,3)两点,若线段AB的长不大于4,则代数式a2+a+1的最小值是________.
35.
(2019·内江)若x,y,z为实数,且则代数式x2-3y2+z2的最大值是________.
36.
(2019·雅安)函数y=的图象如图所示.若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为__________.
37.
(2019·大庆)如图,抛物线y=x2(p>0),点F(0,p),直线l:y=-p,已知抛物线上的点到点F的距离与到直线l的距离相等,过点F的直线与抛物线交于A,B两点,AA1⊥l,BB1⊥l,垂足分别为A1,B1,连接A1F,B1F,A1O,B1O.若A1F=a,B1F=b,则△A1OB1的面积为________(只用a,b表示).
38.
(2019·衡阳)在平面直角坐标系中,抛物线y=x2的图象如图所示.已知点A的坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4,…,依次进行下去,则点A2
019的坐标为____________.
三、
解答题
39.
(2019·宁波)如图,二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)
求a的值和图象的顶点坐标.
(2)
点Q(m,n)在该二次函数图象上.
①
当m=2时,求n的值;
②
若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
第39题
40.(2019·永州)如图,抛物线经过两点A(-3,0),B(0,3),且其对称轴为直线x=-1.
(1)
求此抛物线对应的函数解析式;
(2)
若P是抛物线上点A与点B之间的动点(不包括点A,B),求△PAB面积的最大值,并求出此时点P的坐标.
第40题
41.
(2019·安徽)一次函数y=kx+4与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)
求k,a,c的值;
(2)
过点A(0,m)(042.(2019·台州)已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4).
(1)
求b,c满足的关系式;
(2)
设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;
(3)
若该函数的图象不经过第三象限,当-5≤x≤1时,函数的最大值与最小值之差为16,求b的值.
43.(2019·南通)已知二次函数y=x2-4x+3a+2(a为常数).
(1)
请写出该二次函数的三条性质;
(2)
在同一直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,求a的取值范围.
44.(2019·北京)在平面直角坐标系xOy中,抛物线y=ax2+bx-与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)
求点B的坐标(用含a的式子表示);
(2)
求抛物线的对称轴;
(3)
已知点P,Q(2,2).若抛物线与线段PQ恰有一个公共点,结合图象,求a的取值范围.
45.(2019·天门)在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)
若抛物线C与直线l有交点,求a的取值范围;
(2)
当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
(3)
若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
46.(2019·上海)如图,在平面直角坐标系xOy中,抛物线y=x2-2x,其顶点为A.
(1)
写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)
我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.
①
试求抛物线y=x2-2x的“不动点”的坐标;
②
平移抛物线y=x2-2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC是梯形,求新抛物线对应的函数解析式.
第46题
47.(2019·河北)如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x-b与y轴交于点B;抛物线L:y=-x2+bx的顶点为C,且L与x轴的右交点为D.
(1)
若AB=8,求b的值,并求此时抛物线L的对称轴与直线a的交点坐标;
(2)
当点C在l下方时,求点C与l距离的最大值;
(3)
设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)
在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2
019和b=2
019.5时“美点”的个数.
第47题
参考答案
一、
A
C
B
A
B
C
A
C
D
C
D
D
A
C
A
D
D
D
D
C
A
D
D
C
B
二、
8
7
y=(x-2)2+1
3
y=2(x+1)2-2
-6<
②③
26
0
(-1
010,1
0102)
三、
(1)
把点P(-2,3)代入y=x2+ax+3中,得3=4-2a+3,解得a=2.∴
二次函数的解析式为y=x2+2x+3=(x+1)2+2.∴
顶点坐标为(-1,2) (2)
①
当m=2时,n=(2+1)2+2=11 ②
∵
点Q到y轴的距离小于2,∴
|m|<2.∴
-2结合图象可知,n的取值范围为2≤n<11
(1)
∵
抛物线的对称轴是直线x=-1,且经过点A(-3,0),∴
由抛物线的对称性可知,抛物线还经过点(1,0).设抛物线对应的函数解析式为y=a(x-1)(x+3),把B(0,3)代入,得3=-3a,解得a=-1.∴
抛物线对应的函数解析式为y=-x2-2x+3 (2)
设直线AB对应的函数解析式为y=kx+b,∵
点A(-3,0),B(0,3)在直线y=kx+b上,∴
解得∴
直线AB对应的函数解析式为y=x+3.过点P作PQ⊥x轴于点Q,交直线AB于点M,设P(x,-x2-2x+3),则M(x,x+3),∴
PM=-x2-2x+3-(x+3)=-x2-3x.∴
S△PAB=(-x2-3x)×3=-(x+)2+.当x=-时,S△PAB有最大值,为,此时点P的纵坐标为--2×+3=,∴
△PAB面积的最大值为,此时点P的坐标为
(1)
根据题意,得二次函数y=ax2+c的图象的顶点坐标为(0,c).将点(0,c),(1,2)代入一次函数的解析式,得解得将点(1,2)代入y=ax2+4,得2=a+4,解得a=-2.∴
k的值为-2,a的值为-2,c的值为4 (2)
由(1)可知,二次函数的解析式为y=-2x2+4.令y=m,得2x2+m-4=0,解得x=±.设B,C两点的坐标分别为(x1,m),(x2,m),则BC=|x1-x2|=2.∴
W=OA2+BC2=m2+4×=m2-2m+8=(m-1)2+7.∵
0当m=1时,W有最小值,为7
(1)
将点(-2,4)代入y=x2+bx+c,得4=4-2b+c,即-2b+c=0,∴
c=2b (2)
根据题意,得m=-,n=.∴
b=-2m.又由(1)知,c=2b,∴
c=-4m.∴
n===-m2-4m (3)
如图,由(2)的结论,画出函数y=x2+bx+c和函数y=-x2-4x的图象.∵
函数y=x2+bx+c的图象不经过第三象限,∴
-4≤-≤0.①
当-4≤-≤-2,即4≤b≤8时,如图①.当x=1时,函数取到最大值,为1+3b;当x=-时,函数取到最小值,为.∴
1+3b-=16,即b2+4b-60=0,解得b1=6,b2=-10(不合题意,舍去).②
当-2<-≤0,即0≤b<4时,如图②.当x=-5时,函数取到最大值,为25-3b;当x=-时,函数取到最小值,为,∴
25-3b-=16,即b2-20b+36=0,解得b1=2,b2=18(不合题意,舍去).综上所述,b的值为2或6
(1)
答案不唯一,如①
图象开口向上;②
图象的对称轴为直线x=2;③
当x>2时,y随x的增大而增大 (2)
∵
二次函数的图象与一次函数y=2x-1的图象有两个交点,∴
x2-4x+3a+2=2x-1,即x2-6x+3a+3=0.∴
Δ=36-4(3a+3)=-12a+24>0,解得a<2.∵
二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,∴
二次函数y=x2-6x+3a+3的图象与x轴x≤4的部分有两个交点.结合图象(图略)可知,当x=4时,x2-6x+3a+3≥0.∴
当x=4时,x2-6x+3a+3=3a-5≥0,解得a≥.∴
当二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点时,a的取值范围为≤a<2
(1)
由题意,得A,又∵
将点A向右平移2个单位长度,得到点B,∴
B (2)
∵
点A与点B关于直线x=1对称,点A,B均在抛物线上,∴
抛物线的对称轴为直线x=1 (3)
①
当a>0时,则-<0.结合图象(图略)可知,此时线段PQ与抛物线没有交点.②
当a<0时,则->0.结合图象(图略)可知,此时-≤2,解得a≤-.综上所述,当a≤-时,抛物线与线段PQ恰有一个公共点
(1)
将点A(-3,-3),B(1,-1)代入y=kx+b,得解得∴
直线l对应的函数解析式为y=x-.联立y=ax2+2x-1与y=x-,得2ax2+3x+1=0.∵
抛物线C与直线l有交点,∴
Δ=9-8a≥0,解得a≤.又∵
a≠0,∴
a的取值范围为a≤且a≠0 (2)
根据题意,得二次函数的解析式为y=-x2+2x-1=-(x-1)2.∵
-1<0,∴
二次函数的图象开口向下,对称轴为直线x=1.∵
当m≤x≤m+2时,y有最大值-4,∴
当y=-4时,有-(x-1)2=-4,解得x=-1或x=3.①
当x<1时,y随x的增大而增大,∴
当x=m+2=-1时,y有最大值-4,此时m=-3;②
当x>1时,y随x的增大而减小,∴
当x=m=3时,y有最大值-4.综上所述,m的值为-3或3 (3)
≤a<或a≤-2
(1)
对于抛物线y=x2-2x=(x-1)2-1,其开口向上,顶点A的坐标为(1,-1);当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小 (2)
①
设抛物线“不动点”坐标为(t,t),则t=t2-2t.解得t=0或3.∴
“不动点”的坐标为(0,0)或(3,3) ②
∵
新抛物线顶点B为“不动点”,则设点B(m,m),∴
新抛物线的对称轴为直线x=m,与x轴的交点C的坐标为(m,0).∵
四边形OABC是梯形,∴
直线x=m在y轴左侧.∵
BC与OA不平行,∴
OC∥AB.又∵
点A的坐标为(1,-1),点B的坐标为(m,m),∴
m=-1.∴
新抛物线是由抛物线y=x2-2x向左平移2个单位长度得到的.∴
新抛物线对应的函数表达式为y=(x+1)2-1
(1)
当x=0时,y=x-b=-b,∴
点B的坐标为(0,-b).∵
AB=8,而点A的坐标为(0,b),∴
b-(-b)=8.解得b=4.∴
抛物线L对应的函数解析式为y=-x2+4x.∴
抛物线L的对称轴为直线x=2.当x=2时,y=x-4=-2.∴
抛物线L的对称轴与直线a的交点坐标为(2,-2
) (2)
∵
y=-x2+bx=-+,∴
抛物线L的顶点C的坐标为.∵
点C在l下方,∴
C与l的距离为b-=-(b-2)2+1≤1.∴
点C与l距离的最大值为1 (3)
由题意,得y3=,即y1+y2=2y3,得b+x0-b=2(-x+bx0).解得x0=0或x0=b-.但x0≠0,取x0=b-.对于L,当y=0时,得0=-x2+bx,即0=-x(x-b).解得x1=0,x2=b.∵
b>0,∴
右交点D的坐标为(b,0).∴
点(x0,0)与点D间的距离为b-= (4)
①
当b=2
019时,抛物线L对应的函数解析式为y=-x2+2
019x,直线a对应的函数解析式为y=x-2
019.联立上述两个解析式,可得x1=-1,x2=2
019.∴
可知每一个整数x的值都对应的一个整数y值,且-1和2
019之间(包括-1和-2
019)共有2
021个整数.∵
另外要知道所围成的封闭图形边界分两部分:线段和抛物线,∴
线段和抛物线上各有2
021个整数点.∴
总计4
042个整数点.∵
这两段图象交点有2个点重复,∴
美点”的个数为4
042-2=4
040;②
当b=2
019.5时,抛物线L对应的函数解析式为y=-x2+2
019.5x,直线a对应的函数解析式为y=x-2
019.5.联立上述两个解析式,可得x1=-1,x2=2
019.5,∴
当x取整数时,在一次函数y=x-2
019.5上,y取不到整数值.∴
在该图象上“美点”的个数为0.∵
在二次函数y=x2+2
019.5x的图象上,当x为偶数时,函数值y可取整数,可知-1到2
019.5之间有1
010个偶数,∴
“美点”共有1
010个.综上所述,当b=2
019时,“美点”的个数为4
040;当b=2
019.5时,“美点”的个数为1
010
10
一、
选择题
1.
(2019·衢州)二次函数y=(x-1)2+3图象的顶点坐标是( )
A.
(1,3)
B.
(1,-3)
C.
(-1,3)
D.
(-1,-3)
2.
(2019·重庆)抛物线y=-3x2+6x+2的对称轴是( )
A.
直线x=2
B.
直线x=-2
C.
直线x=1
D.
直线x=-1
3.
(2019·河南)已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为( )
A.
-2
B.
-4
C.
2
D.
4
4.
(2019·兰州)已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是( )
A.
2>y1>y2
B.
2>y2>y1
C.
y1>y2>2
D.
y2>y1>2
5.
(2019·哈尔滨)将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线对应的函数解析式为( )
A.
y=2(x+2)2+3
B.
y=2(x-2)2+3
C.
y=2(x-2)2-3
D.
y=2(x+2)2-3
6.
(2019·西藏)要得到函数y=-(x-1)2+1的图象,可以把函数y=-x2的图象( )
A.
向左平移1个单位长度,再向下平移1个单位长度
B.
向左平移1个单位长度,再向上平移1个单位长度
C.
向右平移1个单位长度,再向上平移1个单位长度
D.
向右平移1个单位长度,再向下平移1个单位长度
7.
(2019·百色)要得到抛物线y=x2+6x+7,可把抛物线y=x2( )
A.
先向左平移3个单位长度,再向下平移2个单位长度
B.
先向左平移6个单位长度,再向上平移7个单位长度
C.
先向左平移3个单位长度,再向上平移2个单位长度
D.
先回右平移3个单位长度,再向上平移2个单位长度
8.
(2019·雅安)在平面直角坐标系中,对于二次函数y=(x-2)2+1,下列说法错误的是( )
A.
y的最小值为1
B.
图象顶点坐标为(2,1),对称轴为直线x=2
C.
当x<2时,y的值随x值的增大而增大,当x≥2时,y的值随x值的增大而减小
D.
它的图象可以由y=x2的图象先向右平移2个单位长度,再向上平移1个单位长度得到
9.
(2019·淄博)将二次函数y=x2-4x+a的图象向左平移1个单位长度,再向上平移1个单位长度,若得到的函数图象与直线y=2有两个交点,则a的取值范围是( )
A.
a>3
B.
a<3
C.
a>5
D.
a<5
10.
(2019·河池)如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是( )
A.
ac<0
B.
b2-4ac>0
C.
2a-b=0
D.
a-b+c=0
11.
(2019·成都)如图,二次函数y=ax2+bx+c的图象经过点A(1,0),B(5,0),下列说法正确的是( )
A.
c<0
B.
b2-4ac<0
C.
a-b+c<0
D.
图象的对称轴是直线x=3
12.
(2019·沈阳)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
A.
abc<0
B.
b2-4ac<0
C.
a-b+c<0
D.
2a+b=0
13.
(2019·娄底)二次函数y=ax2+bx+c的图象如图所示,下列结论:①
abc<0;②
b2-4ac<0;③
2a>b;④
(a+c)2
1个
B.
2个
C.
3个
D.
4个
14.
(2019·鄂州)二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.
下列结论:①
abc<0;②
3a+c>0;③
(a+c)2-b2<0;④
a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
A.
1
B.
2
C.
3
D.
4
15.
(2019·通辽)在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①
abc<0;②
c+2a<0;③
9a-3b+c=0;④
a-b≥m(am+b)(m为实数);⑤
4ac-b2<0.其中错误结论的个数是( )
A.
1
B.
2
C.
3
D.
4
16.
(2019·葫芦岛)二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象大致是( )
17.
(2019·呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是( )
18.
(2019·湖州)已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )
19.
(2019·陕西)在同一平面直角坐标系中,若抛物线y=x2+(2m-1)x+2m-4与y=x2-(3m+n)x+n关于y轴对称,则符合条件的m,n的值为( )
A.
,-
B.
5,-6
C.
-1,6
D.
1,-2
20.
(2019·贵阳)如图,在平面直角坐标系中,已知点A(-1,0),点B(1,1)都在直线y=x+上,若抛物线y=ax2-x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( )
A.
a≤-2
B.
a<
C.
1≤a<或a≤-2
D.
-2≤a<
21.
(2019·玉林)如图,抛物线C:y=(x-1)2-1,顶点为D,将C沿水平方向向右(或向左)平移m个单位长度,得到抛物线C1,顶点为D1,C与C1相交于点Q,若∠DQD1=60°,则m的值为( )
A.
±4
B.
±2
C.
-2或2
D.
-4或4
22.
(2019·宜宾)已知抛物线y=x2-1与y轴交于点A,与直线y=kx(k为任意实数)相交于B,C两点,则下列结论不正确的是( )
A.
存在实数k,使得△ABC为等腰三角形
B.
存在实数k,使得△ABC的内角中有两角分别为30°和60°
C.
任意实数k,使得△ABC都为直角三角形
D.
存在实数k,使得△ABC为等边三角形
23.
(2019·福建)若二次函数y=|a|x2+bx+c的图象经过不同的五点A(m,n),B(0,y1),C(3-m,n),D(,y2),E(2,y3),则y1,y2,y3的大小关系是( )
A.
y1
y1
y3
y2
(2019·资阳)如图是函数y=x2-2x-3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A.
m≥1
B.
m≤0
C.
0≤m≤1
D.
m≥1或m≤0
25.
(2019·岳阳)对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1,x2,且x1<1
c<-3
B.
c<-2
C.
c<
D.
c<1
二、
填空题
26.
(2019·哈尔滨)二次函数y=-(x-6)2+8的最大值是________.
27.
(2019·荆州)二次函数y=-2x2-4x+5的最大值是________.
28.
(2019·白银)将二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为____________.
29.
(2019·凉山州)将抛物线y=(x-3)2-2向左平移________个单位长度后经过点A(2,2).
30.
(2019·宜宾)将抛物线y=2x2的图象,向左平移1个单位长度,再向下平移2个单位长度,所得图象对应的函数解析式为______________.
31.
(2019·广元)如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是__________.
32.
(2019·天水)二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b,N=a-b.则M,N的大小关系为M________N(填“>”“<”或“=”).
33.
(2019·荆门)抛物线y=ax2+bx+c(a,b,c为常数)的顶点为P,且抛物线经过点A(-1,0),B(m,0),C(-2,n)(1
3a+c<0;③
a(m-1)+2b>0;④
当a=-1时,存在点P使△PAB为直角三角形.其中正确的为________(填序号).
34.
(2019·镇江)已知抛物线y=ax2+4ax+4a+1(a≠0)过点A(m,3),B(n,3)两点,若线段AB的长不大于4,则代数式a2+a+1的最小值是________.
35.
(2019·内江)若x,y,z为实数,且则代数式x2-3y2+z2的最大值是________.
36.
(2019·雅安)函数y=的图象如图所示.若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为__________.
37.
(2019·大庆)如图,抛物线y=x2(p>0),点F(0,p),直线l:y=-p,已知抛物线上的点到点F的距离与到直线l的距离相等,过点F的直线与抛物线交于A,B两点,AA1⊥l,BB1⊥l,垂足分别为A1,B1,连接A1F,B1F,A1O,B1O.若A1F=a,B1F=b,则△A1OB1的面积为________(只用a,b表示).
38.
(2019·衡阳)在平面直角坐标系中,抛物线y=x2的图象如图所示.已知点A的坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4,…,依次进行下去,则点A2
019的坐标为____________.
三、
解答题
39.
(2019·宁波)如图,二次函数y=x2+ax+3的图象经过点P(-2,3).
(1)
求a的值和图象的顶点坐标.
(2)
点Q(m,n)在该二次函数图象上.
①
当m=2时,求n的值;
②
若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
第39题
40.(2019·永州)如图,抛物线经过两点A(-3,0),B(0,3),且其对称轴为直线x=-1.
(1)
求此抛物线对应的函数解析式;
(2)
若P是抛物线上点A与点B之间的动点(不包括点A,B),求△PAB面积的最大值,并求出此时点P的坐标.
第40题
41.
(2019·安徽)一次函数y=kx+4与二次函数y=ax2+c的图象的一个交点坐标为(1,2),另一个交点是该二次函数图象的顶点.
(1)
求k,a,c的值;
(2)
过点A(0,m)(0
(1)
求b,c满足的关系式;
(2)
设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式;
(3)
若该函数的图象不经过第三象限,当-5≤x≤1时,函数的最大值与最小值之差为16,求b的值.
43.(2019·南通)已知二次函数y=x2-4x+3a+2(a为常数).
(1)
请写出该二次函数的三条性质;
(2)
在同一直角坐标系中,若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,求a的取值范围.
44.(2019·北京)在平面直角坐标系xOy中,抛物线y=ax2+bx-与y轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)
求点B的坐标(用含a的式子表示);
(2)
求抛物线的对称轴;
(3)
已知点P,Q(2,2).若抛物线与线段PQ恰有一个公共点,结合图象,求a的取值范围.
45.(2019·天门)在平面直角坐标系中,已知抛物线C:y=ax2+2x-1(a≠0)和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)
若抛物线C与直线l有交点,求a的取值范围;
(2)
当a=-1,二次函数y=ax2+2x-1的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
(3)
若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
46.(2019·上海)如图,在平面直角坐标系xOy中,抛物线y=x2-2x,其顶点为A.
(1)
写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)
我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”.
①
试求抛物线y=x2-2x的“不动点”的坐标;
②
平移抛物线y=x2-2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC是梯形,求新抛物线对应的函数解析式.
第46题
47.(2019·河北)如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x-b与y轴交于点B;抛物线L:y=-x2+bx的顶点为C,且L与x轴的右交点为D.
(1)
若AB=8,求b的值,并求此时抛物线L的对称轴与直线a的交点坐标;
(2)
当点C在l下方时,求点C与l距离的最大值;
(3)
设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)
在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2
019和b=2
019.5时“美点”的个数.
第47题
参考答案
一、
A
C
B
A
B
C
A
C
D
C
D
D
A
C
A
D
D
D
D
C
A
D
D
C
B
二、
8
7
y=(x-2)2+1
3
y=2(x+1)2-2
-6
②③
26
0
(-1
010,1
0102)
三、
(1)
把点P(-2,3)代入y=x2+ax+3中,得3=4-2a+3,解得a=2.∴
二次函数的解析式为y=x2+2x+3=(x+1)2+2.∴
顶点坐标为(-1,2) (2)
①
当m=2时,n=(2+1)2+2=11 ②
∵
点Q到y轴的距离小于2,∴
|m|<2.∴
-2
(1)
∵
抛物线的对称轴是直线x=-1,且经过点A(-3,0),∴
由抛物线的对称性可知,抛物线还经过点(1,0).设抛物线对应的函数解析式为y=a(x-1)(x+3),把B(0,3)代入,得3=-3a,解得a=-1.∴
抛物线对应的函数解析式为y=-x2-2x+3 (2)
设直线AB对应的函数解析式为y=kx+b,∵
点A(-3,0),B(0,3)在直线y=kx+b上,∴
解得∴
直线AB对应的函数解析式为y=x+3.过点P作PQ⊥x轴于点Q,交直线AB于点M,设P(x,-x2-2x+3),则M(x,x+3),∴
PM=-x2-2x+3-(x+3)=-x2-3x.∴
S△PAB=(-x2-3x)×3=-(x+)2+.当x=-时,S△PAB有最大值,为,此时点P的纵坐标为--2×+3=,∴
△PAB面积的最大值为,此时点P的坐标为
(1)
根据题意,得二次函数y=ax2+c的图象的顶点坐标为(0,c).将点(0,c),(1,2)代入一次函数的解析式,得解得将点(1,2)代入y=ax2+4,得2=a+4,解得a=-2.∴
k的值为-2,a的值为-2,c的值为4 (2)
由(1)可知,二次函数的解析式为y=-2x2+4.令y=m,得2x2+m-4=0,解得x=±.设B,C两点的坐标分别为(x1,m),(x2,m),则BC=|x1-x2|=2.∴
W=OA2+BC2=m2+4×=m2-2m+8=(m-1)2+7.∵
0
(1)
将点(-2,4)代入y=x2+bx+c,得4=4-2b+c,即-2b+c=0,∴
c=2b (2)
根据题意,得m=-,n=.∴
b=-2m.又由(1)知,c=2b,∴
c=-4m.∴
n===-m2-4m (3)
如图,由(2)的结论,画出函数y=x2+bx+c和函数y=-x2-4x的图象.∵
函数y=x2+bx+c的图象不经过第三象限,∴
-4≤-≤0.①
当-4≤-≤-2,即4≤b≤8时,如图①.当x=1时,函数取到最大值,为1+3b;当x=-时,函数取到最小值,为.∴
1+3b-=16,即b2+4b-60=0,解得b1=6,b2=-10(不合题意,舍去).②
当-2<-≤0,即0≤b<4时,如图②.当x=-5时,函数取到最大值,为25-3b;当x=-时,函数取到最小值,为,∴
25-3b-=16,即b2-20b+36=0,解得b1=2,b2=18(不合题意,舍去).综上所述,b的值为2或6
(1)
答案不唯一,如①
图象开口向上;②
图象的对称轴为直线x=2;③
当x>2时,y随x的增大而增大 (2)
∵
二次函数的图象与一次函数y=2x-1的图象有两个交点,∴
x2-4x+3a+2=2x-1,即x2-6x+3a+3=0.∴
Δ=36-4(3a+3)=-12a+24>0,解得a<2.∵
二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点,∴
二次函数y=x2-6x+3a+3的图象与x轴x≤4的部分有两个交点.结合图象(图略)可知,当x=4时,x2-6x+3a+3≥0.∴
当x=4时,x2-6x+3a+3=3a-5≥0,解得a≥.∴
当二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点时,a的取值范围为≤a<2
(1)
由题意,得A,又∵
将点A向右平移2个单位长度,得到点B,∴
B (2)
∵
点A与点B关于直线x=1对称,点A,B均在抛物线上,∴
抛物线的对称轴为直线x=1 (3)
①
当a>0时,则-<0.结合图象(图略)可知,此时线段PQ与抛物线没有交点.②
当a<0时,则->0.结合图象(图略)可知,此时-≤2,解得a≤-.综上所述,当a≤-时,抛物线与线段PQ恰有一个公共点
(1)
将点A(-3,-3),B(1,-1)代入y=kx+b,得解得∴
直线l对应的函数解析式为y=x-.联立y=ax2+2x-1与y=x-,得2ax2+3x+1=0.∵
抛物线C与直线l有交点,∴
Δ=9-8a≥0,解得a≤.又∵
a≠0,∴
a的取值范围为a≤且a≠0 (2)
根据题意,得二次函数的解析式为y=-x2+2x-1=-(x-1)2.∵
-1<0,∴
二次函数的图象开口向下,对称轴为直线x=1.∵
当m≤x≤m+2时,y有最大值-4,∴
当y=-4时,有-(x-1)2=-4,解得x=-1或x=3.①
当x<1时,y随x的增大而增大,∴
当x=m+2=-1时,y有最大值-4,此时m=-3;②
当x>1时,y随x的增大而减小,∴
当x=m=3时,y有最大值-4.综上所述,m的值为-3或3 (3)
≤a<或a≤-2
(1)
对于抛物线y=x2-2x=(x-1)2-1,其开口向上,顶点A的坐标为(1,-1);当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小 (2)
①
设抛物线“不动点”坐标为(t,t),则t=t2-2t.解得t=0或3.∴
“不动点”的坐标为(0,0)或(3,3) ②
∵
新抛物线顶点B为“不动点”,则设点B(m,m),∴
新抛物线的对称轴为直线x=m,与x轴的交点C的坐标为(m,0).∵
四边形OABC是梯形,∴
直线x=m在y轴左侧.∵
BC与OA不平行,∴
OC∥AB.又∵
点A的坐标为(1,-1),点B的坐标为(m,m),∴
m=-1.∴
新抛物线是由抛物线y=x2-2x向左平移2个单位长度得到的.∴
新抛物线对应的函数表达式为y=(x+1)2-1
(1)
当x=0时,y=x-b=-b,∴
点B的坐标为(0,-b).∵
AB=8,而点A的坐标为(0,b),∴
b-(-b)=8.解得b=4.∴
抛物线L对应的函数解析式为y=-x2+4x.∴
抛物线L的对称轴为直线x=2.当x=2时,y=x-4=-2.∴
抛物线L的对称轴与直线a的交点坐标为(2,-2
) (2)
∵
y=-x2+bx=-+,∴
抛物线L的顶点C的坐标为.∵
点C在l下方,∴
C与l的距离为b-=-(b-2)2+1≤1.∴
点C与l距离的最大值为1 (3)
由题意,得y3=,即y1+y2=2y3,得b+x0-b=2(-x+bx0).解得x0=0或x0=b-.但x0≠0,取x0=b-.对于L,当y=0时,得0=-x2+bx,即0=-x(x-b).解得x1=0,x2=b.∵
b>0,∴
右交点D的坐标为(b,0).∴
点(x0,0)与点D间的距离为b-= (4)
①
当b=2
019时,抛物线L对应的函数解析式为y=-x2+2
019x,直线a对应的函数解析式为y=x-2
019.联立上述两个解析式,可得x1=-1,x2=2
019.∴
可知每一个整数x的值都对应的一个整数y值,且-1和2
019之间(包括-1和-2
019)共有2
021个整数.∵
另外要知道所围成的封闭图形边界分两部分:线段和抛物线,∴
线段和抛物线上各有2
021个整数点.∴
总计4
042个整数点.∵
这两段图象交点有2个点重复,∴
美点”的个数为4
042-2=4
040;②
当b=2
019.5时,抛物线L对应的函数解析式为y=-x2+2
019.5x,直线a对应的函数解析式为y=x-2
019.5.联立上述两个解析式,可得x1=-1,x2=2
019.5,∴
当x取整数时,在一次函数y=x-2
019.5上,y取不到整数值.∴
在该图象上“美点”的个数为0.∵
在二次函数y=x2+2
019.5x的图象上,当x为偶数时,函数值y可取整数,可知-1到2
019.5之间有1
010个偶数,∴
“美点”共有1
010个.综上所述,当b=2
019时,“美点”的个数为4
040;当b=2
019.5时,“美点”的个数为1
010
