人教版八年级数学下册第十八章 平行四边形单元测试题(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册第十八章 平行四边形单元测试题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 136.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 07:20:17 | ||
图片预览


文档简介
第十八章 平行四边形
一、选择题(每小题5分,共35分)
1.下列命题中,是真命题的为
( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.若菱形ABCD的对角线AC,BD的长分别是5
cm,12
cm,则菱形ABCD的面积是
( )
A.30
cm2
B.36
cm2
C.48
cm2
D.60
cm2
3.如图1,在Rt△ABC中,∠ACB=90°,D,E,F分别为AB,AC,BC的中点,则CD和EF的大小关系是
( )
图1
A.CD>EF
B.CDC.CD=EF
D.无法比较
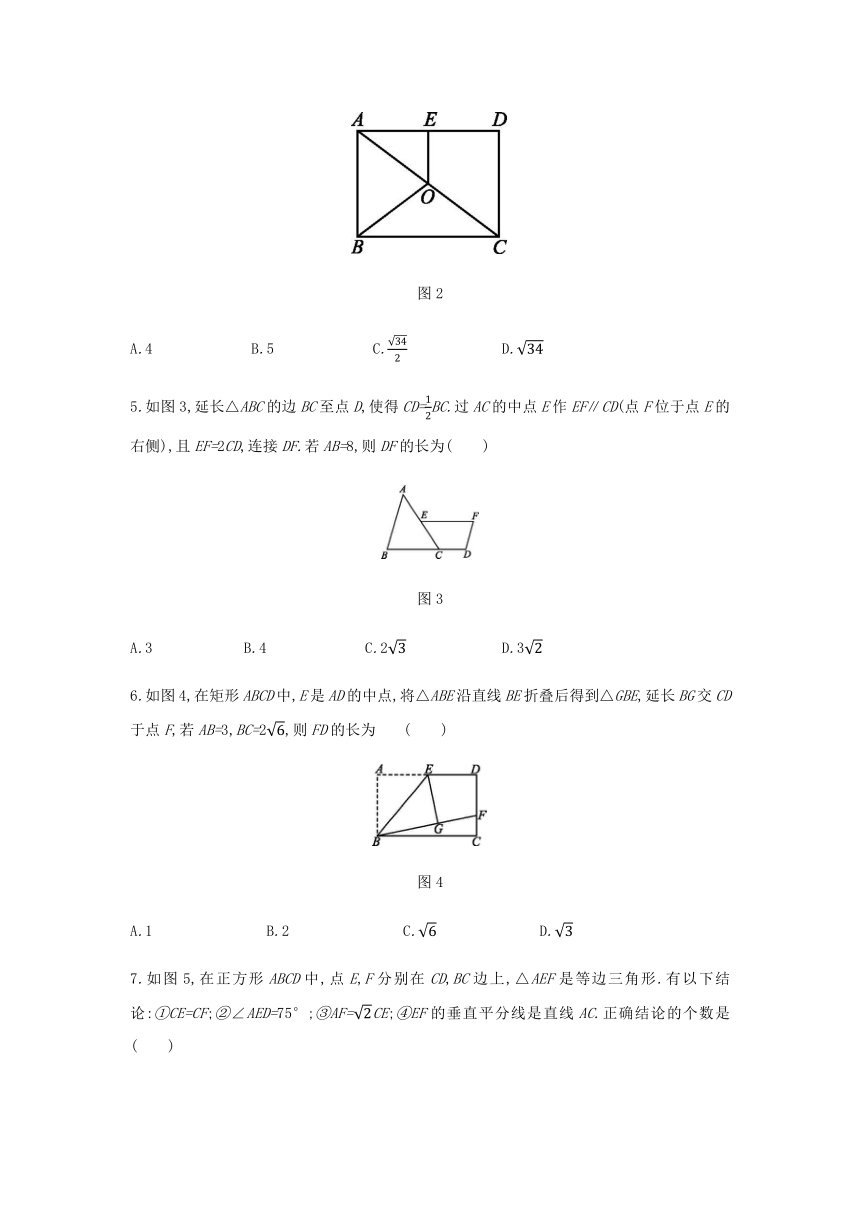
4.如图2所示,O是矩形ABCD的对角线AC的中点,OE∥AB交AD于点E.若OE=3,BC=8,则OB的长为
( )
图2
A.4
B.5
C.
D.
5.如图3,延长△ABC的边BC至点D,使得CD=BC.过AC的中点E作EF∥CD(点F位于点E的右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
图3
A.3
B.4
C.2
D.3
6.如图4,在矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=3,BC=2,则FD的长为
( )
图4
A.1
B.2
C.
D.
7.如图5,在正方形ABCD中,点E,F分别在CD,BC边上,△AEF是等边三角形.有以下结论:①CE=CF;②∠AED=75°;③AF=CE;④EF的垂直平分线是直线AC.正确结论的个数是
( )
图5
A.1
B.2
C.3
D.4
二、填空题(每小题5分,共30分)
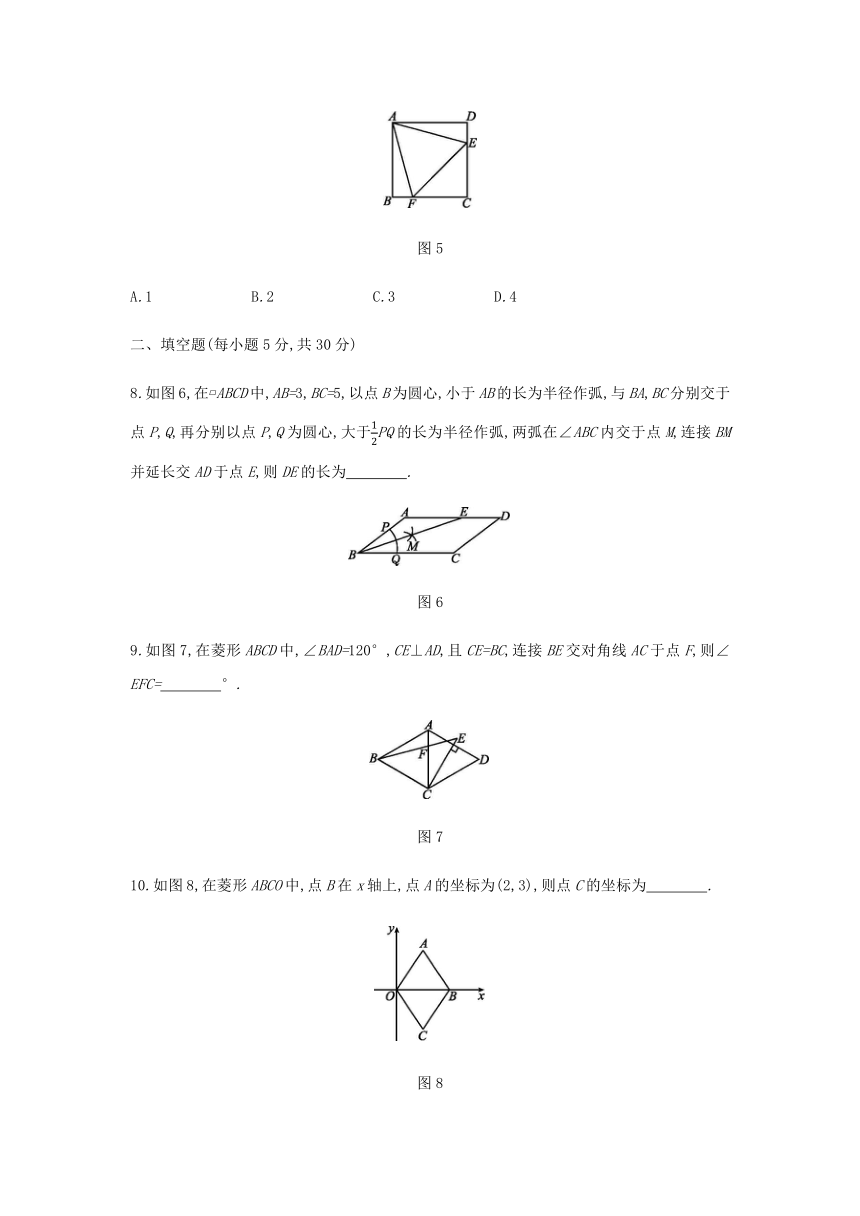
8.如图6,在?ABCD中,AB=3,BC=5,以点B为圆心,小于AB的长为半径作弧,与BA,BC分别交于点P,Q,再分别以点P,Q为圆心,大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .?
图6
9.如图7,在菱形ABCD中,∠BAD=120°,CE⊥AD,且CE=BC,连接BE交对角线AC于点F,则∠EFC= °.?
图7
10.如图8,在菱形ABCO中,点B在x轴上,点A的坐标为(2,3),则点C的坐标为 .?
图8
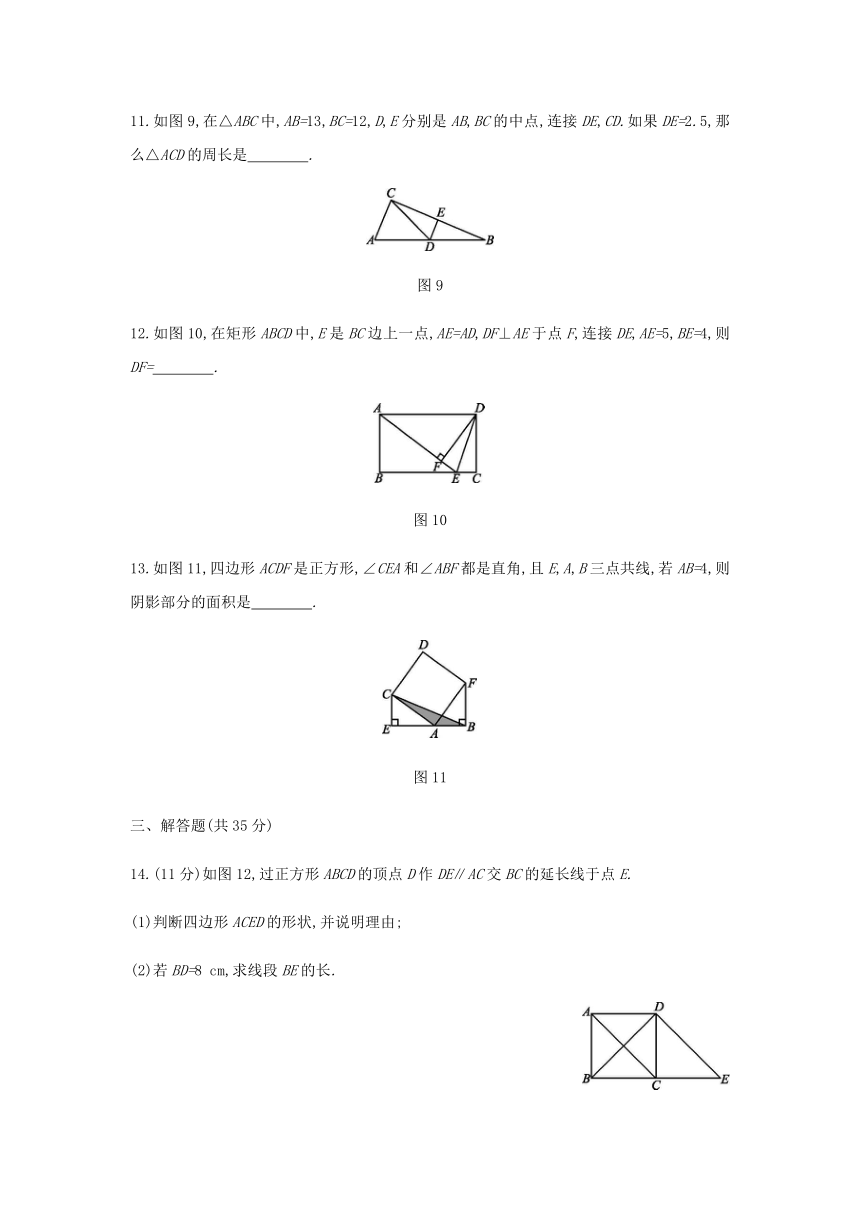
11.如图9,在△ABC中,AB=13,BC=12,D,E分别是AB,BC的中点,连接DE,CD.如果DE=2.5,那么△ACD的周长是 .?
图9
12.如图10,在矩形ABCD中,E是BC边上一点,AE=AD,DF⊥AE于点F,连接DE,AE=5,BE=4,则DF= .?
图10
13.如图11,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且E,A,B三点共线,若AB=4,则阴影部分的面积是 .?
图11
三、解答题(共35分)
14.(11分)如图12,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8
cm,求线段BE的长.
图12
15.(12分)如图13,在矩形ABCD中,E,F分别是AD,BC边的中点,CE,AF分别交BD于G,H两点.
(1)求证:四边形AFCE是平行四边形;
(2)CG与AH的数量关系是 .?
图13
16.(12分)如图14,在菱形ABCD中,点E,F在对角线AC上,且AE=CF.
(1)求证:△ABE≌△ADE;
(2)求证:四边形BFDE是菱形;
(3)若AC=4,BD=8,AE=,请求出四边形BFDE的面积.
图14
参考答案
1.D
2.A [解析]
∵菱形的对角线AC,BD的长分别为5
cm,12
cm,
∴菱形ABCD的面积=AC·BD=×5×12=30(cm2).
3.C [解析]
∵E,F分别为AC,BC的中点,∴EF=AB.∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴CD=AB,∴CD=EF.
4.B [解析]
连接OD.∵O是矩形ABCD的对角线AC的中点,
∴B,O,D三点共线且OA=OC=OB=OD.
∵OE∥AB,AB⊥AD,∴OE⊥AD.
又∵OA=OD,∴AE=ED=AD=BC=4.
在Rt△AOE中,OA===5,
∴OB=OA=5.
5.B [解析]
如图,取AB的中点M,连接ME,则ME∥BC,ME=BC.∵EF∥CD,∴M,E,F三点共线.∵EF=2CD,CD=BC,∴MF=BD,∴四边形MBDF是平行四边形,∴DF=BM=4.故选B.
6.B [解析]
连接EF.
∵E是AD的中点,
∴AE=DE.
∵△ABE沿BE折叠后得到△GBE,
∴AE=EG,AB=BG,∠EGB=∠A,
∴ED=EG.
∵在矩形ABCD中,∠A=∠D=90°,
∴∠EGF=90°.
在Rt△EDF和Rt△EGF中,
∴Rt△EDF≌Rt△EGF(HL),
∴DF=FG.
设DF=x,则BF=3+x,CF=3-x.
在Rt△BCF中,BC2+CF2=BF2,即(2)2+(3-x)2=(3+x)2,
解得x=2,即DF=2.
7.D [解析]
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=90°.
∵△AEF是等边三角形,
∴AE=AF=EF,∠AEF=60°.
在Rt△ABF和Rt△ADE中,
∴Rt△ABF≌Rt△ADE,
∴BF=DE,
∴CD-DE=BC-BF,
即CE=CF,
故①正确.
∵CE=CF,∠C=90°,
∴EF=CE,∠CEF=45°,
∴AF=CE,∠AED=180°-∠CEF-∠AEF=75°,
故②③正确.
∵AE=AF,CE=CF,
∴AC垂直平分EF,
故④正确.
8.2 [解析]
根据作图的方法得:BE平分∠ABC,∴∠ABE=∠CBE.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴DE=AD-AE=5-3=2.
故答案为2.
9.105 [解析]
∵四边形ABCD为菱形,∠BAD=120°,
∴CD=AD,∠ACB=∠ACD=∠BCD=∠BAD=60°,
∴△ACD是等边三角形.
∵CE⊥AD,
∴∠ACE=∠ACD=30°,
∴∠BCE=∠ACB+∠ACE=90°.
∵CE=BC,
∴∠E=45°,
∴∠EFC=180°-∠E-∠ACE=180°-45°-30°=105°.
10.(2,-3) [解析]
关于x轴对称的两个点的坐标特征:横坐标相同,纵坐标互为相反数.由题意知,点A与点C关于x轴对称,点A的坐标为(2,3),故点C的坐标为(2,-3).
11.18 [解析]
由于DE是△ABC的中位线,所以AC=5,由于AB=13,BC=12,52+122=132,因此△ABC是直角三角形,∠ACB=90°,故CD是Rt△ABC斜边AB上的中线,因此CD=AB=6.5,而AD=6.5,AC=5,所以△ACD的周长是6.5+6.5+5=18.
12.3 [解析]
∵四边形ABCD为矩形,
∴AD∥BC,且∠B=90°,
∴∠DAF=∠BEA.
∵DF⊥AE,
∴∠DFA=∠B=90°.
在△ADF和△EAB中,
∴△ADF≌△EAB(AAS),
∴AF=BE=4.
在Rt△ADF中,∵AD=AE=5,
∴DF===3.
13.8 [解析]
∵四边形ACDF是正方形,
∴AC=FA,∠CAF=90°,
∴∠CAE+∠BAF=90°.
又∵∠CEA是直角,
∴∠CAE+∠ECA=90°,
∴∠ECA=∠BAF.
在△ACE和△FAB中,
∴△ACE≌△FAB(AAS),
∴AB=CE=4,
∴S△ABC=AB·CE=×4×4=8.
14.
解:(1)四边形ACED是平行四边形.
理由如下:
∵四边形ABCD是正方形,∴AD∥BC.
又∵DE∥AC,
∴四边形ACED是平行四边形.
(2)由(1)可得AD=CE.
∵四边形ABCD是正方形,BD=8
cm,
∴BC=AD=4
cm,
∴BE=BC+CE=2BC=8
cm.
15.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.
∵E,F分别是AD,BC边的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AFCE是平行四边形.
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGC=∠GHF=∠BHA.
∵CD∥AB,
∴∠CDG=∠ABH.
在△DCG和△BAH中,
∴△DCG≌△BAH(AAS),
∴CG=AH.
16.解:(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠BAE=∠DAE.
在△ABE和△ADE中,
∴△ABE≌△ADE(SAS).
(2)证明:设AC与BD的交点为O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD.
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF.
又∵OB=OD,
∴四边形BFDE是平行四边形.
又∵EF⊥BD,
∴四边形BFDE是菱形.
(3)∵AC=4,AE=,AE=CF,
∴EF=AC-2AE=4-2=2.
由(2)知,四边形BFDE是菱形,
∴四边形BFDE的面积=EF·BD=×2×8=8.
一、选择题(每小题5分,共35分)
1.下列命题中,是真命题的为
( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.若菱形ABCD的对角线AC,BD的长分别是5
cm,12
cm,则菱形ABCD的面积是
( )
A.30
cm2
B.36
cm2
C.48
cm2
D.60
cm2
3.如图1,在Rt△ABC中,∠ACB=90°,D,E,F分别为AB,AC,BC的中点,则CD和EF的大小关系是
( )
图1
A.CD>EF
B.CD
D.无法比较
4.如图2所示,O是矩形ABCD的对角线AC的中点,OE∥AB交AD于点E.若OE=3,BC=8,则OB的长为
( )
图2
A.4
B.5
C.
D.
5.如图3,延长△ABC的边BC至点D,使得CD=BC.过AC的中点E作EF∥CD(点F位于点E的右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
图3
A.3
B.4
C.2
D.3
6.如图4,在矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=3,BC=2,则FD的长为
( )
图4
A.1
B.2
C.
D.
7.如图5,在正方形ABCD中,点E,F分别在CD,BC边上,△AEF是等边三角形.有以下结论:①CE=CF;②∠AED=75°;③AF=CE;④EF的垂直平分线是直线AC.正确结论的个数是
( )
图5
A.1
B.2
C.3
D.4
二、填空题(每小题5分,共30分)
8.如图6,在?ABCD中,AB=3,BC=5,以点B为圆心,小于AB的长为半径作弧,与BA,BC分别交于点P,Q,再分别以点P,Q为圆心,大于PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .?
图6
9.如图7,在菱形ABCD中,∠BAD=120°,CE⊥AD,且CE=BC,连接BE交对角线AC于点F,则∠EFC= °.?
图7
10.如图8,在菱形ABCO中,点B在x轴上,点A的坐标为(2,3),则点C的坐标为 .?
图8
11.如图9,在△ABC中,AB=13,BC=12,D,E分别是AB,BC的中点,连接DE,CD.如果DE=2.5,那么△ACD的周长是 .?
图9
12.如图10,在矩形ABCD中,E是BC边上一点,AE=AD,DF⊥AE于点F,连接DE,AE=5,BE=4,则DF= .?
图10
13.如图11,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且E,A,B三点共线,若AB=4,则阴影部分的面积是 .?
图11
三、解答题(共35分)
14.(11分)如图12,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8
cm,求线段BE的长.
图12
15.(12分)如图13,在矩形ABCD中,E,F分别是AD,BC边的中点,CE,AF分别交BD于G,H两点.
(1)求证:四边形AFCE是平行四边形;
(2)CG与AH的数量关系是 .?
图13
16.(12分)如图14,在菱形ABCD中,点E,F在对角线AC上,且AE=CF.
(1)求证:△ABE≌△ADE;
(2)求证:四边形BFDE是菱形;
(3)若AC=4,BD=8,AE=,请求出四边形BFDE的面积.
图14
参考答案
1.D
2.A [解析]
∵菱形的对角线AC,BD的长分别为5
cm,12
cm,
∴菱形ABCD的面积=AC·BD=×5×12=30(cm2).
3.C [解析]
∵E,F分别为AC,BC的中点,∴EF=AB.∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴CD=AB,∴CD=EF.
4.B [解析]
连接OD.∵O是矩形ABCD的对角线AC的中点,
∴B,O,D三点共线且OA=OC=OB=OD.
∵OE∥AB,AB⊥AD,∴OE⊥AD.
又∵OA=OD,∴AE=ED=AD=BC=4.
在Rt△AOE中,OA===5,
∴OB=OA=5.
5.B [解析]
如图,取AB的中点M,连接ME,则ME∥BC,ME=BC.∵EF∥CD,∴M,E,F三点共线.∵EF=2CD,CD=BC,∴MF=BD,∴四边形MBDF是平行四边形,∴DF=BM=4.故选B.
6.B [解析]
连接EF.
∵E是AD的中点,
∴AE=DE.
∵△ABE沿BE折叠后得到△GBE,
∴AE=EG,AB=BG,∠EGB=∠A,
∴ED=EG.
∵在矩形ABCD中,∠A=∠D=90°,
∴∠EGF=90°.
在Rt△EDF和Rt△EGF中,
∴Rt△EDF≌Rt△EGF(HL),
∴DF=FG.
设DF=x,则BF=3+x,CF=3-x.
在Rt△BCF中,BC2+CF2=BF2,即(2)2+(3-x)2=(3+x)2,
解得x=2,即DF=2.
7.D [解析]
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=90°.
∵△AEF是等边三角形,
∴AE=AF=EF,∠AEF=60°.
在Rt△ABF和Rt△ADE中,
∴Rt△ABF≌Rt△ADE,
∴BF=DE,
∴CD-DE=BC-BF,
即CE=CF,
故①正确.
∵CE=CF,∠C=90°,
∴EF=CE,∠CEF=45°,
∴AF=CE,∠AED=180°-∠CEF-∠AEF=75°,
故②③正确.
∵AE=AF,CE=CF,
∴AC垂直平分EF,
故④正确.
8.2 [解析]
根据作图的方法得:BE平分∠ABC,∴∠ABE=∠CBE.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=5,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∴DE=AD-AE=5-3=2.
故答案为2.
9.105 [解析]
∵四边形ABCD为菱形,∠BAD=120°,
∴CD=AD,∠ACB=∠ACD=∠BCD=∠BAD=60°,
∴△ACD是等边三角形.
∵CE⊥AD,
∴∠ACE=∠ACD=30°,
∴∠BCE=∠ACB+∠ACE=90°.
∵CE=BC,
∴∠E=45°,
∴∠EFC=180°-∠E-∠ACE=180°-45°-30°=105°.
10.(2,-3) [解析]
关于x轴对称的两个点的坐标特征:横坐标相同,纵坐标互为相反数.由题意知,点A与点C关于x轴对称,点A的坐标为(2,3),故点C的坐标为(2,-3).
11.18 [解析]
由于DE是△ABC的中位线,所以AC=5,由于AB=13,BC=12,52+122=132,因此△ABC是直角三角形,∠ACB=90°,故CD是Rt△ABC斜边AB上的中线,因此CD=AB=6.5,而AD=6.5,AC=5,所以△ACD的周长是6.5+6.5+5=18.
12.3 [解析]
∵四边形ABCD为矩形,
∴AD∥BC,且∠B=90°,
∴∠DAF=∠BEA.
∵DF⊥AE,
∴∠DFA=∠B=90°.
在△ADF和△EAB中,
∴△ADF≌△EAB(AAS),
∴AF=BE=4.
在Rt△ADF中,∵AD=AE=5,
∴DF===3.
13.8 [解析]
∵四边形ACDF是正方形,
∴AC=FA,∠CAF=90°,
∴∠CAE+∠BAF=90°.
又∵∠CEA是直角,
∴∠CAE+∠ECA=90°,
∴∠ECA=∠BAF.
在△ACE和△FAB中,
∴△ACE≌△FAB(AAS),
∴AB=CE=4,
∴S△ABC=AB·CE=×4×4=8.
14.
解:(1)四边形ACED是平行四边形.
理由如下:
∵四边形ABCD是正方形,∴AD∥BC.
又∵DE∥AC,
∴四边形ACED是平行四边形.
(2)由(1)可得AD=CE.
∵四边形ABCD是正方形,BD=8
cm,
∴BC=AD=4
cm,
∴BE=BC+CE=2BC=8
cm.
15.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.
∵E,F分别是AD,BC边的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AFCE是平行四边形.
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGC=∠GHF=∠BHA.
∵CD∥AB,
∴∠CDG=∠ABH.
在△DCG和△BAH中,
∴△DCG≌△BAH(AAS),
∴CG=AH.
16.解:(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠BAE=∠DAE.
在△ABE和△ADE中,
∴△ABE≌△ADE(SAS).
(2)证明:设AC与BD的交点为O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD.
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF.
又∵OB=OD,
∴四边形BFDE是平行四边形.
又∵EF⊥BD,
∴四边形BFDE是菱形.
(3)∵AC=4,AE=,AE=CF,
∴EF=AC-2AE=4-2=2.
由(2)知,四边形BFDE是菱形,
∴四边形BFDE的面积=EF·BD=×2×8=8.
