24.2.2直线和圆的位置关系(1)
文档属性
| 名称 | 24.2.2直线和圆的位置关系(1) |
|
|
| 格式 | zip | ||
| 文件大小 | 217.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-08 00:00:00 | ||
图片预览

文档简介
花山中学 九年级数学 学科导学案 班级: 姓名:
课题: 24.2.2直线和圆的位置关系(1) 主备人: 杨鸿飞 备课组长签字: 教研组长签字: 教务处审核:
学习目标: 1、知道直线和圆的三种位置关系。 2、会根据d与R的大小判断直线和圆的位置关系. 。
沉默是金难买课堂一分,跃跃欲试不如亲身尝试! 面对困难别退缩,相信自己一定行!
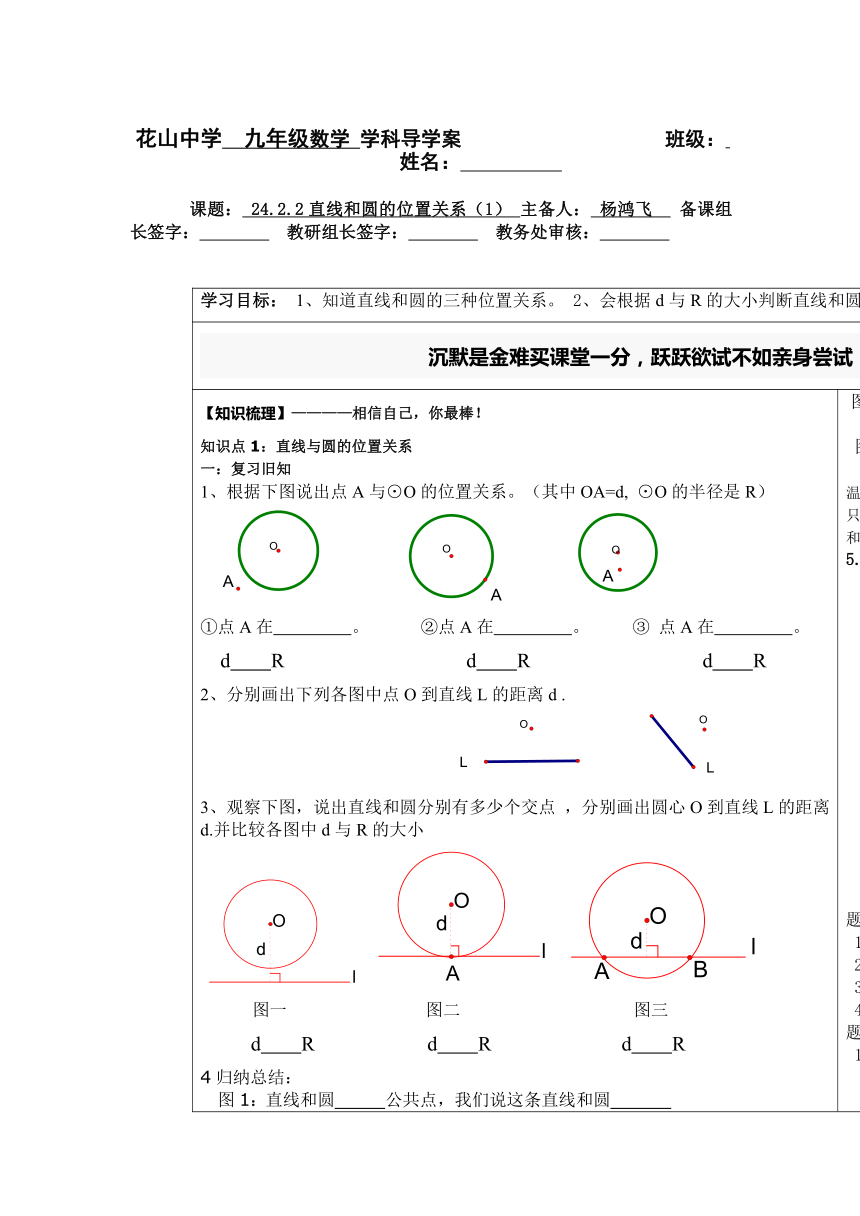
【知识梳理】————相信自己,你最棒!知识点1:直线与圆的位置关系一:复习旧知1、根据下图说出点A与⊙O的位置关系。(其中OA=d, ⊙O的半径是R)①点A在 。 ②点A在 。 ③ 点A在 。d R d R d R2、分别画出下列各图中点O到直线L的距离d .3、观察下图,说出直线和圆分别有多少个交点 ,分别画出圆心O到直线L的距离d.并比较各图中d与R的大小 图一 图二 图三d R d R d R4归纳总结: 图1:直线和圆 公共点,我们说这条直线和圆 2、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相切或相交【能力提升】——集体的智慧是无穷的,携手解决下面的问题吧!1. 已知圆心和直线的距离为4cm,如果圆和直线的关系分别为以下情况,那么圆的直径应分别取怎样的值?为什么 (1)相交;(2)相切;(3)相离。 2. 在RtABC中, C=90°, AC=3cm, BC=4cm, 以C为圆心, r 为半径的圆与AB有怎样的位置关系 为什么 (1) r =2cm ; (2) r =2.4cm ; (3) r =3cm. 思考:1、什么叫点到直线的距离? 2、要判断圆与AB的位置关系须比较什么? 3、故应求什么?怎么做? 4、要求CD, 应考虑用什么方法? 解答过程: 3. 如图:已知∠ AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?(1)r=2cm; (2)r=4cm; (3)r=2.5cm. 图2:直线和圆只有 公共点,我们说这条直线和圆 ,直线L叫做圆O的 ,这个公共点叫 图3:直线和圆有 公共点,我们说这条直线和圆 。直线L叫做圆O的 。温馨提示:理解切线的定义时,要明确直线和圆有唯一公共点的含义。“唯一公共点”就是有且只有一个公共点,与有一个公共点的含义不同,避免出现“直线和圆有一个公共点时,即为直线和圆相切”的错误,要用动态的观点及数形结合法的思想理解本节的概念。5.补充下表题型一:是是非非1、直线与圆最多有两个公共点 。( ) 2、若C为⊙O上的一点,则过点C的直线与⊙O相切。( )3、 若A、B是⊙O外两点, 则直线AB 与⊙O相离。( ) 4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )题型二:选择1、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为( )A、d≤4 B、d<4 C、d≥4 D、d=4【中考链接】———一份耕耘,一份收获(1)圆心O到直线l的距离为d,⊙O的半径为R,若d、R是方程x2-4x+m=0的两根,且直线l与⊙O相切,则m的值是________.(2006.山东)(2)设⊙O的半径为r,点O到直线l的距离为d,若⊙O与l最多只有一个公共点,则d与r的关系为_________.(2005.河北) (3)在△ABC中,AD为BC边上的高,AD=1/2BC,E、F分别是AB、AC的中点,则以EF为直径的圆与BC的位置关系是_____. (2005.河南) 规律总结:判断直线和圆的位置关系可以根据:1,直线和圆的公共点个数 2,圆心到直线的距离和半径的关系
课题: 24.2.2直线和圆的位置关系(1) 主备人: 杨鸿飞 备课组长签字: 教研组长签字: 教务处审核:
学习目标: 1、知道直线和圆的三种位置关系。 2、会根据d与R的大小判断直线和圆的位置关系. 。
沉默是金难买课堂一分,跃跃欲试不如亲身尝试! 面对困难别退缩,相信自己一定行!
【知识梳理】————相信自己,你最棒!知识点1:直线与圆的位置关系一:复习旧知1、根据下图说出点A与⊙O的位置关系。(其中OA=d, ⊙O的半径是R)①点A在 。 ②点A在 。 ③ 点A在 。d R d R d R2、分别画出下列各图中点O到直线L的距离d .3、观察下图,说出直线和圆分别有多少个交点 ,分别画出圆心O到直线L的距离d.并比较各图中d与R的大小 图一 图二 图三d R d R d R4归纳总结: 图1:直线和圆 公共点,我们说这条直线和圆 2、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相切或相交【能力提升】——集体的智慧是无穷的,携手解决下面的问题吧!1. 已知圆心和直线的距离为4cm,如果圆和直线的关系分别为以下情况,那么圆的直径应分别取怎样的值?为什么 (1)相交;(2)相切;(3)相离。 2. 在RtABC中, C=90°, AC=3cm, BC=4cm, 以C为圆心, r 为半径的圆与AB有怎样的位置关系 为什么 (1) r =2cm ; (2) r =2.4cm ; (3) r =3cm. 思考:1、什么叫点到直线的距离? 2、要判断圆与AB的位置关系须比较什么? 3、故应求什么?怎么做? 4、要求CD, 应考虑用什么方法? 解答过程: 3. 如图:已知∠ AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?(1)r=2cm; (2)r=4cm; (3)r=2.5cm. 图2:直线和圆只有 公共点,我们说这条直线和圆 ,直线L叫做圆O的 ,这个公共点叫 图3:直线和圆有 公共点,我们说这条直线和圆 。直线L叫做圆O的 。温馨提示:理解切线的定义时,要明确直线和圆有唯一公共点的含义。“唯一公共点”就是有且只有一个公共点,与有一个公共点的含义不同,避免出现“直线和圆有一个公共点时,即为直线和圆相切”的错误,要用动态的观点及数形结合法的思想理解本节的概念。5.补充下表题型一:是是非非1、直线与圆最多有两个公共点 。( ) 2、若C为⊙O上的一点,则过点C的直线与⊙O相切。( )3、 若A、B是⊙O外两点, 则直线AB 与⊙O相离。( ) 4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )题型二:选择1、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为( )A、d≤4 B、d<4 C、d≥4 D、d=4【中考链接】———一份耕耘,一份收获(1)圆心O到直线l的距离为d,⊙O的半径为R,若d、R是方程x2-4x+m=0的两根,且直线l与⊙O相切,则m的值是________.(2006.山东)(2)设⊙O的半径为r,点O到直线l的距离为d,若⊙O与l最多只有一个公共点,则d与r的关系为_________.(2005.河北) (3)在△ABC中,AD为BC边上的高,AD=1/2BC,E、F分别是AB、AC的中点,则以EF为直径的圆与BC的位置关系是_____. (2005.河南) 规律总结:判断直线和圆的位置关系可以根据:1,直线和圆的公共点个数 2,圆心到直线的距离和半径的关系
同课章节目录
