求曲线的轨迹方程
图片预览




文档简介
(共18张PPT)
欢迎光临指导
课题的引入
一 平面解析几何研究的主要问题
由已知条件求曲线方程
通过曲线方程研究曲线的性质
二 求轨迹方程问题的类型
第一类 已知曲线形状
第二类 未知曲线形状
三 求轨迹方程的常见方法
直接法、定义法、代换法、
参数法、交轨法、复数法
【教学目标】
常用点的轨迹。
求动点的轨迹的常用方法与技巧.
通过对求轨迹方程的学习,培养学生综合运用各方面知识的能力.
【教学重点】
求动点的轨迹的常用方法与技巧.
【教学难点】
用代换法求动点的轨迹方法与技巧.
求曲线的轨迹方程(1)
复面解析几何研究的两大主要问题.
求曲线方程的一般步骤.
建系设点.
写出点集.
列方程.
化简方程.
检验方程.
二 求轨迹方程的常用方法
1.直接法
由题设所给(或通过分析图形的几何性质而得出)的动点所满足的几何条件列出等式,再用坐标代替这些等式,化简得曲线的方程,这种方法叫直接法。
x
y
o
k
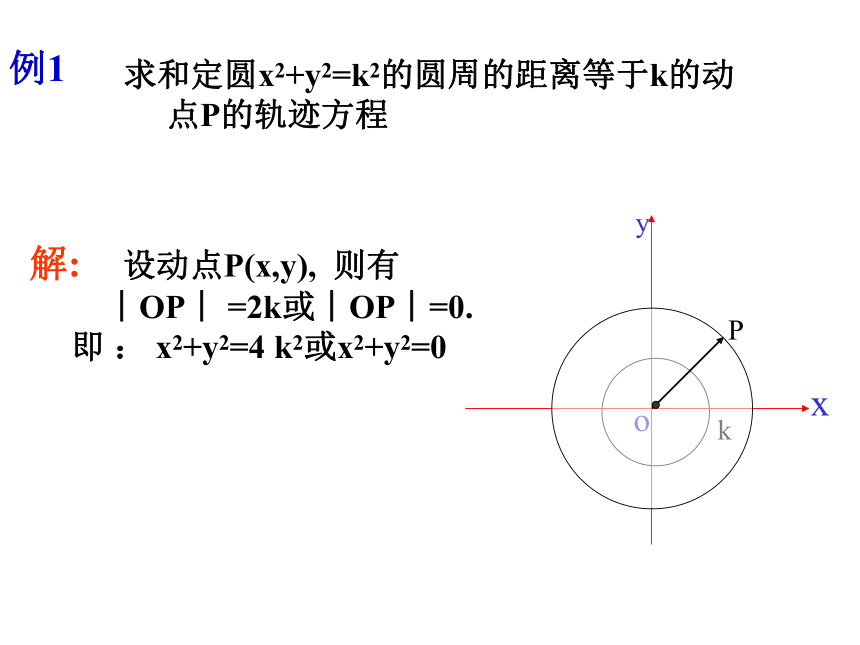
例1
求和定圆x2+y2=k2的圆周的距离等于k的动点P的轨迹方程
P
解: 设动点P(x,y), 则有
︱OP︱ =2k或︱OP︱=0.
即 : x2+y2=4 k2或x2+y2=0
A:\1.GSP
B
M
X
Y
O
-6
A
P
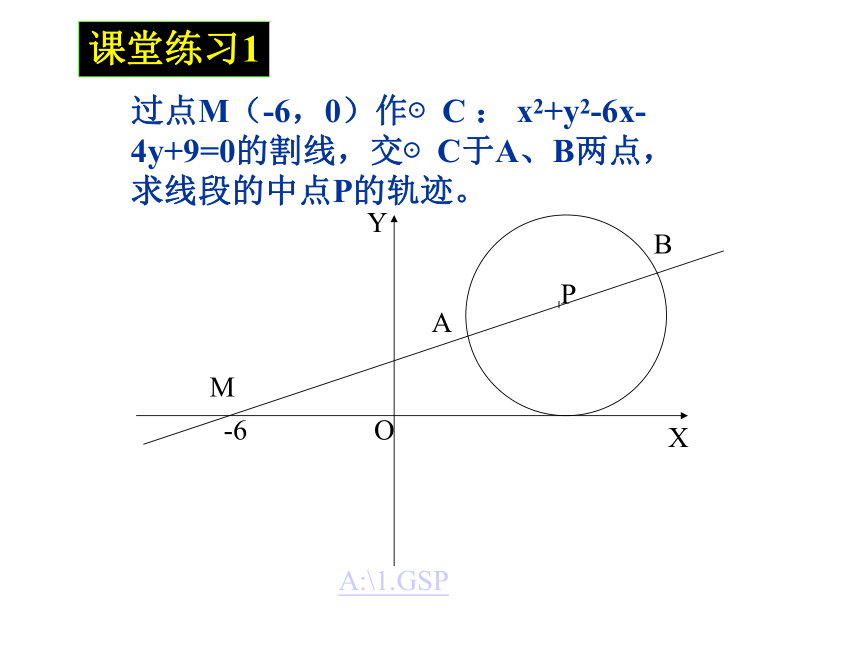
过点M(-6,0)作⊙C : x2+y2-6x-4y+9=0的割线,交⊙C于A、B两点,求线段的中点P的轨迹。
课堂练习1
2 . 定义法
当动点轨迹的条件符合某种基本轨迹的定义,我们可根据定义直接写出动点的轨迹方程。
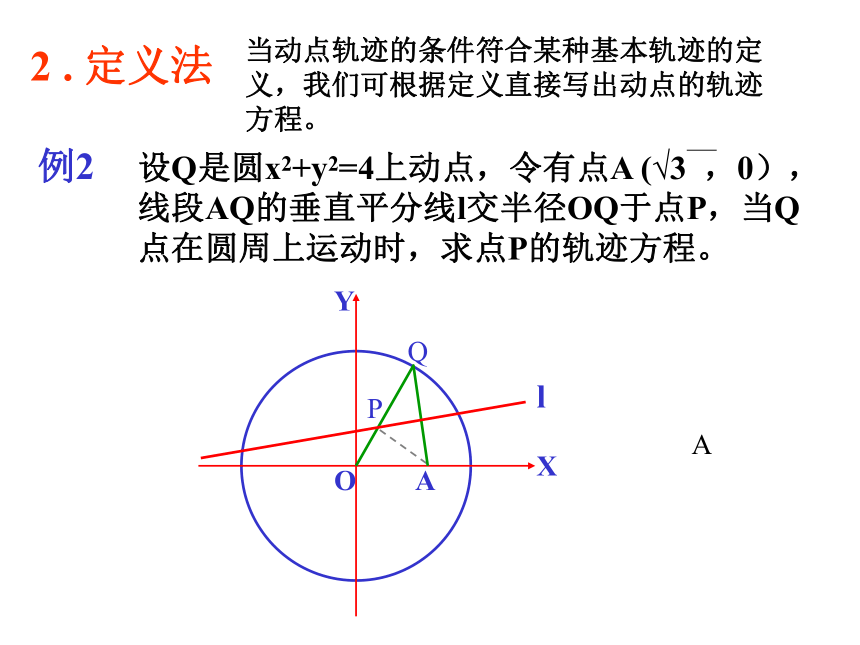
例2
A
O
X
Y
Q
P
l
A
设Q是圆x2+y2=4上动点,令有点A (√3 ,0),线段AQ的垂直平分线l交半径OQ于点P,当Q点在圆周上运动时,求点P的轨迹方程。
∵ P在AQ的垂直平分线上
∴ ∣PA︱=︱PQ︱
A
又P在半径OQ上
∴ ︱PO︱+︱PQ︱=2
∴ ︱PO︱+︱PA︱=2
且 2﹥
√3=|OA |
由椭圆的定义可知:P点的轨迹是以O、A为焦点的椭圆.
由2a=2, 2c= √3得 a=1 c= √3/2 故b2=1/4
故P点的轨迹方程为:
解:连结PA
O
X
Y
Q
P
l
A
(x- √3/2) 2+ =4
y2
1
4
A
课堂练习2
与两定圆⊙O : x2+y2 =1
⊙A:x2+y2-8x-33=0都相切的动圆圆心C的轨迹方程——————
X
Y
O
C
思路点拨
(1)寻求点C 满足的几何条件
(2)判定C的轨迹
(3)写出轨迹方程
(x-2)2 y2
9
5
=1
+
Key
3. 代换法(相关点法)
在一些问题中,动点P(x,y)随另一定点Q(x1,y1)(称之为相关点)而运动,如果相关点Q所满足的条件明显,或点Q在一已知曲线上运动,即满足f(x2,y2)=0①,这时 需求P,Q两点的坐标关系,如: x1=g(x,y) ,
y1= (x,y)
并将这一关系代入①式,即可以求得动点P的轨迹方程。
线段OA的一个端点O是原点,另一个端点A在 圆(x-a)2+y2=r2(a>0,r>0)上运动,以O为直角顶点作等腰直角三角形AOB。求顶点B轨方程。
例3
设法先求出相关点A的轨迹方程。
找出相关A与动点B间的坐标关系式。
消去相关点A的坐标。
分析:当动点B的变动是由另一个点A的变动引起时,可用“相关点法”,其中点A称为“相关点”,使用这一方法求轨迹方程的步骤是:
A
O
X
Y
B
C
A
O
X
Y
B
C
A:\2.GSP
解:
设,B(x , y )。过A,B分别作X轴的垂线,垂足分别是E,F。Rt△AOE ∽ Rt△OBF,OE=FB,EA=-OF,即有xo=y,y0=-x,代入圆C的方程,得到(y-a)2+x2=r2,这就是点B的轨迹方程,一个圆心在y轴正方向,半径仍然是r 的圆。
=
课堂练习3
《练习册》307页第6题
o
p
Q
C
小结:
1 求动点轨迹方程的实质就是
利用题设中的几何条件,通过“坐标化”将其转化为寻求变量x,y间关系的等式。
课外作业:
教材P112 见 4,5 ,6 ,7
2 求动点轨迹方程的三种常用方法与技巧.
L
O
X
Y
-3
-2
M
A
B
P
A:\3.GSP
过点M(-3,-2)作直线l,交椭圆 于A,B两点,求AB的中点P的轨迹方程。
X 2
2
+
y2
=1
课外练习
解:
设A( x1 ,y1 ), B( x2 ,y2 ), P( x ,y)
则有 kOPkAB=-1/2(a2=2,b2=1)。
因为kOP=y/x,kAB=(y+2)/(x+2)
所以y/x (y+2)/(x+2)=-1/2,即
X2+2y2+3x+4y=0。由{
X2+2y2+3x+4y=0
X2+2y2=2
解得x=
-6+4√15
17
-
所以得到所求的轨迹的方程是
X2+2y2+3x+4y=0, ( ≦x ≦
-6+4√15 )
17
-6-4√15
17
欢迎光临指导
课题的引入
一 平面解析几何研究的主要问题
由已知条件求曲线方程
通过曲线方程研究曲线的性质
二 求轨迹方程问题的类型
第一类 已知曲线形状
第二类 未知曲线形状
三 求轨迹方程的常见方法
直接法、定义法、代换法、
参数法、交轨法、复数法
【教学目标】
常用点的轨迹。
求动点的轨迹的常用方法与技巧.
通过对求轨迹方程的学习,培养学生综合运用各方面知识的能力.
【教学重点】
求动点的轨迹的常用方法与技巧.
【教学难点】
用代换法求动点的轨迹方法与技巧.
求曲线的轨迹方程(1)
复面解析几何研究的两大主要问题.
求曲线方程的一般步骤.
建系设点.
写出点集.
列方程.
化简方程.
检验方程.
二 求轨迹方程的常用方法
1.直接法
由题设所给(或通过分析图形的几何性质而得出)的动点所满足的几何条件列出等式,再用坐标代替这些等式,化简得曲线的方程,这种方法叫直接法。
x
y
o
k
例1
求和定圆x2+y2=k2的圆周的距离等于k的动点P的轨迹方程
P
解: 设动点P(x,y), 则有
︱OP︱ =2k或︱OP︱=0.
即 : x2+y2=4 k2或x2+y2=0
A:\1.GSP
B
M
X
Y
O
-6
A
P
过点M(-6,0)作⊙C : x2+y2-6x-4y+9=0的割线,交⊙C于A、B两点,求线段的中点P的轨迹。
课堂练习1
2 . 定义法
当动点轨迹的条件符合某种基本轨迹的定义,我们可根据定义直接写出动点的轨迹方程。
例2
A
O
X
Y
Q
P
l
A
设Q是圆x2+y2=4上动点,令有点A (√3 ,0),线段AQ的垂直平分线l交半径OQ于点P,当Q点在圆周上运动时,求点P的轨迹方程。
∵ P在AQ的垂直平分线上
∴ ∣PA︱=︱PQ︱
A
又P在半径OQ上
∴ ︱PO︱+︱PQ︱=2
∴ ︱PO︱+︱PA︱=2
且 2﹥
√3=|OA |
由椭圆的定义可知:P点的轨迹是以O、A为焦点的椭圆.
由2a=2, 2c= √3得 a=1 c= √3/2 故b2=1/4
故P点的轨迹方程为:
解:连结PA
O
X
Y
Q
P
l
A
(x- √3/2) 2+ =4
y2
1
4
A
课堂练习2
与两定圆⊙O : x2+y2 =1
⊙A:x2+y2-8x-33=0都相切的动圆圆心C的轨迹方程——————
X
Y
O
C
思路点拨
(1)寻求点C 满足的几何条件
(2)判定C的轨迹
(3)写出轨迹方程
(x-2)2 y2
9
5
=1
+
Key
3. 代换法(相关点法)
在一些问题中,动点P(x,y)随另一定点Q(x1,y1)(称之为相关点)而运动,如果相关点Q所满足的条件明显,或点Q在一已知曲线上运动,即满足f(x2,y2)=0①,这时 需求P,Q两点的坐标关系,如: x1=g(x,y) ,
y1= (x,y)
并将这一关系代入①式,即可以求得动点P的轨迹方程。
线段OA的一个端点O是原点,另一个端点A在 圆(x-a)2+y2=r2(a>0,r>0)上运动,以O为直角顶点作等腰直角三角形AOB。求顶点B轨方程。
例3
设法先求出相关点A的轨迹方程。
找出相关A与动点B间的坐标关系式。
消去相关点A的坐标。
分析:当动点B的变动是由另一个点A的变动引起时,可用“相关点法”,其中点A称为“相关点”,使用这一方法求轨迹方程的步骤是:
A
O
X
Y
B
C
A
O
X
Y
B
C
A:\2.GSP
解:
设,B(x , y )。过A,B分别作X轴的垂线,垂足分别是E,F。Rt△AOE ∽ Rt△OBF,OE=FB,EA=-OF,即有xo=y,y0=-x,代入圆C的方程,得到(y-a)2+x2=r2,这就是点B的轨迹方程,一个圆心在y轴正方向,半径仍然是r 的圆。
=
课堂练习3
《练习册》307页第6题
o
p
Q
C
小结:
1 求动点轨迹方程的实质就是
利用题设中的几何条件,通过“坐标化”将其转化为寻求变量x,y间关系的等式。
课外作业:
教材P112 见 4,5 ,6 ,7
2 求动点轨迹方程的三种常用方法与技巧.
L
O
X
Y
-3
-2
M
A
B
P
A:\3.GSP
过点M(-3,-2)作直线l,交椭圆 于A,B两点,求AB的中点P的轨迹方程。
X 2
2
+
y2
=1
课外练习
解:
设A( x1 ,y1 ), B( x2 ,y2 ), P( x ,y)
则有 kOPkAB=-1/2(a2=2,b2=1)。
因为kOP=y/x,kAB=(y+2)/(x+2)
所以y/x (y+2)/(x+2)=-1/2,即
X2+2y2+3x+4y=0。由{
X2+2y2+3x+4y=0
X2+2y2=2
解得x=
-6+4√15
17
-
所以得到所求的轨迹的方程是
X2+2y2+3x+4y=0, ( ≦x ≦
-6+4√15 )
17
-6-4√15
17
