人教版八年级数学上册15.3分式方程(第2课时)课件 (1)(共14张ppt)
文档属性
| 名称 | 人教版八年级数学上册15.3分式方程(第2课时)课件 (1)(共14张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 660.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 07:28:53 | ||
图片预览






文档简介
(共14张PPT)
15.3
分式方程
(第2课时)
前预习
1.如何解较复杂的分式方程和较简单的含有字母系
数的分式方程.
2.熟练掌握分式方程的一般步骤,体会转化的数学思想.
活动一
复习巩固解分式方程的步骤
1
解方程
解:方程两边同乘
,得
=3.
化简,得
=3.
解得
=1.
检验:当
=1时,
=0,
=1不是原分式
方程的解,所以,原分式方程无解.
2.解方程
解:方程两边同时乘以(x-2),得
(x-3)+(x-2)=-3
解得x=1
检验:当x=1时,x-2≠0
所以:原分式方程的解是x=1
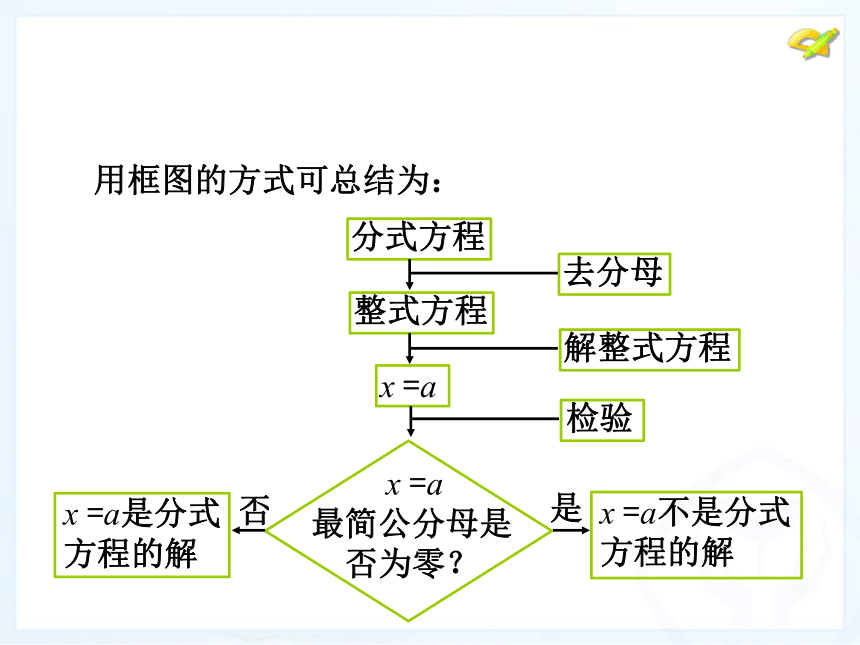
用框图的方式可总结为:
分式方程
整式方程
去分母
解整式方程
x
=a
检验
x
=a是分式
方程的解
x
=a不是分式
方程的解
x
=a
最简公分母是
否为零?
否
是
练一练
1 解方程:
解:方程两边同乘
,得
=
去括号,得
=
移项、合并同类项,得
=
∵
∴
1
解关于x
的方程
活动二
知识的延伸
∴
检验:当
时,x-a
0,
所以,
是原分式方程的解.
2.若分式
与1互为相反数,则x的值是______.
【解析】由题意得
=-1
∴-x+1=2
∴x=-1
当x=-1时,x-1≠0.
答案:-1
3.如果关于x的方程
无解,则m的值等于(
)
A.-3
B.-2
C.-1
D.3
【解析】选B.方程的两边都乘(x-3),得2=x-3-m,移项
并合并同类项得,x=5+m,由于方程无解,此时x=3,即5+m=3,
∴m=-2.
4.
关于x的方程
有增根,求k的值.
解:方程的两边同时乘(x+3)(x-3)得
x+3+kx-3k=k+3
整理得:(k+1)x=4k
因为方程无解,则x=3或x=-3
当x=3时,(k+1)
·3=4k,k=3,
当x=-3时,(k+1)(-3)=4k,
所以当k=3或
时,原分式方程无解.
解:方程两边同乘
,得
=0.
化简,得
=0.
移项、合并同类项,得
=
∵
0,
∴
0,
1 解关于x
的方程
活动三
课堂检测
∴
检验:当
时,
所以,
是原分式方程的解.
2
解方程
解方程
3.
如图,点A,B在数轴上,它们所对应的数分别
是-3和
且点A,B到原点的距离相等,求x的值.
解:依题意可知,
解得:
经检验,
是原方程的解.
则x的值为
(1)本节课学习了哪些主要内容?
(2)解分式方程的一般步骤有哪些?关键是什么?
解方程的过程中要注意的问题有哪些?
(3)列分式方程解应用题的步骤是什么?与列整式
方程解应用题的过程有什么区别和联系?
课堂小结
15.3
分式方程
(第2课时)
前预习
1.如何解较复杂的分式方程和较简单的含有字母系
数的分式方程.
2.熟练掌握分式方程的一般步骤,体会转化的数学思想.
活动一
复习巩固解分式方程的步骤
1
解方程
解:方程两边同乘
,得
=3.
化简,得
=3.
解得
=1.
检验:当
=1时,
=0,
=1不是原分式
方程的解,所以,原分式方程无解.
2.解方程
解:方程两边同时乘以(x-2),得
(x-3)+(x-2)=-3
解得x=1
检验:当x=1时,x-2≠0
所以:原分式方程的解是x=1
用框图的方式可总结为:
分式方程
整式方程
去分母
解整式方程
x
=a
检验
x
=a是分式
方程的解
x
=a不是分式
方程的解
x
=a
最简公分母是
否为零?
否
是
练一练
1 解方程:
解:方程两边同乘
,得
=
去括号,得
=
移项、合并同类项,得
=
∵
∴
1
解关于x
的方程
活动二
知识的延伸
∴
检验:当
时,x-a
0,
所以,
是原分式方程的解.
2.若分式
与1互为相反数,则x的值是______.
【解析】由题意得
=-1
∴-x+1=2
∴x=-1
当x=-1时,x-1≠0.
答案:-1
3.如果关于x的方程
无解,则m的值等于(
)
A.-3
B.-2
C.-1
D.3
【解析】选B.方程的两边都乘(x-3),得2=x-3-m,移项
并合并同类项得,x=5+m,由于方程无解,此时x=3,即5+m=3,
∴m=-2.
4.
关于x的方程
有增根,求k的值.
解:方程的两边同时乘(x+3)(x-3)得
x+3+kx-3k=k+3
整理得:(k+1)x=4k
因为方程无解,则x=3或x=-3
当x=3时,(k+1)
·3=4k,k=3,
当x=-3时,(k+1)(-3)=4k,
所以当k=3或
时,原分式方程无解.
解:方程两边同乘
,得
=0.
化简,得
=0.
移项、合并同类项,得
=
∵
0,
∴
0,
1 解关于x
的方程
活动三
课堂检测
∴
检验:当
时,
所以,
是原分式方程的解.
2
解方程
解方程
3.
如图,点A,B在数轴上,它们所对应的数分别
是-3和
且点A,B到原点的距离相等,求x的值.
解:依题意可知,
解得:
经检验,
是原方程的解.
则x的值为
(1)本节课学习了哪些主要内容?
(2)解分式方程的一般步骤有哪些?关键是什么?
解方程的过程中要注意的问题有哪些?
(3)列分式方程解应用题的步骤是什么?与列整式
方程解应用题的过程有什么区别和联系?
课堂小结
