【A典学案】冲刺100分 八年级上专题复习第四讲 一次函数课件(34张PPT)
文档属性
| 名称 | 【A典学案】冲刺100分 八年级上专题复习第四讲 一次函数课件(34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 15:03:12 | ||
图片预览








文档简介
第四讲 一次函数
北师大版 八年级上册
知识清单
1.函数
定义:一般地,在某个变化过程中,有两个变量 x 和 y,如果给定一个 x 值,相应地就__________了一个y 值,那么我们称__________是__________的函数,其中__________是自变量,__________是因变量.
表示方法:①__________;②__________;③__________.
画函数图像的步骤:__________、__________、__________.
2.一次函数
一次函数的一般形式为__________(k,b 为常数,k≠0).正比例函数的表
确定
y
x
x
y
列表法
图像法
解析式法
列表
描点
连线
y=kx+b
知识清单
达式为__________,正比例函数是一次函数中__________时的特殊情况.
3.一次函数的图象
一次函数 y=kx+b 的图象是一条直线,这条直线经过(0,___ ),画一次函数的图象只要确定满足表达式 y=kx+b 的_____个简单的点即可.
正比例函数 y=kx 的图象是一条经过(0,____)和(1,____)点的直线.
[注意]一次函数 y=kx+b 可由正比例函数 y=kx 平移得到,b>0,上移 b 个单位;b<0,下移|b|个单位.
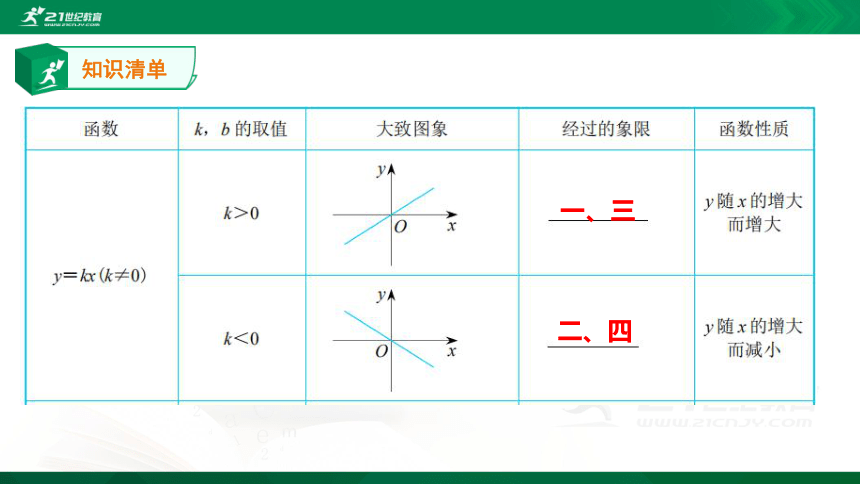
4.一次函数 y=kx+b 的性质
y=kx
b=0
b
2
0
k
知识清单
一、三
二、四
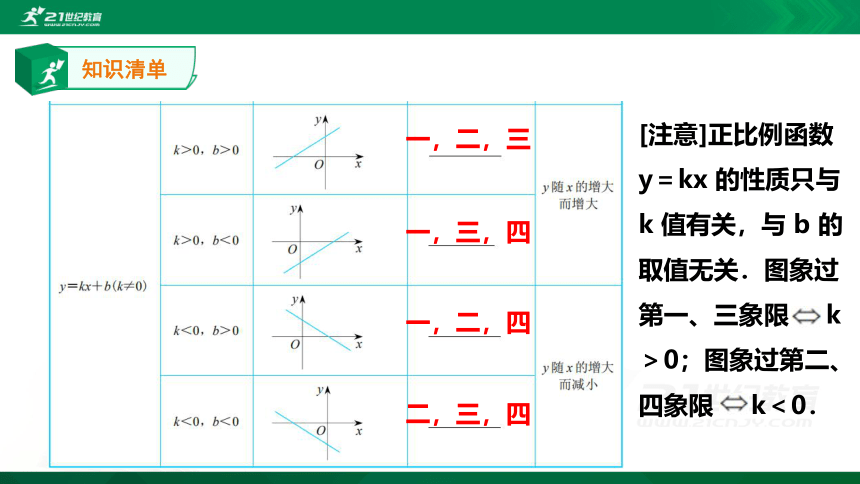
知识清单
一,二,三
一,三,四
一,二,四
二,三,四
[注意]正比例函数 y=kx 的性质只与 k 值有关,与 b 的取值无关.图象过第一、三象限 k>0;图象过第二、四象限 k<0.
知识清单
5.一次函数与一元一次方程
一次函数 y=kx+b(k,b 为常数,k≠0)的图象与 x 轴交点的______坐标的对应值即为一元一次方程 kx+b=0 的根.
6.用一次函数解决实际问题
(1)一次函数在现实生活中有着广泛的应用,在解答一次函数的应用题时,应从给定的信息中抽象出一次函数关系,理清哪个是自变量,哪个是自变量的函数,再利用一次函数的图象与性质求解,同时要注意自变量的取值范围.
横
知识清单
(2)一次函数 y=kx+b(k≠0)的自变量 x 的范围是全体实数.图象是直线,因此没有最大值与最小值.但由实际问题得到的一次函数解析式,自变量的取值范围一般受到限制,则图象为线段和射线,根据函数图象的性质,就存在最大值和最小值.
常见类型:(1)求一次函数的表达式;(2)利用一次函数的图象与性质解决某些问题如最值等.
典例精讲
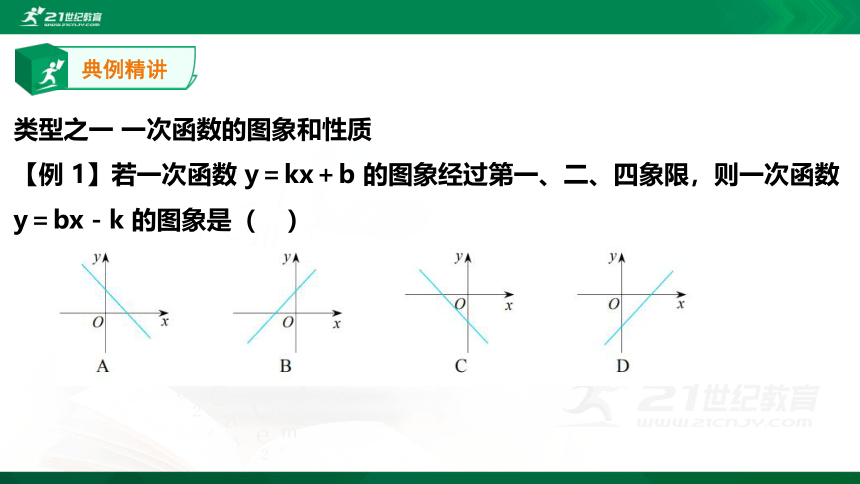
类型之一 一次函数的图象和性质
【例 1】若一次函数 y=kx+b 的图象经过第一、二、四象限,则一次函数 y=bx-k 的图象是( )
典例精讲
[解析]由一次函数 y=kx+b 的图象经过第一、二、四象限,可知 k<0,b>0,因此一次函数 y=bx-k 中一次项系数大于 0,常数项大于 0,即一次函数 y=bx-k 的图象经过第一、二、三象限.
故选 B.
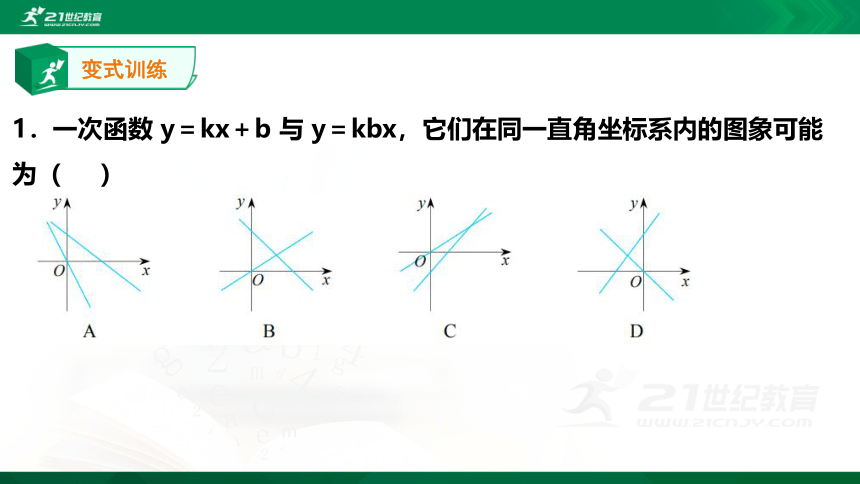
变式训练
1.一次函数 y=kx+b 与 y=kbx,它们在同一直角坐标系内的图象可能为( )
典例精讲
A 解析:由一次函数y=kx+b的图象可知k<0,b>0,∴kb<0,∴正比例函数y=kbx的图象应过第二、四象限,故本选项正确,B选项错误.
C项,由一次函数y=kx+b的图象可知k>0,b<0,∴kb<0,∴正比例函数y=kbx的图象应过第二、四象限,故本选项错误.
D项,由一次函数y=kx+b的图象可知k>0,b>0,∴kb>0,∴正比例函数y=kbx的图象应过第一、三象限,故本选项错误.
故选A.
典例精讲
类型之二 确定一次函数的表达式
【例 2】已知一个一次函数的图象经过 A(0,1),B(1,3)两点.
(1)求这个一次函数的表达式;
(2)试判断点 P(-1,1)是否在这个一次函数的图象上.
[解析](1)设这个一次函数的表达式为 y=kx+b(k≠0).
∵函数图象过点 A(0,1),∴b=1.
将 B(1,3)代入 y=kx+1 中,得 3=k+1,解得 k=2.
∴这个一次函数的表达式为 y=2x+1.
典例精讲
(2)当 x=-1 时,y=2×(-1)+1=-1≠1,
∴点 P 不在这个一次函数的图象上.
变式训练
2.设一次函数 y=kx+b 的图象经过点 A(2,-1)和点 B,其中点 B 是直线 y=-2x+1 与 y 轴的交点,求这个函数的表达式.
解析:∵直线y=-2x+1与y轴的交点坐标为(0,1),则点(0,1)也在直线y=kx+b上,
∴b=1.
把b=1和点(2,-1)代入y=kx+b,得-1=2k+1,解得k=-1.
∴这个函数的表达式为y=-x+1.
典例精讲
类型之三 数形结合思想
【例 3】如图,在△ABC 中,∠ACB=90°,AC= ,斜边 AB 在 x 轴上,点 C 在 y 轴的正半轴上,点 A 的坐标为(2,0).则直角边 BC 所在直线的表达式为_______.
典例精讲
[解析]点 A 的坐标为(2,0),则 OA=2,
在△ABC 中,∠ACB=90°, ,OC⊥AB 于点 O,
则由勾股定理可得 OC=4,即点 C 的坐标为(0,4).
设 OB=x,则 AB=2+x. 在 Rt△BOC 中,
在 Rt△ABC 中,
,解得 x=8.
∴点 B 的坐标是(-8,0),
∴直线 BC 的表达式为 .故答案为:
变式训练
3.一次函数 y=(3-a)x+b-2 在直角坐标系中的图象如图,化简:
=________.
解析:根据图象可知直线y=(3-a)x+b-2经过第二、三、四象限,
∴3-a<0,b-2<0.
故答案为:a+b-5.
典例精讲
类型之四 一次函数的应用
【例 4】A,B 两地相距 1100 米,甲从 A 地出发,乙从 B 地出发,相向而行,甲比乙先出发 2 分钟,乙出发 7 分钟后与甲相遇.设甲、乙两人相距 y 米,甲行进的时间为 t 分钟,y 与 t 之间的函数关系如图所示.请你结合图象探究:
(1)甲的行进速度为每分钟_________米,m=_________;
(2)求直线 PQ 对应的函数表达式;
(3)求乙的行进速度.
典例精讲
[解析](1)60;9.
(2)设 PQ 所在直线的表达式为 y=kt+b(k≠0).
∵点 P(0,1100)在直线 PQ 上,
∴b=1100,PQ 所在直线的表达式为 y=kt+1100.
又∵点 Q(2,980)也在直线 PQ 上,
∴将 Q(2,980)代入 y=kt+1100,得 980=2k+1100,解得 k=-60,
∴直线 PQ 对应的函数表达式为 y=-60t+1100.
(3)设乙的行进速度为 x 米/分.由题意,得 60×9+7x=1100,解得 x=80.答:乙的行进速度为 80 米/分.
变式训练
4.甲、乙两人进行赛跑,甲比乙跑得快,现在甲让乙先跑 10 m,甲再起跑.图中的 和 分别表示甲、乙两人跑步的路程 y(m)与甲跑步的时间 x(s)之间的函数关系,其中 对应的函数表达式为 ,则甲追上乙用了多长时间?
变式训练
解:设 =kx+b(k≠0).
由函数图象知b=10.
将(2,22)代入 =kx+10,得22=2k+10.解得k=6.
∴ =6x+10.
当 时,8x=6x+10,解这个方程,得x=5.
答:甲追上乙用了5 s
区校真题
1.(深中)若一个正比例函数的图象经过 A(3,6),B(m,4)两点,则 m 的值为( )
A.2 B.8 C.-2 D.-8
2.(龙岗)一次函数 y=kx+b 满足 kb<0,且 y 随 x 的增大而减小,则此函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
A
C
区校真题
3.(福田)如图,一次函数 y=kx+b 的图象经过点(2,0),则下列结论正确的是( )
A.k>0 B.关于 x 方程 kx+b=0 的解是 x=2
C.b<0 D.y 随 x 的增大而增大
4.(深实验)已知一次函数 y=kx+b 的图象经过点(-2,3),且 y 的值随 x 值的增大而增大,则下列判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
B
A
区校真题
5.(宝安)为了鼓励居民节约用水,某市决定实行两级收费制度,水费 y(元)与用水量 x(吨)之间的函数关系如图所示.若每月用水量不超过 20 吨(含 20 吨),按政府优惠价收费;若每月用水量超过 20吨,超过部分按市场价 3.5 元/吨收费,那么政府优惠价是( )
A.2 元/吨 B.2.2 元/吨 C.2.3 元/吨 D.2.5 元/吨
C
区校真题
6.(深外)若函数 y=(k-1)x+2 是关于 x 的一次函数,且 y 的值随 x 值的增大而减小,则 k 的取值范围是___________.
7.(龙岗)如图,函数 y=2x+b 与函数 y=kx-1 的图象交于点 P,则关于 x 的方程 kx-1=2x+b 的解是_____________.
k<1
x=1
区校真题
8.(深外)如图,直线 y=kx+3 与 x 轴、y 轴分别相交于 E,F 两点.点 E 的坐标为(-6,0),点 P 是直线 EF 上的一点.
(1)求 k 的值;
(2)若△POE 的面积为 6,求点 P 的坐标.
区校真题
解:(1)把E的坐标为(-6,0)代入直线y=kx+3,得-6k+3=0,解得k=
(2)设P(x,y),
∴|y|=2,即y=2,或y=-2.
当y=2时,即 ,解得x=-2,∴P(-2,2).
当y=-2时,即 ,解得x=-10,∴P(-10,-2).
∴点P的坐标为(-2,2)或(-10,-2).
区校真题
9.(罗湖)小明从深圳往广州邮寄一件包裹,邮资收费标准为每干克 0.9 元,并每件另加收手续费 3.5 元.
(1)求总邮资 y(元)与包裹重量 x(干克)之间的函数关系式;
(2)若小明的包裹重量为 5 千克,则小明应付的总邮资为多少?
(3)若小明所付总邮资为 12.5 元,则小明的包裹重量为多少?
区校真题
解析:(1)依题意,得y=0.9x+3.5.
(2)把x=5代入y=0.9x+3.5,得y=0.9×5+3.5=8(元)
答:若小明的包裹重量为5千克,则小明应付的总邮资为8元.
(3)把y=12.5代入y=0.9x+3.5,得12.5=0.9x+3.5,解得x=10.
答:若小明所付总邮资为12.5元,则小明的包裹重量为10千克.
中考链接
1.已知一次函数 =ax+b 和 =bx+a(a≠b),函数 和 的图象可能是( )
A
中考链接
2.某生态体验园推出了甲、乙两种消费卡,设入园次数为 x 时所需费用为 y 元,选择这两种卡消费时,y 与 x 的函数关系如图所示,解答下列问题:
(1)分别求出选择这两种卡消费时,y 关于 x 的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
中考链接
(1)设 ,根据题意,得 ,解得 ,
设 ,根据题意,得 ,解得 ,
(2)① ,即20x<10x+100,解得x<10,当入园次数小于10次时,选择甲消费卡比较合算;
② ,即20x=10x+100,解得x=10,当入园次数等于10次时,选择两种消费卡费用一样;
③ ,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版 八年级上册
知识清单
1.函数
定义:一般地,在某个变化过程中,有两个变量 x 和 y,如果给定一个 x 值,相应地就__________了一个y 值,那么我们称__________是__________的函数,其中__________是自变量,__________是因变量.
表示方法:①__________;②__________;③__________.
画函数图像的步骤:__________、__________、__________.
2.一次函数
一次函数的一般形式为__________(k,b 为常数,k≠0).正比例函数的表
确定
y
x
x
y
列表法
图像法
解析式法
列表
描点
连线
y=kx+b
知识清单
达式为__________,正比例函数是一次函数中__________时的特殊情况.
3.一次函数的图象
一次函数 y=kx+b 的图象是一条直线,这条直线经过(0,___ ),画一次函数的图象只要确定满足表达式 y=kx+b 的_____个简单的点即可.
正比例函数 y=kx 的图象是一条经过(0,____)和(1,____)点的直线.
[注意]一次函数 y=kx+b 可由正比例函数 y=kx 平移得到,b>0,上移 b 个单位;b<0,下移|b|个单位.
4.一次函数 y=kx+b 的性质
y=kx
b=0
b
2
0
k
知识清单
一、三
二、四
知识清单
一,二,三
一,三,四
一,二,四
二,三,四
[注意]正比例函数 y=kx 的性质只与 k 值有关,与 b 的取值无关.图象过第一、三象限 k>0;图象过第二、四象限 k<0.
知识清单
5.一次函数与一元一次方程
一次函数 y=kx+b(k,b 为常数,k≠0)的图象与 x 轴交点的______坐标的对应值即为一元一次方程 kx+b=0 的根.
6.用一次函数解决实际问题
(1)一次函数在现实生活中有着广泛的应用,在解答一次函数的应用题时,应从给定的信息中抽象出一次函数关系,理清哪个是自变量,哪个是自变量的函数,再利用一次函数的图象与性质求解,同时要注意自变量的取值范围.
横
知识清单
(2)一次函数 y=kx+b(k≠0)的自变量 x 的范围是全体实数.图象是直线,因此没有最大值与最小值.但由实际问题得到的一次函数解析式,自变量的取值范围一般受到限制,则图象为线段和射线,根据函数图象的性质,就存在最大值和最小值.
常见类型:(1)求一次函数的表达式;(2)利用一次函数的图象与性质解决某些问题如最值等.
典例精讲
类型之一 一次函数的图象和性质
【例 1】若一次函数 y=kx+b 的图象经过第一、二、四象限,则一次函数 y=bx-k 的图象是( )
典例精讲
[解析]由一次函数 y=kx+b 的图象经过第一、二、四象限,可知 k<0,b>0,因此一次函数 y=bx-k 中一次项系数大于 0,常数项大于 0,即一次函数 y=bx-k 的图象经过第一、二、三象限.
故选 B.
变式训练
1.一次函数 y=kx+b 与 y=kbx,它们在同一直角坐标系内的图象可能为( )
典例精讲
A 解析:由一次函数y=kx+b的图象可知k<0,b>0,∴kb<0,∴正比例函数y=kbx的图象应过第二、四象限,故本选项正确,B选项错误.
C项,由一次函数y=kx+b的图象可知k>0,b<0,∴kb<0,∴正比例函数y=kbx的图象应过第二、四象限,故本选项错误.
D项,由一次函数y=kx+b的图象可知k>0,b>0,∴kb>0,∴正比例函数y=kbx的图象应过第一、三象限,故本选项错误.
故选A.
典例精讲
类型之二 确定一次函数的表达式
【例 2】已知一个一次函数的图象经过 A(0,1),B(1,3)两点.
(1)求这个一次函数的表达式;
(2)试判断点 P(-1,1)是否在这个一次函数的图象上.
[解析](1)设这个一次函数的表达式为 y=kx+b(k≠0).
∵函数图象过点 A(0,1),∴b=1.
将 B(1,3)代入 y=kx+1 中,得 3=k+1,解得 k=2.
∴这个一次函数的表达式为 y=2x+1.
典例精讲
(2)当 x=-1 时,y=2×(-1)+1=-1≠1,
∴点 P 不在这个一次函数的图象上.
变式训练
2.设一次函数 y=kx+b 的图象经过点 A(2,-1)和点 B,其中点 B 是直线 y=-2x+1 与 y 轴的交点,求这个函数的表达式.
解析:∵直线y=-2x+1与y轴的交点坐标为(0,1),则点(0,1)也在直线y=kx+b上,
∴b=1.
把b=1和点(2,-1)代入y=kx+b,得-1=2k+1,解得k=-1.
∴这个函数的表达式为y=-x+1.
典例精讲
类型之三 数形结合思想
【例 3】如图,在△ABC 中,∠ACB=90°,AC= ,斜边 AB 在 x 轴上,点 C 在 y 轴的正半轴上,点 A 的坐标为(2,0).则直角边 BC 所在直线的表达式为_______.
典例精讲
[解析]点 A 的坐标为(2,0),则 OA=2,
在△ABC 中,∠ACB=90°, ,OC⊥AB 于点 O,
则由勾股定理可得 OC=4,即点 C 的坐标为(0,4).
设 OB=x,则 AB=2+x. 在 Rt△BOC 中,
在 Rt△ABC 中,
,解得 x=8.
∴点 B 的坐标是(-8,0),
∴直线 BC 的表达式为 .故答案为:
变式训练
3.一次函数 y=(3-a)x+b-2 在直角坐标系中的图象如图,化简:
=________.
解析:根据图象可知直线y=(3-a)x+b-2经过第二、三、四象限,
∴3-a<0,b-2<0.
故答案为:a+b-5.
典例精讲
类型之四 一次函数的应用
【例 4】A,B 两地相距 1100 米,甲从 A 地出发,乙从 B 地出发,相向而行,甲比乙先出发 2 分钟,乙出发 7 分钟后与甲相遇.设甲、乙两人相距 y 米,甲行进的时间为 t 分钟,y 与 t 之间的函数关系如图所示.请你结合图象探究:
(1)甲的行进速度为每分钟_________米,m=_________;
(2)求直线 PQ 对应的函数表达式;
(3)求乙的行进速度.
典例精讲
[解析](1)60;9.
(2)设 PQ 所在直线的表达式为 y=kt+b(k≠0).
∵点 P(0,1100)在直线 PQ 上,
∴b=1100,PQ 所在直线的表达式为 y=kt+1100.
又∵点 Q(2,980)也在直线 PQ 上,
∴将 Q(2,980)代入 y=kt+1100,得 980=2k+1100,解得 k=-60,
∴直线 PQ 对应的函数表达式为 y=-60t+1100.
(3)设乙的行进速度为 x 米/分.由题意,得 60×9+7x=1100,解得 x=80.答:乙的行进速度为 80 米/分.
变式训练
4.甲、乙两人进行赛跑,甲比乙跑得快,现在甲让乙先跑 10 m,甲再起跑.图中的 和 分别表示甲、乙两人跑步的路程 y(m)与甲跑步的时间 x(s)之间的函数关系,其中 对应的函数表达式为 ,则甲追上乙用了多长时间?
变式训练
解:设 =kx+b(k≠0).
由函数图象知b=10.
将(2,22)代入 =kx+10,得22=2k+10.解得k=6.
∴ =6x+10.
当 时,8x=6x+10,解这个方程,得x=5.
答:甲追上乙用了5 s
区校真题
1.(深中)若一个正比例函数的图象经过 A(3,6),B(m,4)两点,则 m 的值为( )
A.2 B.8 C.-2 D.-8
2.(龙岗)一次函数 y=kx+b 满足 kb<0,且 y 随 x 的增大而减小,则此函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
A
C
区校真题
3.(福田)如图,一次函数 y=kx+b 的图象经过点(2,0),则下列结论正确的是( )
A.k>0 B.关于 x 方程 kx+b=0 的解是 x=2
C.b<0 D.y 随 x 的增大而增大
4.(深实验)已知一次函数 y=kx+b 的图象经过点(-2,3),且 y 的值随 x 值的增大而增大,则下列判断正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
B
A
区校真题
5.(宝安)为了鼓励居民节约用水,某市决定实行两级收费制度,水费 y(元)与用水量 x(吨)之间的函数关系如图所示.若每月用水量不超过 20 吨(含 20 吨),按政府优惠价收费;若每月用水量超过 20吨,超过部分按市场价 3.5 元/吨收费,那么政府优惠价是( )
A.2 元/吨 B.2.2 元/吨 C.2.3 元/吨 D.2.5 元/吨
C
区校真题
6.(深外)若函数 y=(k-1)x+2 是关于 x 的一次函数,且 y 的值随 x 值的增大而减小,则 k 的取值范围是___________.
7.(龙岗)如图,函数 y=2x+b 与函数 y=kx-1 的图象交于点 P,则关于 x 的方程 kx-1=2x+b 的解是_____________.
k<1
x=1
区校真题
8.(深外)如图,直线 y=kx+3 与 x 轴、y 轴分别相交于 E,F 两点.点 E 的坐标为(-6,0),点 P 是直线 EF 上的一点.
(1)求 k 的值;
(2)若△POE 的面积为 6,求点 P 的坐标.
区校真题
解:(1)把E的坐标为(-6,0)代入直线y=kx+3,得-6k+3=0,解得k=
(2)设P(x,y),
∴|y|=2,即y=2,或y=-2.
当y=2时,即 ,解得x=-2,∴P(-2,2).
当y=-2时,即 ,解得x=-10,∴P(-10,-2).
∴点P的坐标为(-2,2)或(-10,-2).
区校真题
9.(罗湖)小明从深圳往广州邮寄一件包裹,邮资收费标准为每干克 0.9 元,并每件另加收手续费 3.5 元.
(1)求总邮资 y(元)与包裹重量 x(干克)之间的函数关系式;
(2)若小明的包裹重量为 5 千克,则小明应付的总邮资为多少?
(3)若小明所付总邮资为 12.5 元,则小明的包裹重量为多少?
区校真题
解析:(1)依题意,得y=0.9x+3.5.
(2)把x=5代入y=0.9x+3.5,得y=0.9×5+3.5=8(元)
答:若小明的包裹重量为5千克,则小明应付的总邮资为8元.
(3)把y=12.5代入y=0.9x+3.5,得12.5=0.9x+3.5,解得x=10.
答:若小明所付总邮资为12.5元,则小明的包裹重量为10千克.
中考链接
1.已知一次函数 =ax+b 和 =bx+a(a≠b),函数 和 的图象可能是( )
A
中考链接
2.某生态体验园推出了甲、乙两种消费卡,设入园次数为 x 时所需费用为 y 元,选择这两种卡消费时,y 与 x 的函数关系如图所示,解答下列问题:
(1)分别求出选择这两种卡消费时,y 关于 x 的函数表达式;
(2)请根据入园次数确定选择哪种卡消费比较合算.
中考链接
(1)设 ,根据题意,得 ,解得 ,
设 ,根据题意,得 ,解得 ,
(2)① ,即20x<10x+100,解得x<10,当入园次数小于10次时,选择甲消费卡比较合算;
② ,即20x=10x+100,解得x=10,当入园次数等于10次时,选择两种消费卡费用一样;
③ ,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
