人教版数学八年级上册13.1.2线段的垂直平分线的性质 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.1.2线段的垂直平分线的性质 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
13.1.2线段的垂直平分线的性质(一)
学习目标:
1、掌握线段垂直平分线的性质定理及其逆定理的证明和应用。
2、经历用尺规作线段垂直平分线的过程,培养动手操作的能力。
3、培养步步有据的推理意识。
学习重、难点:
线段垂直平分线的性质定理及其逆定理的灵活运用。
线段的垂直平分线定义:
定义:经过线段中点并且垂直于这条线段的直线称为这条线段的垂直平分线,又叫线段的中垂线。
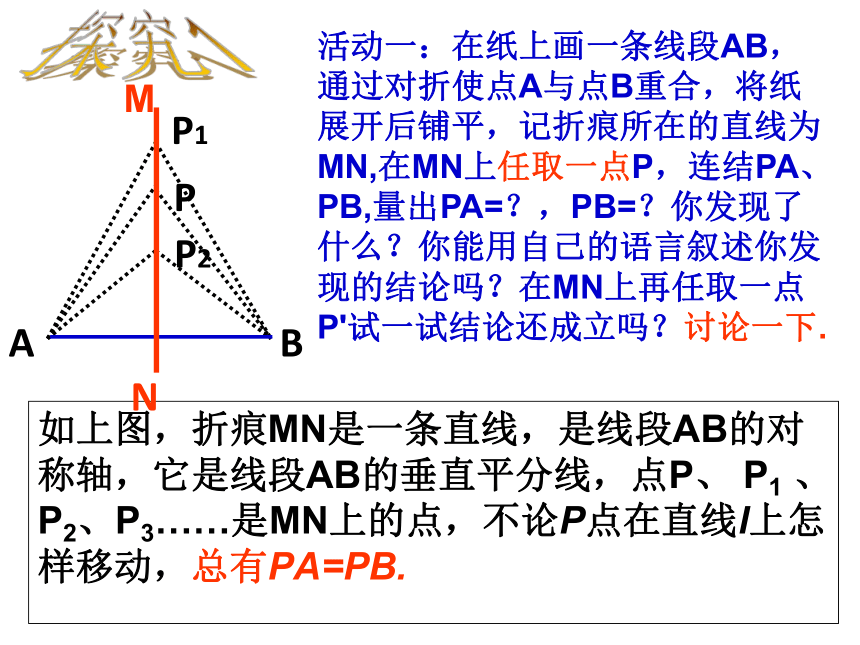
如上图,折痕MN是一条直线,是线段AB的对称轴,它是线段AB的垂直平分线,点P、
P1
、P2、P3……是MN上的点,不论P点在直线l上怎样移动,总有PA=PB.
探究1
P2
N
A
B
P
P1
M
活动一:在纸上画一条线段AB,通过对折使点A与点B重合,将纸展开后铺平,记折痕所在的直线为MN,在MN上任取一点P,连结PA、PB,量出PA=?,PB=?你发现了什么?你能用自己的语言叙述你发现的结论吗?在MN上再任取一点P'试一试结论还成立吗?讨论一下.
猜
想
P
A
B
C
l
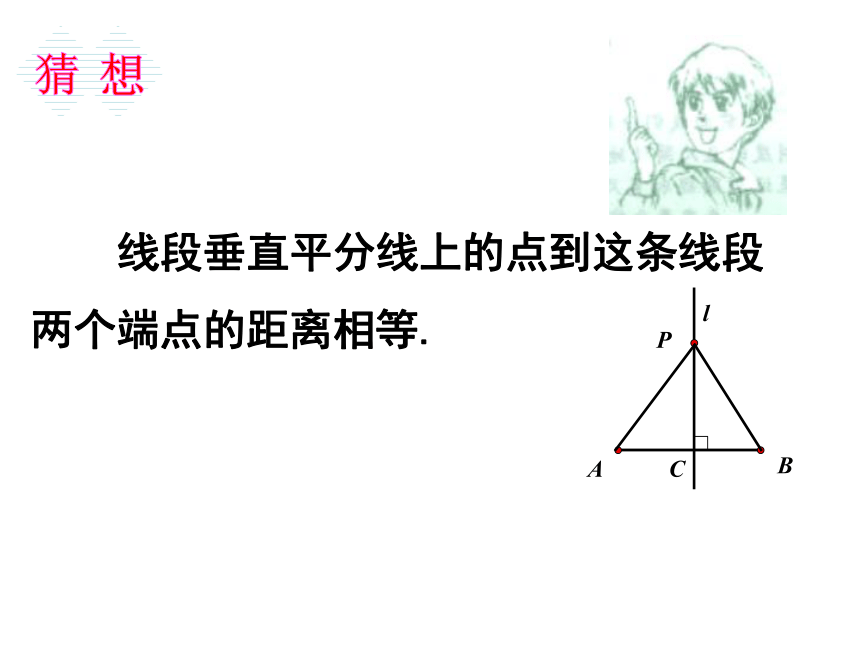
线段垂直平分线上的点到这条线段
两个端点的距离相等.
A
C
B
P
M
N
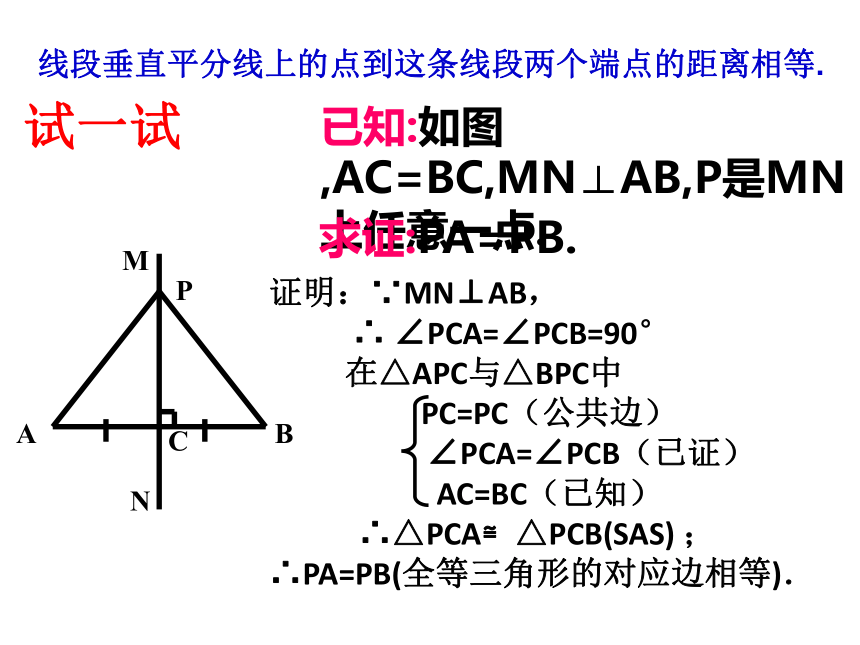
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
证明:∵MN⊥AB,
∴
∠PCA=∠PCB=90°
在△APC与△BPC中
PC=PC(公共边)
∠PCA=∠PCB(已证)
AC=BC(已知)
∴△PCA≌△PCB(SAS)
;
∴PA=PB(全等三角形的对应边相等).
求证:PA=PB.
试一试
线段垂直平分线上的点到这条线段两个端点的距离相等.
得出结论
文字表达:
线段的垂直平分线上的点到这条线段的两个端点的距离相等.
符号表达(即格式):
线段垂直平分线的性质定理:
∵AC=BC,MN⊥AB,P是MN上任意一点∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
1、(定义)经过线段中点并且垂直于这条线段的直线称为这条线段的垂直平分线,又叫这条线段的中垂线。
2、(性质)线段的垂直平分线上的点到这条线段两个端点的距离相等。
识
记
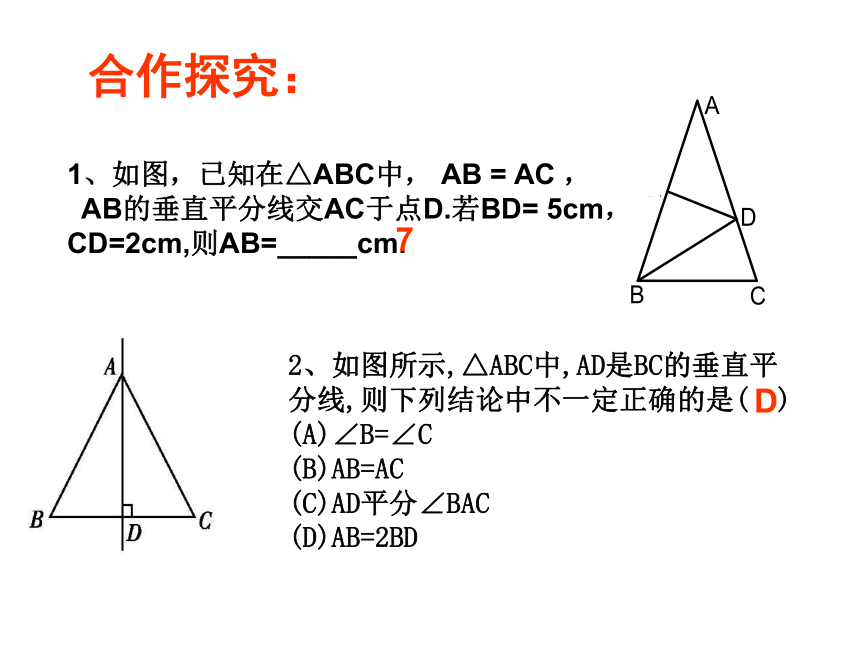
2、如图所示,△ABC中,AD是BC的垂直平分线,则下列结论中不一定正确的是( )
(A)∠B=∠C
(B)AB=AC
(C)AD平分∠BAC
(D)AB=2BD
D
1、如图,已知在△ABC中,
AB
=
AC
,
AB的垂直平分线交AC于点D.若BD=
5cm,CD=2cm,则AB=_____cm.
7
合作探究:
3、如图所示,在△ABC中,ABcm,△ABE的周长是24
cm,求AB的长.
解:∵DE是线段BC的垂直平分线,
∴BE=CE,
又∵AB+AE+BE=24(cm),
∴AB+AE+CE=24
(cm).
∵AE+CE=AC=15
(cm),
∴AB=24-15=9
(cm).
∴AB的长为9
cm.
合作探究:
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
已知:PA=PB
求证:点P在线段AB的垂直平分线上
证明:作PC⊥AB,垂足为C
∴∠ACP=∠BCP=900
在Rt△ACP和Rt△BCP中
∴
Rt△ACP≌Rt△BCP(HL)
∴AC=BC
又∵
PC⊥AB
∴点P在线段AB的垂直平分线上
探究2
P
A
B
C
有没有其它的证明思路?
文字表达:与一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
符号表达(即格式)
:
∵PA=PB
∴点P在线段AB的垂直平分线上
得出结论
到线段的两个端点距离相等的点有几个呢?
性质定理:在线段垂直平分线上的点到线段两个端点距离都相等。
逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上。
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
辨析:
4、如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
答:直线AM是线段BC的垂直平分线
理由:∵AB=AC
∴点A在线段BC的垂直平分线上
同理:点M在线段BC的垂直平分线上
∴直线AM是线段BC的垂直平分线
合作探究:
在纸上画线段AB,再分别用下列不同的工具画出线段的垂直平分线.
(1)用两把完全相同且不带刻度的直尺;
(2)用带刻度的直角三角板.
做一做
A
B
A
B
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
知识点:
1、到一条线段两个端点距离相等的点,在这条线段的
垂直平分线上.
2、两点确定一条直线.
分
析
请你用圆规和直尺亲自操作(尺规作图)
思考:有没有更准确的作线段AB的垂直平分线的
方法呢?
基本作图:
作线段的垂直平分线。
已知:线段AB,
求作:线段AB的垂直平分线。
A
B
C
D
作法:
(2)作直线CD。
直线CD即为所求。
(1)分别以点A、B为圆心,以大于——AB的长为半径作弧,两弧交于C、D两点;
1
2
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴。
5、有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
提示:连接AB、BC、CA,作三角形任意两边的垂直平分线,其交点即为所求。
小试牛刀:
1.已知线段AB和它外一点P,若PA=PB,则点P在
AB的 ;
若点P在AB的 ,则PA=PB.?
高
速
公
路
A
B
在某高速公路l的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么?
生活中的数学
l
能想通为什么吗?
作法:
1、连接AB。
2、作线段AB的垂直平分线
交直线l于点P
则点P为所求的水厂的位置
P
3.如图所示,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在(
)
(A)在AC、BC两边高线的交点处
(B)在AC、BC两边中线的交点处
(C)在AC、BC两边垂直平分线的交点处
(D)在A、B两内角平分线的交点处
解:∵DE垂直平分BC,
∴DB=DC.
∵AC+AD+DC=14
cm,
∴AC+AD+BD=14
cm,
即AC+AB=14
cm.
设AB=x
cm,AC=y
cm.
根据题意,得
解得
答:AB长为8
cm,AC长为6
cm.
4、如图所示,已知AB比AC长2
cm,BC的垂直平分线交AB于D,交BC于点E,
△ACD的周长是14
cm,求AB和AC的长.(学案:课时自测
第4题)
求证:
三角形三边垂直平分线交于一点,且这一点到三角形三个顶点的距离相等。
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理
PB=PC.
∴PA=PC.
∴点P也在边AC的垂直平分线上,且PA=PB=PC
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P也在边AC的垂直平分线上,且PA=PB=PC.
B
A
C
M
N
M’
N’
P
课堂小结
1.本节课学习了哪些知识?
2.通过本节课的学习,你又掌握了哪些
学习方法?
再
见
13.1.2线段的垂直平分线的性质(一)
学习目标:
1、掌握线段垂直平分线的性质定理及其逆定理的证明和应用。
2、经历用尺规作线段垂直平分线的过程,培养动手操作的能力。
3、培养步步有据的推理意识。
学习重、难点:
线段垂直平分线的性质定理及其逆定理的灵活运用。
线段的垂直平分线定义:
定义:经过线段中点并且垂直于这条线段的直线称为这条线段的垂直平分线,又叫线段的中垂线。
如上图,折痕MN是一条直线,是线段AB的对称轴,它是线段AB的垂直平分线,点P、
P1
、P2、P3……是MN上的点,不论P点在直线l上怎样移动,总有PA=PB.
探究1
P2
N
A
B
P
P1
M
活动一:在纸上画一条线段AB,通过对折使点A与点B重合,将纸展开后铺平,记折痕所在的直线为MN,在MN上任取一点P,连结PA、PB,量出PA=?,PB=?你发现了什么?你能用自己的语言叙述你发现的结论吗?在MN上再任取一点P'试一试结论还成立吗?讨论一下.
猜
想
P
A
B
C
l
线段垂直平分线上的点到这条线段
两个端点的距离相等.
A
C
B
P
M
N
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
证明:∵MN⊥AB,
∴
∠PCA=∠PCB=90°
在△APC与△BPC中
PC=PC(公共边)
∠PCA=∠PCB(已证)
AC=BC(已知)
∴△PCA≌△PCB(SAS)
;
∴PA=PB(全等三角形的对应边相等).
求证:PA=PB.
试一试
线段垂直平分线上的点到这条线段两个端点的距离相等.
得出结论
文字表达:
线段的垂直平分线上的点到这条线段的两个端点的距离相等.
符号表达(即格式):
线段垂直平分线的性质定理:
∵AC=BC,MN⊥AB,P是MN上任意一点∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
1、(定义)经过线段中点并且垂直于这条线段的直线称为这条线段的垂直平分线,又叫这条线段的中垂线。
2、(性质)线段的垂直平分线上的点到这条线段两个端点的距离相等。
识
记
2、如图所示,△ABC中,AD是BC的垂直平分线,则下列结论中不一定正确的是( )
(A)∠B=∠C
(B)AB=AC
(C)AD平分∠BAC
(D)AB=2BD
D
1、如图,已知在△ABC中,
AB
=
AC
,
AB的垂直平分线交AC于点D.若BD=
5cm,CD=2cm,则AB=_____cm.
7
合作探究:
3、如图所示,在△ABC中,AB
cm,求AB的长.
解:∵DE是线段BC的垂直平分线,
∴BE=CE,
又∵AB+AE+BE=24(cm),
∴AB+AE+CE=24
(cm).
∵AE+CE=AC=15
(cm),
∴AB=24-15=9
(cm).
∴AB的长为9
cm.
合作探究:
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
已知:PA=PB
求证:点P在线段AB的垂直平分线上
证明:作PC⊥AB,垂足为C
∴∠ACP=∠BCP=900
在Rt△ACP和Rt△BCP中
∴
Rt△ACP≌Rt△BCP(HL)
∴AC=BC
又∵
PC⊥AB
∴点P在线段AB的垂直平分线上
探究2
P
A
B
C
有没有其它的证明思路?
文字表达:与一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
符号表达(即格式)
:
∵PA=PB
∴点P在线段AB的垂直平分线上
得出结论
到线段的两个端点距离相等的点有几个呢?
性质定理:在线段垂直平分线上的点到线段两个端点距离都相等。
逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上。
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
辨析:
4、如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
答:直线AM是线段BC的垂直平分线
理由:∵AB=AC
∴点A在线段BC的垂直平分线上
同理:点M在线段BC的垂直平分线上
∴直线AM是线段BC的垂直平分线
合作探究:
在纸上画线段AB,再分别用下列不同的工具画出线段的垂直平分线.
(1)用两把完全相同且不带刻度的直尺;
(2)用带刻度的直角三角板.
做一做
A
B
A
B
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
知识点:
1、到一条线段两个端点距离相等的点,在这条线段的
垂直平分线上.
2、两点确定一条直线.
分
析
请你用圆规和直尺亲自操作(尺规作图)
思考:有没有更准确的作线段AB的垂直平分线的
方法呢?
基本作图:
作线段的垂直平分线。
已知:线段AB,
求作:线段AB的垂直平分线。
A
B
C
D
作法:
(2)作直线CD。
直线CD即为所求。
(1)分别以点A、B为圆心,以大于——AB的长为半径作弧,两弧交于C、D两点;
1
2
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴。
5、有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
提示:连接AB、BC、CA,作三角形任意两边的垂直平分线,其交点即为所求。
小试牛刀:
1.已知线段AB和它外一点P,若PA=PB,则点P在
AB的 ;
若点P在AB的 ,则PA=PB.?
高
速
公
路
A
B
在某高速公路l的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么?
生活中的数学
l
能想通为什么吗?
作法:
1、连接AB。
2、作线段AB的垂直平分线
交直线l于点P
则点P为所求的水厂的位置
P
3.如图所示,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在(
)
(A)在AC、BC两边高线的交点处
(B)在AC、BC两边中线的交点处
(C)在AC、BC两边垂直平分线的交点处
(D)在A、B两内角平分线的交点处
解:∵DE垂直平分BC,
∴DB=DC.
∵AC+AD+DC=14
cm,
∴AC+AD+BD=14
cm,
即AC+AB=14
cm.
设AB=x
cm,AC=y
cm.
根据题意,得
解得
答:AB长为8
cm,AC长为6
cm.
4、如图所示,已知AB比AC长2
cm,BC的垂直平分线交AB于D,交BC于点E,
△ACD的周长是14
cm,求AB和AC的长.(学案:课时自测
第4题)
求证:
三角形三边垂直平分线交于一点,且这一点到三角形三个顶点的距离相等。
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理
PB=PC.
∴PA=PC.
∴点P也在边AC的垂直平分线上,且PA=PB=PC
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P也在边AC的垂直平分线上,且PA=PB=PC.
B
A
C
M
N
M’
N’
P
课堂小结
1.本节课学习了哪些知识?
2.通过本节课的学习,你又掌握了哪些
学习方法?
再
见
