【A典学案】冲刺100分 九年级上专题复习第四讲 图形的相似课件(35张PPT)
文档属性
| 名称 | 【A典学案】冲刺100分 九年级上专题复习第四讲 图形的相似课件(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览










文档简介
第四讲 图形的相似
北师大版 九年级上册
知识清单
1.线段的比的定义
在同一单位长度下,两条线段_________的比叫做这两条线段的比.
2.成比例线段
四条线段 a,b,c,d 中,如果 a 与 b 的比等于 c 与 d 的比,即________,那么这四条线段 a,b,c, d 叫做成比例线段.
3.比例的性质
(1)比例的基本性质:如果 a∶b=c∶d,那么________.
(2)合(分)比性质:若 ,则____________.
长度
ad=bc
知识清单
(3)等比性质:若 ,且_______________,则_________________
4.平行线分线段成比例定理及推论
定理:两条直线被一组_________所截,所得的对应线段_________.
推论:平行于三角形一边的直线与其他两边相交,截得的对应线段_________
5.相似多边形的定义
对应角_______,对应边________的两个多边形叫做相似多边形.相似多边形 ___________叫做相似比.
[注意]判定两个多边形相似,对应角相等、对应边成比例,两个条件缺一不可
平行线
成比例
成比例
相等
成比例
对应边的比
知识清单
6.相似多边形的性质
相似多边形的对应角______,对应边______.周长的比等于______,面积的比等于_____________
7.相似三角形的定义
对应角______,对应边________的两个三角形叫做相似三角形.相似三角形
_____________ 叫做相似比.
8.相似三角形的判定方法
(1)_____________;(2)_____________;(3)_______________________.
相等
成比例
相似比
相似比的平方
相等
成比例
对应边的比
两角分别相等
三边成比例
两边成比例且夹角相等
知识清单
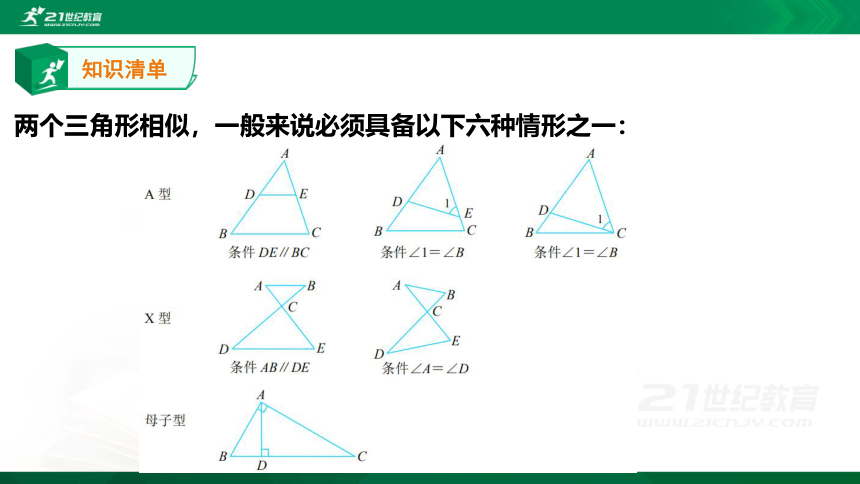
两个三角形相似,一般来说必须具备以下六种情形之一:
知识清单
只要能在复杂图形中辨认出上述基本图形,并能根据问题需要添加适当的辅助线,构造出基本图形,问题即可得以解决.
9.黄金分割
黄金分割的意义:如图,点 C 把线段 AB 分成两条线段 AC 和 BC,如果
__________ ,那么称线段 AB被点 C 黄金分割.其中点 C 叫做线段 AB 的黄金分割点,AC 和 AB 的比叫做__________,黄金分割的比值是一个定值,即 AC∶AB=__________≈0.618.
黄金比
知识清单
10.相似三角形的性质
相似三角形的对应角_______,对应边_______.相似三角形的对应中线的比等于_______,对应高的比等于_______,对应角平分线的比等于_______,周长之比等于_______,相似三角形面积之比等于_________________.
11.测量物体的高度
(1)利用_____________的有关知识测量旗杆(或路灯杆)的高度;
(2)测量的方法有三种:利用__________,利用__________,利用__________
12.位似图形的定义
相等
成比例
相似比
相似比
相似比
相似比
相似比的平方
三角形相似
阳光
标杆
镜子
知识清单
如果两个相似图形的每组对应点所在直线都相交于一点,那么这样的两个图形叫做__________,这个点叫做__________,此时,两个相似图形的相似比又叫做它们的__________.
13.位似图形的性质
位似图形的对应点和位似中心在_______________,它们到位似中心的距离之比等于__________.
位似图形
位似中心
位似比
同一直线上
位似比
典例精讲
类型之一 线段的比与黄金分割
【例 1】如图,在△ABC 中,DE∥BC,交 AB 于点 D,交 AC 于点 E,F 为 BC 上的一点,DE 交 A 于 点 G, ,AE=5,求∶(1) ;(2)AC 的长.
变式训练
1.如图,在△ABC 中,AB=AC=2,BC= -1,∠A=36°,BD 平分∠ABC,交 AC 于点 D,试说明点D 是线段 AC 的黄金分割点.
变式训练
解:在△ABC中,∵AB=AC,∠A=36°,∴∠ABC=∠C=72°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴∠ABD=∠A,∴AD=BD.
∴∠BDC=∠ABD+∠A=72°.
∴∠BDC=∠C.
从而有BC=BD=AD= -1.
,即点D为线段AC的黄金分割点
典例精讲
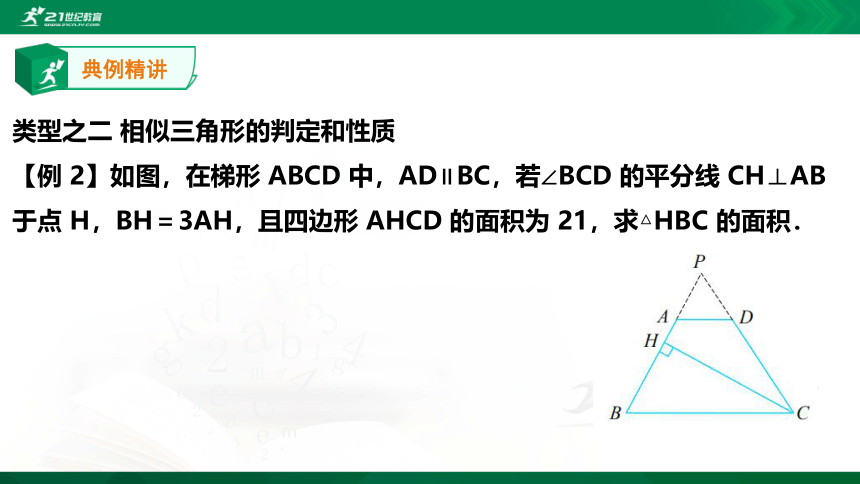
类型之二 相似三角形的判定和性质
【例 2】如图,在梯形 ABCD 中,AD∥BC,若∠BCD 的平分线 CH⊥AB 于点 H,BH=3AH,且四边形 AHCD 的面积为 21,求△HBC 的面积.
典例精讲
[解析]延长 BA,CD 交于点 P,
∵CH⊥AB,CH 平分∠BCD,∴∠B=∠BPC.
∴CB=CP,且 BH=PH. ∵BH=3AH,∴PA∶AB=1∶2,
∴PA∶PB=1∶3. ∵AD∥BC,∴△PAD∽△PBC.
∴S△PAD∶S△PBC=1∶9.
∵S△PCH= S△PBC,∴S△PAD= S△PCH,
∴S△PAD∶S 四边形 AHCD=2∶7. ∵S 四边形 AHCD=21,∴S△PAD=6. ∴S△HBC=S△PCH=27.
变式训练
2.如图,在矩形 ABCD 中,AB=12 cm,BC=6 cm,点 P 沿 AB 边从点 A 开始向点 B 以 2 cm/s 的速度移动,点 Q 沿 DA 从点 D 开始向点 A 以 1 cm/s 的速度移动,如果 P,Q 同时出发,用 t(s)表示运动时
间(0≤t≤6),那么 t 为何值时,以点 Q,A,P 为顶点的三角形与△ABC 相似?
变式训练
解:由题意,得AP=2t,AQ=6-t.
在矩形ABCD中,∠PAQ=∠ABC=90°.
(1)要使△PAQ∽△ABC,则需 ,即 ,解得t=3.
(2)要使△PAQ∽△CBA,则需 ,即 ,解得t=1.2.
∴t为1.2 s或3 s时,以点Q,A,P为顶点的三角形与△ABC相似.
典例精讲
类型之三 构造相似三角形测量物体的高度
【例 3】数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为 1 米的竹竿的影长为0.8 米.同时另一名同学测量这棵树的影子时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图 1),其影高为 1.2 米,落在地面上的影长为 2.4 米,则树高为多少米?
典例精讲
[解析]根据题意,画出如图 2 所示的图形,其中 AB 表示树高,CD 表示落在墙壁上的影子,延长 AC,BD 交于点 E,则 BE 是墙壁不遮挡时树的影长.由太阳光下物体的高度与影长成比例,可知
∴AB=4.2(米).
故树高为 4.2 米.
变式训练
3.一天,某校数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度,来评估这些深坑对河道的影响.如图是同学们选择(确保测量过程中无安全隐患)的测量对象,测量方案如下:
①先测量出沙坑坑沿圆周的周长约为 34.54 米;
②甲同学直立于沙坑坑沿圆周所在平面上,经过适当调整自己所处的位置,当他位于点 B 时,恰好他的视线经过沙坑坑沿圆周上的一点 A 看到坑底 S(甲同学的视线起点 C 与点 A,点 S 三点共线).经测量 AB=1.2 米,BC=1.6 米.
变式训练
根据以上测量数据,求“圆锥形坑”的深度(圆锥的高).(π 取 3.14,结果精确到 0.1 米)
变式训练
解:取圆锥底面圆圆心O,连接OS,OA,
则∠O=∠ABC=90°,OS∥BC,
∴∠ACB=∠ASO.
∴△SOA∽△CBA,
∴“圆锥形坑”的深度约为7.3米.
典例精讲
类型之四 图形的位似
【例 4】如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC 关于 y 轴对称的图形 ,并直接写出点 的坐标;
(2)以原点 O 为位似中心,位似比为 1∶2,在 y 轴的左侧画出△ABC 放大后的图形 ,并直接写出点 的坐标;
(3)如果点 D(a,b)在线段 AB 上,请直接写出经过(2)的变化后点 D 的对应点 的坐标.
典例精讲
[解析](1)如图,点 的坐标为(3,2).
(2)如图,点 的坐标为(-6,4).
(3)如果点 D(a,b)在线段 AB 上,
则经过(2)的变化后点 D 的对应点 的坐标为(2a,2b).
变式训练
4.如图,矩形 ABCD 与矩形 AB′C′D′是位似图形,A 为位似中心,已知矩形 ABCD 的周长为 24,BB′=4,DD′=2.试求 AB 和 AD 的长.
解:∵为矩形ABCD的周长为24,∴AB+AD=12,
设AB=x,则AD=12-x,∴AB′=x+4,AD′=14-x.
又∵矩形ABCD与矩形AB′C′D′时位似图形,
,即 ,解得x=8.
∴AB=8,AD=12-x=12-8=4.
区校真题
1.(光明)如图,已知直线 a∥b∥c,直线 m,n 与 a,b,c 分别交于
点 A,C,E 和 B,D,F,AC=4,CE=6,BD=3,DF=( )
A.7 B.7.5
C.8 D.4.5
2.(龙华)如图,已知 D,E 分别为 AB,AC 上的两点,且 DE∥BC,
AE=2CE,AB=6,则 AD 的长为( )
A.3 B.4
C.5 D.6
D
B
区校真题
3.(南山)如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比为 ,点 A,B,E 在 x 轴上,若正方形 BEFG 的边长为 12,则 C 点坐标为( )
A.(6,4) B.(6,2) C.(4,4) D.(4,2)
A
区校真题
4.(宝安)数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦 CD 的高度,如图所示,点 P 处放一水平的平面镜.光线从点 A 出发经平面镜反射后刚好射到大厦 CD 的顶端 C 处,已知 AB⊥BD,CD⊥BD,且测得 AB=1 米,BP=1.5 米,PD=12 米,那么该大厦的高度约为( )
A.8 米 B.16 米 C.24 米 D.36 米
5.(龙华)如图,在△ABC 中,已知∠C=35°,AD 是 BC 边上的高,且 AD2=BD·CD,则∠B 的度数是__________.
A
55°
区校真题
6.(南山)如图,在矩形 ABCD 中,E 为 AD 边上的一点,过 C 点作 CF⊥CE 交 AB 的延长线于点 F.
(1)求证:△CDE∽△CBF;
(2)若 B 为 AF 的中点,CB=3,DE=1,求 CD 的长.
区校真题
解析:(1)∵四边形ABCD是矩形,∴∠D=∠1=∠2+∠3=90°.
∵CF⊥CE,∴∠4+∠3=90°.∴∠2=∠4.∴△CDE∽△CBF.
(2)∵四边形ABCD是矩形,∴CD=AB.
∵B为AF的中点,∴BF=AB.
∴设CD=BF=x.
∵△CDE∽△CBF,
区校真题
7.(罗湖)如图,某测量工作人员的眼睛 A 与标杆顶端 F、电视塔顶端 E 在同一直线上,已知此人眼睛距地面 1.6 m,标杆为 3.2 m,且 BC=1 m,CD=5 m.试求电视塔的高 ED.
区校真题
解:如图,过点A作AH⊥ED于点H,交FC于点G.
∵AB⊥BD,FC⊥BD,ED⊥BD,∴AB∥FC∥ED,
∴四边形ABDH,ABCG,GCDH是矩形,即∠FGA=∠EHA=90°,
AG=BC=1(m),GH=CD=5(m),DH=GC=AG=1.6(m).
又∵∠FAG=∠EAH,∴△AGF∽△AHE,
∴EH=9.6(m),ED=EH+HD=9.6+1.6=11.2(m).
电视塔的高ED为11.2 m.
中考链接
如图,在△ABC 中,∠A=90°,AB=3,AC=4,点 M,Q 分别是边 AB,BC 上的动点(点 M 不与 A, B 重合),且 MQ⊥BC,过点 M 作 BC 的平行线 MN,交 AC 于点 N,连接 NQ,设 BQ 为 x.
(1)试说明不论 x 为何值时,总有△QBM∽△ABC;
(2)是否存在一点 Q,使得四边形 BMNQ 为平行四边形,试说明理由;
(3)当 x 为何值时,四边形 BMNQ 的面积最大,并求出最大值.
中考链接
解:(1)∵MQ⊥BC,
∴∠MQB=90°,
∴∠MQB=∠CAB,又∠QBM=∠ABC,
∴△QBM∽△ABC;
(2)当BQ=MN时,四边形BMNQ为平行四边形,
∵MN∥BQ,BQ=MN,
∴四边形BMNQ为平行四边形;
(3)∵∠A=90°,AB=3,AC=4,
中考链接
∵△QBM∽△ABC,
∴当x= 时,四边形BMNQ的面积最大,最大值为
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版 九年级上册
知识清单
1.线段的比的定义
在同一单位长度下,两条线段_________的比叫做这两条线段的比.
2.成比例线段
四条线段 a,b,c,d 中,如果 a 与 b 的比等于 c 与 d 的比,即________,那么这四条线段 a,b,c, d 叫做成比例线段.
3.比例的性质
(1)比例的基本性质:如果 a∶b=c∶d,那么________.
(2)合(分)比性质:若 ,则____________.
长度
ad=bc
知识清单
(3)等比性质:若 ,且_______________,则_________________
4.平行线分线段成比例定理及推论
定理:两条直线被一组_________所截,所得的对应线段_________.
推论:平行于三角形一边的直线与其他两边相交,截得的对应线段_________
5.相似多边形的定义
对应角_______,对应边________的两个多边形叫做相似多边形.相似多边形 ___________叫做相似比.
[注意]判定两个多边形相似,对应角相等、对应边成比例,两个条件缺一不可
平行线
成比例
成比例
相等
成比例
对应边的比
知识清单
6.相似多边形的性质
相似多边形的对应角______,对应边______.周长的比等于______,面积的比等于_____________
7.相似三角形的定义
对应角______,对应边________的两个三角形叫做相似三角形.相似三角形
_____________ 叫做相似比.
8.相似三角形的判定方法
(1)_____________;(2)_____________;(3)_______________________.
相等
成比例
相似比
相似比的平方
相等
成比例
对应边的比
两角分别相等
三边成比例
两边成比例且夹角相等
知识清单
两个三角形相似,一般来说必须具备以下六种情形之一:
知识清单
只要能在复杂图形中辨认出上述基本图形,并能根据问题需要添加适当的辅助线,构造出基本图形,问题即可得以解决.
9.黄金分割
黄金分割的意义:如图,点 C 把线段 AB 分成两条线段 AC 和 BC,如果
__________ ,那么称线段 AB被点 C 黄金分割.其中点 C 叫做线段 AB 的黄金分割点,AC 和 AB 的比叫做__________,黄金分割的比值是一个定值,即 AC∶AB=__________≈0.618.
黄金比
知识清单
10.相似三角形的性质
相似三角形的对应角_______,对应边_______.相似三角形的对应中线的比等于_______,对应高的比等于_______,对应角平分线的比等于_______,周长之比等于_______,相似三角形面积之比等于_________________.
11.测量物体的高度
(1)利用_____________的有关知识测量旗杆(或路灯杆)的高度;
(2)测量的方法有三种:利用__________,利用__________,利用__________
12.位似图形的定义
相等
成比例
相似比
相似比
相似比
相似比
相似比的平方
三角形相似
阳光
标杆
镜子
知识清单
如果两个相似图形的每组对应点所在直线都相交于一点,那么这样的两个图形叫做__________,这个点叫做__________,此时,两个相似图形的相似比又叫做它们的__________.
13.位似图形的性质
位似图形的对应点和位似中心在_______________,它们到位似中心的距离之比等于__________.
位似图形
位似中心
位似比
同一直线上
位似比
典例精讲
类型之一 线段的比与黄金分割
【例 1】如图,在△ABC 中,DE∥BC,交 AB 于点 D,交 AC 于点 E,F 为 BC 上的一点,DE 交 A 于 点 G, ,AE=5,求∶(1) ;(2)AC 的长.
变式训练
1.如图,在△ABC 中,AB=AC=2,BC= -1,∠A=36°,BD 平分∠ABC,交 AC 于点 D,试说明点D 是线段 AC 的黄金分割点.
变式训练
解:在△ABC中,∵AB=AC,∠A=36°,∴∠ABC=∠C=72°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴∠ABD=∠A,∴AD=BD.
∴∠BDC=∠ABD+∠A=72°.
∴∠BDC=∠C.
从而有BC=BD=AD= -1.
,即点D为线段AC的黄金分割点
典例精讲
类型之二 相似三角形的判定和性质
【例 2】如图,在梯形 ABCD 中,AD∥BC,若∠BCD 的平分线 CH⊥AB 于点 H,BH=3AH,且四边形 AHCD 的面积为 21,求△HBC 的面积.
典例精讲
[解析]延长 BA,CD 交于点 P,
∵CH⊥AB,CH 平分∠BCD,∴∠B=∠BPC.
∴CB=CP,且 BH=PH. ∵BH=3AH,∴PA∶AB=1∶2,
∴PA∶PB=1∶3. ∵AD∥BC,∴△PAD∽△PBC.
∴S△PAD∶S△PBC=1∶9.
∵S△PCH= S△PBC,∴S△PAD= S△PCH,
∴S△PAD∶S 四边形 AHCD=2∶7. ∵S 四边形 AHCD=21,∴S△PAD=6. ∴S△HBC=S△PCH=27.
变式训练
2.如图,在矩形 ABCD 中,AB=12 cm,BC=6 cm,点 P 沿 AB 边从点 A 开始向点 B 以 2 cm/s 的速度移动,点 Q 沿 DA 从点 D 开始向点 A 以 1 cm/s 的速度移动,如果 P,Q 同时出发,用 t(s)表示运动时
间(0≤t≤6),那么 t 为何值时,以点 Q,A,P 为顶点的三角形与△ABC 相似?
变式训练
解:由题意,得AP=2t,AQ=6-t.
在矩形ABCD中,∠PAQ=∠ABC=90°.
(1)要使△PAQ∽△ABC,则需 ,即 ,解得t=3.
(2)要使△PAQ∽△CBA,则需 ,即 ,解得t=1.2.
∴t为1.2 s或3 s时,以点Q,A,P为顶点的三角形与△ABC相似.
典例精讲
类型之三 构造相似三角形测量物体的高度
【例 3】数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为 1 米的竹竿的影长为0.8 米.同时另一名同学测量这棵树的影子时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图 1),其影高为 1.2 米,落在地面上的影长为 2.4 米,则树高为多少米?
典例精讲
[解析]根据题意,画出如图 2 所示的图形,其中 AB 表示树高,CD 表示落在墙壁上的影子,延长 AC,BD 交于点 E,则 BE 是墙壁不遮挡时树的影长.由太阳光下物体的高度与影长成比例,可知
∴AB=4.2(米).
故树高为 4.2 米.
变式训练
3.一天,某校数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度,来评估这些深坑对河道的影响.如图是同学们选择(确保测量过程中无安全隐患)的测量对象,测量方案如下:
①先测量出沙坑坑沿圆周的周长约为 34.54 米;
②甲同学直立于沙坑坑沿圆周所在平面上,经过适当调整自己所处的位置,当他位于点 B 时,恰好他的视线经过沙坑坑沿圆周上的一点 A 看到坑底 S(甲同学的视线起点 C 与点 A,点 S 三点共线).经测量 AB=1.2 米,BC=1.6 米.
变式训练
根据以上测量数据,求“圆锥形坑”的深度(圆锥的高).(π 取 3.14,结果精确到 0.1 米)
变式训练
解:取圆锥底面圆圆心O,连接OS,OA,
则∠O=∠ABC=90°,OS∥BC,
∴∠ACB=∠ASO.
∴△SOA∽△CBA,
∴“圆锥形坑”的深度约为7.3米.
典例精讲
类型之四 图形的位似
【例 4】如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC 关于 y 轴对称的图形 ,并直接写出点 的坐标;
(2)以原点 O 为位似中心,位似比为 1∶2,在 y 轴的左侧画出△ABC 放大后的图形 ,并直接写出点 的坐标;
(3)如果点 D(a,b)在线段 AB 上,请直接写出经过(2)的变化后点 D 的对应点 的坐标.
典例精讲
[解析](1)如图,点 的坐标为(3,2).
(2)如图,点 的坐标为(-6,4).
(3)如果点 D(a,b)在线段 AB 上,
则经过(2)的变化后点 D 的对应点 的坐标为(2a,2b).
变式训练
4.如图,矩形 ABCD 与矩形 AB′C′D′是位似图形,A 为位似中心,已知矩形 ABCD 的周长为 24,BB′=4,DD′=2.试求 AB 和 AD 的长.
解:∵为矩形ABCD的周长为24,∴AB+AD=12,
设AB=x,则AD=12-x,∴AB′=x+4,AD′=14-x.
又∵矩形ABCD与矩形AB′C′D′时位似图形,
,即 ,解得x=8.
∴AB=8,AD=12-x=12-8=4.
区校真题
1.(光明)如图,已知直线 a∥b∥c,直线 m,n 与 a,b,c 分别交于
点 A,C,E 和 B,D,F,AC=4,CE=6,BD=3,DF=( )
A.7 B.7.5
C.8 D.4.5
2.(龙华)如图,已知 D,E 分别为 AB,AC 上的两点,且 DE∥BC,
AE=2CE,AB=6,则 AD 的长为( )
A.3 B.4
C.5 D.6
D
B
区校真题
3.(南山)如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比为 ,点 A,B,E 在 x 轴上,若正方形 BEFG 的边长为 12,则 C 点坐标为( )
A.(6,4) B.(6,2) C.(4,4) D.(4,2)
A
区校真题
4.(宝安)数学兴趣小组的同学们来到宝安区海淀广场,设计用手电来测量广场附近某大厦 CD 的高度,如图所示,点 P 处放一水平的平面镜.光线从点 A 出发经平面镜反射后刚好射到大厦 CD 的顶端 C 处,已知 AB⊥BD,CD⊥BD,且测得 AB=1 米,BP=1.5 米,PD=12 米,那么该大厦的高度约为( )
A.8 米 B.16 米 C.24 米 D.36 米
5.(龙华)如图,在△ABC 中,已知∠C=35°,AD 是 BC 边上的高,且 AD2=BD·CD,则∠B 的度数是__________.
A
55°
区校真题
6.(南山)如图,在矩形 ABCD 中,E 为 AD 边上的一点,过 C 点作 CF⊥CE 交 AB 的延长线于点 F.
(1)求证:△CDE∽△CBF;
(2)若 B 为 AF 的中点,CB=3,DE=1,求 CD 的长.
区校真题
解析:(1)∵四边形ABCD是矩形,∴∠D=∠1=∠2+∠3=90°.
∵CF⊥CE,∴∠4+∠3=90°.∴∠2=∠4.∴△CDE∽△CBF.
(2)∵四边形ABCD是矩形,∴CD=AB.
∵B为AF的中点,∴BF=AB.
∴设CD=BF=x.
∵△CDE∽△CBF,
区校真题
7.(罗湖)如图,某测量工作人员的眼睛 A 与标杆顶端 F、电视塔顶端 E 在同一直线上,已知此人眼睛距地面 1.6 m,标杆为 3.2 m,且 BC=1 m,CD=5 m.试求电视塔的高 ED.
区校真题
解:如图,过点A作AH⊥ED于点H,交FC于点G.
∵AB⊥BD,FC⊥BD,ED⊥BD,∴AB∥FC∥ED,
∴四边形ABDH,ABCG,GCDH是矩形,即∠FGA=∠EHA=90°,
AG=BC=1(m),GH=CD=5(m),DH=GC=AG=1.6(m).
又∵∠FAG=∠EAH,∴△AGF∽△AHE,
∴EH=9.6(m),ED=EH+HD=9.6+1.6=11.2(m).
电视塔的高ED为11.2 m.
中考链接
如图,在△ABC 中,∠A=90°,AB=3,AC=4,点 M,Q 分别是边 AB,BC 上的动点(点 M 不与 A, B 重合),且 MQ⊥BC,过点 M 作 BC 的平行线 MN,交 AC 于点 N,连接 NQ,设 BQ 为 x.
(1)试说明不论 x 为何值时,总有△QBM∽△ABC;
(2)是否存在一点 Q,使得四边形 BMNQ 为平行四边形,试说明理由;
(3)当 x 为何值时,四边形 BMNQ 的面积最大,并求出最大值.
中考链接
解:(1)∵MQ⊥BC,
∴∠MQB=90°,
∴∠MQB=∠CAB,又∠QBM=∠ABC,
∴△QBM∽△ABC;
(2)当BQ=MN时,四边形BMNQ为平行四边形,
∵MN∥BQ,BQ=MN,
∴四边形BMNQ为平行四边形;
(3)∵∠A=90°,AB=3,AC=4,
中考链接
∵△QBM∽△ABC,
∴当x= 时,四边形BMNQ的面积最大,最大值为
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
