5.6_应用一元一次方程-追赶小明 课件(共30张PPT)
文档属性
| 名称 | 5.6_应用一元一次方程-追赶小明 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 11:32:19 | ||
图片预览











文档简介
模拟试验
小明和小华相距10米,他们同时出发,相向而行,小明每秒走3米,小华每秒走4米,他们能相遇吗?几秒钟可以相遇?
等量关系:
小明走的路程+小华走的路程=相距的路程
所用公式:路程=速度×时间
导入新课
情境引入
你知道它蕴含的是我们数学中的什么问题吗?
6 应用一元一次方程
——追赶小明
学习目标
1.学会利用线段图分析行程问题,寻找等量关系,
建立数学模型.(难点)
2.能利用行程中的速度、路程、时间之间的关系列
方程解应用题.(重点)
导入新知
想一想
速度、路程、时间之间的关系
1.行程问题中速度、时间和路程的关系是:路程=________×________.
2.行程问题分为两类:一类是____________;另一类是____________.借助“线段图”分析题意,找出等量关系,正确地列出方程并求解.
速度
时间
相遇问题
追及问题
做一做
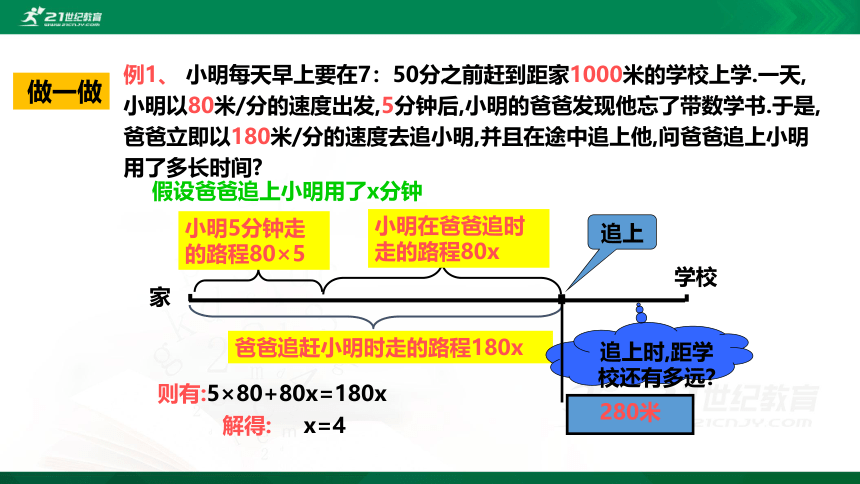
则有:5×80+80x=180x
家
学校
追上
小明5分钟走的路程80×5
小明在爸爸追时走的路程80x
爸爸追赶小明时走的路程180x
追上时,距学校还有多远?
解得: x=4
280米
假设爸爸追上小明用了x分钟
例1、 小明每天早上要在7:50分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间?
解(1)设爸爸追上小明用了x分钟,
据题意,得
180x=80x+80×5
解得x=4
因此,爸爸追上小明用了4分。
(2)因为 180×4=720(米)
1000-720=280(米)
所以,追上小明时,距离学校还有280米。
做一做
例2 已知船在静水中的速度是24千米/时,水流速度是2千米/时,该船在甲、乙两地间行驶一个来回共用了24小时,
求甲、乙两地的距离是多少?
分析:本题是行程问题,故有:
路程=平均速度×时间;
时间=路程÷平均速度.
但涉及水流速度,必须要掌握:
顺水速度=船速+水速;
逆水速度=船速-水速.
想一想
想一想,这道题
是不是只有这一
种解法呢?
直接设元法
解 设汽船顺水航行从甲地到乙地需x 小时,
则汽船逆水航行的距离是(24-2)(24-x)千米,
顺水航行的距离是(24 +2)x千米.
等量关系:汽船顺水航行的距离=汽船逆水航行的距离.
(24 +2) ×11=286
答:甲、乙两地距离为286千米.
依题意,得:
(24-2)(24-x)= (24+2)x
x=11
解方程,得:
间接设元法
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
育红学校七年级学生步行到郊外旅行:(1)班的学生组成前队,步行速度为4千米/时,(2)班的学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
根据上面的事实提出问题并尝试去解答.
议一议
问题1:后队追上前队用了多长时间 ?
解:设后队追上前队用了x小时,由题意得:
6x = 4x + 4
解方程得:x =2
答:后队追上前队时用了2小时。
问题2:后队追上前队时联络员行了多少路程?
解:由问题1得后队追上前队用了2小时,因此,联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,
由题意得:
12x = 4x + 4
解方程得:x =0.5
答:联络员第一次追上前队时用了0.5小时。
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
甲、乙两人同向出发,甲追乙这类问题为追及问题:
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
甲出发地
乙出发地
追及地
乙的行程
甲的行程
归纳
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
乙先走的路程
乙后走的路程
甲的行程
甲、乙出发地
追及地
典例精析
[解析] 设妹妹用时x分钟,由路程相等列出方程90×75×16=100×60x,解得x=18.
例3 哥哥上学平均每分钟走90步,每步长75cm,用16分钟到学校;妹妹沿同一条路上学,每分钟走100步,每步长60cm,则妹妹到校所用的时间是_____分钟.
18
例4汽船从甲地顺水开往乙地,所用时间比从乙地逆水开往甲地少1.5小时.已知船在静水的速度为18千米/时,水流速度为2千米/小时,求甲、乙两地之间的距离?
分析:本题是行程问题,故有:
路程=平均速度×时间;
时间=路程÷平均速度.
但涉及水流速度,必须要掌握:
顺水速度=船速+水速;
逆水速度=船速-水速.
解:设甲、乙两地的距离为x 千米,
等量关系:逆水所用时间-顺水所用时间=1.5
依题意,得
解方程,得 x =120
答:甲乙两地之间的距离为120千米.
想一想,这道题
是不是只有这一
种解法呢?
方法一
直接设元法
方法二
解 设汽船逆水航行从乙地到甲地需x 小时,
则汽船顺水航行的距离是(18+2)(x-1.5)千米,
逆水航行的距离是(18 -2)x千米.
等量关系:汽船顺水航行的距离=汽船逆水航行的距离.
(18 -2) ×7.5=120
答:甲、乙两地距离为120千米.
依题意,得:
(18+2)(x -1.5)= (18 -2)x
x=7.5
解方程,得:
间接设元法
例3 小明早晨要在7:20以前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现 他忘了带历史作业,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学
校还有多远?
追及问题
分析:当爸爸追上小明时,两人所走路程相等.
解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x=180x.
答:爸爸追上小明用了4分钟.
(2)180×4=720(米),1000-720=280(米).
答:追上小明时,距离学校还有280米.
解得 x=4.
80×5
80x
180x
议一议
问题2:操场一周是400米,小明每秒跑5米,小强骑自行车每秒15米,两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
解:设经过x秒两人第一次相遇,依题意,得
15x-5x=400,
解得x=40.
答:经过40秒两人第一次相遇
操场一周是400米,小明每秒跑5米,小华骑自行车每秒15米,两人绕跑道同时同地同向而行,两人同时同地相背而行,则两个人何时相遇?
解:设经过x秒两人第一次相遇,依题意,得
15x+5x=400,
解得x=20 .
答:经过 20 秒两人第一次相遇
归纳
环形跑道长s米,设v甲>v乙,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:
v甲t-v乙t=s.
②同时同地、背向而行:
v甲t+v乙t=s.
环形跑道问题
追及问题
相遇问题
1.小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为x千米/时,
列方程得( )
A.4+3x=25.2 B.3×4+x=25.2
C.3(4+x)=25.2 D.3(x-4)=25.2
C
2.一列长30米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,这位同学走的路程为____米,速度是____米/分.
90
90
3.一架飞机在两城市之间飞行,风速为24千米/时,顺风飞行需要2小时50分,逆风飞行需要3小时.
求无风时飞机的飞行速度和两城之间的航程.
4.敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗,问战斗是在开始追击后几小时发生的?
解:设战斗是在开始追击后x小时发生的.
根据题意,得 8x-5x=25-1.
解得 x=8.
答:战斗是在开始追击后8小时发生的.
问题的已
知条件
解决行程问题的基本步骤:
画出线
段图
找出等
量关系
列方程
并求解
回答
同向追及问题
同地不同时:
同时不同地:
甲路程+路程差=乙路程;
甲路程=乙路程
相向相遇问题
甲的路程+乙的路程=总路程
课堂小结
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
小明和小华相距10米,他们同时出发,相向而行,小明每秒走3米,小华每秒走4米,他们能相遇吗?几秒钟可以相遇?
等量关系:
小明走的路程+小华走的路程=相距的路程
所用公式:路程=速度×时间
导入新课
情境引入
你知道它蕴含的是我们数学中的什么问题吗?
6 应用一元一次方程
——追赶小明
学习目标
1.学会利用线段图分析行程问题,寻找等量关系,
建立数学模型.(难点)
2.能利用行程中的速度、路程、时间之间的关系列
方程解应用题.(重点)
导入新知
想一想
速度、路程、时间之间的关系
1.行程问题中速度、时间和路程的关系是:路程=________×________.
2.行程问题分为两类:一类是____________;另一类是____________.借助“线段图”分析题意,找出等量关系,正确地列出方程并求解.
速度
时间
相遇问题
追及问题
做一做
则有:5×80+80x=180x
家
学校
追上
小明5分钟走的路程80×5
小明在爸爸追时走的路程80x
爸爸追赶小明时走的路程180x
追上时,距学校还有多远?
解得: x=4
280米
假设爸爸追上小明用了x分钟
例1、 小明每天早上要在7:50分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带数学书.于是,爸爸立即以180米/分的速度去追小明,并且在途中追上他,问爸爸追上小明用了多长时间?
解(1)设爸爸追上小明用了x分钟,
据题意,得
180x=80x+80×5
解得x=4
因此,爸爸追上小明用了4分。
(2)因为 180×4=720(米)
1000-720=280(米)
所以,追上小明时,距离学校还有280米。
做一做
例2 已知船在静水中的速度是24千米/时,水流速度是2千米/时,该船在甲、乙两地间行驶一个来回共用了24小时,
求甲、乙两地的距离是多少?
分析:本题是行程问题,故有:
路程=平均速度×时间;
时间=路程÷平均速度.
但涉及水流速度,必须要掌握:
顺水速度=船速+水速;
逆水速度=船速-水速.
想一想
想一想,这道题
是不是只有这一
种解法呢?
直接设元法
解 设汽船顺水航行从甲地到乙地需x 小时,
则汽船逆水航行的距离是(24-2)(24-x)千米,
顺水航行的距离是(24 +2)x千米.
等量关系:汽船顺水航行的距离=汽船逆水航行的距离.
(24 +2) ×11=286
答:甲、乙两地距离为286千米.
依题意,得:
(24-2)(24-x)= (24+2)x
x=11
解方程,得:
间接设元法
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
育红学校七年级学生步行到郊外旅行:(1)班的学生组成前队,步行速度为4千米/时,(2)班的学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
根据上面的事实提出问题并尝试去解答.
议一议
问题1:后队追上前队用了多长时间 ?
解:设后队追上前队用了x小时,由题意得:
6x = 4x + 4
解方程得:x =2
答:后队追上前队时用了2小时。
问题2:后队追上前队时联络员行了多少路程?
解:由问题1得后队追上前队用了2小时,因此,联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,
由题意得:
12x = 4x + 4
解方程得:x =0.5
答:联络员第一次追上前队时用了0.5小时。
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
甲、乙两人同向出发,甲追乙这类问题为追及问题:
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
甲出发地
乙出发地
追及地
乙的行程
甲的行程
归纳
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
注意:同向而行注意始发时间和地点.
乙先走的路程
乙后走的路程
甲的行程
甲、乙出发地
追及地
典例精析
[解析] 设妹妹用时x分钟,由路程相等列出方程90×75×16=100×60x,解得x=18.
例3 哥哥上学平均每分钟走90步,每步长75cm,用16分钟到学校;妹妹沿同一条路上学,每分钟走100步,每步长60cm,则妹妹到校所用的时间是_____分钟.
18
例4汽船从甲地顺水开往乙地,所用时间比从乙地逆水开往甲地少1.5小时.已知船在静水的速度为18千米/时,水流速度为2千米/小时,求甲、乙两地之间的距离?
分析:本题是行程问题,故有:
路程=平均速度×时间;
时间=路程÷平均速度.
但涉及水流速度,必须要掌握:
顺水速度=船速+水速;
逆水速度=船速-水速.
解:设甲、乙两地的距离为x 千米,
等量关系:逆水所用时间-顺水所用时间=1.5
依题意,得
解方程,得 x =120
答:甲乙两地之间的距离为120千米.
想一想,这道题
是不是只有这一
种解法呢?
方法一
直接设元法
方法二
解 设汽船逆水航行从乙地到甲地需x 小时,
则汽船顺水航行的距离是(18+2)(x-1.5)千米,
逆水航行的距离是(18 -2)x千米.
等量关系:汽船顺水航行的距离=汽船逆水航行的距离.
(18 -2) ×7.5=120
答:甲、乙两地距离为120千米.
依题意,得:
(18+2)(x -1.5)= (18 -2)x
x=7.5
解方程,得:
间接设元法
例3 小明早晨要在7:20以前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现 他忘了带历史作业,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学
校还有多远?
追及问题
分析:当爸爸追上小明时,两人所走路程相等.
解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x=180x.
答:爸爸追上小明用了4分钟.
(2)180×4=720(米),1000-720=280(米).
答:追上小明时,距离学校还有280米.
解得 x=4.
80×5
80x
180x
议一议
问题2:操场一周是400米,小明每秒跑5米,小强骑自行车每秒15米,两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
解:设经过x秒两人第一次相遇,依题意,得
15x-5x=400,
解得x=40.
答:经过40秒两人第一次相遇
操场一周是400米,小明每秒跑5米,小华骑自行车每秒15米,两人绕跑道同时同地同向而行,两人同时同地相背而行,则两个人何时相遇?
解:设经过x秒两人第一次相遇,依题意,得
15x+5x=400,
解得x=20 .
答:经过 20 秒两人第一次相遇
归纳
环形跑道长s米,设v甲>v乙,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:
v甲t-v乙t=s.
②同时同地、背向而行:
v甲t+v乙t=s.
环形跑道问题
追及问题
相遇问题
1.小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为x千米/时,
列方程得( )
A.4+3x=25.2 B.3×4+x=25.2
C.3(4+x)=25.2 D.3(x-4)=25.2
C
2.一列长30米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,这位同学走的路程为____米,速度是____米/分.
90
90
3.一架飞机在两城市之间飞行,风速为24千米/时,顺风飞行需要2小时50分,逆风飞行需要3小时.
求无风时飞机的飞行速度和两城之间的航程.
4.敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗,问战斗是在开始追击后几小时发生的?
解:设战斗是在开始追击后x小时发生的.
根据题意,得 8x-5x=25-1.
解得 x=8.
答:战斗是在开始追击后8小时发生的.
问题的已
知条件
解决行程问题的基本步骤:
画出线
段图
找出等
量关系
列方程
并求解
回答
同向追及问题
同地不同时:
同时不同地:
甲路程+路程差=乙路程;
甲路程=乙路程
相向相遇问题
甲的路程+乙的路程=总路程
课堂小结
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
