人教版小学数学六年级上册第八单元数学广角--数与形单元检测(二)卷(含答案)
文档属性
| 名称 | 人教版小学数学六年级上册第八单元数学广角--数与形单元检测(二)卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 10:24:43 | ||
图片预览

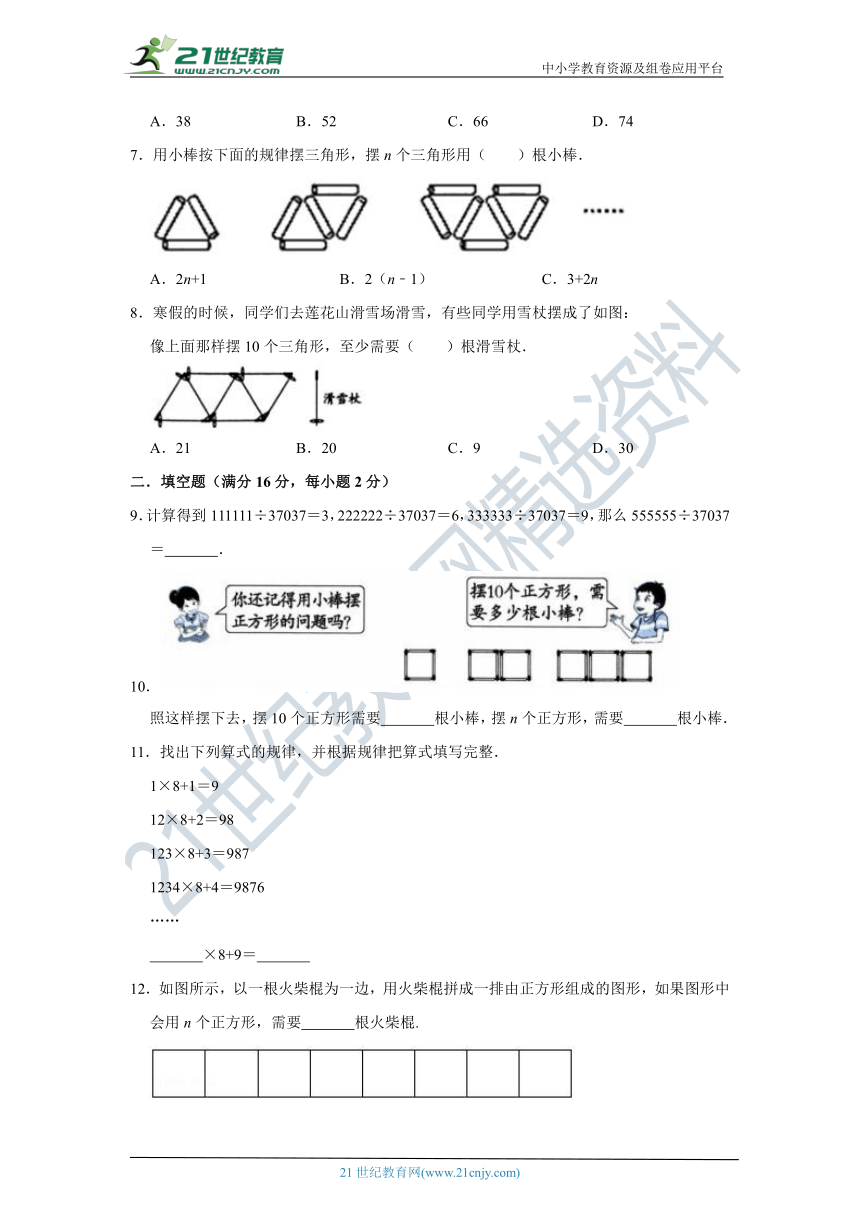


文档简介
中小学教育资源及组卷应用平台
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(二)卷
一.选择题(满分16分,每小题2分)
1.如图,按这样的规律第7个图形有( )个点.
A.21 B.25 C.28 D.29
2.根据1÷11=0.,2÷11=0.,3÷11=0.,可以推出9÷11=( )
A.0. B.0. C.0. D.0.
3.将一些小圆球如图摆放,第6幅图有( )个小圆球.
A.30 B.42 C.56
4.2×9=18,22×_99???217_8,222×999=221778,2222×9999=22217778,22222×99999=( )21cnjy.com
A.22117788 B.2222177778 C.222221778 D.2222177788
5.如图所示,在图_???1????????????_重叠的三角形共有4个,在图(2)中互不重叠的三角形共有7个,在图(3)中互不重叠的三角形共有10个,……,则在图(6)中,互不重叠的三角形共有( )21·cn·jy·com
A.10个 B.15个 C.19个 D.22个
6.填在如图各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A.38 B.52 C.66 D.74
7.用小棒按下面的规律摆三角形,摆n个三角形用( )根小棒.
A.2n+1 B.2(n﹣1) C.3+2n
8.寒假的时候,同学们去莲花山滑雪场滑雪,有些同学用雪杖摆成了如图:
像上面那样摆10个三角形,至少需要( )根滑雪杖.
A.21 B.20 C.9 D.30
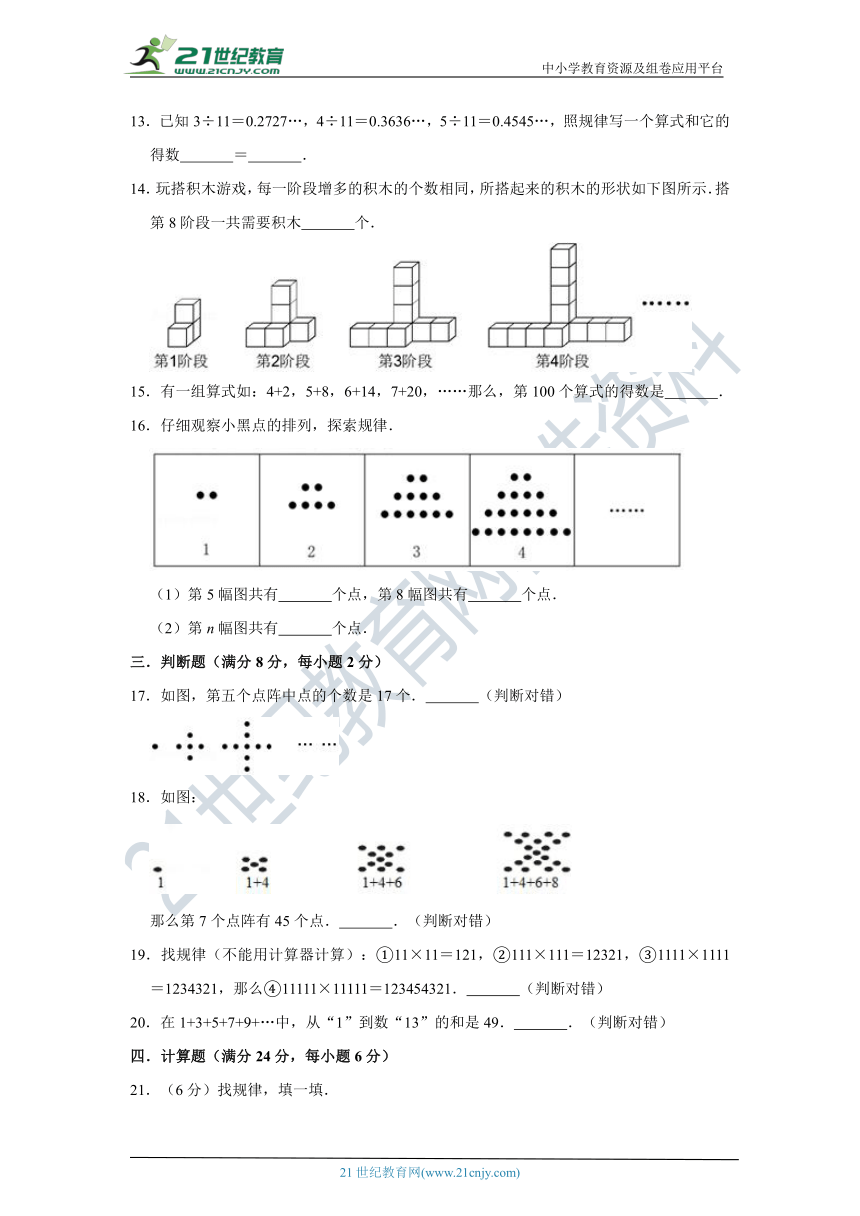
二.填空题(满分16分,每小题2分)
9.计算得到11_1111?·3_7037=3,222222÷37037=6,333333÷37037=9,那么555555÷37037= .www.21-cn-jy.com
10.
照这样摆下去,摆10个正方形需要 根小棒,摆n个正方形,需要 根小棒.
11.找出下列算式的规律,并根据规律把算式填写完整.
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
×8+9=
12.如图所示,以一根火柴棍为一边,用火柴棍拼成一排由正方形组成的图形,如果图形中会用n个正方形,需要 根火柴棍.2·1·c·n·j·y
13.已知3÷11=0.2727…,4÷11=0.3636…,5÷11=0.4545…,照规律写一个算式和它的得数 = .【来源:21·世纪·教育·网】
14.玩搭积木游戏,每一阶段增多的积木的个数相同,所搭起来的积木的形状如下图所示.搭第8阶段一共需要积木 个.21·世纪*教育网
15.有一组算式如:4+2,5+8,6+14,7+20,……那么,第100个算式的得数是 .
16.仔细观察小黑点的排列,探索规律.
(1)第5幅图共有 个点,第8幅图共有 个点.
(2)第n幅图共有 个点.
三.判断题(满分8分,每小题2分)
17.如图,第五个点阵中点的个数是17个. (判断对错)
18.如图:
那么第7个点阵有45个点. .(判断对错)
19.找规律(不能用计算器计算_?????????11??_11=121,②111×111=12321,③1111×1111=1234321,那么④11111×11111=123454321. (判断对错)
20.在1+3+5+7+9+…中,从“1”到数“13”的和是49. .(判断对错)
四.计算题(满分24分,每小题6分)
21.(6分)找规律,填一填.
22.(6分)按规律填出下面算式的得数.
(1)98×9=
987×9=
9876×9=
9875×9=
(2)12×8+2=
123×8+3=
1234×8+4=
12345×8+5=
23.(6分)填一填.
24.(6分)按图摆放餐桌和椅子,摆8张餐桌可以坐多少人?52人用餐,需要摆多少张餐桌?
五.应用题(满分24分,每小题12分)
25.(12分)用小棒按下面的方式拼图形.
(1)如果按下面的规律拼成5个这样的五边形,一共要用 根小棒.
五边形
个数 拼成的形状 小棒根数
1
5
2
9
3
13
4
17
(2)接着拼下去,一共用了57根小棒,你知道一共拼成了多少个五边形吗?
26.(12分)表中一共有50个奇数,实线框出的5个数之和是115,仔细观察后回答问题.
(1)你能发现每次框出的5个数的和与中间数有什么关系?
(2)如果框出的5个数的和是255,应该怎样框?(用彩笔在图中框一框)
(3)能框出和是200的5个数吗?为什么?
(4)一共可以框出多少个大小不同的和?
六.操作题(满分12分,每小题6分)
27.(6分)找规律,画出表示“23”的图形.
28.(6分)(1)你根据下面图形与数的规律接着画一画,填一填.
(2)如果不画,这样排列下去,第10个数是多少?
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(二)卷
参考答案与试题解析
一.选择题(满分16分,每小题2分)
1.答案:B
第1个图形点数是1,
第2个图形点数是5,
第3个图形点数是9,则:
第4个图形点数是:9+4=13,
第5个图形点数是:13+4=17,
第6个图形点数是:17+4=21,
第7个图形点数是:21+4=25.
2.答案:D
根据题意与分析可得:
根据1÷11=0.,2÷11=0.,3÷11=0.,可以推出9÷11=0..
3.答案:B
观察图形可知:
第一个图形中有1×2=2个小圆球,
第二个图形中有2×3=6个小圆球,
第三个图形中有3×4=12个小圆球,
第四个图形中有4×5=20个小圆球,
…
所以第六幅图有6×7=42个小圆球.
4.答案:B
2×9=18
22×99=2178
222×999=221778
2222×9999=22217778
22222×99999=2222177778.
5.答案:C
在图(1)中互不重叠的三角形共有4个
在图(2)中互不重叠的三角形共有7个
在图(3)中互不重叠的三角形共有10个
……
在图n中互不重叠的三角形共4+3(n﹣1)=(3n+1)个
在图(6)中,互不重叠的三角形共有:
3×6+1
=18+1
=19(个)
答:在图(6)中,互不重叠的三角形共有19个。
6.答案:D
根据图形的规律,第4个图形:
左上数字为:2×4﹣2=6
左下应该是4×2=8
右上数字为:4×2+2=10
右下数字为:8×10﹣6=74
答:m的值是74.
7.答案:A
根据题干分析可得,当有n个三角形时小棒的数量就是:
3+2(n﹣1)
=3+2n﹣2
=2n+1(根)
答:摆n个三角形需要 2n+1根小棒.
8.答案:A
摆1个三角形,需要滑雪杖:3根
摆2个三角形,需要滑雪杖:3+2=5(根)
摆3个三角形,需要滑雪杖:3+2+2=7(根)
……
摆n个三角形,需要滑雪杖:3+2(n﹣1)=(2n+1)根
……
摆10个三角形需要滑雪杖:
2×10+1
=20+1
=21(根)
答:摆10个三角形,至少需要21根滑滑雪杖.
二.填空题(满分16分,每小题2分)
9.答案:15.
111111÷37037=3
222222÷37037=6
333333÷37037=9
……
商等于3乘被除数的每个数个位上的数的积
3×5=15
所以:555555÷37037=15
10.答案:40;4n。
根据题干分析可得:
摆一个正方形需要4根小棒,
摆两个正方形需要4×2=8根小棒,
摆三个正方形需要4×3=12根小棒,
…,
摆10个正方形需要10×4=40(根)
据此可得摆n个正方形需要4n根小棒,
答:摆10个正方形需要40根小棒,摆n个正方形,需要4n根小棒.
11.答案:见试题解答内容
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
123456789×8+9=987654321
12.答案:(3n+1)。
摆1个正方形需要火柴棍4根
摆2个正方形需要火柴棍4+3=7(根)
摆3个正方形需要火柴棍4+3+3=10(根)
……
摆n个正方形需要火柴棍4+3(n﹣1)=(3n+1)根
答:n个正方形,需要(3n+1)根火柴棍.
13.答案:9÷11;0.8181…(答案不唯一).
根据商的变化规律可知,
1÷11=0.0909…
2÷11=0.1818…
3÷11=0.2727…
4÷11=0.3636…
5÷11=0.4545…
6÷11=0.5454…
7÷11=0.6363…
8÷11=0.7272…
9÷11=0.8181…
14.答案:24.
根据题干分析可得:第n阶段,积木个数是3n;
当n=8时,3×8=24(个),
答:第8阶段有24个积木.
15.答案:699.
这组算式的规律是得数每次加7,
第1个算式得数是6,
第2个算式的得数是6+7=13,
第3个算式的得数是6+7×2=20,
第4个算式的得数是6+7×3=27,
……;
第100个算式的得数就是:
6+7×(100﹣1)=699
答:第100个算式的得数是 699.
16.答案:30;72;n(n+1).
第一幅图小黑点的个数为2个
第二幅图小黑点的个数:2+4=6(个)
第三幅图小黑点的个数为:2+4+6=12(个)
……
第n副图小黑点的个数为:2×(1+2+……+n)=n(n+1)个
(1)5×(5+1)
=5×6
=30(个)
8×(8+1)
=8×9
=72(个)
答:第5幅图共有 30个点,第8幅图共有 72个点.
(2)第n幅图共有 n(n+1)个点.
三.判断题(满分8分,每小题2分)
17.第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
答案:√.
18.1+4+6+8+10+12+14=55
55>45
所以第7个点阵有45个点的说法是错误的;
答案:×.
19.①11×11=121
②111×111=12321
③1111×1111=1234321
④11111×11111=123454321
根据规律,原题计算正确.
答案:√.
20.在1+3+5+7+9+…中,从“1”到数“13”的项数为:(13﹣1)÷2+1=12÷2+1=6+1=721世纪教育网版权所有
前6项的和为:(13+1)×=14×3.5=49
因此,在1+3+5+7+9+…中,从“1”到数“13”的和是49,原题的说法是正确的.
答案:√.
四.计算题(满分24分,每小题6分)
21.答案:
22.(1)98×9=882
987×9=8883
9876×9=88884
98765×9=888885
(2)12×8+2=98
123×8+3=987
1234×8+4=9876
12345×8+5=98765
答案:882,8883,88884,888885;98,987,9876,98765.
23.答案:2.
9﹣3﹣4=2
答:应该填2.
如图:
24.第一张餐桌上可以摆放8把椅子,
进一步观察发现:多一张餐桌,多放4把椅子.
所以第n张餐桌共有4+4n把椅子,
(1)当n=8时,
4+4×8=36(人),
答:摆8张餐桌可以坐36人.
(2)当52人用餐时,
则,4+4n=52
4n=48
n=12
答:52人用餐,需要摆12张餐桌.
五.应用题(满分24分,每小题12分)
25.(1)拼1个五边形,需要小棒根数:5根
拼2个五边形,需要小棒根数:5+4=9(根)
拼3个五边形,需要小棒根数:5+4+4=13(根)
……
有拼n个五边形,需要小棒根数:5+4×(n﹣1)=(4n+1)(根)
当n=5时,所需小棒根数:
4×5+1
=20+1
=21(根)
答:拼成5个这样的五边形,一共要用 21根小棒.
(2)解:设一共拼成了x个五边形.
4x+1=57
4x=56
x=14
答:一共拼成了14个五边形.
答案:21.
26.(1)3+21+23+25+43=115
23×5=115
所以每次框出的5个数的和都是中间数的5倍;
(2)255÷5=51
所框的5个数里中间数是51,其余4个数是31,49,53,71;
(3)不能,200÷5=40,
因为40是偶数,奇数表中没有偶数,
所以不能在奇数表中框出和是200的5个数;
(4)根据所给框的例子,知道23、25、27、29、31、33、35、37、及它们对应的下两行的数,都可以被框为中间的数,21教育网
所以,一共可以框出大小不同的和的个数:8×3=24(个);
答:一共可以框出24个大小不同的和.
六.操作题(满分12分,每小题6分)
27.根据分析,作图如下:
28.(1)答案如下图:
(2)1+2+3+4+5+6+7+8+9+10=55
答:第10个数是55.
_21?????????è?????(www.21cnjy.com)_
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(二)卷
一.选择题(满分16分,每小题2分)
1.如图,按这样的规律第7个图形有( )个点.
A.21 B.25 C.28 D.29
2.根据1÷11=0.,2÷11=0.,3÷11=0.,可以推出9÷11=( )
A.0. B.0. C.0. D.0.
3.将一些小圆球如图摆放,第6幅图有( )个小圆球.
A.30 B.42 C.56
4.2×9=18,22×_99???217_8,222×999=221778,2222×9999=22217778,22222×99999=( )21cnjy.com
A.22117788 B.2222177778 C.222221778 D.2222177788
5.如图所示,在图_???1????????????_重叠的三角形共有4个,在图(2)中互不重叠的三角形共有7个,在图(3)中互不重叠的三角形共有10个,……,则在图(6)中,互不重叠的三角形共有( )21·cn·jy·com
A.10个 B.15个 C.19个 D.22个
6.填在如图各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A.38 B.52 C.66 D.74
7.用小棒按下面的规律摆三角形,摆n个三角形用( )根小棒.
A.2n+1 B.2(n﹣1) C.3+2n
8.寒假的时候,同学们去莲花山滑雪场滑雪,有些同学用雪杖摆成了如图:
像上面那样摆10个三角形,至少需要( )根滑雪杖.
A.21 B.20 C.9 D.30
二.填空题(满分16分,每小题2分)
9.计算得到11_1111?·3_7037=3,222222÷37037=6,333333÷37037=9,那么555555÷37037= .www.21-cn-jy.com
10.
照这样摆下去,摆10个正方形需要 根小棒,摆n个正方形,需要 根小棒.
11.找出下列算式的规律,并根据规律把算式填写完整.
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
×8+9=
12.如图所示,以一根火柴棍为一边,用火柴棍拼成一排由正方形组成的图形,如果图形中会用n个正方形,需要 根火柴棍.2·1·c·n·j·y
13.已知3÷11=0.2727…,4÷11=0.3636…,5÷11=0.4545…,照规律写一个算式和它的得数 = .【来源:21·世纪·教育·网】
14.玩搭积木游戏,每一阶段增多的积木的个数相同,所搭起来的积木的形状如下图所示.搭第8阶段一共需要积木 个.21·世纪*教育网
15.有一组算式如:4+2,5+8,6+14,7+20,……那么,第100个算式的得数是 .
16.仔细观察小黑点的排列,探索规律.
(1)第5幅图共有 个点,第8幅图共有 个点.
(2)第n幅图共有 个点.
三.判断题(满分8分,每小题2分)
17.如图,第五个点阵中点的个数是17个. (判断对错)
18.如图:
那么第7个点阵有45个点. .(判断对错)
19.找规律(不能用计算器计算_?????????11??_11=121,②111×111=12321,③1111×1111=1234321,那么④11111×11111=123454321. (判断对错)
20.在1+3+5+7+9+…中,从“1”到数“13”的和是49. .(判断对错)
四.计算题(满分24分,每小题6分)
21.(6分)找规律,填一填.
22.(6分)按规律填出下面算式的得数.
(1)98×9=
987×9=
9876×9=
9875×9=
(2)12×8+2=
123×8+3=
1234×8+4=
12345×8+5=
23.(6分)填一填.
24.(6分)按图摆放餐桌和椅子,摆8张餐桌可以坐多少人?52人用餐,需要摆多少张餐桌?
五.应用题(满分24分,每小题12分)
25.(12分)用小棒按下面的方式拼图形.
(1)如果按下面的规律拼成5个这样的五边形,一共要用 根小棒.
五边形
个数 拼成的形状 小棒根数
1
5
2
9
3
13
4
17
(2)接着拼下去,一共用了57根小棒,你知道一共拼成了多少个五边形吗?
26.(12分)表中一共有50个奇数,实线框出的5个数之和是115,仔细观察后回答问题.
(1)你能发现每次框出的5个数的和与中间数有什么关系?
(2)如果框出的5个数的和是255,应该怎样框?(用彩笔在图中框一框)
(3)能框出和是200的5个数吗?为什么?
(4)一共可以框出多少个大小不同的和?
六.操作题(满分12分,每小题6分)
27.(6分)找规律,画出表示“23”的图形.
28.(6分)(1)你根据下面图形与数的规律接着画一画,填一填.
(2)如果不画,这样排列下去,第10个数是多少?
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(二)卷
参考答案与试题解析
一.选择题(满分16分,每小题2分)
1.答案:B
第1个图形点数是1,
第2个图形点数是5,
第3个图形点数是9,则:
第4个图形点数是:9+4=13,
第5个图形点数是:13+4=17,
第6个图形点数是:17+4=21,
第7个图形点数是:21+4=25.
2.答案:D
根据题意与分析可得:
根据1÷11=0.,2÷11=0.,3÷11=0.,可以推出9÷11=0..
3.答案:B
观察图形可知:
第一个图形中有1×2=2个小圆球,
第二个图形中有2×3=6个小圆球,
第三个图形中有3×4=12个小圆球,
第四个图形中有4×5=20个小圆球,
…
所以第六幅图有6×7=42个小圆球.
4.答案:B
2×9=18
22×99=2178
222×999=221778
2222×9999=22217778
22222×99999=2222177778.
5.答案:C
在图(1)中互不重叠的三角形共有4个
在图(2)中互不重叠的三角形共有7个
在图(3)中互不重叠的三角形共有10个
……
在图n中互不重叠的三角形共4+3(n﹣1)=(3n+1)个
在图(6)中,互不重叠的三角形共有:
3×6+1
=18+1
=19(个)
答:在图(6)中,互不重叠的三角形共有19个。
6.答案:D
根据图形的规律,第4个图形:
左上数字为:2×4﹣2=6
左下应该是4×2=8
右上数字为:4×2+2=10
右下数字为:8×10﹣6=74
答:m的值是74.
7.答案:A
根据题干分析可得,当有n个三角形时小棒的数量就是:
3+2(n﹣1)
=3+2n﹣2
=2n+1(根)
答:摆n个三角形需要 2n+1根小棒.
8.答案:A
摆1个三角形,需要滑雪杖:3根
摆2个三角形,需要滑雪杖:3+2=5(根)
摆3个三角形,需要滑雪杖:3+2+2=7(根)
……
摆n个三角形,需要滑雪杖:3+2(n﹣1)=(2n+1)根
……
摆10个三角形需要滑雪杖:
2×10+1
=20+1
=21(根)
答:摆10个三角形,至少需要21根滑滑雪杖.
二.填空题(满分16分,每小题2分)
9.答案:15.
111111÷37037=3
222222÷37037=6
333333÷37037=9
……
商等于3乘被除数的每个数个位上的数的积
3×5=15
所以:555555÷37037=15
10.答案:40;4n。
根据题干分析可得:
摆一个正方形需要4根小棒,
摆两个正方形需要4×2=8根小棒,
摆三个正方形需要4×3=12根小棒,
…,
摆10个正方形需要10×4=40(根)
据此可得摆n个正方形需要4n根小棒,
答:摆10个正方形需要40根小棒,摆n个正方形,需要4n根小棒.
11.答案:见试题解答内容
1×8+1=9
12×8+2=98
123×8+3=987
1234×8+4=9876
……
123456789×8+9=987654321
12.答案:(3n+1)。
摆1个正方形需要火柴棍4根
摆2个正方形需要火柴棍4+3=7(根)
摆3个正方形需要火柴棍4+3+3=10(根)
……
摆n个正方形需要火柴棍4+3(n﹣1)=(3n+1)根
答:n个正方形,需要(3n+1)根火柴棍.
13.答案:9÷11;0.8181…(答案不唯一).
根据商的变化规律可知,
1÷11=0.0909…
2÷11=0.1818…
3÷11=0.2727…
4÷11=0.3636…
5÷11=0.4545…
6÷11=0.5454…
7÷11=0.6363…
8÷11=0.7272…
9÷11=0.8181…
14.答案:24.
根据题干分析可得:第n阶段,积木个数是3n;
当n=8时,3×8=24(个),
答:第8阶段有24个积木.
15.答案:699.
这组算式的规律是得数每次加7,
第1个算式得数是6,
第2个算式的得数是6+7=13,
第3个算式的得数是6+7×2=20,
第4个算式的得数是6+7×3=27,
……;
第100个算式的得数就是:
6+7×(100﹣1)=699
答:第100个算式的得数是 699.
16.答案:30;72;n(n+1).
第一幅图小黑点的个数为2个
第二幅图小黑点的个数:2+4=6(个)
第三幅图小黑点的个数为:2+4+6=12(个)
……
第n副图小黑点的个数为:2×(1+2+……+n)=n(n+1)个
(1)5×(5+1)
=5×6
=30(个)
8×(8+1)
=8×9
=72(个)
答:第5幅图共有 30个点,第8幅图共有 72个点.
(2)第n幅图共有 n(n+1)个点.
三.判断题(满分8分,每小题2分)
17.第一个点阵中点的个数:1个
第二个点阵中点的个数:1+4=5(个)
第三个点阵中点的个数:1+4+4=9(个)
……
第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)
……
第五个点阵中点的个数:
4×5﹣3
=20﹣3
=17(个)
答:第五个点阵中点的个数是17个.所以原说法正确.
答案:√.
18.1+4+6+8+10+12+14=55
55>45
所以第7个点阵有45个点的说法是错误的;
答案:×.
19.①11×11=121
②111×111=12321
③1111×1111=1234321
④11111×11111=123454321
根据规律,原题计算正确.
答案:√.
20.在1+3+5+7+9+…中,从“1”到数“13”的项数为:(13﹣1)÷2+1=12÷2+1=6+1=721世纪教育网版权所有
前6项的和为:(13+1)×=14×3.5=49
因此,在1+3+5+7+9+…中,从“1”到数“13”的和是49,原题的说法是正确的.
答案:√.
四.计算题(满分24分,每小题6分)
21.答案:
22.(1)98×9=882
987×9=8883
9876×9=88884
98765×9=888885
(2)12×8+2=98
123×8+3=987
1234×8+4=9876
12345×8+5=98765
答案:882,8883,88884,888885;98,987,9876,98765.
23.答案:2.
9﹣3﹣4=2
答:应该填2.
如图:
24.第一张餐桌上可以摆放8把椅子,
进一步观察发现:多一张餐桌,多放4把椅子.
所以第n张餐桌共有4+4n把椅子,
(1)当n=8时,
4+4×8=36(人),
答:摆8张餐桌可以坐36人.
(2)当52人用餐时,
则,4+4n=52
4n=48
n=12
答:52人用餐,需要摆12张餐桌.
五.应用题(满分24分,每小题12分)
25.(1)拼1个五边形,需要小棒根数:5根
拼2个五边形,需要小棒根数:5+4=9(根)
拼3个五边形,需要小棒根数:5+4+4=13(根)
……
有拼n个五边形,需要小棒根数:5+4×(n﹣1)=(4n+1)(根)
当n=5时,所需小棒根数:
4×5+1
=20+1
=21(根)
答:拼成5个这样的五边形,一共要用 21根小棒.
(2)解:设一共拼成了x个五边形.
4x+1=57
4x=56
x=14
答:一共拼成了14个五边形.
答案:21.
26.(1)3+21+23+25+43=115
23×5=115
所以每次框出的5个数的和都是中间数的5倍;
(2)255÷5=51
所框的5个数里中间数是51,其余4个数是31,49,53,71;
(3)不能,200÷5=40,
因为40是偶数,奇数表中没有偶数,
所以不能在奇数表中框出和是200的5个数;
(4)根据所给框的例子,知道23、25、27、29、31、33、35、37、及它们对应的下两行的数,都可以被框为中间的数,21教育网
所以,一共可以框出大小不同的和的个数:8×3=24(个);
答:一共可以框出24个大小不同的和.
六.操作题(满分12分,每小题6分)
27.根据分析,作图如下:
28.(1)答案如下图:
(2)1+2+3+4+5+6+7+8+9+10=55
答:第10个数是55.
_21?????????è?????(www.21cnjy.com)_
