人教版小学数学六年级上册第八单元数学广角--数与形单元检测(三)卷(含答案)
文档属性
| 名称 | 人教版小学数学六年级上册第八单元数学广角--数与形单元检测(三)卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 10:25:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(三)卷
一.选择题(满分16分,每小题2分)
1.观察下列等_??????21???2_,22=4,23=8,24=16,25=32,26=64,27=128,……通过观察,用你所发现的规律确定22019的个位数字是( )21教育网
A.2 B.4 C.6 D.8
2.已知:12345.679×9_???11111_1.111,12345.679×18=222222.222,12345.679×27=333333.333,则12345.679×63=( )www.21-cn-jy.com
A.444444.444 B.555555.555 C.666666.666 D.777777.777
3.根据下面三个算式找规律:1÷11=0.0909…;2÷11=0.1818…;3÷11=0.2727…;想一想,4÷11=( )【来源:21·世纪·教育·网】
A.0.4444… B.0.3636… C.0.4545… D.0.5454…
4.法国的“小九九”从“一一得_????????°?????????_二十五”和我国的“小九九”是一样的,后面的就改用手势了.如图两个图框是用法国“小九九”计算7×8和8×9的两个示例.若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是( )
A.2,3 B.3,3 C.2,4 D.3,4
5.如图是用棋子摆成的图形,摆_???????????????é??_要3枚棋子,摆第二个图形需要6枚棋子,摆第三个图形需要9枚棋子……照这样的规律摆第11个图形需要( )枚棋子.
A.27 B.30 C.33 D.36
6.用同样长的小棒摆出如下的图形.照这样继续摆,摆第6个图形用了( )根小棒.
A.20 B.25 C.24
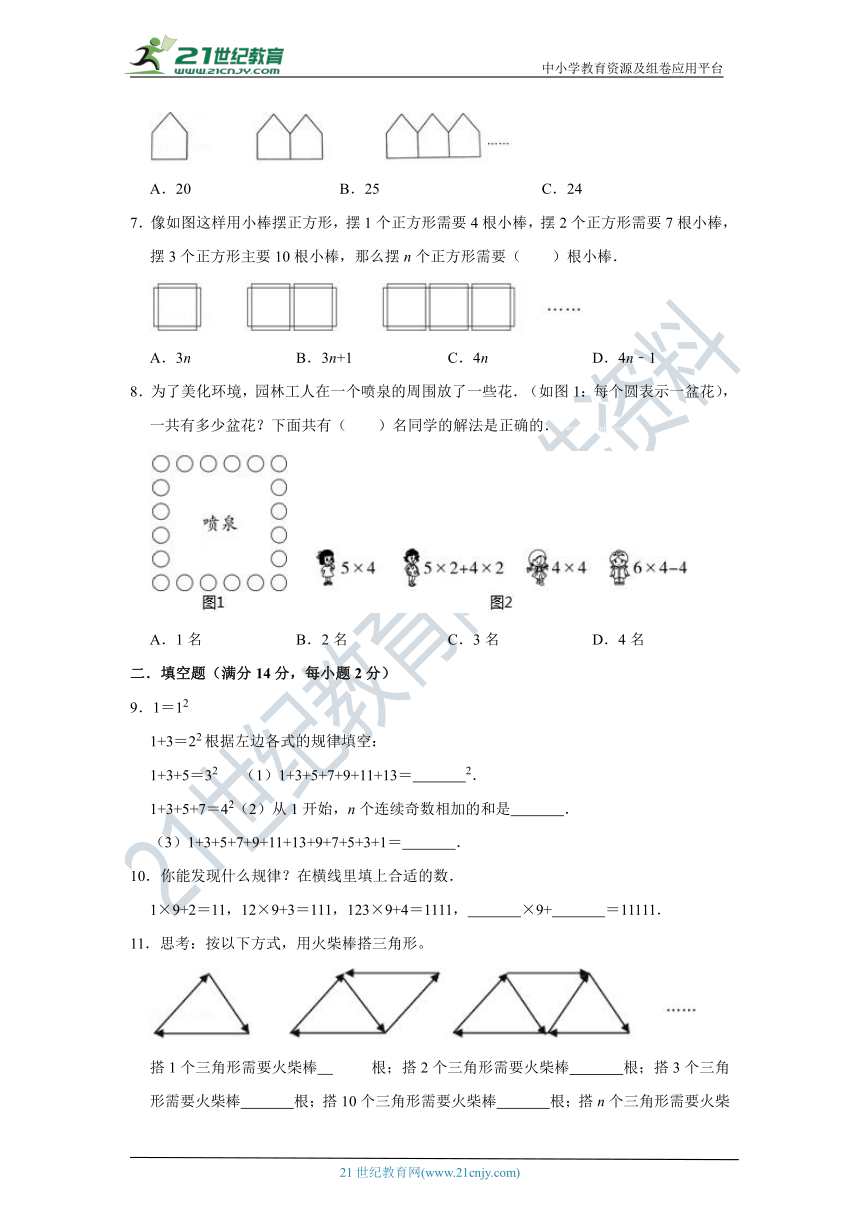
7.像如图这样用小棒摆正方形,_???1????????????_需要4根小棒,摆2个正方形需要7根小棒,摆3个正方形主要10根小棒,那么摆n个正方形需要( )根小棒.
A.3n B.3n+1 C.4n D.4n﹣1
8.为了美化环境,园林工人在一个喷泉的周围放了一些花.(如图1:每个圆表示一盆花),一共有多少盆花?下面共有( )名同学的解法是正确的.www-2-1-cnjy-com
A.1名 B.2名 C.3名 D.4名
二.填空题(满分14分,每小题2分)
9.1=12
1+3=22根据左边各式的规律填空:
1+3+5=32 (1)1+3+5+7+9+11+13= 2.
1+3+5+7=42(2)从1开始,n个连续奇数相加的和是 .
(3)1+3+5+7+9+11+13+9+7+5+3+1= .
10.你能发现什么规律?在横线里填上合适的数.
1×9+2=11,12×9+3=111,123×9+4=1111, ×9+ =11111.
11.思考:按以下方式,用火柴棒搭三角形。
搭1个三角形需要火柴棒 ____?????????_搭2个三角形需要火柴棒 根;搭3个三角形需要火柴棒 根;搭10个三角形需要火柴棒 根;搭n个三角形需要火柴棒 根.21*cnjy*com
12.找规律填数。
(1)9.7、8.6、7.5、 、5.3、 。
(2)2.7、3.3、 4.5、5.1、 。
13.根据规律填空.
1÷9=0.1111…
2÷9=0.2222…
3÷9=0.3333…
4÷9=
5÷9=
14.找规律,写得数.
=1,=,=
据上面等式,则:=
15.照如图的规律画下去,第5个图形中有白色的正方形 个,灰色的正方形 个.
三.判断题(满分8分,每小题2分)
16.(6分),,,,,,……这列数每一项越来越小,越来越接近0. (判断对错)2-1-c-n-j-y
17.(6分)3×4=1_2???33??3_4=1122,333×334=111222根据前三题的得数,33333×33334=11112222. (判断对错)【来源:21cnj*y.co*m】
18.(6分)…,第五个点阵中点的个数是1+4×5=21. .(判断对错)
19.(6分)用小木棒照下图搭正方形,搭一个用4根,搭两个用7根,搭a个用4a根. (判断对错)【出处:21教育名师】
四.计算题(满分24分)
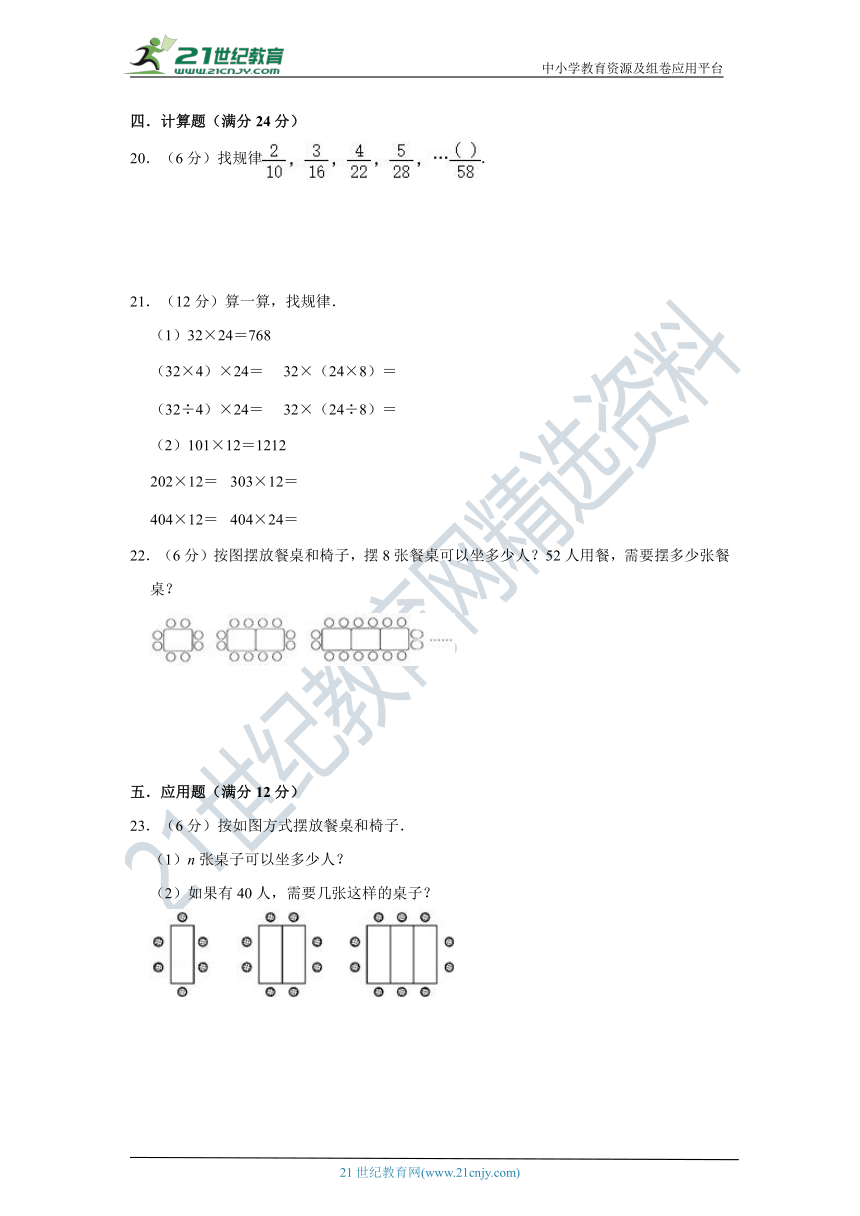
20.(6分)找规律.
21.(12分)算一算,找规律.
(1)32×24=768
(32×4)×24= 32×(24×8)=
(32÷4)×24= 32×(24÷8)=
(2)101×12=1212
202×12= 303×12=
404×12= 404×24=
22.(6分)按图摆放餐桌和椅子,摆8张餐桌可以坐多少人?52人用餐,需要摆多少张餐桌?
五.应用题(满分12分)
23.(6分)按如图方式摆放餐桌和椅子.
(1)n张桌子可以坐多少人?
(2)如果有40人,需要几张这样的桌子?
24.(6分)有一列数:,,,,,,,…它的前2015个数的和是多少?
六.操作题(满分12分)
25.(6分)照样子,在叶片上填写数.
26.(6分)观察点阵中的规律,请画出所缺图.?
七.解答题(满分14分)
27.(7分)如图是边长为1cm的正方形ABCD,沿水平方向翻滚4次后的位置图形,此时A翻滚后所在的位置与A点开始位置之间的距离为4厘米.21·世纪*教育网
请你根据图形,完成下表:(此题只加分不扣分)
翻滚次数 4 15 16 4n﹣1 4n
与A点开始位置之间(厘米) 4
28.(7分)12和60是很有趣的两个数,这两个数的积恰好是这两个数的和的10倍:12×60=720,12+60=72.【版权所有:21教育】
满足这个条件的正整数还有哪些?
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(三)卷
参考答案与试题解析
一.选择题
1.以2为底的幂的末位数字是2,4,8,6…依次循环的,
2019÷4=504…3,
所以22019的个位数字是8.
答案:D.
2.根据题干分析可得:
12345.679×9=111111.111
12345.679×18=222222.222
12345.679×27=333333.333
则12345.679×63=777777.777
答案:D.
3.根据规律可知:
4÷11=0.3636…
答案:B.
4.要计算7×9,左手应伸出手指:
7﹣5=2(个);
右手应伸出手指:
9﹣5=4(个);
答案:C.
5.根据题干分析可得:摆第一个图形需要3=3×1枚棋子,
摆第二个图形需要3×2=6枚棋子,
摆第三个图形需要3×3=9枚棋子,
摆第四个图形需要3×4=12枚棋子
…,
据此可得摆第n个图形需要3n枚棋子,
当n=11时,11×3=33(枚)
答:照这样的规律摆第11个图形需要33枚棋子.
答案:C.
6.由图可知:
图形1的小棒根数为5;
图形2的小棒根数为9;
图形3的小棒根数为13;
…
由该搭建方式可得出规律:图形标号每增加1,小棒的个数增加4,
所以可以得出规律:第n个图形需要小棒5+4(n﹣1)=4n+1根,
当n=6时,需要小棒:4×6+1=25(根)
答:摆第6个图形用了25根小棒.
答案:B.
7.摆1个正方形需要4根小棒
摆2个正方形需要7根小棒
摆3个正方形主要10根小棒
……摆n个正方形需要小棒:
4+(n﹣1)×3
=4+3n﹣3
=(3n+1)根
答:摆n个正方形需要(3n+1)根小棒.
答案:B.
8.根据题干分析可得,花盆的总数为:6×4﹣4=20(盆)
或者5×4=20(盆)
有两个小朋友算对了.
答案:B.
二.填空题
9.(1)1+3+5+7+9+11+13=72
(2)从1开始,n个连续奇数相加的和是n2
(3)1+3+5+7+9+11+13+9+7+5+3+1
=72+52
=49+25
=74
答案:7,n2,74.
10.1×9+2=11,12×9+3=111,123×9+4=1111,1234×9+5=11111;
答案:1234、5.
11.搭1个三角形需要火柴棒3根
搭2个三角形需要火柴棒5根
搭3个三角形需要火柴棒7根
搭10个三角形需要火柴棒21根
搭n个三角形需要火柴棒(2n+1)根
所以,10个三角形即n=10,
2×10+1=21(根)
答:搭1个三角_???é??è???????????_3根;搭2个三角形需要火柴棒5根;搭3个三角形需要火柴棒7根;搭10个三角形需要火柴棒21根;搭n个三角形需要火柴棒(2n+1)根。
答案:3;5;7;21;2n+1。
12.9.7﹣8.6=1.1,8.6﹣7.5=1.1
7.5﹣1.1=6.4
5.3﹣1.1=4.2
9.7、8.6、7.5、6.4、5.3、4.2。
(2)3.3﹣2.7=0.6…5.1﹣4.5=0.6
3.3+0.6=3.9
5.1+0.6=5.7
2.7、3.3、3.9、4.5、5.1、5.7。
答案:6.4,4.2;3.9,5.7。
13.1÷9=0.1111…
2÷9=0.2222…
3÷9=0.3333…
4÷9=0.4444…
5÷9=0.5555…
答案:0.4444…;0.5555…
14.+
=++++
=1﹣+﹣+﹣+﹣+﹣
=1﹣
=
答案:.
15.根据题干分析可得,第一个图形中白色的正方形是12=1(个),灰色的正方形是32﹣12=8(个)21世纪教育网版权所有
第二个图形中白色的正方形是22=4(个),灰色的正方形是42﹣22=12(个)
第三个图形中白色正方形是32=9(个),灰色正方形的个数是52﹣32=16(个)
……,由此可得
第5个图形中白色的正方形是52=25(个),黑色的正方形是72﹣52=24(个)
答:第5个图形中有白色的正方形 25个,灰色的正方形 24个.
答案:25;24.
三.判断题
16.这列分数分子都是1,且分母依次乘2,分母无限大,则分数值无限小,越来越接近0,所以原题说法正确.21cnjy.com
答案:√.
17.根据分析可得:
33333×33334=1111122222;
所以,原题说法错误.
答案:×.
18.根据题干分析可得:第n点阵的点数=1+(n﹣1)×4,
n=5时,点数个数为:1+(5﹣1)×4=17.
所以原题说法错误.
答案:错误.
19.摆1个正方形,需要4根火柴,可以写成1×3+1;
摆2个正方形,需要7根火柴,可以写成2×3+1;
摆3个正方形,需要10根火柴,可以写成3×3+1;
…
所以第a个正方形,需要3a+1根火柴,
答案:×.
四.计算题
20.(58﹣10)÷6,
=48÷6,
=8;
所以是这个数列的第9项,它的分子就是10.
即这个分数是.
答案:10.
21.(1)32×24=768
(32×4)×24=3072 32×(24×8)=6144
(32÷4)×24=192 32×(24÷8)=96
(2)101×12=1212
202×12=2424 303×12=3636
404×12=4848 404×24=9696
22.第一张餐桌上可以摆放8把椅子,
进一步观察发现:多一张餐桌,多放4把椅子.
所以第n张餐桌共有4+4n把椅子,
(1)当n=8时,
4+4×8=36(人),
答:摆8张餐桌可以坐36人.
(2)当52人用餐时,
则,4+4n=52
4n=48
n=12
答:52人用餐,需要摆12张餐桌.
五.应用题
23.(1)观察图形可知:
一张餐桌可摆放4+2×1=6把椅子,可以坐6人;
两张餐桌可摆放4+2×2=8把椅子,可以坐8人;
三张餐桌可摆放4+2×3=10把椅子,可以坐10人;
所以n张餐桌可摆放4+2n把椅子,可以坐(4+2n)人;
答:n张桌子可以坐(4+2n)人.
(2)解:设需要x张这样的桌子.
2x+4=40
2x+4﹣4=40﹣4
2x=36
2x÷2=36÷2
x=18
答:需要18张这样的桌子.
24.以1为分母的数有1个,相加和S1=1,
以2为分母的数有2个,相加和S2=+=,
以3为分母的数有3个,相加和S3=++=2,…
以n为分母的数有n个,相加和Sn=++…+==,
求前2015个数的和,先确定第2015个数分母是什么,即求满足 1+2+3+4…+m=≥2015的最小整数n,易得n=63,62×63÷2=1953,21·cn·jy·com
分母为63的数有2015﹣1953=62个,即、、、…、,
则前2015个数的和是:
S=S1+S2+…S62++++…+
=(1+2+3+…62)÷2+(1+2+3+…+62)÷63
=(1+62)×62÷2÷2+(1+62)×62÷2÷63
=976.5+31
=1007.5
答:它的前2015个数的和是1007.5.
六.操作题
25.
26.通过图案观察可知,当n=5时,就有5行,点的个数是:1+3+5+7+9=52=25(个)
据此画图如下:
七.解答题
27.
翻滚次数 4 15 16 4n﹣1 4n
与A点开始位置之间(厘米) 4 15 16 4n﹣1 4n
28.设满足条件的正整数对是a和b(a≥b),根据题意,得:
ab=10(a+b),
?ab=10a+10b,
?ab﹣10a=10b,
?a(b﹣10)=10b,
?a﹣==10+.
因为a是正整数,所以b是大_???10?????????_数,并且(b﹣10)是100的约束,推出b=11,12,14,15,20;相应地得到a=110,60,35,30,20.即正整数对还有(11,110)、(14,35)、(15,30)、(20,20).2·1·c·n·j·y
_21?????????è?????(www.21cnjy.com)_
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(三)卷
一.选择题(满分16分,每小题2分)
1.观察下列等_??????21???2_,22=4,23=8,24=16,25=32,26=64,27=128,……通过观察,用你所发现的规律确定22019的个位数字是( )21教育网
A.2 B.4 C.6 D.8
2.已知:12345.679×9_???11111_1.111,12345.679×18=222222.222,12345.679×27=333333.333,则12345.679×63=( )www.21-cn-jy.com
A.444444.444 B.555555.555 C.666666.666 D.777777.777
3.根据下面三个算式找规律:1÷11=0.0909…;2÷11=0.1818…;3÷11=0.2727…;想一想,4÷11=( )【来源:21·世纪·教育·网】
A.0.4444… B.0.3636… C.0.4545… D.0.5454…
4.法国的“小九九”从“一一得_????????°?????????_二十五”和我国的“小九九”是一样的,后面的就改用手势了.如图两个图框是用法国“小九九”计算7×8和8×9的两个示例.若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是( )
A.2,3 B.3,3 C.2,4 D.3,4
5.如图是用棋子摆成的图形,摆_???????????????é??_要3枚棋子,摆第二个图形需要6枚棋子,摆第三个图形需要9枚棋子……照这样的规律摆第11个图形需要( )枚棋子.
A.27 B.30 C.33 D.36
6.用同样长的小棒摆出如下的图形.照这样继续摆,摆第6个图形用了( )根小棒.
A.20 B.25 C.24
7.像如图这样用小棒摆正方形,_???1????????????_需要4根小棒,摆2个正方形需要7根小棒,摆3个正方形主要10根小棒,那么摆n个正方形需要( )根小棒.
A.3n B.3n+1 C.4n D.4n﹣1
8.为了美化环境,园林工人在一个喷泉的周围放了一些花.(如图1:每个圆表示一盆花),一共有多少盆花?下面共有( )名同学的解法是正确的.www-2-1-cnjy-com
A.1名 B.2名 C.3名 D.4名
二.填空题(满分14分,每小题2分)
9.1=12
1+3=22根据左边各式的规律填空:
1+3+5=32 (1)1+3+5+7+9+11+13= 2.
1+3+5+7=42(2)从1开始,n个连续奇数相加的和是 .
(3)1+3+5+7+9+11+13+9+7+5+3+1= .
10.你能发现什么规律?在横线里填上合适的数.
1×9+2=11,12×9+3=111,123×9+4=1111, ×9+ =11111.
11.思考:按以下方式,用火柴棒搭三角形。
搭1个三角形需要火柴棒 ____?????????_搭2个三角形需要火柴棒 根;搭3个三角形需要火柴棒 根;搭10个三角形需要火柴棒 根;搭n个三角形需要火柴棒 根.21*cnjy*com
12.找规律填数。
(1)9.7、8.6、7.5、 、5.3、 。
(2)2.7、3.3、 4.5、5.1、 。
13.根据规律填空.
1÷9=0.1111…
2÷9=0.2222…
3÷9=0.3333…
4÷9=
5÷9=
14.找规律,写得数.
=1,=,=
据上面等式,则:=
15.照如图的规律画下去,第5个图形中有白色的正方形 个,灰色的正方形 个.
三.判断题(满分8分,每小题2分)
16.(6分),,,,,,……这列数每一项越来越小,越来越接近0. (判断对错)2-1-c-n-j-y
17.(6分)3×4=1_2???33??3_4=1122,333×334=111222根据前三题的得数,33333×33334=11112222. (判断对错)【来源:21cnj*y.co*m】
18.(6分)…,第五个点阵中点的个数是1+4×5=21. .(判断对错)
19.(6分)用小木棒照下图搭正方形,搭一个用4根,搭两个用7根,搭a个用4a根. (判断对错)【出处:21教育名师】
四.计算题(满分24分)
20.(6分)找规律.
21.(12分)算一算,找规律.
(1)32×24=768
(32×4)×24= 32×(24×8)=
(32÷4)×24= 32×(24÷8)=
(2)101×12=1212
202×12= 303×12=
404×12= 404×24=
22.(6分)按图摆放餐桌和椅子,摆8张餐桌可以坐多少人?52人用餐,需要摆多少张餐桌?
五.应用题(满分12分)
23.(6分)按如图方式摆放餐桌和椅子.
(1)n张桌子可以坐多少人?
(2)如果有40人,需要几张这样的桌子?
24.(6分)有一列数:,,,,,,,…它的前2015个数的和是多少?
六.操作题(满分12分)
25.(6分)照样子,在叶片上填写数.
26.(6分)观察点阵中的规律,请画出所缺图.?
七.解答题(满分14分)
27.(7分)如图是边长为1cm的正方形ABCD,沿水平方向翻滚4次后的位置图形,此时A翻滚后所在的位置与A点开始位置之间的距离为4厘米.21·世纪*教育网
请你根据图形,完成下表:(此题只加分不扣分)
翻滚次数 4 15 16 4n﹣1 4n
与A点开始位置之间(厘米) 4
28.(7分)12和60是很有趣的两个数,这两个数的积恰好是这两个数的和的10倍:12×60=720,12+60=72.【版权所有:21教育】
满足这个条件的正整数还有哪些?
人教版小学数学六年级上册第八单元数学广角--数与形单元检测(三)卷
参考答案与试题解析
一.选择题
1.以2为底的幂的末位数字是2,4,8,6…依次循环的,
2019÷4=504…3,
所以22019的个位数字是8.
答案:D.
2.根据题干分析可得:
12345.679×9=111111.111
12345.679×18=222222.222
12345.679×27=333333.333
则12345.679×63=777777.777
答案:D.
3.根据规律可知:
4÷11=0.3636…
答案:B.
4.要计算7×9,左手应伸出手指:
7﹣5=2(个);
右手应伸出手指:
9﹣5=4(个);
答案:C.
5.根据题干分析可得:摆第一个图形需要3=3×1枚棋子,
摆第二个图形需要3×2=6枚棋子,
摆第三个图形需要3×3=9枚棋子,
摆第四个图形需要3×4=12枚棋子
…,
据此可得摆第n个图形需要3n枚棋子,
当n=11时,11×3=33(枚)
答:照这样的规律摆第11个图形需要33枚棋子.
答案:C.
6.由图可知:
图形1的小棒根数为5;
图形2的小棒根数为9;
图形3的小棒根数为13;
…
由该搭建方式可得出规律:图形标号每增加1,小棒的个数增加4,
所以可以得出规律:第n个图形需要小棒5+4(n﹣1)=4n+1根,
当n=6时,需要小棒:4×6+1=25(根)
答:摆第6个图形用了25根小棒.
答案:B.
7.摆1个正方形需要4根小棒
摆2个正方形需要7根小棒
摆3个正方形主要10根小棒
……摆n个正方形需要小棒:
4+(n﹣1)×3
=4+3n﹣3
=(3n+1)根
答:摆n个正方形需要(3n+1)根小棒.
答案:B.
8.根据题干分析可得,花盆的总数为:6×4﹣4=20(盆)
或者5×4=20(盆)
有两个小朋友算对了.
答案:B.
二.填空题
9.(1)1+3+5+7+9+11+13=72
(2)从1开始,n个连续奇数相加的和是n2
(3)1+3+5+7+9+11+13+9+7+5+3+1
=72+52
=49+25
=74
答案:7,n2,74.
10.1×9+2=11,12×9+3=111,123×9+4=1111,1234×9+5=11111;
答案:1234、5.
11.搭1个三角形需要火柴棒3根
搭2个三角形需要火柴棒5根
搭3个三角形需要火柴棒7根
搭10个三角形需要火柴棒21根
搭n个三角形需要火柴棒(2n+1)根
所以,10个三角形即n=10,
2×10+1=21(根)
答:搭1个三角_???é??è???????????_3根;搭2个三角形需要火柴棒5根;搭3个三角形需要火柴棒7根;搭10个三角形需要火柴棒21根;搭n个三角形需要火柴棒(2n+1)根。
答案:3;5;7;21;2n+1。
12.9.7﹣8.6=1.1,8.6﹣7.5=1.1
7.5﹣1.1=6.4
5.3﹣1.1=4.2
9.7、8.6、7.5、6.4、5.3、4.2。
(2)3.3﹣2.7=0.6…5.1﹣4.5=0.6
3.3+0.6=3.9
5.1+0.6=5.7
2.7、3.3、3.9、4.5、5.1、5.7。
答案:6.4,4.2;3.9,5.7。
13.1÷9=0.1111…
2÷9=0.2222…
3÷9=0.3333…
4÷9=0.4444…
5÷9=0.5555…
答案:0.4444…;0.5555…
14.+
=++++
=1﹣+﹣+﹣+﹣+﹣
=1﹣
=
答案:.
15.根据题干分析可得,第一个图形中白色的正方形是12=1(个),灰色的正方形是32﹣12=8(个)21世纪教育网版权所有
第二个图形中白色的正方形是22=4(个),灰色的正方形是42﹣22=12(个)
第三个图形中白色正方形是32=9(个),灰色正方形的个数是52﹣32=16(个)
……,由此可得
第5个图形中白色的正方形是52=25(个),黑色的正方形是72﹣52=24(个)
答:第5个图形中有白色的正方形 25个,灰色的正方形 24个.
答案:25;24.
三.判断题
16.这列分数分子都是1,且分母依次乘2,分母无限大,则分数值无限小,越来越接近0,所以原题说法正确.21cnjy.com
答案:√.
17.根据分析可得:
33333×33334=1111122222;
所以,原题说法错误.
答案:×.
18.根据题干分析可得:第n点阵的点数=1+(n﹣1)×4,
n=5时,点数个数为:1+(5﹣1)×4=17.
所以原题说法错误.
答案:错误.
19.摆1个正方形,需要4根火柴,可以写成1×3+1;
摆2个正方形,需要7根火柴,可以写成2×3+1;
摆3个正方形,需要10根火柴,可以写成3×3+1;
…
所以第a个正方形,需要3a+1根火柴,
答案:×.
四.计算题
20.(58﹣10)÷6,
=48÷6,
=8;
所以是这个数列的第9项,它的分子就是10.
即这个分数是.
答案:10.
21.(1)32×24=768
(32×4)×24=3072 32×(24×8)=6144
(32÷4)×24=192 32×(24÷8)=96
(2)101×12=1212
202×12=2424 303×12=3636
404×12=4848 404×24=9696
22.第一张餐桌上可以摆放8把椅子,
进一步观察发现:多一张餐桌,多放4把椅子.
所以第n张餐桌共有4+4n把椅子,
(1)当n=8时,
4+4×8=36(人),
答:摆8张餐桌可以坐36人.
(2)当52人用餐时,
则,4+4n=52
4n=48
n=12
答:52人用餐,需要摆12张餐桌.
五.应用题
23.(1)观察图形可知:
一张餐桌可摆放4+2×1=6把椅子,可以坐6人;
两张餐桌可摆放4+2×2=8把椅子,可以坐8人;
三张餐桌可摆放4+2×3=10把椅子,可以坐10人;
所以n张餐桌可摆放4+2n把椅子,可以坐(4+2n)人;
答:n张桌子可以坐(4+2n)人.
(2)解:设需要x张这样的桌子.
2x+4=40
2x+4﹣4=40﹣4
2x=36
2x÷2=36÷2
x=18
答:需要18张这样的桌子.
24.以1为分母的数有1个,相加和S1=1,
以2为分母的数有2个,相加和S2=+=,
以3为分母的数有3个,相加和S3=++=2,…
以n为分母的数有n个,相加和Sn=++…+==,
求前2015个数的和,先确定第2015个数分母是什么,即求满足 1+2+3+4…+m=≥2015的最小整数n,易得n=63,62×63÷2=1953,21·cn·jy·com
分母为63的数有2015﹣1953=62个,即、、、…、,
则前2015个数的和是:
S=S1+S2+…S62++++…+
=(1+2+3+…62)÷2+(1+2+3+…+62)÷63
=(1+62)×62÷2÷2+(1+62)×62÷2÷63
=976.5+31
=1007.5
答:它的前2015个数的和是1007.5.
六.操作题
25.
26.通过图案观察可知,当n=5时,就有5行,点的个数是:1+3+5+7+9=52=25(个)
据此画图如下:
七.解答题
27.
翻滚次数 4 15 16 4n﹣1 4n
与A点开始位置之间(厘米) 4 15 16 4n﹣1 4n
28.设满足条件的正整数对是a和b(a≥b),根据题意,得:
ab=10(a+b),
?ab=10a+10b,
?ab﹣10a=10b,
?a(b﹣10)=10b,
?a﹣==10+.
因为a是正整数,所以b是大_???10?????????_数,并且(b﹣10)是100的约束,推出b=11,12,14,15,20;相应地得到a=110,60,35,30,20.即正整数对还有(11,110)、(14,35)、(15,30)、(20,20).2·1·c·n·j·y
_21?????????è?????(www.21cnjy.com)_
