五年级上册数学课件-5.1平行四边形的面积 西师大版 (共22张PPT)
文档属性
| 名称 | 五年级上册数学课件-5.1平行四边形的面积 西师大版 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 890.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览






文档简介
第5单元 多边形面积的计算
1 平行四边形的面积
学习目标
1.掌握平行四边形的面积公式。
2.理解平行四边形的面积公式的推导过程。
长方形面积=长×宽
复习导入
你还记得长方形的面积公式吗?
情景导入1
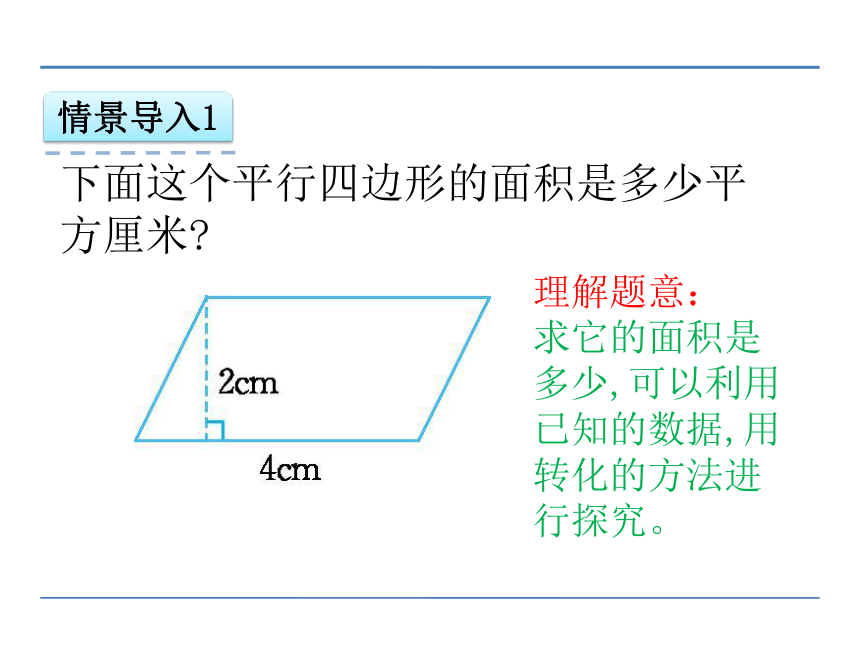
下面这个平行四边形的面积是多少平方厘米?
理解题意:
求它的面积是多少,可以利用已知的数据,用转化的方法进行探究。
探究新知
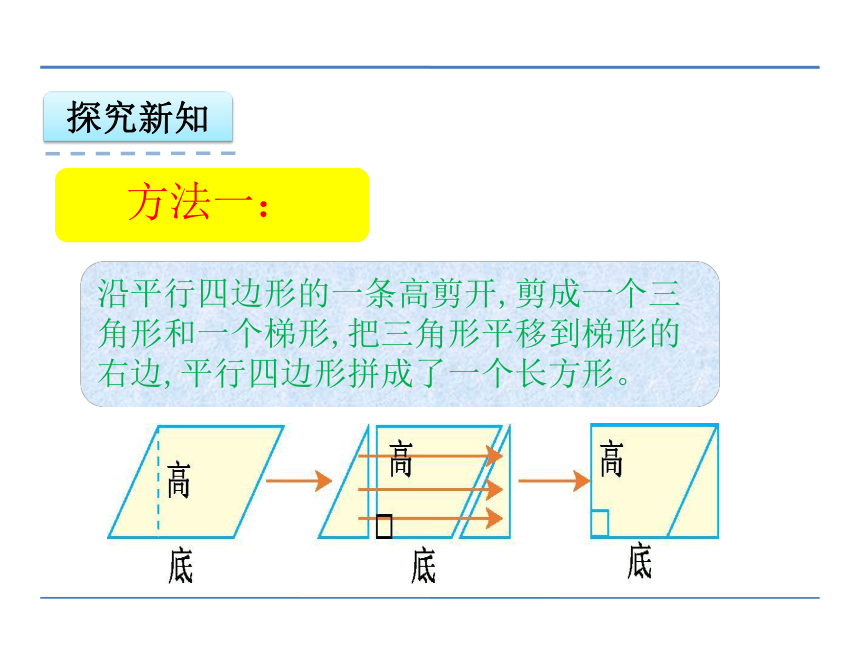
方法一:
沿平行四边形的一条高剪开,剪成一个三角形和一个梯形,把三角形平移到梯形的右边,平行四边形拼成了一个长方形。
探究新知
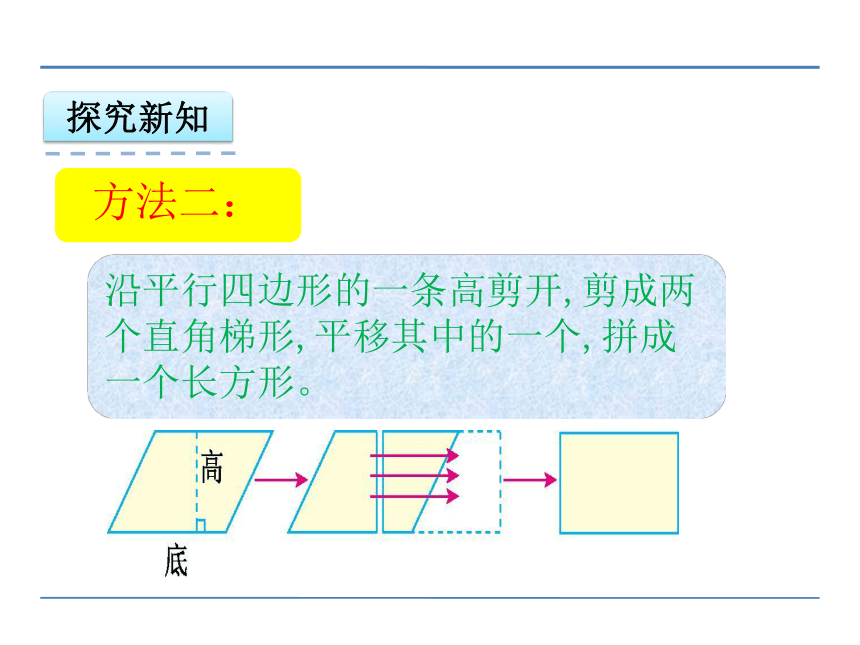
方法二:
沿平行四边形的一条高剪开,剪成两个直角梯形,平移其中的一个,拼成一个长方形。
探究新知
方法三:
拼出的长方形的面积与原来的平行四边形的面积相等,长方形的长与平行四边形的底相等,长方形的宽与平行四边形的高相等。
探究新知
解决问题:
解:
用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么平行四边形的面积公式可写成S=ah。
4×2=8(平方厘米)
这个平行四边形的面积是8平方厘米。
答:
知道了其中任意两个量,都可以求出第三个量:S=ah、a=S÷h、h=S÷a。
情景导入2
方格纸上平行四边形的面积分别是多少?(每个方格表示1cm2)
理解题意:
每个方格表示1cm2,那么每个方格的边长是1cm。
探究新知
方法:
计算平行四边形的面积时,底和高必须是相对应的。由此可知,图①的底是2cm,高是3cm;图②的底是6cm,高是2cm。把已知的数代入公式中。
探究新知
解决问题:
解:
①2×3=6(cm2) ②6×2=12(cm2)
答:
图①的面积是6cm2,
图②的面积是12cm2。
典题精讲
解题思路:
1. 判断:把一个长方形的木条框拉成一个平行四边形,面积和周长不变。 ( )
把长方形的木条拉成平行四边形,底不变,高变小了。所以周长不变,面积变小。
解答:
( ? )
典题精讲
2.计算下面平行四边形的面积。
利用平行四边形面积公式计算。
S=ah
=4×2.5
=10(cm2)
解答:
解答思路:
易错提醒
错误原因:周长相等的两个平行四边形,它们的底和高不一定相等,所以面积也就不一定相等。
判断:周长相等的两个平行四边形的面积也相等。 ( )
错误解答: ( √ )
错误解答
课件PPT
正确解答:(?)
两个平行四边形的面积是否相等,应根据底和高的情况来判断。
易错提醒
正确解答
解:
学以致用
1.
找到平行四边形高所在的底。
计算下面平行四边形的面积。
S=ah
=12×10
=120(cm2)
课件PPT
?
解:
学以致用
2.
前提是底高相等的长方形和平行四边形。
判断:长方形的面积等于平行四边形的面积。 ( )
课件PPT
11.2÷5=2.24(cm)
解:
学以致用
3.
根据a=S÷h
已知一个平行四边形的一条高是5cm,面积是11.2cm2,求平行四边形这条高所对应的底边长。
底边长为2.24cm。
答:
课件PPT
课件PPT
4.判断:平行四边形只有一条高。 ( )
平行四边形有无数条高。
学以致用
解:
(?)
课件PPT
5.判断:平行四边形有一条边是10cm,有一条高是8cm,则该平行四边形面积一定是80cm2。 ( )
给出的边和高不一定是对应的底和高。
学以致用
解:
(?)
课堂小结
平行四边形面积怎样计算?
求平行四边形面积应注意什么?
1.长方形的长=平行四边形的底,长方形的宽=平行四边形的高。
3.应用公式计算平行四边形的面积时,底和高必须是对应的。
2.平行四边形的面积公式:S=ah、a=S÷h、h=S÷a。
谢谢
1 平行四边形的面积
学习目标
1.掌握平行四边形的面积公式。
2.理解平行四边形的面积公式的推导过程。
长方形面积=长×宽
复习导入
你还记得长方形的面积公式吗?
情景导入1
下面这个平行四边形的面积是多少平方厘米?
理解题意:
求它的面积是多少,可以利用已知的数据,用转化的方法进行探究。
探究新知
方法一:
沿平行四边形的一条高剪开,剪成一个三角形和一个梯形,把三角形平移到梯形的右边,平行四边形拼成了一个长方形。
探究新知
方法二:
沿平行四边形的一条高剪开,剪成两个直角梯形,平移其中的一个,拼成一个长方形。
探究新知
方法三:
拼出的长方形的面积与原来的平行四边形的面积相等,长方形的长与平行四边形的底相等,长方形的宽与平行四边形的高相等。
探究新知
解决问题:
解:
用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么平行四边形的面积公式可写成S=ah。
4×2=8(平方厘米)
这个平行四边形的面积是8平方厘米。
答:
知道了其中任意两个量,都可以求出第三个量:S=ah、a=S÷h、h=S÷a。
情景导入2
方格纸上平行四边形的面积分别是多少?(每个方格表示1cm2)
理解题意:
每个方格表示1cm2,那么每个方格的边长是1cm。
探究新知
方法:
计算平行四边形的面积时,底和高必须是相对应的。由此可知,图①的底是2cm,高是3cm;图②的底是6cm,高是2cm。把已知的数代入公式中。
探究新知
解决问题:
解:
①2×3=6(cm2) ②6×2=12(cm2)
答:
图①的面积是6cm2,
图②的面积是12cm2。
典题精讲
解题思路:
1. 判断:把一个长方形的木条框拉成一个平行四边形,面积和周长不变。 ( )
把长方形的木条拉成平行四边形,底不变,高变小了。所以周长不变,面积变小。
解答:
( ? )
典题精讲
2.计算下面平行四边形的面积。
利用平行四边形面积公式计算。
S=ah
=4×2.5
=10(cm2)
解答:
解答思路:
易错提醒
错误原因:周长相等的两个平行四边形,它们的底和高不一定相等,所以面积也就不一定相等。
判断:周长相等的两个平行四边形的面积也相等。 ( )
错误解答: ( √ )
错误解答
课件PPT
正确解答:(?)
两个平行四边形的面积是否相等,应根据底和高的情况来判断。
易错提醒
正确解答
解:
学以致用
1.
找到平行四边形高所在的底。
计算下面平行四边形的面积。
S=ah
=12×10
=120(cm2)
课件PPT
?
解:
学以致用
2.
前提是底高相等的长方形和平行四边形。
判断:长方形的面积等于平行四边形的面积。 ( )
课件PPT
11.2÷5=2.24(cm)
解:
学以致用
3.
根据a=S÷h
已知一个平行四边形的一条高是5cm,面积是11.2cm2,求平行四边形这条高所对应的底边长。
底边长为2.24cm。
答:
课件PPT
课件PPT
4.判断:平行四边形只有一条高。 ( )
平行四边形有无数条高。
学以致用
解:
(?)
课件PPT
5.判断:平行四边形有一条边是10cm,有一条高是8cm,则该平行四边形面积一定是80cm2。 ( )
给出的边和高不一定是对应的底和高。
学以致用
解:
(?)
课堂小结
平行四边形面积怎样计算?
求平行四边形面积应注意什么?
1.长方形的长=平行四边形的底,长方形的宽=平行四边形的高。
3.应用公式计算平行四边形的面积时,底和高必须是对应的。
2.平行四边形的面积公式:S=ah、a=S÷h、h=S÷a。
谢谢
