五年级上册数学课件-5.2三角形的面积 西师大版(共26张PPT)
文档属性
| 名称 | 五年级上册数学课件-5.2三角形的面积 西师大版(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览




文档简介
第5单元 多边形面积的计算
2 三角形的面积
学习目标
1.掌握三角形的面积公式。
2.理解三角形的面积公式的推导过程。
平行四边形的面积公式:S=ah、a=S÷h、h=S÷a
复习导入
你还记得平行四边形的面积公式吗?
情景导入1
你能把三角形转化成我们会计算面积的图形并推导它的面积计算公式吗?
理解题意:
根据题意分别准备形状、大小完全一样的直角三角形、锐角三角形、钝角三角形纸片各两张。
探究新知
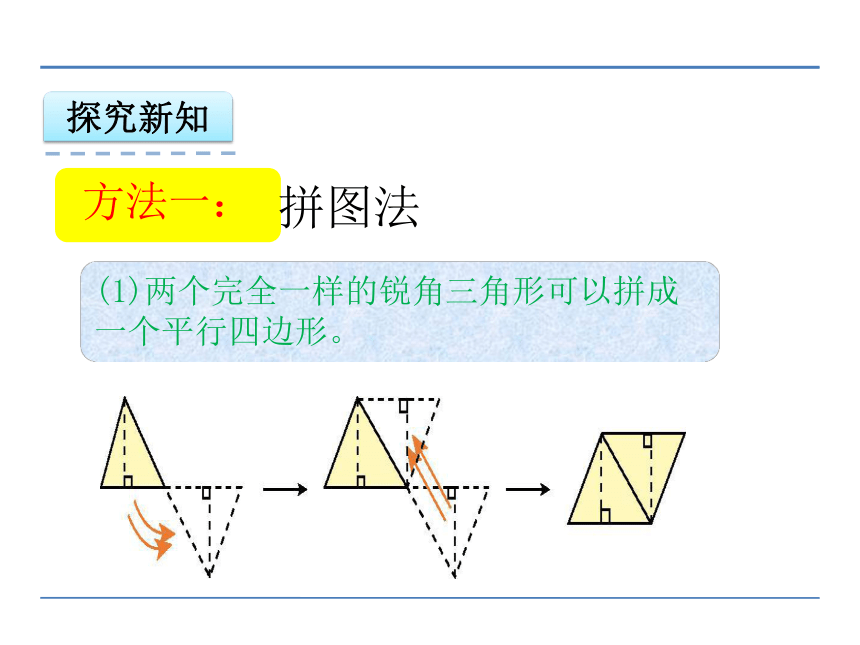
方法一:
(1)两个完全一样的锐角三角形可以拼成一个平行四边形。
拼图法
探究新知
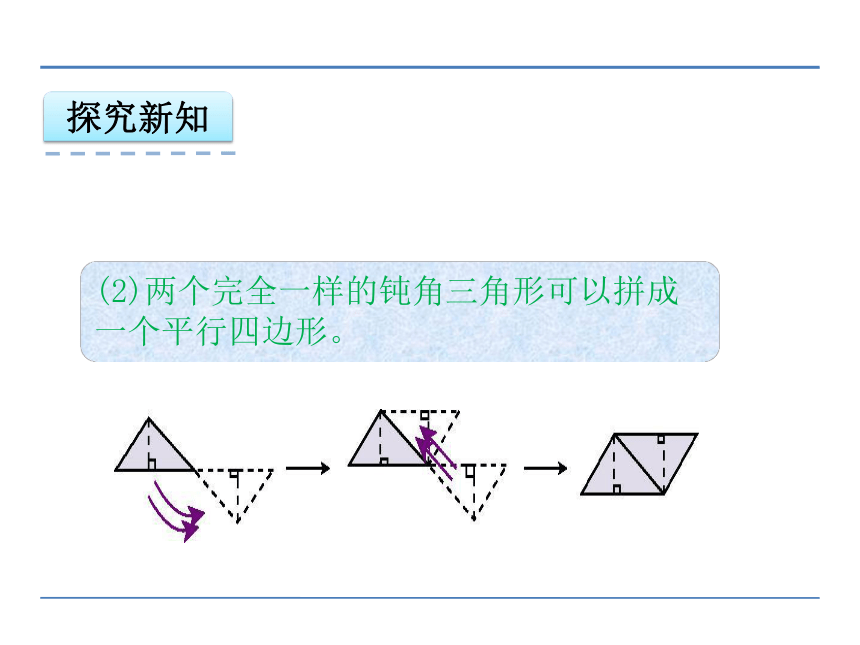
(2)两个完全一样的钝角三角形可以拼成一个平行四边形。
探究新知
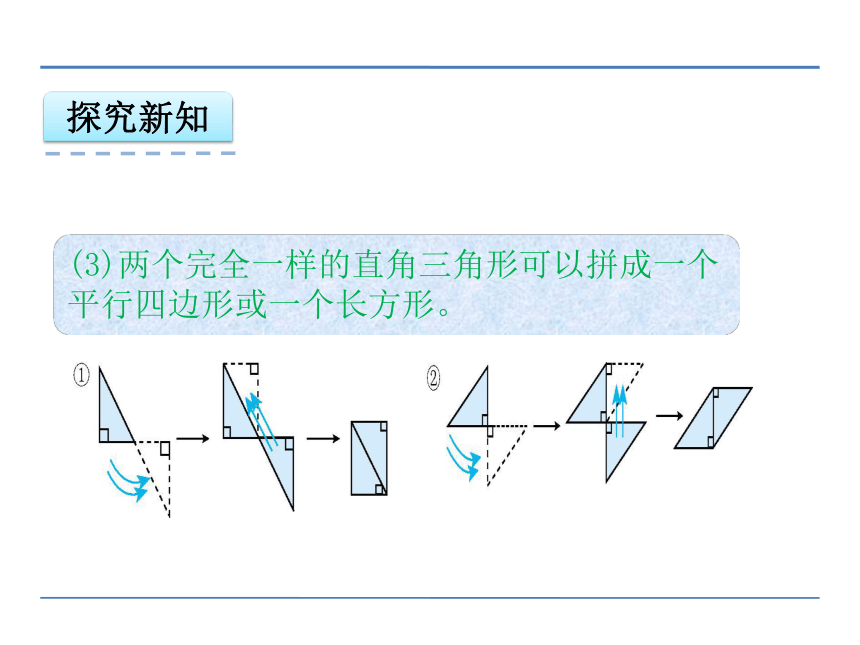
(3)两个完全一样的直角三角形可以拼成一个平行四边形或一个长方形。
探究新知
结论:
两个完全一样的三角形,可以拼成一个平行四边形或一个长方形。
平行四边形的底=三角形的底。平行四边形的高=三角形的高。两个三角形的面积=平行四边形的面积。
探究新知
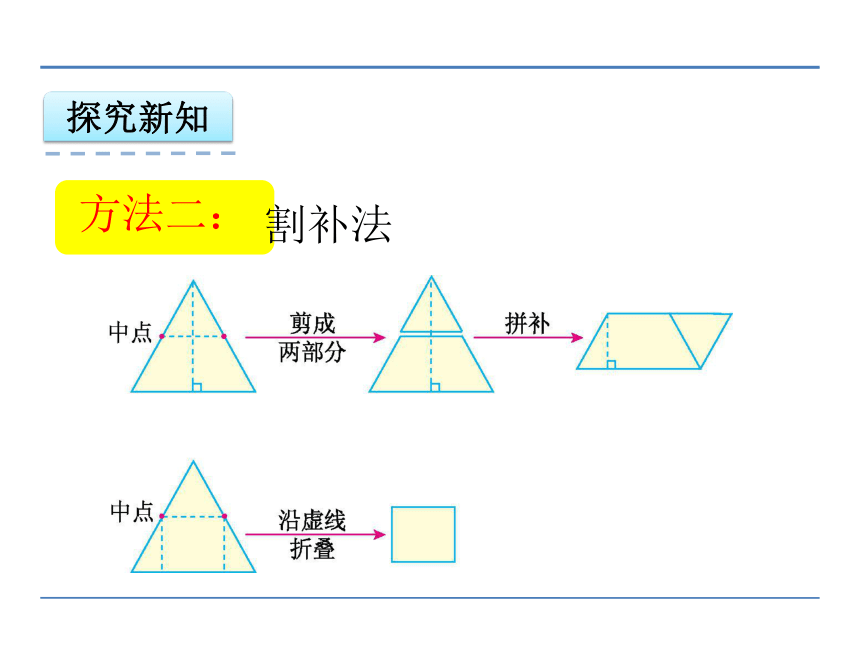
方法二:
割补法
探究新知
解决问题:
解:
平行四边形的面积=底×高 S=ah
三角形的面积=底×高 S=ah÷2
÷2
情景导入2
做小红旗。
(1)做200面这样的小红旗,至少需要多大面积的红纸?
(2)用一张长90cm、宽64cm的长方形红纸,可以做多少面这样的小红旗?
探究新知
问题(1):
已知两条直角边的长度,所以直接用三角形的面积公式就可以算出。所以200面小红旗的面积=200×一面小红旗的面积。
探究新知
解决问题:
解:
45×32÷2=720(cm2)
200×720=144000(cm2)
答:
至少需要144000cm2的红纸。
灵活运用三角形的面积公式, 即h=2S÷a、a=2S÷h。
探究新知
问题(2):
根据长方形的面积计算公式求出长方形红纸的面积,再用长方形红纸的面积除以一面小红旗的面积,就可以求出小红旗的面数。
探究新知
解决问题:
解:
90×64=5760(cm2)
5760÷720=8(面)
答:
可以做8面这样的小红旗。
典题精讲
解题思路:
1. 判断:平行四边形的面积是三角形面积的2倍。 ( )
三角形和平行四边形等底等高时,平行四边形的面积才是三角形面积的2倍。
解答:
( ?)
典题精讲
2.计算下面三角形的面积。
利用三角形面积公式计算。
S=ah÷2
=8×12÷2
=96÷2
=48(m2)
解答:
解答思路:
易错提醒
错误原因:没有强调两个完全相等的三角形。
判断:两个三角形一定能拼成一个平行四边形 ( )
错误解答: ( √ )
错误解答
课件PPT
正确解答:(?)
两个完全一样的三角形,可以拼成一个平行四边形或一个长方形。
易错提醒
正确解答
解:
学以致用
1.
利用三角形面积公式计算。
计算下面三角形的面积。
S=ah÷2
=4×1.5÷2
=6÷2
=3(cm2)
课件PPT
?
解:
学以致用
2.
等底等高的两个三角形面积一定相等,但面积相等的两个三角形不一定等底等高。
判断:面积相等的两个三角形,一定等底等高。 ( )
课件PPT
(75.5+124.5)×75.5÷2
=200×75.5÷2
=15100÷2
=7550(m2)
解:
学以致用
3.
根据S=ah÷2,但要先求出底。
一块三角形地的高是75.5m,比底少124.5m,这块地的面积是多少平方米?
这块地的面积是7550平方米。
答:
课件PPT
课件PPT
4.选择:一个三角形的面积是45平方米,高是12米,它的底是( )米。
A.7.5 B.3.75 C.15 D.1.875
根据a=2×S÷h
学以致用
解:
(A)
课件PPT
根据三角形面积公式计算。
学以致用
解:
S=ah÷2
=4.5×6.3÷2
=28.35÷2
≈14.2(m2)
5.计算下面三角形的面积。(结果保留一位小数)
课堂小结
三角形面积怎样计算?
求三角形面积应注意什么?
1.两个完全一样的三角形,可以拼成一个平行四边形或一个长方形。
3.灵活运用三角形的面积公式,解决实际生活中的有关三角形面积的问题,即h=2S÷a、a=2S÷h。
2.三角形的面积=底×高÷2。S=ah÷2。
谢谢
2 三角形的面积
学习目标
1.掌握三角形的面积公式。
2.理解三角形的面积公式的推导过程。
平行四边形的面积公式:S=ah、a=S÷h、h=S÷a
复习导入
你还记得平行四边形的面积公式吗?
情景导入1
你能把三角形转化成我们会计算面积的图形并推导它的面积计算公式吗?
理解题意:
根据题意分别准备形状、大小完全一样的直角三角形、锐角三角形、钝角三角形纸片各两张。
探究新知
方法一:
(1)两个完全一样的锐角三角形可以拼成一个平行四边形。
拼图法
探究新知
(2)两个完全一样的钝角三角形可以拼成一个平行四边形。
探究新知
(3)两个完全一样的直角三角形可以拼成一个平行四边形或一个长方形。
探究新知
结论:
两个完全一样的三角形,可以拼成一个平行四边形或一个长方形。
平行四边形的底=三角形的底。平行四边形的高=三角形的高。两个三角形的面积=平行四边形的面积。
探究新知
方法二:
割补法
探究新知
解决问题:
解:
平行四边形的面积=底×高 S=ah
三角形的面积=底×高 S=ah÷2
÷2
情景导入2
做小红旗。
(1)做200面这样的小红旗,至少需要多大面积的红纸?
(2)用一张长90cm、宽64cm的长方形红纸,可以做多少面这样的小红旗?
探究新知
问题(1):
已知两条直角边的长度,所以直接用三角形的面积公式就可以算出。所以200面小红旗的面积=200×一面小红旗的面积。
探究新知
解决问题:
解:
45×32÷2=720(cm2)
200×720=144000(cm2)
答:
至少需要144000cm2的红纸。
灵活运用三角形的面积公式, 即h=2S÷a、a=2S÷h。
探究新知
问题(2):
根据长方形的面积计算公式求出长方形红纸的面积,再用长方形红纸的面积除以一面小红旗的面积,就可以求出小红旗的面数。
探究新知
解决问题:
解:
90×64=5760(cm2)
5760÷720=8(面)
答:
可以做8面这样的小红旗。
典题精讲
解题思路:
1. 判断:平行四边形的面积是三角形面积的2倍。 ( )
三角形和平行四边形等底等高时,平行四边形的面积才是三角形面积的2倍。
解答:
( ?)
典题精讲
2.计算下面三角形的面积。
利用三角形面积公式计算。
S=ah÷2
=8×12÷2
=96÷2
=48(m2)
解答:
解答思路:
易错提醒
错误原因:没有强调两个完全相等的三角形。
判断:两个三角形一定能拼成一个平行四边形 ( )
错误解答: ( √ )
错误解答
课件PPT
正确解答:(?)
两个完全一样的三角形,可以拼成一个平行四边形或一个长方形。
易错提醒
正确解答
解:
学以致用
1.
利用三角形面积公式计算。
计算下面三角形的面积。
S=ah÷2
=4×1.5÷2
=6÷2
=3(cm2)
课件PPT
?
解:
学以致用
2.
等底等高的两个三角形面积一定相等,但面积相等的两个三角形不一定等底等高。
判断:面积相等的两个三角形,一定等底等高。 ( )
课件PPT
(75.5+124.5)×75.5÷2
=200×75.5÷2
=15100÷2
=7550(m2)
解:
学以致用
3.
根据S=ah÷2,但要先求出底。
一块三角形地的高是75.5m,比底少124.5m,这块地的面积是多少平方米?
这块地的面积是7550平方米。
答:
课件PPT
课件PPT
4.选择:一个三角形的面积是45平方米,高是12米,它的底是( )米。
A.7.5 B.3.75 C.15 D.1.875
根据a=2×S÷h
学以致用
解:
(A)
课件PPT
根据三角形面积公式计算。
学以致用
解:
S=ah÷2
=4.5×6.3÷2
=28.35÷2
≈14.2(m2)
5.计算下面三角形的面积。(结果保留一位小数)
课堂小结
三角形面积怎样计算?
求三角形面积应注意什么?
1.两个完全一样的三角形,可以拼成一个平行四边形或一个长方形。
3.灵活运用三角形的面积公式,解决实际生活中的有关三角形面积的问题,即h=2S÷a、a=2S÷h。
2.三角形的面积=底×高÷2。S=ah÷2。
谢谢
