六年级上册数学课件-3.8工程问题 人教版(共21张PPT)
文档属性
| 名称 | 六年级上册数学课件-3.8工程问题 人教版(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
《例7:工程问题》
人教版数学六年级
山东大学附属中学
学习准备
练习本、学历案、笔、数学课本。
(1)修一条360米的公路,甲队修12天完成,平均每天修(
)米。
30
工作总量÷工作时间=工作效率
(2)修一条360米的公路,甲队每天修18米,(
)天能完成。
20
工作总量÷工作效率=工作时间
(3)加工一批零件,计划8小时完成,平均每小时加工这批零件的(
)。
填一填
课前练习:
掌握用假设、验证等方法解决问题的基本策略,体会模型思想
如果两队合修,多少天能修完?
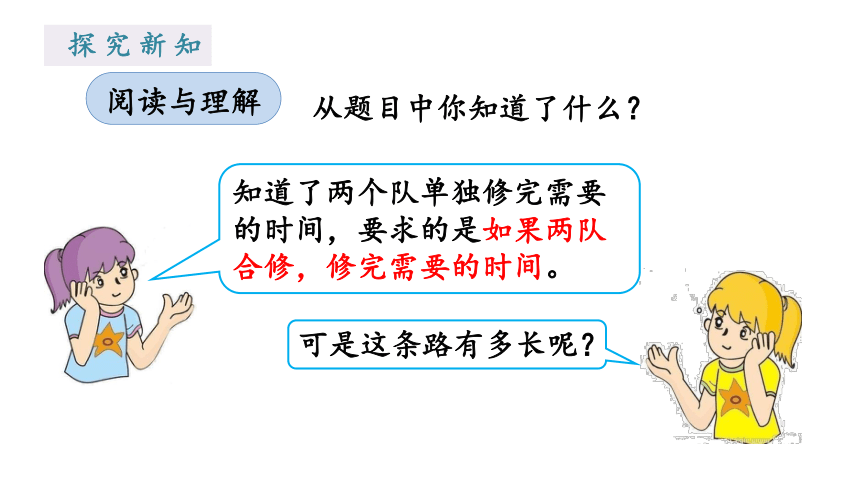
探究新知
阅读与理解
知道了两个队单独修完需要的时间,要求的是如果两队合修,修完需要的时间。
可是这条路有多长呢?
从题目中你知道了什么?
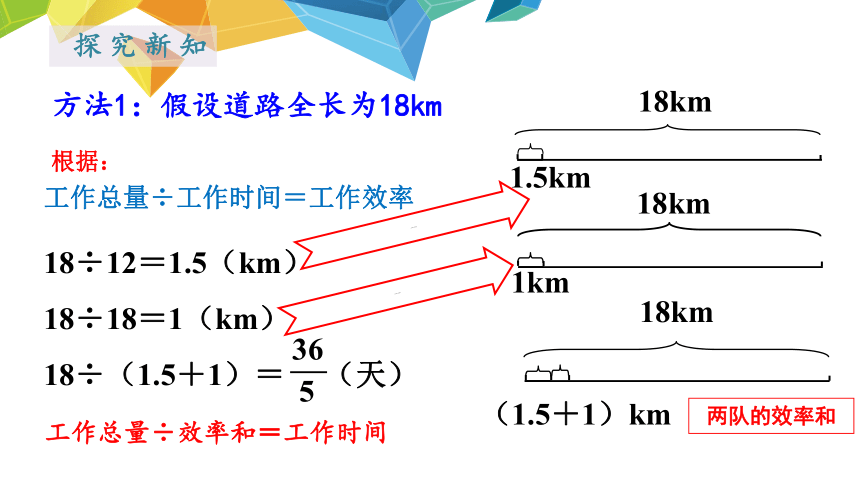
探究新知
方法1:假设道路全长为18km
18km
18km
18km
1.5km
1km
(1.5+1)km
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)=
(天)
5
36
工作总量÷工作时间=工作效率
根据:
一队的工作效率
二队的工作效率
两队的效率和
工作总量÷效率和=工作时间
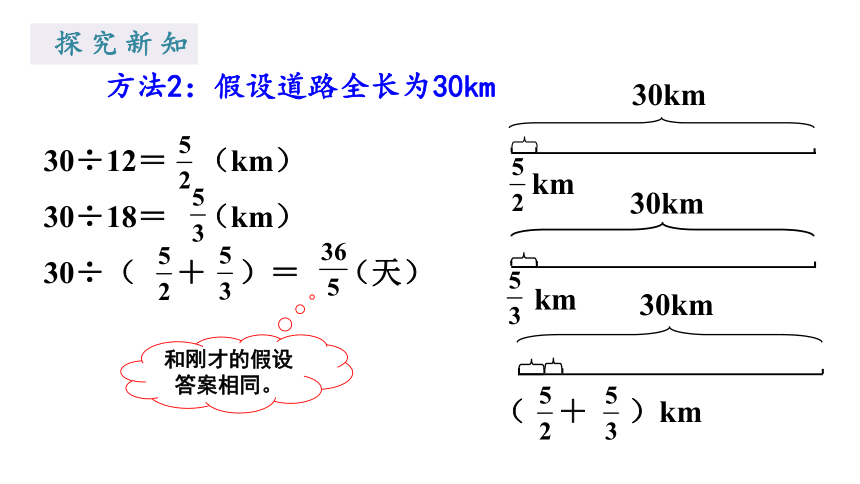
探究新知
方法2:假设道路全长为30km
30km
km
30km
km
30km
(
+
)km
30÷12=
(km)
30÷18=
(km)
30÷(
+
)=
(天)
和刚才的假设答案相同。
探究新知
问题:
①
我们假设这条路的长度都不同,但最终的结果是相同的,那么这条路的长度还可以看做是多少千米?
②
这条路的长度可以看做是“1”吗?
③
如果把这条路的长度看做是“1”,应该怎样解答?
小组讨论:
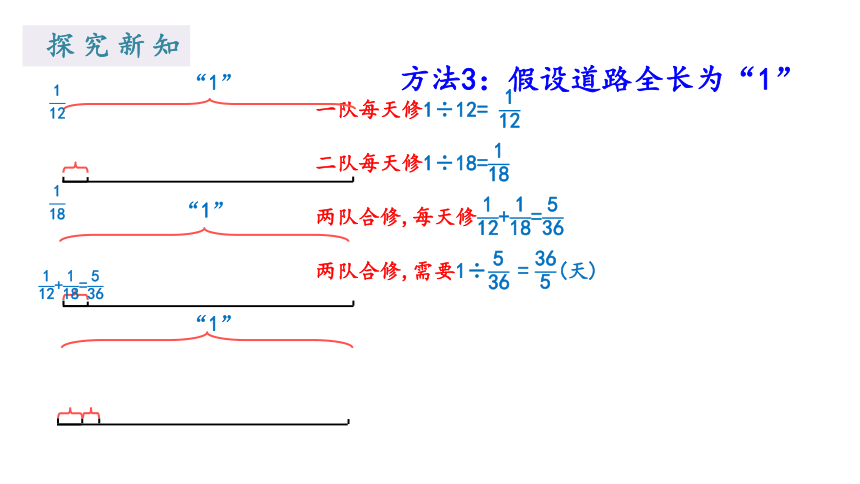
方法3:假设道路全长为“1”
一队每天修1÷12=
二队每天修1÷18=
两队合修,每天修+=
两队合修,需要1÷=
(天)
“1”
“1”
“1”
+=
探究新知
方法3:假设道路全长为“1”
“1”
“1”
“1”
+=
综合算式:
1÷(+)
=1÷
=(天)
答:两队合作天能修完。
探究新知
假设全长为18km
假设全长为30km
假设全长为“1”
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)=
(天)
5
36
30÷12=
(km)
30÷18=
(km)
30÷(
+
)=
(天)
探究新知
小结:
不管假设这条路有多长,答案都是相同的。把道路长假设成1,解答要简便。
探究新知
分别求出一队和二队天修的道路,再将它们加起来,看一看够不够单位“1”。
×
+
×
=0.6+0.4=1
把道路假设成不同的长度,得出了相同的结果,这个结果对吗?可以怎样检验?
探究新知
答:如果两队合修,天可以修完。
归纳总结:
解答工程问题要注意:
(1)把工作总量看作单位“1”.
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率。
(3)基本等量关系式:
工作总量÷工作效率之和=工作时间。
探究新知
一件工作,甲单独做需要4小时完成,乙单独做需要6小时完成,甲每小时完成这件工作的
,乙每小时完成这件工作的
,两人合做,每小时完成这件工作的
。
1.
填一填。
跟进练习
2.解决问题。
如果两辆车一起运,多少次能运完这批货物?
跟进练习
3.解决问题。
(1)一批货物,用小货车运需要12次运完,用大卡车运,只要4次运完。如果两车一起运,多少次运完这批货物?
跟进练习
(2)一辆小汽车从武汉到杭州需要8小时,一辆大客车从杭州到武汉需要10小时。两车同时从两地出发相向而行,几小时相遇?
跟进练习
这节课你有哪些收获?
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
利用抽象的“1”解决实际问题:
总结:
制作单位:山东大学附属中学
制作时间:
2020年9月
《例7:工程问题》
人教版数学六年级
山东大学附属中学
学习准备
练习本、学历案、笔、数学课本。
(1)修一条360米的公路,甲队修12天完成,平均每天修(
)米。
30
工作总量÷工作时间=工作效率
(2)修一条360米的公路,甲队每天修18米,(
)天能完成。
20
工作总量÷工作效率=工作时间
(3)加工一批零件,计划8小时完成,平均每小时加工这批零件的(
)。
填一填
课前练习:
掌握用假设、验证等方法解决问题的基本策略,体会模型思想
如果两队合修,多少天能修完?
探究新知
阅读与理解
知道了两个队单独修完需要的时间,要求的是如果两队合修,修完需要的时间。
可是这条路有多长呢?
从题目中你知道了什么?
探究新知
方法1:假设道路全长为18km
18km
18km
18km
1.5km
1km
(1.5+1)km
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)=
(天)
5
36
工作总量÷工作时间=工作效率
根据:
一队的工作效率
二队的工作效率
两队的效率和
工作总量÷效率和=工作时间
探究新知
方法2:假设道路全长为30km
30km
km
30km
km
30km
(
+
)km
30÷12=
(km)
30÷18=
(km)
30÷(
+
)=
(天)
和刚才的假设答案相同。
探究新知
问题:
①
我们假设这条路的长度都不同,但最终的结果是相同的,那么这条路的长度还可以看做是多少千米?
②
这条路的长度可以看做是“1”吗?
③
如果把这条路的长度看做是“1”,应该怎样解答?
小组讨论:
方法3:假设道路全长为“1”
一队每天修1÷12=
二队每天修1÷18=
两队合修,每天修+=
两队合修,需要1÷=
(天)
“1”
“1”
“1”
+=
探究新知
方法3:假设道路全长为“1”
“1”
“1”
“1”
+=
综合算式:
1÷(+)
=1÷
=(天)
答:两队合作天能修完。
探究新知
假设全长为18km
假设全长为30km
假设全长为“1”
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)=
(天)
5
36
30÷12=
(km)
30÷18=
(km)
30÷(
+
)=
(天)
探究新知
小结:
不管假设这条路有多长,答案都是相同的。把道路长假设成1,解答要简便。
探究新知
分别求出一队和二队天修的道路,再将它们加起来,看一看够不够单位“1”。
×
+
×
=0.6+0.4=1
把道路假设成不同的长度,得出了相同的结果,这个结果对吗?可以怎样检验?
探究新知
答:如果两队合修,天可以修完。
归纳总结:
解答工程问题要注意:
(1)把工作总量看作单位“1”.
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率。
(3)基本等量关系式:
工作总量÷工作效率之和=工作时间。
探究新知
一件工作,甲单独做需要4小时完成,乙单独做需要6小时完成,甲每小时完成这件工作的
,乙每小时完成这件工作的
,两人合做,每小时完成这件工作的
。
1.
填一填。
跟进练习
2.解决问题。
如果两辆车一起运,多少次能运完这批货物?
跟进练习
3.解决问题。
(1)一批货物,用小货车运需要12次运完,用大卡车运,只要4次运完。如果两车一起运,多少次运完这批货物?
跟进练习
(2)一辆小汽车从武汉到杭州需要8小时,一辆大客车从杭州到武汉需要10小时。两车同时从两地出发相向而行,几小时相遇?
跟进练习
这节课你有哪些收获?
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
利用抽象的“1”解决实际问题:
总结:
制作单位:山东大学附属中学
制作时间:
2020年9月
