初中数学鲁教版七年级上册第六章5一次函数的应用练习题-普通用卷(word版含答案)
文档属性
| 名称 | 初中数学鲁教版七年级上册第六章5一次函数的应用练习题-普通用卷(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 10:07:57 | ||
图片预览



文档简介
初中数学鲁教版七年级上册第六章5一次函数的应用练习题
一、选择
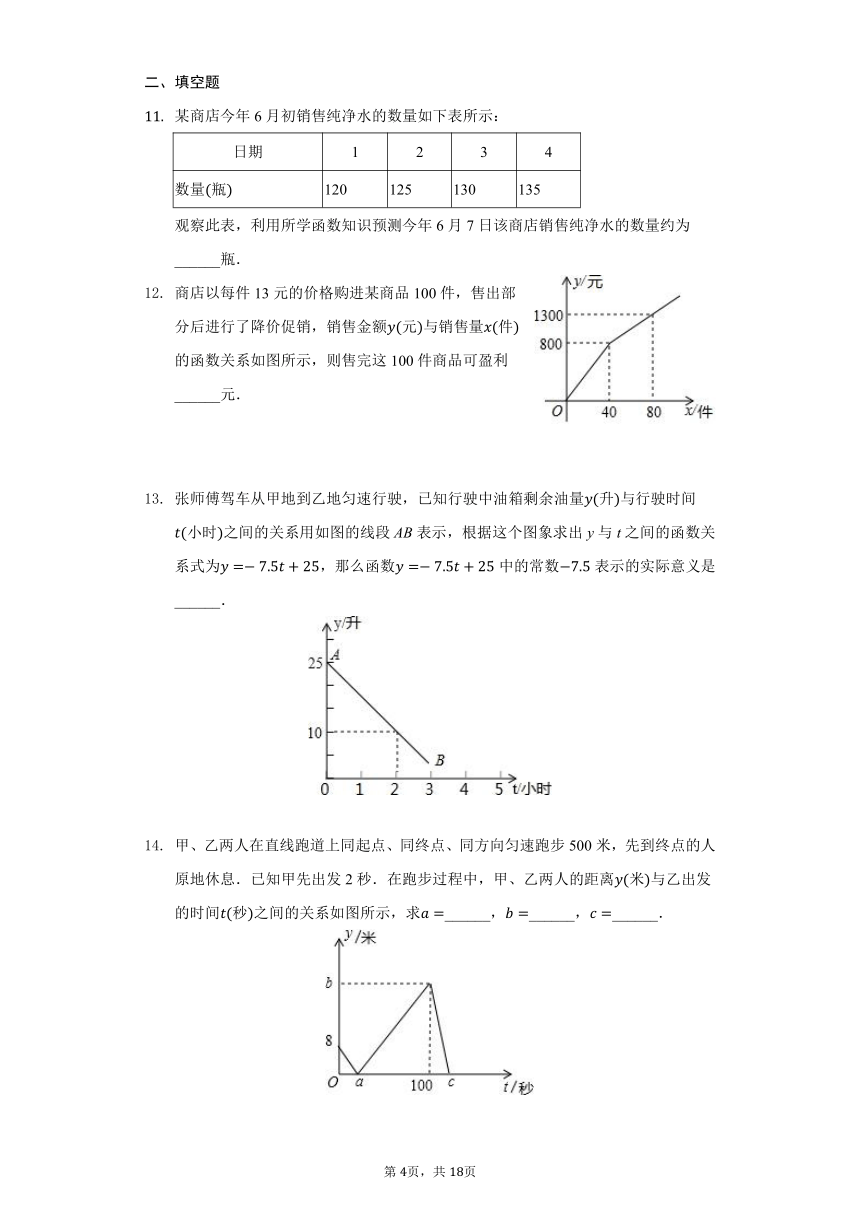
A、B两地相距20千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程千米与时间小时之间的关系.下列说法错误的是
A.
乙晚出发1小时
B.
乙出发3小时后追上甲
C.
甲的速度是4千米小时
D.
乙先到达B地
甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离与运动时间的函数关系大致如图所示,下列说法中错误的是
A.
两人出发1小时后相遇
B.
赵明阳跑步的速度为
C.
王浩月到达目的地时两人相距10km
D.
王浩月比赵明阳提前到目的地
数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点P,根据图象可知,方程的解是
A.
B.
C.
D.
如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长单位:关于所挂物体质量单位:的函数图象如图所示,则图中a的值是
A.
3
B.
4
C.
5
D.
6
如图是本地区一种产品30天的销售图象,图是产品日销售量单位:件与时间单位;天的函数关系,图是一件产品的销售利润单位:元与时间单位:天的函数关系,已知日销售利润日销售量一件产品的销售利润,下列结论错误的是
A.
第24天的销售量为200件
B.
第10天销售一件产品的利润是15元
C.
第12天与第30天这两天的日销售利润相等
D.
第27天的日销售利润是875元
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,乙从B地到A地需要分钟.
A.
12
B.
14
C.
18
D.
20
某生物小组观察一植物生长,得到的植物高度单位:厘米与观察时间单位:天的关系,并画出如图所示的图象是线段,直线CD平行于x轴下列说法正确的是
从开始观察时起,50天后该植物停止长高;
直线AC的函数表达式为;
第40天,该植物的高度为14厘米;
该植物最高为15厘米.
A.
B.
C.
D.
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度为
A.
10米秒
B.
11米秒
C.
12米秒
D.
13米秒
小兰和小琳约好在公共汽车站一起乘车去博物馆,小兰从家出发步行到车站,等小琳到了以后两人一起乘公共汽车到博物馆.图中的折线表示小兰距离博物馆的路程与所用时间之间的函数关系,下列说法错误的是
A.
小兰从家到公共汽车站步行了1km
B.
小兰在公共汽车站等汽车用了15min
C.
公共汽车的平均速度为
D.
小兰和小琳乘公共汽车用了55min
甲、乙两人从同一地点出发,沿同一方向跑步,速度分别为4米秒和6米秒,开始时甲先跑100米后乙再追赶,则从乙出发开始追上甲这一过程中,甲、乙两人之间的距离米与乙跑步所用时间秒之间的函数表达式为
A.
B.
C.
D.
二、填空题
某商店今年6月初销售纯净水的数量如下表所示:
日期
1
2
3
4
数量瓶
120
125
130
135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为______瓶.
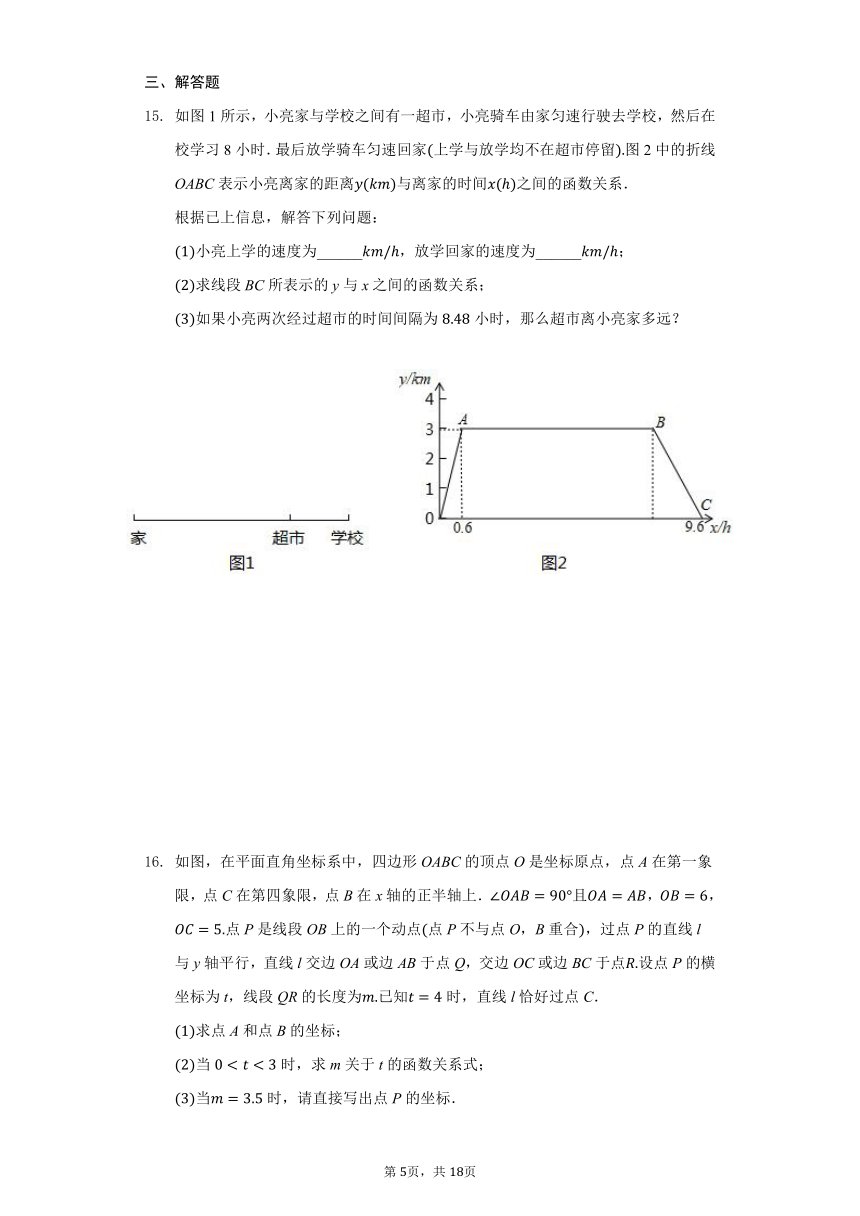
商店以每件13元的价格购进某商品100件,售出部分后进行了降价促销,销售金额元与销售量件的函数关系如图所示,则售完这100件商品可盈利______元.
张师傅驾车从甲地到乙地匀速行驶,已知行驶中油箱剩余油量升与行驶时间小时之间的关系用如图的线段AB表示,根据这个图象求出y与t之间的函数关系式为,那么函数中的常数表示的实际意义是______.
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离米与乙出发的时间秒之间的关系如图所示,求______,______,______.
三、解答题
如图1所示,小亮家与学校之间有一超市,小亮骑车由家匀速行驶去学校,然后在校学习8小时.最后放学骑车匀速回家上学与放学均不在超市停留图2中的折线OABC表示小亮离家的距离与离家的时间之间的函数关系.
根据已上信息,解答下列问题:
小亮上学的速度为______,放学回家的速度为______;
求线段BC所表示的y与x之间的函数关系;
如果小亮两次经过超市的时间间隔为小时,那么超市离小亮家多远?
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.且,,点P是线段OB上的一个动点点P不与点O,B重合,过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点设点P的横坐标为t,线段QR的长度为已知时,直线l恰好过点C.
求点A和点B的坐标;
当时,求m关于t的函数关系式;
当时,请直接写出点P的坐标.
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过210度时,按元度计费;月用电量超过210度时,其中的210度仍按元度计费,超过部分按元度计费.设每户家庭月用电量为x度时,应交电费y元.
分别求出当和时,y与x之间的关系式;
小明家5月份交电费元,则小明家这个月用电多少度?
某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林上下车时间忽略不计第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程米与时间分的函数关系如图2所示.
求第一班车离入口处的路程米与时间分的函数表达式.
求第一班车从入口处到达塔林所需的时间.
小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?假设每一班车速度均相同,小聪步行速度不变
答案和解析
1.【答案】B
【解析】解:由图象可得,
乙晚出发1小时,故选项A正确;
乙出发小时追上甲,故选项B错误;
甲的速度是千米小时,故选项C正确;
乙先到达B地,故选项D正确;
故选:B.
根据函数图象中的数据,可以判断各个选项中的说法是否正确,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
2.【答案】C
【解析】解:由图象可知,
两人出发1小时后相遇,故选项A正确;
赵明阳跑步的速度为,故选项B正确;
王皓月的速度为:,
王皓月从开始到到达目的地用的时间为:,
故王浩月到达目的地时两人相距,故选项C错误;
王浩月比赵明阳提前到目的地,故选项D正确;
故选:C.
根据函数图象中的数据,可以分别计算出两人的速度,从而可以判断各个选项中的说法是否正确,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
3.【答案】A
【解析】解:直线和直线相交于点
直线和直线相交于点P为.
故选:A.
根据函数图象交点的横坐标是关于x的方程的解,可得答案.
本题考查了一次函数与一元一次方程,两个一次函数图象的交点的横坐标是相应方程的解.
4.【答案】A
【解析】解:设y与x的函数关系式为,
,
解得,,
即y与x的函数关系式是,
当时,,得,
即a的值为3,
故选:A.
根据题目中的函数解析式,可以求得y与x的函数关系式,然后令,求出x的值,即此时x的值就是a的值,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
5.【答案】C
【解析】解:A、根据图可得第24天的销售量为200件,故正确;
B、设当,一件产品的销售利润单位:元与时间单位:天的函数关系为,
把,代入得:
解得:,
,
当时,,
故正确;
C、当时,设产品日销售量单位:件与时间单位;天的函数关系为,
把,代入得:,
解得:,
,
当时,,,
第12天的日销售利润为;元,第30天的日销售利润为;元,
,故C错误;
D、第27天的日销售利润为元,故正确.
故选:C.
根据函数图象分别求出设当,一件产品的销售利润单位:元与时间单位:天的函数关系为,当时,设产品日销售量单位:件与时间单位;天的函数关系为,根据日销售利润日销售量一件产品的销售利润,即可进行判断.
本题考查了一次函数的应用,解决本题的关键是利用待定系数法求函数解析式.
6.【答案】A
【解析】解:由图象可得,
从A地到B地的路程是16km,
甲的速度为千米分钟,
乙的速度为:千米分钟,
故乙从B地到A地需要:分钟,
故选:A.
根据函数图象中的数据,可以分别计算出甲、乙两人的速度,然后由图象可知,从A地到B地的路程是16km,从而可以计算出乙从B地到A地需要几分钟,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
7.【答案】A
【解析】
【分析】
本题考查了一次函数的应用,主要利用了一次函数解析式的求法,已知自变量求函数值,仔细观察图象,准确获取信息是解题的关键.
根据平行线间的距离相等可知50天后植物的高度不变,也就是停止长高;
设直线AC的解析式为,然后求出直线AC线段的解析式,
把代入的结论进行计算即可得解;
把代入的结论进行计算即可得解.
【解答】
解:轴,
从第50天开始植物的高度不变,
故的说法正确;
设直线AC的解析式为,
经过点,,
,,
解得,,
所以,直线AC的解析式为,
故的结论正确;
当时,,
即第40天,该植物的高度为14厘米;
故的说法正确;
当时,,
即第50天,该植物的高度为16厘米;
故的说法错误.
综上所述,正确的是.
故选:A.
8.【答案】B
【解析】解:设甲车的速度为,乙车的速度为,
由图象可知:
开始时,乙车与甲车相距300米,
乙车用100秒追上了甲车,
,
装完货物后,甲乙两车行驶了20秒后,两车相距500米,
,
,
解得:,
故选:B.
设甲车的速度为,乙车的速度为,根据图象给出的等量关系即可求出答案.
本题考查一次函数,解题的关键是找出图象中所隐含的等量关系,本题属于中等题型.
9.【答案】D
【解析】解:A、小兰从家到公共汽车站步行了1km,正确;
B、小兰在公共汽车站等汽车用了15min,正确;
C、公共汽车的平均速度为,正确;
D、小兰和小琳乘公共汽车用了,错误;
故选:D.
根据图象可以确定小兰离公共汽车站1公里,步行用了多长时间,等公交车时间是多少,两人乘公交车运行的时间和对应的路程,然后确定各自的速度.
本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
10.【答案】B
【解析】
【分析】
本题考查了根据实际问题抽象一次函数关系式的知识,解答本题的关键是得出两人距离的表达式甲t秒运动的距离为4t米,乙t秒运动的距离为6t米,则,合并后即可得出s与t的关系式.
【解答】
解:由题意得,甲t秒运动的距离为4t米,乙t秒运动的距离为6t米,
则,
当时,,
故可得.
故选B.
11.【答案】150
【解析】解:这是一个一次函数模型,设,则有,
解得,
,
当时,,
预测今年6月7日该商店销售纯净水的数量约为150瓶,
故答案为150.
这是一个一次函数模型,设,利用待定系数法即可解决问题,
本题考查一次函数的性质,解题的关键是学会构建一次函数解决问题,属于中考常考题型.
12.【答案】250
【解析】解:设降价段图象的表达式为:,
将、代入上式并解得:,
即每件售价元;
从图象看,售出80件即收回成本,
利润即为剩下的20件的售出金额,即为:,
故答案为:250.
设降价段图象的表达式为:,将、代入上式并解得:,即每件售价元;从图象看,售出80件即收回成本,利润即为剩下的20件的售出金额,即可求解.
此题为一次函数的应用,渗透了函数与方程的思想,重点是求降价后每件的价格.
13.【答案】表示每小时耗油升
【解析】解:函数中的常数表示的实际意义是表示每小时耗油升.
故答案为表示每小时耗油升
又经过2小时,汽车油箱剩余油量10升,即每小时耗油升.
本题考查了一次函数的应用,读懂题意,观察图象提供的信息,利用数形结合是解题的关键.
14.【答案】8秒?
92米?
123秒
【解析】解:由图象,得
甲的速度为:米秒,
乙的速度为:米秒,
乙走完全程时甲乙相距的路程为:米,
乙追上甲的时间为:秒,
乙出发后甲走完全程所用的时间为:秒.
故答案为:8秒,92米,123秒.
由图象可以看出甲2秒跑了8米可以求出甲的速度为4米秒,b是表示乙跑到终点时甲乙的距离,由乙跑的距离甲跑的距离就可以得出结论,c表示乙出发后甲到达终点的时间.根据总路程速度甲先走的时间即是c的值.
本题是一道一次函数的综合试题,考查了路程速度时间的运用,追击问题的运用,解答时求出甲、乙的速度是解答本题的关键.
15.【答案】,3;
设线段BC所表示的y与x之间的函数关系式为,
将、代入,得
,得,
线段BC所表示的y与x之间的函数关系式为;
设超市离家skm,
,
解得:.
答:超市离家.
【解析】
解:由题意可得,
小明上学的速度为:,
放学回家的速度为:,
故答案为:5,3;
见答案;
见答案.
【分析】
根据题意和图象中的数据可以求得小亮上学的速度和放学回家的速度;
根据图象中的数据和题意可以求得线段BC所表示的y与x之间的函数关系;
由题意可知,小明从家到超市和从超市到家的时间之和是总的时间减去两次经过超市的时间间隔,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
16.【答案】解:如图:过点A作于M,
,,,,
,
点A的坐标为,点B的坐标为;
作轴于N,如图,
时,直线l恰好过点C,
,
在中,,
点坐标为,
设直线OC的解析式为,
把代入得,解得,
直线OC的解析式为,
设直线OA的解析式为,
把代入得,解得,
直线OA的解析式为,
,
,,
,
即;
设直线AB的解析式为,
把,代入得:,解得,
直线AB的解析式为,
同理可得直线BC的解析式为,
当时,,
若,则,
解得,
此时P点坐标为;
当时,,,
,
若,则,
解得不合题意舍去;
当时,,,
,
若,则,
解得,此时P点坐标为;
综上所述,满足条件的P点坐标为或.
【解析】根据等腰直角三角形的性质即可解决问题;
作轴于N,如图,先利用勾股定理计算出CN得到C点坐标为,再利用待定系数法分别求出直线OC的解析式,直线OA的解析式,则根据一次函数图象上点的坐标特征得到Q、R的坐标,从而得到m关于t的函数关系式;
利用待定系数法求出直线AB的解析式,直线BC的解析式,然后分类讨论:当,,当时,分别列出方程,然后解方程求出t得到P点坐标.
本题是一次函数综合题,考查了等腰直角三角形的性质和一次函数图象上点的坐标特征;会运用待定系数法求一次函数解析式;理解坐标与图形性质,会利用点的坐标表示线段的长;学会运用分类讨论的思想解决数学问题.
17.【答案】解:当时,y与x的函数解析式是;
当时,y与x的函数解析式:,
即;
因为小明家5月份的电费超过元,
所以把代入中,得.
答:小明家5月份用电210度.
【解析】时,电费y就是乘以相应度数;时,电费超过210的度数;
把代入得到的函数解析式中,求解即可.
本题考查一次函数的应用;得到超过210度的电费的计算方式是解决本题的易错点.
18.【答案】解:由题意得,可设函数表达式为:,
把,代入,得,解得,
第一班车离入口处的路程米与时间分的函数表达为;
把代入,解得,
分,
第一班车从入口处到达塔林所需时间10分钟;
设小聪坐上了第n班车,则
,解得,
小聪坐上了第5班车,
等车的时间为5分钟,坐班车所需时间为:分,
步行所需时间:分,
分,
比他在塔林游玩结束后立即步行到草甸提早了7分钟.
【解析】设,运用待定系数法求解即可;
把代入的结论即可;
设小聪坐上了第n班车,,解得,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可.
本题主要考查了一次函数的应用,熟练掌握待定系数法求出函数解析式是解答本题的关键.
第2页,共18页
第1页,共18页
一、选择
A、B两地相距20千米,甲、乙两人都从A地去B地,图中和分别表示甲、乙两人所走路程千米与时间小时之间的关系.下列说法错误的是
A.
乙晚出发1小时
B.
乙出发3小时后追上甲
C.
甲的速度是4千米小时
D.
乙先到达B地
甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离与运动时间的函数关系大致如图所示,下列说法中错误的是
A.
两人出发1小时后相遇
B.
赵明阳跑步的速度为
C.
王浩月到达目的地时两人相距10km
D.
王浩月比赵明阳提前到目的地
数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点P,根据图象可知,方程的解是
A.
B.
C.
D.
如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长单位:关于所挂物体质量单位:的函数图象如图所示,则图中a的值是
A.
3
B.
4
C.
5
D.
6
如图是本地区一种产品30天的销售图象,图是产品日销售量单位:件与时间单位;天的函数关系,图是一件产品的销售利润单位:元与时间单位:天的函数关系,已知日销售利润日销售量一件产品的销售利润,下列结论错误的是
A.
第24天的销售量为200件
B.
第10天销售一件产品的利润是15元
C.
第12天与第30天这两天的日销售利润相等
D.
第27天的日销售利润是875元
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,乙从B地到A地需要分钟.
A.
12
B.
14
C.
18
D.
20
某生物小组观察一植物生长,得到的植物高度单位:厘米与观察时间单位:天的关系,并画出如图所示的图象是线段,直线CD平行于x轴下列说法正确的是
从开始观察时起,50天后该植物停止长高;
直线AC的函数表达式为;
第40天,该植物的高度为14厘米;
该植物最高为15厘米.
A.
B.
C.
D.
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y米,y关于x的函数关系如图所示,则甲车的速度为
A.
10米秒
B.
11米秒
C.
12米秒
D.
13米秒
小兰和小琳约好在公共汽车站一起乘车去博物馆,小兰从家出发步行到车站,等小琳到了以后两人一起乘公共汽车到博物馆.图中的折线表示小兰距离博物馆的路程与所用时间之间的函数关系,下列说法错误的是
A.
小兰从家到公共汽车站步行了1km
B.
小兰在公共汽车站等汽车用了15min
C.
公共汽车的平均速度为
D.
小兰和小琳乘公共汽车用了55min
甲、乙两人从同一地点出发,沿同一方向跑步,速度分别为4米秒和6米秒,开始时甲先跑100米后乙再追赶,则从乙出发开始追上甲这一过程中,甲、乙两人之间的距离米与乙跑步所用时间秒之间的函数表达式为
A.
B.
C.
D.
二、填空题
某商店今年6月初销售纯净水的数量如下表所示:
日期
1
2
3
4
数量瓶
120
125
130
135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为______瓶.
商店以每件13元的价格购进某商品100件,售出部分后进行了降价促销,销售金额元与销售量件的函数关系如图所示,则售完这100件商品可盈利______元.
张师傅驾车从甲地到乙地匀速行驶,已知行驶中油箱剩余油量升与行驶时间小时之间的关系用如图的线段AB表示,根据这个图象求出y与t之间的函数关系式为,那么函数中的常数表示的实际意义是______.
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离米与乙出发的时间秒之间的关系如图所示,求______,______,______.
三、解答题
如图1所示,小亮家与学校之间有一超市,小亮骑车由家匀速行驶去学校,然后在校学习8小时.最后放学骑车匀速回家上学与放学均不在超市停留图2中的折线OABC表示小亮离家的距离与离家的时间之间的函数关系.
根据已上信息,解答下列问题:
小亮上学的速度为______,放学回家的速度为______;
求线段BC所表示的y与x之间的函数关系;
如果小亮两次经过超市的时间间隔为小时,那么超市离小亮家多远?
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.且,,点P是线段OB上的一个动点点P不与点O,B重合,过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点设点P的横坐标为t,线段QR的长度为已知时,直线l恰好过点C.
求点A和点B的坐标;
当时,求m关于t的函数关系式;
当时,请直接写出点P的坐标.
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过210度时,按元度计费;月用电量超过210度时,其中的210度仍按元度计费,超过部分按元度计费.设每户家庭月用电量为x度时,应交电费y元.
分别求出当和时,y与x之间的关系式;
小明家5月份交电费元,则小明家这个月用电多少度?
某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林上下车时间忽略不计第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程米与时间分的函数关系如图2所示.
求第一班车离入口处的路程米与时间分的函数表达式.
求第一班车从入口处到达塔林所需的时间.
小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?假设每一班车速度均相同,小聪步行速度不变
答案和解析
1.【答案】B
【解析】解:由图象可得,
乙晚出发1小时,故选项A正确;
乙出发小时追上甲,故选项B错误;
甲的速度是千米小时,故选项C正确;
乙先到达B地,故选项D正确;
故选:B.
根据函数图象中的数据,可以判断各个选项中的说法是否正确,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
2.【答案】C
【解析】解:由图象可知,
两人出发1小时后相遇,故选项A正确;
赵明阳跑步的速度为,故选项B正确;
王皓月的速度为:,
王皓月从开始到到达目的地用的时间为:,
故王浩月到达目的地时两人相距,故选项C错误;
王浩月比赵明阳提前到目的地,故选项D正确;
故选:C.
根据函数图象中的数据,可以分别计算出两人的速度,从而可以判断各个选项中的说法是否正确,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
3.【答案】A
【解析】解:直线和直线相交于点
直线和直线相交于点P为.
故选:A.
根据函数图象交点的横坐标是关于x的方程的解,可得答案.
本题考查了一次函数与一元一次方程,两个一次函数图象的交点的横坐标是相应方程的解.
4.【答案】A
【解析】解:设y与x的函数关系式为,
,
解得,,
即y与x的函数关系式是,
当时,,得,
即a的值为3,
故选:A.
根据题目中的函数解析式,可以求得y与x的函数关系式,然后令,求出x的值,即此时x的值就是a的值,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
5.【答案】C
【解析】解:A、根据图可得第24天的销售量为200件,故正确;
B、设当,一件产品的销售利润单位:元与时间单位:天的函数关系为,
把,代入得:
解得:,
,
当时,,
故正确;
C、当时,设产品日销售量单位:件与时间单位;天的函数关系为,
把,代入得:,
解得:,
,
当时,,,
第12天的日销售利润为;元,第30天的日销售利润为;元,
,故C错误;
D、第27天的日销售利润为元,故正确.
故选:C.
根据函数图象分别求出设当,一件产品的销售利润单位:元与时间单位:天的函数关系为,当时,设产品日销售量单位:件与时间单位;天的函数关系为,根据日销售利润日销售量一件产品的销售利润,即可进行判断.
本题考查了一次函数的应用,解决本题的关键是利用待定系数法求函数解析式.
6.【答案】A
【解析】解:由图象可得,
从A地到B地的路程是16km,
甲的速度为千米分钟,
乙的速度为:千米分钟,
故乙从B地到A地需要:分钟,
故选:A.
根据函数图象中的数据,可以分别计算出甲、乙两人的速度,然后由图象可知,从A地到B地的路程是16km,从而可以计算出乙从B地到A地需要几分钟,本题得以解决.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
7.【答案】A
【解析】
【分析】
本题考查了一次函数的应用,主要利用了一次函数解析式的求法,已知自变量求函数值,仔细观察图象,准确获取信息是解题的关键.
根据平行线间的距离相等可知50天后植物的高度不变,也就是停止长高;
设直线AC的解析式为,然后求出直线AC线段的解析式,
把代入的结论进行计算即可得解;
把代入的结论进行计算即可得解.
【解答】
解:轴,
从第50天开始植物的高度不变,
故的说法正确;
设直线AC的解析式为,
经过点,,
,,
解得,,
所以,直线AC的解析式为,
故的结论正确;
当时,,
即第40天,该植物的高度为14厘米;
故的说法正确;
当时,,
即第50天,该植物的高度为16厘米;
故的说法错误.
综上所述,正确的是.
故选:A.
8.【答案】B
【解析】解:设甲车的速度为,乙车的速度为,
由图象可知:
开始时,乙车与甲车相距300米,
乙车用100秒追上了甲车,
,
装完货物后,甲乙两车行驶了20秒后,两车相距500米,
,
,
解得:,
故选:B.
设甲车的速度为,乙车的速度为,根据图象给出的等量关系即可求出答案.
本题考查一次函数,解题的关键是找出图象中所隐含的等量关系,本题属于中等题型.
9.【答案】D
【解析】解:A、小兰从家到公共汽车站步行了1km,正确;
B、小兰在公共汽车站等汽车用了15min,正确;
C、公共汽车的平均速度为,正确;
D、小兰和小琳乘公共汽车用了,错误;
故选:D.
根据图象可以确定小兰离公共汽车站1公里,步行用了多长时间,等公交车时间是多少,两人乘公交车运行的时间和对应的路程,然后确定各自的速度.
本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
10.【答案】B
【解析】
【分析】
本题考查了根据实际问题抽象一次函数关系式的知识,解答本题的关键是得出两人距离的表达式甲t秒运动的距离为4t米,乙t秒运动的距离为6t米,则,合并后即可得出s与t的关系式.
【解答】
解:由题意得,甲t秒运动的距离为4t米,乙t秒运动的距离为6t米,
则,
当时,,
故可得.
故选B.
11.【答案】150
【解析】解:这是一个一次函数模型,设,则有,
解得,
,
当时,,
预测今年6月7日该商店销售纯净水的数量约为150瓶,
故答案为150.
这是一个一次函数模型,设,利用待定系数法即可解决问题,
本题考查一次函数的性质,解题的关键是学会构建一次函数解决问题,属于中考常考题型.
12.【答案】250
【解析】解:设降价段图象的表达式为:,
将、代入上式并解得:,
即每件售价元;
从图象看,售出80件即收回成本,
利润即为剩下的20件的售出金额,即为:,
故答案为:250.
设降价段图象的表达式为:,将、代入上式并解得:,即每件售价元;从图象看,售出80件即收回成本,利润即为剩下的20件的售出金额,即可求解.
此题为一次函数的应用,渗透了函数与方程的思想,重点是求降价后每件的价格.
13.【答案】表示每小时耗油升
【解析】解:函数中的常数表示的实际意义是表示每小时耗油升.
故答案为表示每小时耗油升
又经过2小时,汽车油箱剩余油量10升,即每小时耗油升.
本题考查了一次函数的应用,读懂题意,观察图象提供的信息,利用数形结合是解题的关键.
14.【答案】8秒?
92米?
123秒
【解析】解:由图象,得
甲的速度为:米秒,
乙的速度为:米秒,
乙走完全程时甲乙相距的路程为:米,
乙追上甲的时间为:秒,
乙出发后甲走完全程所用的时间为:秒.
故答案为:8秒,92米,123秒.
由图象可以看出甲2秒跑了8米可以求出甲的速度为4米秒,b是表示乙跑到终点时甲乙的距离,由乙跑的距离甲跑的距离就可以得出结论,c表示乙出发后甲到达终点的时间.根据总路程速度甲先走的时间即是c的值.
本题是一道一次函数的综合试题,考查了路程速度时间的运用,追击问题的运用,解答时求出甲、乙的速度是解答本题的关键.
15.【答案】,3;
设线段BC所表示的y与x之间的函数关系式为,
将、代入,得
,得,
线段BC所表示的y与x之间的函数关系式为;
设超市离家skm,
,
解得:.
答:超市离家.
【解析】
解:由题意可得,
小明上学的速度为:,
放学回家的速度为:,
故答案为:5,3;
见答案;
见答案.
【分析】
根据题意和图象中的数据可以求得小亮上学的速度和放学回家的速度;
根据图象中的数据和题意可以求得线段BC所表示的y与x之间的函数关系;
由题意可知,小明从家到超市和从超市到家的时间之和是总的时间减去两次经过超市的时间间隔,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
16.【答案】解:如图:过点A作于M,
,,,,
,
点A的坐标为,点B的坐标为;
作轴于N,如图,
时,直线l恰好过点C,
,
在中,,
点坐标为,
设直线OC的解析式为,
把代入得,解得,
直线OC的解析式为,
设直线OA的解析式为,
把代入得,解得,
直线OA的解析式为,
,
,,
,
即;
设直线AB的解析式为,
把,代入得:,解得,
直线AB的解析式为,
同理可得直线BC的解析式为,
当时,,
若,则,
解得,
此时P点坐标为;
当时,,,
,
若,则,
解得不合题意舍去;
当时,,,
,
若,则,
解得,此时P点坐标为;
综上所述,满足条件的P点坐标为或.
【解析】根据等腰直角三角形的性质即可解决问题;
作轴于N,如图,先利用勾股定理计算出CN得到C点坐标为,再利用待定系数法分别求出直线OC的解析式,直线OA的解析式,则根据一次函数图象上点的坐标特征得到Q、R的坐标,从而得到m关于t的函数关系式;
利用待定系数法求出直线AB的解析式,直线BC的解析式,然后分类讨论:当,,当时,分别列出方程,然后解方程求出t得到P点坐标.
本题是一次函数综合题,考查了等腰直角三角形的性质和一次函数图象上点的坐标特征;会运用待定系数法求一次函数解析式;理解坐标与图形性质,会利用点的坐标表示线段的长;学会运用分类讨论的思想解决数学问题.
17.【答案】解:当时,y与x的函数解析式是;
当时,y与x的函数解析式:,
即;
因为小明家5月份的电费超过元,
所以把代入中,得.
答:小明家5月份用电210度.
【解析】时,电费y就是乘以相应度数;时,电费超过210的度数;
把代入得到的函数解析式中,求解即可.
本题考查一次函数的应用;得到超过210度的电费的计算方式是解决本题的易错点.
18.【答案】解:由题意得,可设函数表达式为:,
把,代入,得,解得,
第一班车离入口处的路程米与时间分的函数表达为;
把代入,解得,
分,
第一班车从入口处到达塔林所需时间10分钟;
设小聪坐上了第n班车,则
,解得,
小聪坐上了第5班车,
等车的时间为5分钟,坐班车所需时间为:分,
步行所需时间:分,
分,
比他在塔林游玩结束后立即步行到草甸提早了7分钟.
【解析】设,运用待定系数法求解即可;
把代入的结论即可;
设小聪坐上了第n班车,,解得,可得小聪坐上了第5班车,再根据“路程、速度与时间的关系”解答即可.
本题主要考查了一次函数的应用,熟练掌握待定系数法求出函数解析式是解答本题的关键.
第2页,共18页
第1页,共18页
