角的比较（共19张ppt）

(共19张PPT)
复习：判断（概念要清）
1、两条射线组成的图形叫做角。
2、平角是一条直线。
3、周角是一条射线。
4、大于90度的角是钝角。
5、周角的一半是平角。
6、18°15`和18.15°相等。
(√)
(×)
(×)
(×)
(×)
(×)
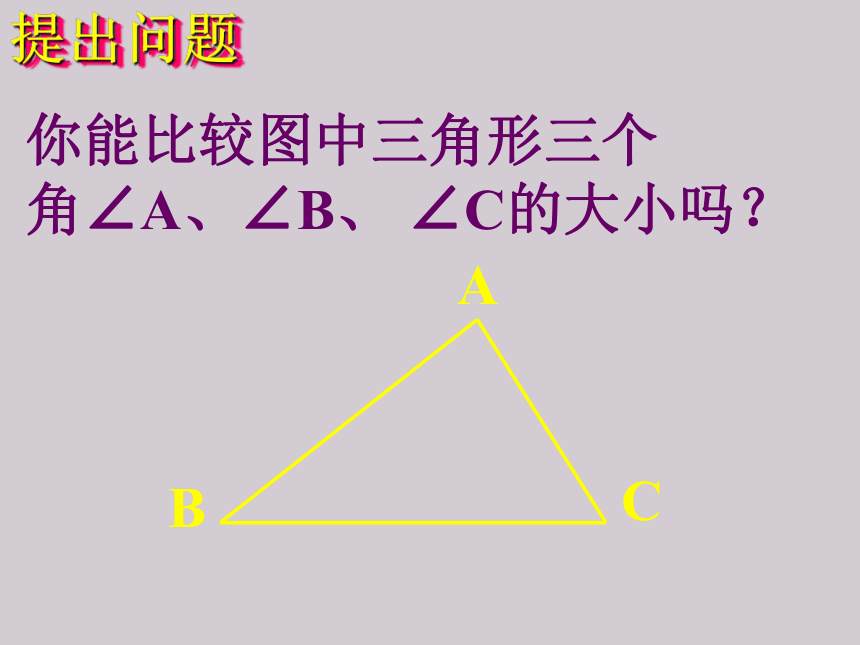
提出问题
你能比较图中三角形三个
角∠A、∠B、
∠C的大小吗？
A
B
C
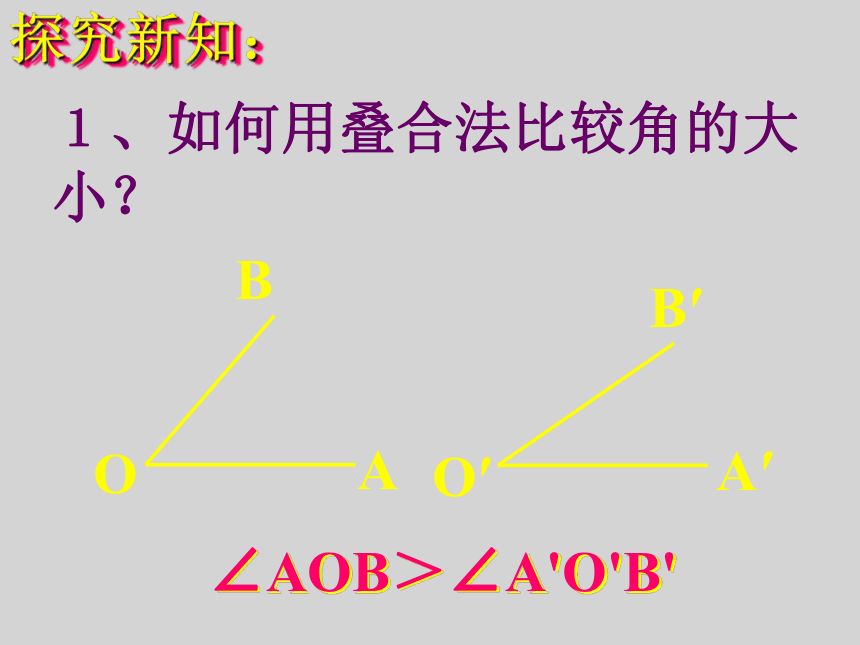
探究新知：
１、如何用叠合法比较角的大小？
O
B
A
O′
B′
A′
∠AOB＞∠A'O'B'
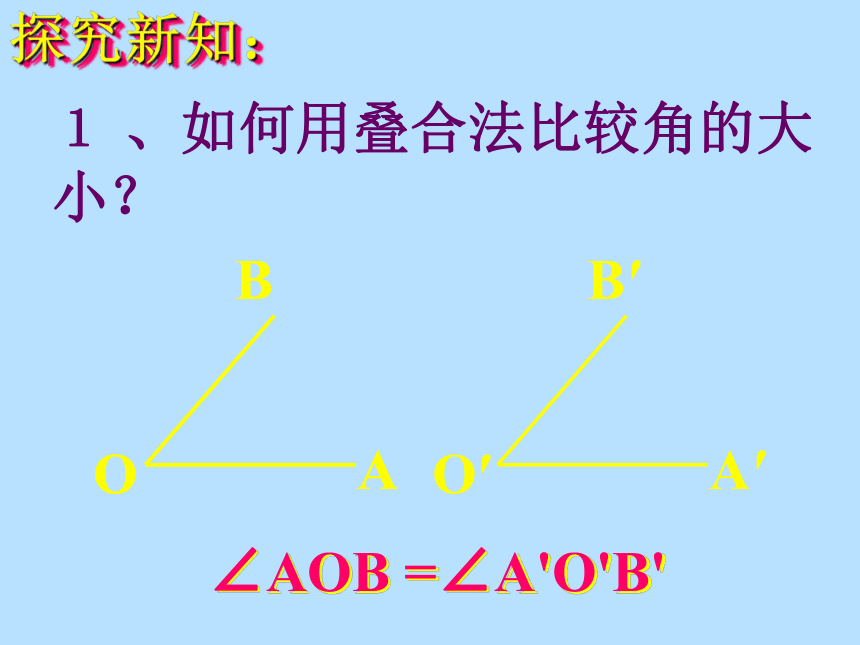
探究新知：
１
、如何用叠合法比较角的大小？
O
B
A
O
B
A
O′
B′
A′
∠AOB
=∠A'O'B'
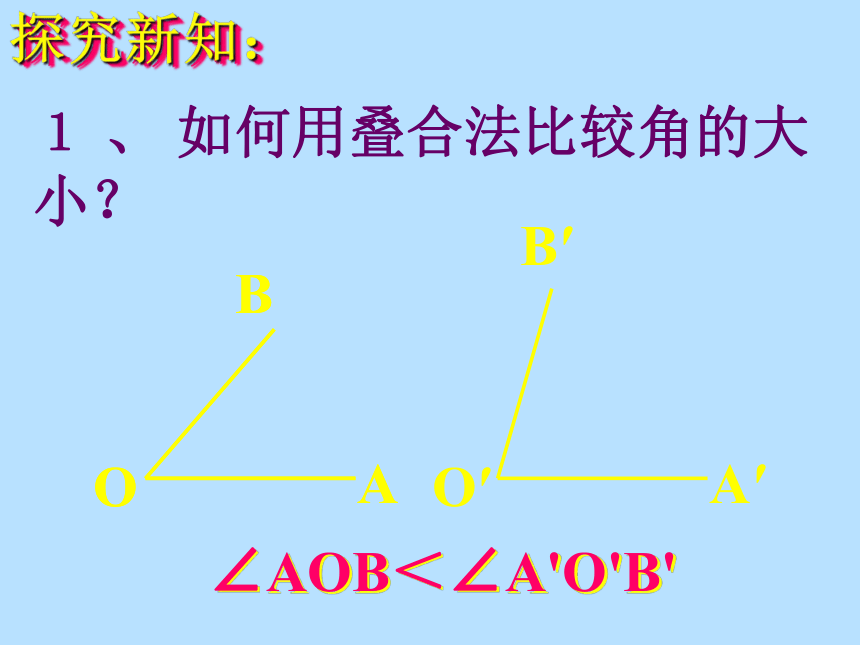
探究新知：
１
、
如何用叠合法比较角的大小？
O
B
A
O
B
A
O′
B′
A′
∠AOB＜∠A'O'B'
一、角的比较
1、用叠合法比较角的大小
2、用度量法比较角的大小
※角的大小与边的长短无关。
在放大镜下一个角变大了吗？
探究新知：
２、怎样进行两角相加？
1
2
2
∠1+∠2
探究新知：
２、怎样进行两角相减？
1
2
∠1―∠2
2
练习
2、借助三角尺，画出15°、
75°的角。
做一做：将一个角对折，使两边重合，折痕与角两边所成的两个角的大小有什么关系？
二、角平分线
表达式：如图
∵射线OC平分∠AOB
∴
O
A
B
C
∠AOB=2∠AOC=2
∠
COB
∠
AOC=
∠
COB
=
∠
AOB
从角的顶点出发引出的一条直线，把这个角分成两个相等的角的射线叫做角的平分线。
反之：如图
∵∠
AOC=
∠
COB
=
∠
AOB
∴射线OC平分∠AOB
练习：P133
2、
三、角的和、差、倍、分
角的和、差、倍、分的度数等于它们的度数的和、差、倍、分
例1、根据右图，求解下列问题：
（1）
比较∠AOB，
∠AOD，
∠AOE，的大小，并指出其中
的锐角、直角、鈍角、平角。
（2）写出∠AOB，
∠AOC，
∠BOC，
∠AOE中某些角之间的两个等量关系
例1.如图
∠AOB+
∠BOD=
；
∠AOC+
∠COD=
；
∠BOC=
∠AOC
-
；
∠AOC+
∠BOD=
∠AOD+
；
∠AOD-
∠AOB-
∠COD=
。
O
A
B
C
D
∠AOD
∠AOD
∠AOB
∠BOC
∠BOC
用一副三角板还可以画出哪些特殊的角？
30°45°60°90°
15°75°105°120°
150°165°195…
例2.如图，已知OB是∠
AOC的平分线，OD是∠
COE的平分线，如果
∠AOE=130°，求∠
BOD的度数
O
A
B
C
D
E
例3.如图，∠AOC=
∠COD
=
∠BOD，则
∠BOC的平分线是
，
3
∠COD
=
，
∠AOB
=
,
∠AOB的三等分线是
。
O
A
B
C
D
OD
∠AOB
∠AOC=
∠COD
=∠BOD
OD、OC
例4.如图，OC是∠DOE和∠AOB的平分线，说明∠AOD
=
∵OC平分∠
AOB
∴
∠AOC=________
∵OC平分∠DOE
∴
=
_________
∴
∠AOC-
∠
DOC=
∠
COB-
∠
COE
（等式性质）
即
=
。
∠BOC
∠DOC
∠COE
∠AOD
∠BOE
∠BOE
五分钟测试；
如图，直线AB、CD交于点O，
且∠
BOC=80
°，
OE平分∠
BOC
，
OF为OE的反向延长线。
（1）求∠2，∠
3的度数；
（2）OF平分∠
AOD吗？为什么？
同理
∠AOF=180°-∠1-∠2
=40°
∴∠AOF=∠3
°
∵∠COD是平角，
∠BOC=80°
∴∠1=
∠BOC=40°
∴
∠2=∠COD-∠COB=180-
80°=100°
∵OE平分∠
COB
∴
∠3
=
180°-∠1-∠2
=40°
∴OF平分∠
AOD
课堂小结：
1、角的比较
（1）用叠合法（2）用度量法
2、角的和、差、倍、
3、角平分线定义：从一个角的顶点的射线把这个角分成两个相等的角，这条射线叫做这个角的平分线
4、角的平分线的三种表示方法