华东师大版九年级数学上册 第24章 解直角三角形 单元测试题(Word版 含解析)
文档属性
| 名称 | 华东师大版九年级数学上册 第24章 解直角三角形 单元测试题(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 287.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览


文档简介
1061720010744200123190000第24章 解直角三角形 单元测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. tan30?=( )
A.1 B.22 C.33 D.3
?
2. 如图,在Rt△ABC中,∠ACB=90?,CD⊥AB,垂足为D.下列结论中,不一定成立的是( )
A.∠A与∠1互余 B.∠B与∠2互余 C.∠A=∠2 D.∠1=∠2
?
3. 如图,sinA等于( )
A.2 B.55 C.12 D.5
?
4. △ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于点D,若BC=a,则CD等于( )
A.12a B.32a C.32a D.3a
?
5. Rt△ABC中,∠C=90?,若AB=4,∠A=θ,则AC的长为(? ? ? ? )
A.4sinθ B.4cosθ C.4sinθ D.4cosθ
?
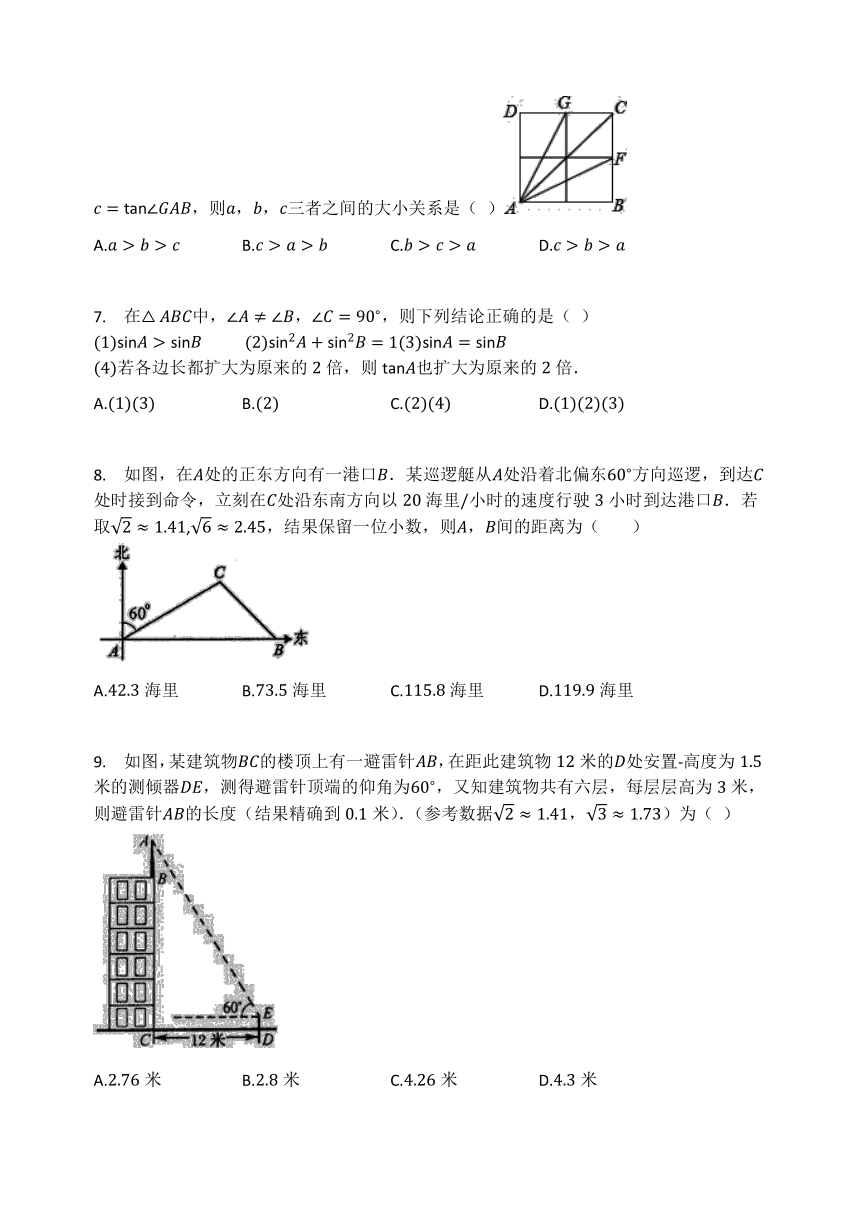
6. 如图,F,G分别为正方形ABCD的边BC,CD的中点,若设a=cos∠FAB,b=sin∠CAB,c=tan∠GAB,则a,b,c三者之间的大小关系是( )
A.a>b>c B.c>a>b C.b>c>a D.c>b>a
?
7. 在△ABC中,∠A≠∠B,∠C=90?,则下列结论正确的是( )
(1)sinA>sinB???????????(2)sin2A+sin2B=1(3)sinA=sinB
(4)若各边长都扩大为原来的2倍,则tanA也扩大为原来的2倍.
A.(1)(3) B.(2) C.(2)(4) D.(1)(2)(3)
?
8. 如图,在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60?方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.若取2≈1.41,6≈2.45,结果保留一位小数,则A,B间的距离为(????????)
A.42.3海里 B.73.5海里 C.115.8海里 D.119.9海里
?
9. 如图,某建筑物BC的楼顶上有一避雷针AB,在距此建筑物12米的D处安置-高度为1.5米的测倾器DE,测得避雷针顶端的仰角为60?,又知建筑物共有六层,每层层高为3米,则避雷针AB的长度(结果精确到0.1米).(参考数据2≈1.41,3≈1.73)为( )
A.2.76米 B.2.8米 C.4.26米 D.4.3米
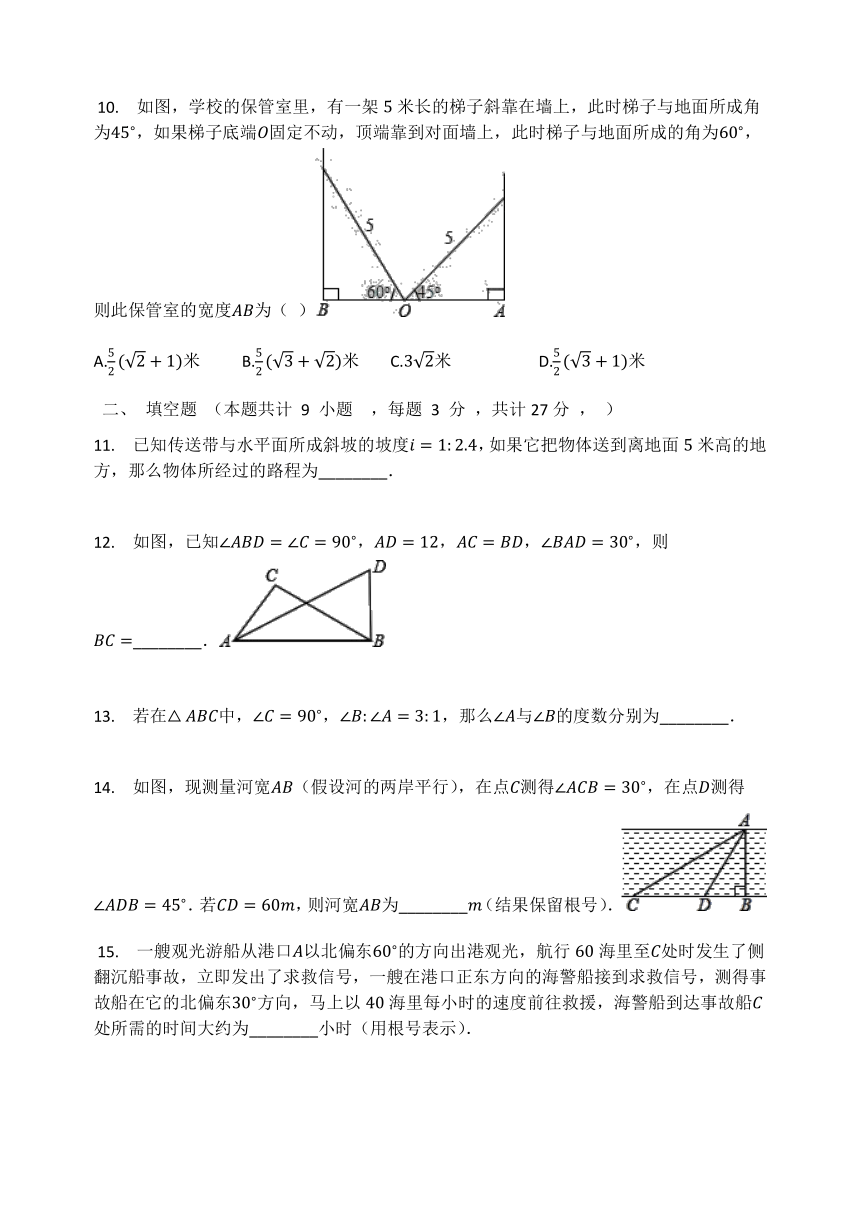
?10. 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成角为45?,如果梯子底端O固定不动,顶端靠到对面墙上,此时梯子与地面所成的角为60?,则此保管室的宽度AB为( )
A.52(2+1)米 B.52(3+2)米 C.32米 D.52(3+1)米
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
11. 已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面5米高的地方,那么物体所经过的路程为________.
?
12. 如图,已知∠ABD=∠C=90?,AD=12,AC=BD,∠BAD=30?,则BC=________.
?
13. 若在△ABC中,∠C=90?,∠B:∠A=3:1,那么∠A与∠B的度数分别为________.
?
14. 如图,现测量河宽AB(假设河的两岸平行),在点C测得∠ACB=30?,在点D测得∠ADB=45?.若CD=60m,则河宽AB为________m(结果保留根号).
?15. 一艘观光游船从港口A以北偏东60?的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30?方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为________小时(用根号表示).
?
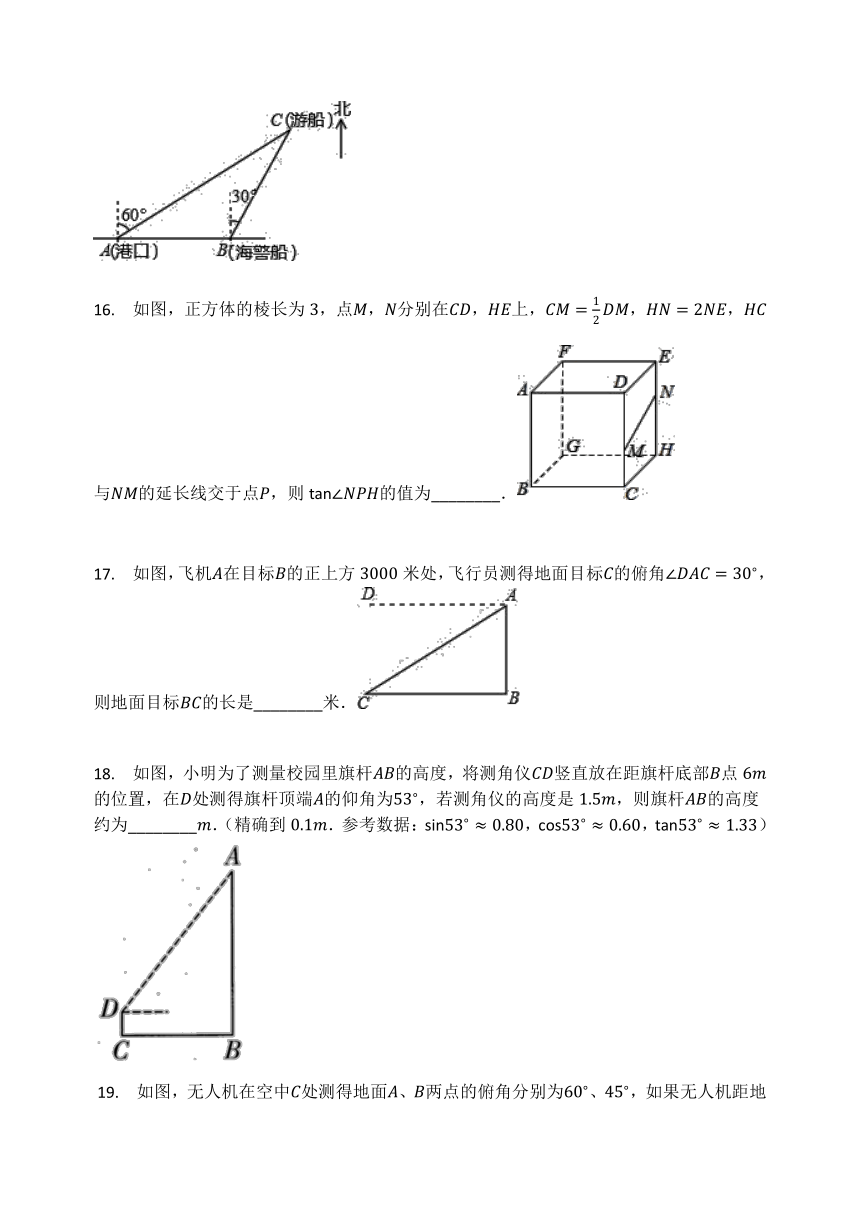
16. 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=12DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为________.
?
17. 如图,飞机A在目标B的正上方3000米处,飞行员测得地面目标C的俯角∠DAC=30?,则地面目标BC的长是________米.
?
18. 如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53?,若测角仪的高度是1.5m,则旗杆AB的高度约为________m.(精确到0.1m.参考数据:sin53?≈0.80,cos53?≈0.60,tan53?≈1.33)
?19. 如图,无人机在空中C处测得地面A、B两点的俯角分别为60?、45?,如果无人机距地面高度CD为90米,点A、D、B在同一水平直线上,则A、B两点间的距离是________米.(结果保留根号)
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
20. 如图,在△ABC中,∠ACB=90?,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55?.求∠A的度数.
?
21. 如图,某水库堤坝横断面迎水坡AB的坡比(也叫坡度)是1:3,堤坝高BC=50m,求迎水坡面AB的长度.
?
22. 如图,一轮船由西向东以20海里/时的速度航行,在A处测得小岛P在北偏东75?方向,1.5小时后,轮船在B处测得小岛P在北偏东60?方向,已知小岛P周围12海里范围内有暗礁.若轮船继续向前航行,有没有触礁的危险?为什么?
?
23. 小明想利用小区附近的楼房来测同一水平线上一棵树的高度.如图,他在同一水平线上选择了一点A,使A与树顶E,楼房顶点D也恰好在一条直线上.小明测得A处的仰角为∠A=30?.已知楼房CD高21米,且与树BE之间的距离BC=30米,求此树的高度约为多少米?(结果保留两个有效数字,3≈1.732).
24. 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸MN//PQ,小聪在河岸MN上的点A处用测角仪测得河对岸小树D位于南偏东45?方向,然后沿河岸走了40米到达B处,测得河对岸电线杆C位于南偏西60?方向 ,此时,其他同学测得CD=120米.请根据这些数据求出河的宽度.(结果保留根号)?
?25. 为解决郑州交通拥堵的问题,政府决定北在A、D两地修建高架路,为此,公交车不得不更改线路,原来直接由A到D的公交车现改为由A-B-C-D,如图,其中A、B、C三地在同一直线上,D地在A地北偏东45?方向,在B地正北方向,在C地北偏西60?方向.C地在A地北偏东75?方向,B、D两地相距2km.问更改线路后公交车多行了多远?(结果保留整数,参考数据:2≈1.4,3≈1.7)
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:tan30?=33.
故选C.
2.
【答案】
D
【解答】
解:A、在Rt△ACD中,∠ADC=90?,所以∠A与∠1互余,正确;
B、在Rt△BCD中,∠BDC=90?,所以∠B与∠2互余,正确;
C、∵ ∠A+∠1=90?,∠1+∠2=90?,
∴ ∠A=∠2,正确;
D、当∠A=∠B时,AC=AB,所以CD既是∠C的角平分线,也是斜边上的高与中线,所以∠1=∠2,正确;当∠A≠∠B时,∠1≠∠2,错误;
故选D.
3.
【答案】
C
【解答】
解:sinA=12,
故选:C.
4.
【答案】
B
【解答】
解:已知△ABC中,∠A:∠B:∠C=l:2:3,
∴ ∠A=180×11+2+3=30?,
∠B=180?×21+2+3=60?,
∠ACB=180?×31+2+3=90?,
又∵ CD⊥AB,
∴ 在Rt△BCD中,
CD=BC?sin∠B=32a.
故选B.
5.
【答案】
B
【解答】
解:Rt△ABC中,∠C=90?,若AB=4,∠A=θ,
cosA=ACAB,
∴ AC=4cosθ.
故选B.
6.
【答案】
B
【解答】
解:设其中每个小正方形的边长是单位1.
根据锐角三角函数的概念,得
a=ABAF=25=255,b=sin45?=22,c=ADDG=2,
显然c>a>b.
故选B.
7.
【答案】
B
【解答】
解:如图:
∵ 当∠A=30?,∠B=60?时,sinA∵ sin2A+sin2B=(BCAB)2+(ACAB)2=BC2AB2+AC2AB2=BC2+AC2AB2=1,∴ (2)正确;
∵ sinA=BCAB,sinB=ACAB,∴ (3)错误;
∵ 若各边长都扩大为原来的2倍,则tanA的值不变,∴ (4)错误;
故选B.
8.
【答案】
C
【解答】
解:如图,过点C作CD⊥?AB于D.
由题意可得,∠DCB=∠CBD=45?,∠CAD=30?,BC=3×20=60(海里),
∴ 在直角△CDB中,BD=CD=22BC=302(海里).
在直角△CDA中,CDAD=tan30?=33,
∴ AD=306(海里),
∴ AB=AD+BD=306+302≈30×2.45+30×1.41≈115.8(海里).
故选C.
9.
【答案】
D
【解答】
解:过点E作EM⊥AC.
在直角△AEM中,AM=ME?tan60?=123,
∴ AC=123+1.5≈22.26,BC=6×3=18.
∴ AB=AC-BC=4.26≈4.3(米).
故选D.
10.
【答案】
A
【解答】
解:由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵ cos45?=AO5=22,
∴ AO=522;
而cos60?=BO5=12,
∴ BO=52.
∴ AB=AO+BO=52+52=52(2+1).
故选A.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
11.
【答案】
13m
【解答】
解:如图,由题意得:斜坡AB的坡度:i=1:2.4,AE=5米,AE⊥BD,
∵ i=AEBE=12.4,
∴ BE=12米,
∴ 在Rt△ABE中,AB=AE2+BE2=13(米).
故答案为:13m.
12.
【答案】
62
【解答】
解:已知∠ABD=∠C=90?,AD=12,AC=BD,∠BAD=30?,
∴ BD=12AD=12×12=6,
∴ AC=BD=6,
在直角三角形ABD中,根据勾股定理得:
AB=AD2-BD2=122-62=63,
在直角三角形ACB中,根据勾股定理得:
BC=AB2-AC2=(63)2-62=62.
故答案为:62.
13.
【答案】
22.5?,67.5?
【解答】
解:∵ ∠B:∠A=3:1,
∴ 设∠B=3k,∠A=k,
∵ ∠C=90?,
∴ ∠B+∠A=90?,
即3k+k=90?,
解得k=22.5?,
∴ ∠A=22.5?,∠B=3×22.5?=67.5?.
故答案为:22.5?,67.5?.
14.
【答案】
30+303
【解答】
解:设AB=xm,
∵ ∠ADB=45?,
∴ BD=AB=xm,
∴ BC=CD+BD=(60+x)m.
∵ ∠ACB=30?,
∴ tan30?=ABCD+BD=xx+60=33,解得x=30+303
∴ AB=(30+303)m.
故答案为:(30+303)m
15.
【答案】
32
【解答】
如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,
∵ ∠ADC=90?,∠CAD=30?,AC=60海里,
∴ CD=12AC=30海里.
在Rt△CBD中,
∵ ∠CDB=90?,∠CBD=90?-37?=53?,
∴ BC=CDsin∠CBD=3032=203(海里),
∴ 海警船到大事故船C处所需的时间大约为:203÷40=32(小时).
16.
【答案】
13
【解答】
解:∵ 正方体的棱长为3,点M,N分别在CD,HE上,CM=12DM,HN=2NE,
∴ MC=1,HN=2,
∵ DC?//?EH,
∴ PCPH=MCNH=12,
∵ HC=3,
∴ PC=3,
∴ PH=6,
∴ tan∠NPH=NHPH=26=13,
故答案为:13.
17.
【答案】
30003
【解答】
解:根据题意可得:BC=AB÷tan30?=30003(米).
18.
【答案】
9.5
【解答】
此题暂无解答
19.
【答案】
(303+90)
【解答】
根据题意可知:
∠CAD=60?,∠CBD=45?,CD=90,
∴ 在Rt△ACD中,AD=CDtan60=303,
在Rt△BCD中,BD=CD=90,
∴ AB=AD+BD=303+90.
所以A、B两点间的距离是(303+90)米.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
20.
【答案】
解:∵ FD⊥AB于D,
∴ ∠BED+∠B=90?,
∵ ∠ACB=90?,
∴ ∠A+∠B=90?,
∴ ∠A=∠BED=55?.
【解答】
解:∵ FD⊥AB于D,
∴ ∠BED+∠B=90?,
∵ ∠ACB=90?,
∴ ∠A+∠B=90?,
∴ ∠A=∠BED=55?.
21.
【答案】
解:∵ 堤坝横断面迎水坡AB的坡比是1:3,
∴ BCAC=33,
∵ BC=50m,
∴ AC=503m,
∴ AB=AC2+CB2=100m,
∴ 迎水坡面AB的长度为100m.
【解答】
解:∵ 堤坝横断面迎水坡AB的坡比是1:3,
∴ BCAC=33,
∵ BC=50m,
∴ AC=503m,
∴ AB=AC2+CB2=100m,
∴ 迎水坡面AB的长度为100m.
22.
【答案】
解:作辅助线PD⊥AB于D,
∵ A处测得小岛P在北偏东75?方向,
∴ ∠PAB=15?,
∵ 在B处测得小岛P在北偏东60?方向,
∴ ∠APB=15?,
∴ AB=PB,
∵ AB=20×1.5=30海里,
∴ PB=30海里,
∵ ∠PBD=∠PAB+∠BPA,
∴ ∠PBD=30?,
∴ PD=15>12,
∴ 船不改变航向,不会触礁.
【解答】
解:作辅助线PD⊥AB于D,
∵ A处测得小岛P在北偏东75?方向,
∴ ∠PAB=15?,
∵ 在B处测得小岛P在北偏东60?方向,
∴ ∠APB=15?,
∴ AB=PB,
∵ AB=20×1.5=30海里,
∴ PB=30海里,
∵ ∠PBD=∠PAB+∠BPA,
∴ ∠PBD=30?,
∴ PD=15>12,
∴ 船不改变航向,不会触礁.
23.
【答案】
解:根据题意可得:
AC=DCtan30?=2133=213(米).
则AB=AC-BC=213-30(米),
故树高BE=AB×tan30?=(213-30)×tan30?≈3.7(米).
【解答】
解:根据题意可得:
AC=DCtan30?=2133=213(米).
则AB=AC-BC=213-30(米),
故树高BE=AB×tan30?=(213-30)×tan30?≈3.7(米).
24.
【答案】
解:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,如图.
∴ ∠ECB=60?,∠FDA=45?,
四边形CEFD是矩形.
设CE=DF=x米,
在Rt?△CEB中,BE=CE?tan60?=3x米.
在Rt△DFA中,AF=DF=x米.
∵ EF=CD=120米,
∴ 3x+x-40=120,
解得x=80(3-1).
答:河的宽度为80(3-1)米.
【解答】
解:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,如图.
∴ ∠ECB=60?,∠FDA=45?,
四边形CEFD是矩形.
设CE=DF=x米,
在Rt?△CEB中,BE=CE?tan60?=3x米.
在Rt△DFA中,AF=DF=x米.
∵ EF=CD=120米,
∴ 3x+x-40=120,
解得x=80(3-1).
答:河的宽度为80(3-1)米.
25.
【答案】
更改线路后公交车多行了4km.
【解答】
解:过B作BH⊥AD于H.
依题意∠BDH=45?,∠CBD=75?,∠BAD=75?-45?=30?.
在Rt△BDH中,HD=BH=BD?cos45?=2,
在Rt△ABH中,AH=BHtan30?=6,
AB=BHsin30?=22,
∴ AD=AH+HD=6+2.
∵ ∠ABD=180?-75?=105?,
∴ ∠ADC=45?+60?=105?,
∴ ∠ABD=∠ADC.
又∠DAB=∠CAD,
∴ △ABD∽△ADC,
∴ ADAC=BDCD=ABAD,即6+2AC=2CD=226+2,
解得:AC=22+6,CD=3+1.
∴ AC+CD-AD=22+6+3+1-6-2=2+3+1≈4(km).
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. tan30?=( )
A.1 B.22 C.33 D.3
?
2. 如图,在Rt△ABC中,∠ACB=90?,CD⊥AB,垂足为D.下列结论中,不一定成立的是( )
A.∠A与∠1互余 B.∠B与∠2互余 C.∠A=∠2 D.∠1=∠2
?
3. 如图,sinA等于( )
A.2 B.55 C.12 D.5
?
4. △ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于点D,若BC=a,则CD等于( )
A.12a B.32a C.32a D.3a
?
5. Rt△ABC中,∠C=90?,若AB=4,∠A=θ,则AC的长为(? ? ? ? )
A.4sinθ B.4cosθ C.4sinθ D.4cosθ
?
6. 如图,F,G分别为正方形ABCD的边BC,CD的中点,若设a=cos∠FAB,b=sin∠CAB,c=tan∠GAB,则a,b,c三者之间的大小关系是( )
A.a>b>c B.c>a>b C.b>c>a D.c>b>a
?
7. 在△ABC中,∠A≠∠B,∠C=90?,则下列结论正确的是( )
(1)sinA>sinB???????????(2)sin2A+sin2B=1(3)sinA=sinB
(4)若各边长都扩大为原来的2倍,则tanA也扩大为原来的2倍.
A.(1)(3) B.(2) C.(2)(4) D.(1)(2)(3)
?
8. 如图,在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60?方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.若取2≈1.41,6≈2.45,结果保留一位小数,则A,B间的距离为(????????)
A.42.3海里 B.73.5海里 C.115.8海里 D.119.9海里
?
9. 如图,某建筑物BC的楼顶上有一避雷针AB,在距此建筑物12米的D处安置-高度为1.5米的测倾器DE,测得避雷针顶端的仰角为60?,又知建筑物共有六层,每层层高为3米,则避雷针AB的长度(结果精确到0.1米).(参考数据2≈1.41,3≈1.73)为( )
A.2.76米 B.2.8米 C.4.26米 D.4.3米
?10. 如图,学校的保管室里,有一架5米长的梯子斜靠在墙上,此时梯子与地面所成角为45?,如果梯子底端O固定不动,顶端靠到对面墙上,此时梯子与地面所成的角为60?,则此保管室的宽度AB为( )
A.52(2+1)米 B.52(3+2)米 C.32米 D.52(3+1)米
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , ) ?
11. 已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面5米高的地方,那么物体所经过的路程为________.
?
12. 如图,已知∠ABD=∠C=90?,AD=12,AC=BD,∠BAD=30?,则BC=________.
?
13. 若在△ABC中,∠C=90?,∠B:∠A=3:1,那么∠A与∠B的度数分别为________.
?
14. 如图,现测量河宽AB(假设河的两岸平行),在点C测得∠ACB=30?,在点D测得∠ADB=45?.若CD=60m,则河宽AB为________m(结果保留根号).
?15. 一艘观光游船从港口A以北偏东60?的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30?方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为________小时(用根号表示).
?
16. 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=12DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为________.
?
17. 如图,飞机A在目标B的正上方3000米处,飞行员测得地面目标C的俯角∠DAC=30?,则地面目标BC的长是________米.
?
18. 如图,小明为了测量校园里旗杆AB的高度,将测角仪CD竖直放在距旗杆底部B点6m的位置,在D处测得旗杆顶端A的仰角为53?,若测角仪的高度是1.5m,则旗杆AB的高度约为________m.(精确到0.1m.参考数据:sin53?≈0.80,cos53?≈0.60,tan53?≈1.33)
?19. 如图,无人机在空中C处测得地面A、B两点的俯角分别为60?、45?,如果无人机距地面高度CD为90米,点A、D、B在同一水平直线上,则A、B两点间的距离是________米.(结果保留根号)
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
20. 如图,在△ABC中,∠ACB=90?,F是AC延长线上一点,FD⊥AB,垂足为D,FD与BC相交于点E,∠BED=55?.求∠A的度数.
?
21. 如图,某水库堤坝横断面迎水坡AB的坡比(也叫坡度)是1:3,堤坝高BC=50m,求迎水坡面AB的长度.
?
22. 如图,一轮船由西向东以20海里/时的速度航行,在A处测得小岛P在北偏东75?方向,1.5小时后,轮船在B处测得小岛P在北偏东60?方向,已知小岛P周围12海里范围内有暗礁.若轮船继续向前航行,有没有触礁的危险?为什么?
?
23. 小明想利用小区附近的楼房来测同一水平线上一棵树的高度.如图,他在同一水平线上选择了一点A,使A与树顶E,楼房顶点D也恰好在一条直线上.小明测得A处的仰角为∠A=30?.已知楼房CD高21米,且与树BE之间的距离BC=30米,求此树的高度约为多少米?(结果保留两个有效数字,3≈1.732).
24. 在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸MN//PQ,小聪在河岸MN上的点A处用测角仪测得河对岸小树D位于南偏东45?方向,然后沿河岸走了40米到达B处,测得河对岸电线杆C位于南偏西60?方向 ,此时,其他同学测得CD=120米.请根据这些数据求出河的宽度.(结果保留根号)?
?25. 为解决郑州交通拥堵的问题,政府决定北在A、D两地修建高架路,为此,公交车不得不更改线路,原来直接由A到D的公交车现改为由A-B-C-D,如图,其中A、B、C三地在同一直线上,D地在A地北偏东45?方向,在B地正北方向,在C地北偏西60?方向.C地在A地北偏东75?方向,B、D两地相距2km.问更改线路后公交车多行了多远?(结果保留整数,参考数据:2≈1.4,3≈1.7)
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:tan30?=33.
故选C.
2.
【答案】
D
【解答】
解:A、在Rt△ACD中,∠ADC=90?,所以∠A与∠1互余,正确;
B、在Rt△BCD中,∠BDC=90?,所以∠B与∠2互余,正确;
C、∵ ∠A+∠1=90?,∠1+∠2=90?,
∴ ∠A=∠2,正确;
D、当∠A=∠B时,AC=AB,所以CD既是∠C的角平分线,也是斜边上的高与中线,所以∠1=∠2,正确;当∠A≠∠B时,∠1≠∠2,错误;
故选D.
3.
【答案】
C
【解答】
解:sinA=12,
故选:C.
4.
【答案】
B
【解答】
解:已知△ABC中,∠A:∠B:∠C=l:2:3,
∴ ∠A=180×11+2+3=30?,
∠B=180?×21+2+3=60?,
∠ACB=180?×31+2+3=90?,
又∵ CD⊥AB,
∴ 在Rt△BCD中,
CD=BC?sin∠B=32a.
故选B.
5.
【答案】
B
【解答】
解:Rt△ABC中,∠C=90?,若AB=4,∠A=θ,
cosA=ACAB,
∴ AC=4cosθ.
故选B.
6.
【答案】
B
【解答】
解:设其中每个小正方形的边长是单位1.
根据锐角三角函数的概念,得
a=ABAF=25=255,b=sin45?=22,c=ADDG=2,
显然c>a>b.
故选B.
7.
【答案】
B
【解答】
解:如图:
∵ 当∠A=30?,∠B=60?时,sinA
∵ sinA=BCAB,sinB=ACAB,∴ (3)错误;
∵ 若各边长都扩大为原来的2倍,则tanA的值不变,∴ (4)错误;
故选B.
8.
【答案】
C
【解答】
解:如图,过点C作CD⊥?AB于D.
由题意可得,∠DCB=∠CBD=45?,∠CAD=30?,BC=3×20=60(海里),
∴ 在直角△CDB中,BD=CD=22BC=302(海里).
在直角△CDA中,CDAD=tan30?=33,
∴ AD=306(海里),
∴ AB=AD+BD=306+302≈30×2.45+30×1.41≈115.8(海里).
故选C.
9.
【答案】
D
【解答】
解:过点E作EM⊥AC.
在直角△AEM中,AM=ME?tan60?=123,
∴ AC=123+1.5≈22.26,BC=6×3=18.
∴ AB=AC-BC=4.26≈4.3(米).
故选D.
10.
【答案】
A
【解答】
解:由于两边的墙都和地面垂直,所以构成了两个直角三角形.
∵ cos45?=AO5=22,
∴ AO=522;
而cos60?=BO5=12,
∴ BO=52.
∴ AB=AO+BO=52+52=52(2+1).
故选A.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
11.
【答案】
13m
【解答】
解:如图,由题意得:斜坡AB的坡度:i=1:2.4,AE=5米,AE⊥BD,
∵ i=AEBE=12.4,
∴ BE=12米,
∴ 在Rt△ABE中,AB=AE2+BE2=13(米).
故答案为:13m.
12.
【答案】
62
【解答】
解:已知∠ABD=∠C=90?,AD=12,AC=BD,∠BAD=30?,
∴ BD=12AD=12×12=6,
∴ AC=BD=6,
在直角三角形ABD中,根据勾股定理得:
AB=AD2-BD2=122-62=63,
在直角三角形ACB中,根据勾股定理得:
BC=AB2-AC2=(63)2-62=62.
故答案为:62.
13.
【答案】
22.5?,67.5?
【解答】
解:∵ ∠B:∠A=3:1,
∴ 设∠B=3k,∠A=k,
∵ ∠C=90?,
∴ ∠B+∠A=90?,
即3k+k=90?,
解得k=22.5?,
∴ ∠A=22.5?,∠B=3×22.5?=67.5?.
故答案为:22.5?,67.5?.
14.
【答案】
30+303
【解答】
解:设AB=xm,
∵ ∠ADB=45?,
∴ BD=AB=xm,
∴ BC=CD+BD=(60+x)m.
∵ ∠ACB=30?,
∴ tan30?=ABCD+BD=xx+60=33,解得x=30+303
∴ AB=(30+303)m.
故答案为:(30+303)m
15.
【答案】
32
【解答】
如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,
∵ ∠ADC=90?,∠CAD=30?,AC=60海里,
∴ CD=12AC=30海里.
在Rt△CBD中,
∵ ∠CDB=90?,∠CBD=90?-37?=53?,
∴ BC=CDsin∠CBD=3032=203(海里),
∴ 海警船到大事故船C处所需的时间大约为:203÷40=32(小时).
16.
【答案】
13
【解答】
解:∵ 正方体的棱长为3,点M,N分别在CD,HE上,CM=12DM,HN=2NE,
∴ MC=1,HN=2,
∵ DC?//?EH,
∴ PCPH=MCNH=12,
∵ HC=3,
∴ PC=3,
∴ PH=6,
∴ tan∠NPH=NHPH=26=13,
故答案为:13.
17.
【答案】
30003
【解答】
解:根据题意可得:BC=AB÷tan30?=30003(米).
18.
【答案】
9.5
【解答】
此题暂无解答
19.
【答案】
(303+90)
【解答】
根据题意可知:
∠CAD=60?,∠CBD=45?,CD=90,
∴ 在Rt△ACD中,AD=CDtan60=303,
在Rt△BCD中,BD=CD=90,
∴ AB=AD+BD=303+90.
所以A、B两点间的距离是(303+90)米.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
20.
【答案】
解:∵ FD⊥AB于D,
∴ ∠BED+∠B=90?,
∵ ∠ACB=90?,
∴ ∠A+∠B=90?,
∴ ∠A=∠BED=55?.
【解答】
解:∵ FD⊥AB于D,
∴ ∠BED+∠B=90?,
∵ ∠ACB=90?,
∴ ∠A+∠B=90?,
∴ ∠A=∠BED=55?.
21.
【答案】
解:∵ 堤坝横断面迎水坡AB的坡比是1:3,
∴ BCAC=33,
∵ BC=50m,
∴ AC=503m,
∴ AB=AC2+CB2=100m,
∴ 迎水坡面AB的长度为100m.
【解答】
解:∵ 堤坝横断面迎水坡AB的坡比是1:3,
∴ BCAC=33,
∵ BC=50m,
∴ AC=503m,
∴ AB=AC2+CB2=100m,
∴ 迎水坡面AB的长度为100m.
22.
【答案】
解:作辅助线PD⊥AB于D,
∵ A处测得小岛P在北偏东75?方向,
∴ ∠PAB=15?,
∵ 在B处测得小岛P在北偏东60?方向,
∴ ∠APB=15?,
∴ AB=PB,
∵ AB=20×1.5=30海里,
∴ PB=30海里,
∵ ∠PBD=∠PAB+∠BPA,
∴ ∠PBD=30?,
∴ PD=15>12,
∴ 船不改变航向,不会触礁.
【解答】
解:作辅助线PD⊥AB于D,
∵ A处测得小岛P在北偏东75?方向,
∴ ∠PAB=15?,
∵ 在B处测得小岛P在北偏东60?方向,
∴ ∠APB=15?,
∴ AB=PB,
∵ AB=20×1.5=30海里,
∴ PB=30海里,
∵ ∠PBD=∠PAB+∠BPA,
∴ ∠PBD=30?,
∴ PD=15>12,
∴ 船不改变航向,不会触礁.
23.
【答案】
解:根据题意可得:
AC=DCtan30?=2133=213(米).
则AB=AC-BC=213-30(米),
故树高BE=AB×tan30?=(213-30)×tan30?≈3.7(米).
【解答】
解:根据题意可得:
AC=DCtan30?=2133=213(米).
则AB=AC-BC=213-30(米),
故树高BE=AB×tan30?=(213-30)×tan30?≈3.7(米).
24.
【答案】
解:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,如图.
∴ ∠ECB=60?,∠FDA=45?,
四边形CEFD是矩形.
设CE=DF=x米,
在Rt?△CEB中,BE=CE?tan60?=3x米.
在Rt△DFA中,AF=DF=x米.
∵ EF=CD=120米,
∴ 3x+x-40=120,
解得x=80(3-1).
答:河的宽度为80(3-1)米.
【解答】
解:过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,如图.
∴ ∠ECB=60?,∠FDA=45?,
四边形CEFD是矩形.
设CE=DF=x米,
在Rt?△CEB中,BE=CE?tan60?=3x米.
在Rt△DFA中,AF=DF=x米.
∵ EF=CD=120米,
∴ 3x+x-40=120,
解得x=80(3-1).
答:河的宽度为80(3-1)米.
25.
【答案】
更改线路后公交车多行了4km.
【解答】
解:过B作BH⊥AD于H.
依题意∠BDH=45?,∠CBD=75?,∠BAD=75?-45?=30?.
在Rt△BDH中,HD=BH=BD?cos45?=2,
在Rt△ABH中,AH=BHtan30?=6,
AB=BHsin30?=22,
∴ AD=AH+HD=6+2.
∵ ∠ABD=180?-75?=105?,
∴ ∠ADC=45?+60?=105?,
∴ ∠ABD=∠ADC.
又∠DAB=∠CAD,
∴ △ABD∽△ADC,
∴ ADAC=BDCD=ABAD,即6+2AC=2CD=226+2,
解得:AC=22+6,CD=3+1.
∴ AC+CD-AD=22+6+3+1-6-2=2+3+1≈4(km).
