5.1.1 相交线 课件(共34张ppt)
文档属性
| 名称 | 5.1.1 相交线 课件(共34张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览









文档简介
5.1 相交线
5.1.1 相交线
导入新知
导入新知
导入新知
导入新知
1. 借助两直线相交所形成的角初步理解邻补角、对顶角的概念.
2. 会根据邻补角、对顶角的性质去求一个角的度数.
素养目标
3. 掌握邻补角与对顶角的性质,并能运用它们解
决简单实际问题.
如图,把两根木条用钉子钉在一起,转动其中一根木条,观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗?
探究新知
知识点 1
邻补角与对顶角的定义
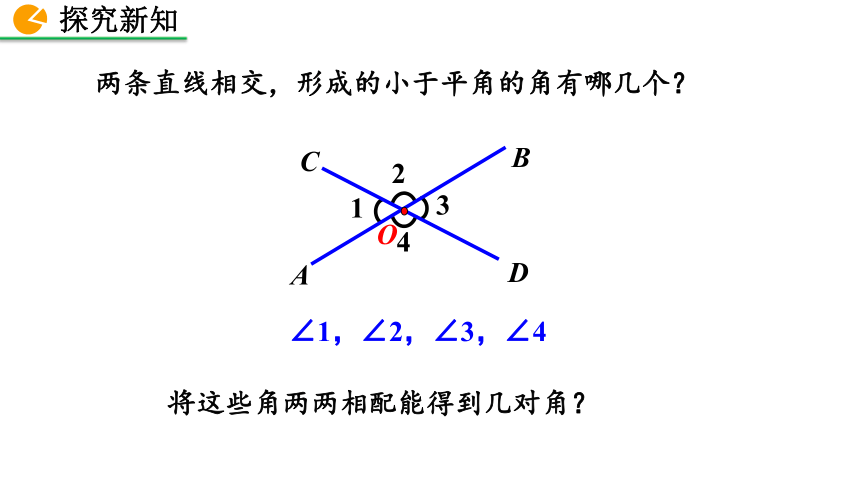
∠1,∠2,∠3,∠4
两条直线相交,形成的小于平角的角有哪几个?
1
2
3
4
B
A
C
D
O
将这些角两两相配能得到几对角?
探究新知
分类
两直线相交
∠1 和∠2
∠2 和∠3
∠1 和∠3
位置关系
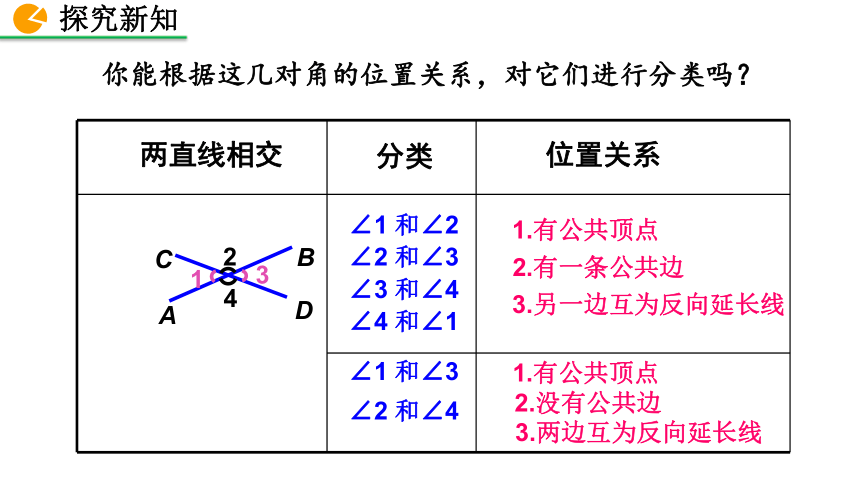
你能根据这几对角的位置关系,对它们进行分类吗?
B
A
C
D
2
4
1
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
探究新知
1.有公共顶点
2.有一条公共边
3.另一边互为反向延长线
1.有公共顶点
2.没有公共边
3.两边互为反向延长线
1
2
3
4
B
C
D
O
A
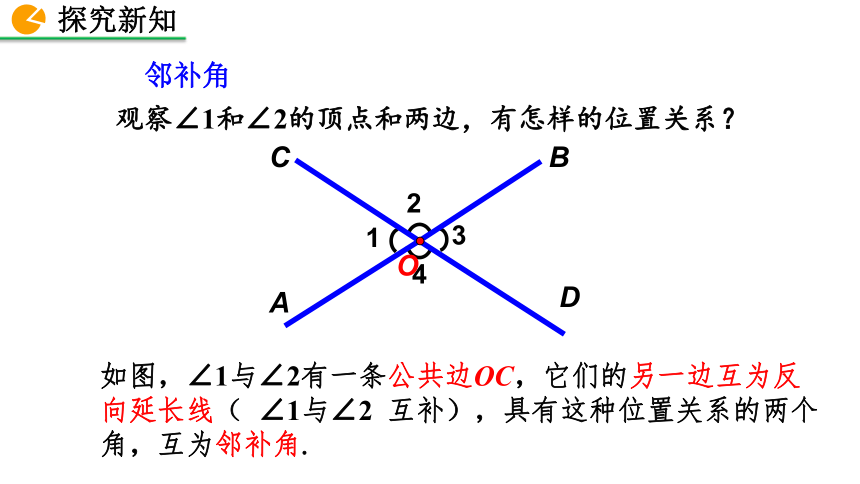
观察∠1和∠2的顶点和两边,有怎样的位置关系?
如图,∠1与∠2有一条公共边OC,它们的另一边互为反向延长线( ∠1与∠2 互补),具有这种位置关系的两个角,互为邻补角.
邻补角
探究新知
1
3
B
C
D
A
2
4
O
类比∠1和∠2,看∠1和∠3有怎样的位置关系?
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
对顶角
探究新知
分类
两直线相交
位置关系
归纳总结
B
A
C
D
2
4
1
3
∠1 和∠2
∠2 和∠3
∠1 和∠3
∠3 和∠4
∠4 和∠1
∠2 和∠4
探究新知
1.有公共顶点
2.有一条公共边
3.另一边互为反向延长线
1.有公共顶点
2.没有公共边
3.两边互为反向延长线
定义
邻补角
对顶角
例 下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
提示:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
探究新知
素养考点 1
对顶角的判断
下列各组角中,∠1与∠2是对顶角的为( )
D
巩固练习
C
O
A
B
D
4
3
2
1
问题:∠1 与∠3在数量上又有什么关系呢?
【讨论】你能利用有关知识来验证∠1与∠3的数量关系吗?
在上学期我们已经知道互为补角的两个角的和为180°,因而互为邻补角的两个角的和为180°.
知识点 2
猜想:对顶角相等.
探究新知
对顶角、领补角的性质
已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3, ∠2=∠4.
证明:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180°,
∴∠1=∠3.
同理可得∠2=∠4.
符号语言:∵直线AB与CD相交于O点,
∴∠1=∠3,∠2=∠4.
探究新知
C
O
A
B
D
4
3
2
1
量一量:图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
探究新知
对顶角相等.
B
A
C
D
O
1
2
3
4
1.有公共顶点
归类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1.有公共顶点
位置关系
邻补角
对顶角
2.有一条公共边
3.另一边互为反向延长线
2.没有公共边
两直线相交
3.两边互为反向延长线
名称
考虑角的位置关系可从角的顶点和角的边入手!
数量关系
对顶
角相
等
邻补
角互
补
探究新知
例1 如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
a
b
)
(
1
3
4
2
)
(
变式1:若∠1= 32°20′,求∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
探究新知
素养考点 1
利用对顶角、领补角的性质求角的度数
解:设∠1=x°,则∠2=3x°,
变式3:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180,
所以 x=45,
根据对顶角相等,可得∠3=∠1=45°.
则∠1=45°,
变式2:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
探究新知
(3)若 ?1: ?2 = 2: 7 ,则∠1,∠2,∠3,∠4的度数分别为________________________.
(2)若∠2是∠3的 3倍,则∠1,∠2,∠3,∠4的度数分别为________________________.
(1)若∠1+∠3= 60? ,则∠1,∠2,∠3,∠4的度数分别为________________________ .
30? 、150? 、30?、150?
45?、 135?、 45?、 135?
40?、140?、40? 、140?
巩固练习
如图所示,直线a和b相交于点O,完成下列各题:
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:∵∠1=40°, ∠BOC=110°(已知),
∴∠BOF=∠BOC-∠1 =110°-40°=70°.
∵∠BOF=∠2(对顶角相等),
∴∠2=70°(等量代换).
提示:隐含条件“对顶角相等”.
探究新知
素养考点 2
利用隐含条件求角的度数
如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ EF与AB相交,∠1+∠2=180°,
∠2+∠3= 180°,
∴∠2的补角有∠1和∠3;
∵ CD与MN相交,∠5+∠8=180°,
∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8;
巩固练习
∴∠2的补角有∠1、∠3、∠6和∠8.
如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3
C.∠2和∠4 D.∠2和∠5
A
连接中考
1.下列各图中∠1、∠2是邻补角吗?为什么?
1
2
1
2
1
2
∠1=140° ∠1=120° ∠1=130°
∠2=40° ∠2=60° ∠2=50°
(1) (2) (3)
不是
不是
是
基础巩固题
课堂检测
2.下列各图中∠1、∠2是对顶角吗?为什么?
1
2
(2)
(3)
(4)
2
1
(1)
2
1
不是
是
不是
不是
(5)
是
1
2
1
2
课堂检测
O
3.如图两堵墙围一个角?AOB,但人不能进入围墙,我们如何去测量这个角的大小呢?
C
D
?AOB=∠COD
?AOB=180°-∠AOC
(邻补角互补)
(对顶角相等)
课堂检测
方法一:
方法二:
A
B
)
)
4.找出图中∠AOE的邻补角及对顶角,若没有请画出.
A
B
C
O
D
E
)
F
解:邻补角是∠EOB和∠AOF;
对顶角是∠BOF.
课堂检测
5.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
C
A
E
D
B
F
O
解:(1)∠AOC的邻补角是∠AOD和∠COB;
∠BOE的邻补角是∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB;
∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°;
∠COB=180°-∠AOC=130°.
课堂检测
6.如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数.
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
课堂检测
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,
找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵∠1= ∠3(对顶角相等),
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°,
∴∠8= ∠1.
∵∠8= ∠6(对顶角相等),
∴∠6= ∠1.
能力提升题
课堂检测
与∠1 相等的角有:∠3、∠8、∠6.
观察下列各图,寻找对顶角(不含平角)
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3) 如图c,图中共有 对对顶角;
(4)研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成 对对顶角;
(5) 若有10条直线相交于一点,则可形成 对对顶角.
图c
2
6
12
n(n-1)
90
拓广探索题
课堂检测
图a
A
B
C
D
O
图b
A
B
C
D
E
F
O
A
B
C
D
E
F
G
H
O
角的
名称
特 征
性 质
相 同 点
不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边.
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边.
①都是两条直线相交而成的角;
③都是成对出现的.
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对.
①有无公共边;
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
5.1.1 相交线
导入新知
导入新知
导入新知
导入新知
1. 借助两直线相交所形成的角初步理解邻补角、对顶角的概念.
2. 会根据邻补角、对顶角的性质去求一个角的度数.
素养目标
3. 掌握邻补角与对顶角的性质,并能运用它们解
决简单实际问题.
如图,把两根木条用钉子钉在一起,转动其中一根木条,观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗?
探究新知
知识点 1
邻补角与对顶角的定义
∠1,∠2,∠3,∠4
两条直线相交,形成的小于平角的角有哪几个?
1
2
3
4
B
A
C
D
O
将这些角两两相配能得到几对角?
探究新知
分类
两直线相交
∠1 和∠2
∠2 和∠3
∠1 和∠3
位置关系
你能根据这几对角的位置关系,对它们进行分类吗?
B
A
C
D
2
4
1
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
探究新知
1.有公共顶点
2.有一条公共边
3.另一边互为反向延长线
1.有公共顶点
2.没有公共边
3.两边互为反向延长线
1
2
3
4
B
C
D
O
A
观察∠1和∠2的顶点和两边,有怎样的位置关系?
如图,∠1与∠2有一条公共边OC,它们的另一边互为反向延长线( ∠1与∠2 互补),具有这种位置关系的两个角,互为邻补角.
邻补角
探究新知
1
3
B
C
D
A
2
4
O
类比∠1和∠2,看∠1和∠3有怎样的位置关系?
如图,∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
对顶角
探究新知
分类
两直线相交
位置关系
归纳总结
B
A
C
D
2
4
1
3
∠1 和∠2
∠2 和∠3
∠1 和∠3
∠3 和∠4
∠4 和∠1
∠2 和∠4
探究新知
1.有公共顶点
2.有一条公共边
3.另一边互为反向延长线
1.有公共顶点
2.没有公共边
3.两边互为反向延长线
定义
邻补角
对顶角
例 下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
提示:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
探究新知
素养考点 1
对顶角的判断
下列各组角中,∠1与∠2是对顶角的为( )
D
巩固练习
C
O
A
B
D
4
3
2
1
问题:∠1 与∠3在数量上又有什么关系呢?
【讨论】你能利用有关知识来验证∠1与∠3的数量关系吗?
在上学期我们已经知道互为补角的两个角的和为180°,因而互为邻补角的两个角的和为180°.
知识点 2
猜想:对顶角相等.
探究新知
对顶角、领补角的性质
已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3, ∠2=∠4.
证明:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180°,
∴∠1=∠3.
同理可得∠2=∠4.
符号语言:∵直线AB与CD相交于O点,
∴∠1=∠3,∠2=∠4.
探究新知
C
O
A
B
D
4
3
2
1
量一量:图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
探究新知
对顶角相等.
B
A
C
D
O
1
2
3
4
1.有公共顶点
归类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1.有公共顶点
位置关系
邻补角
对顶角
2.有一条公共边
3.另一边互为反向延长线
2.没有公共边
两直线相交
3.两边互为反向延长线
名称
考虑角的位置关系可从角的顶点和角的边入手!
数量关系
对顶
角相
等
邻补
角互
补
探究新知
例1 如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数.
a
b
)
(
1
3
4
2
)
(
变式1:若∠1= 32°20′,求∠2、∠3、∠4的度数.
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°;
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°.
探究新知
素养考点 1
利用对顶角、领补角的性质求角的度数
解:设∠1=x°,则∠2=3x°,
变式3:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180,
所以 x=45,
根据对顶角相等,可得∠3=∠1=45°.
则∠1=45°,
变式2:若∠1+∠3 = 50°,则∠3= ,
∠2= .
25°
155°
a
b
)
(
1
3
4
2
)
(
探究新知
(3)若 ?1: ?2 = 2: 7 ,则∠1,∠2,∠3,∠4的度数分别为________________________.
(2)若∠2是∠3的 3倍,则∠1,∠2,∠3,∠4的度数分别为________________________.
(1)若∠1+∠3= 60? ,则∠1,∠2,∠3,∠4的度数分别为________________________ .
30? 、150? 、30?、150?
45?、 135?、 45?、 135?
40?、140?、40? 、140?
巩固练习
如图所示,直线a和b相交于点O,完成下列各题:
例2 如图,直线AB、CD,EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:∵∠1=40°, ∠BOC=110°(已知),
∴∠BOF=∠BOC-∠1 =110°-40°=70°.
∵∠BOF=∠2(对顶角相等),
∴∠2=70°(等量代换).
提示:隐含条件“对顶角相等”.
探究新知
素养考点 2
利用隐含条件求角的度数
如图,直线AB、CD、EF、MN相交,若∠2=∠5,找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ EF与AB相交,∠1+∠2=180°,
∠2+∠3= 180°,
∴∠2的补角有∠1和∠3;
∵ CD与MN相交,∠5+∠8=180°,
∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8;
巩固练习
∴∠2的补角有∠1、∠3、∠6和∠8.
如图,下列各组角中,互为对顶角的是( )
A.∠1和∠2 B.∠1和∠3
C.∠2和∠4 D.∠2和∠5
A
连接中考
1.下列各图中∠1、∠2是邻补角吗?为什么?
1
2
1
2
1
2
∠1=140° ∠1=120° ∠1=130°
∠2=40° ∠2=60° ∠2=50°
(1) (2) (3)
不是
不是
是
基础巩固题
课堂检测
2.下列各图中∠1、∠2是对顶角吗?为什么?
1
2
(2)
(3)
(4)
2
1
(1)
2
1
不是
是
不是
不是
(5)
是
1
2
1
2
课堂检测
O
3.如图两堵墙围一个角?AOB,但人不能进入围墙,我们如何去测量这个角的大小呢?
C
D
?AOB=∠COD
?AOB=180°-∠AOC
(邻补角互补)
(对顶角相等)
课堂检测
方法一:
方法二:
A
B
)
)
4.找出图中∠AOE的邻补角及对顶角,若没有请画出.
A
B
C
O
D
E
)
F
解:邻补角是∠EOB和∠AOF;
对顶角是∠BOF.
课堂检测
5.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
C
A
E
D
B
F
O
解:(1)∠AOC的邻补角是∠AOD和∠COB;
∠BOE的邻补角是∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB;
∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°;
∠COB=180°-∠AOC=130°.
课堂检测
6.如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数.
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
课堂检测
如图,直线AB、CD、EF相交,若∠1 +∠5=180°,
找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵∠1= ∠3(对顶角相等),
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°,
∴∠8= ∠1.
∵∠8= ∠6(对顶角相等),
∴∠6= ∠1.
能力提升题
课堂检测
与∠1 相等的角有:∠3、∠8、∠6.
观察下列各图,寻找对顶角(不含平角)
(1)如图a,图中共有 对对顶角;
(2)如图b,图中共有 对对顶角;
(3) 如图c,图中共有 对对顶角;
(4)研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成 对对顶角;
(5) 若有10条直线相交于一点,则可形成 对对顶角.
图c
2
6
12
n(n-1)
90
拓广探索题
课堂检测
图a
A
B
C
D
O
图b
A
B
C
D
E
F
O
A
B
C
D
E
F
G
H
O
角的
名称
特 征
性 质
相 同 点
不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边.
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边.
①都是两条直线相交而成的角;
③都是成对出现的.
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对.
①有无公共边;
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
