人教版九年级数学上册 概率初步培优讲义(无答案)
文档属性
| 名称 | 人教版九年级数学上册 概率初步培优讲义(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 236.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览



文档简介
概率初步培优讲义
知识点睛:
1.随机事件
(1)必然事件:有些事件能肯定它
,如太阳东升西落。
(2)不可能事件:有些事件能肯定它
,如一个标准大气压下,水10°C结冰。
(3)随机事件:在一定条件下,
发生也可能
的事件。
2.概率的定义:在大量重复试验中,如果事件A发生的频率会在某个常数p附近,那么这个常数p就叫做事件A的概率,记作
。
3.概率的取值范围:
。
4.概率的计算方法和步骤
(1)列出所有可能发生的结果数n;
(2)列出所求事件出现的结果数m;
(3)计算所求事件发生的可能性P(所求事件)=
。
5.会用列表法、画树状图法等列举方法表示可能的结果,并求某一事件概率。
6.用频率估计概率:当试验的所有可能结果不是有限个,或各种结果发生的可能性不相等时,我们一般还要通过统计
来估计概率,当试验次数不断增大时,频率逐渐
。
例题精讲:
例题1:甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为-7,-1,3。乙袋中的三张卡片所标的数值为-2,1,6。先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标。
(1)用适当的方法写出点A(x,y)的所有情况。
(2)求点A落在第三象限的概率。
变式练习1:
在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y。
(1)计算由x、y确定的点(x,y)在函数图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜,则这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
例题2:某校将举办“心怀感恩·孝敬父母”的活动,为此,校学生会就全校1000名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图。
(1)本次调查抽取的人数为_______,估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为_______;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报。请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、乙两名同学的概率。
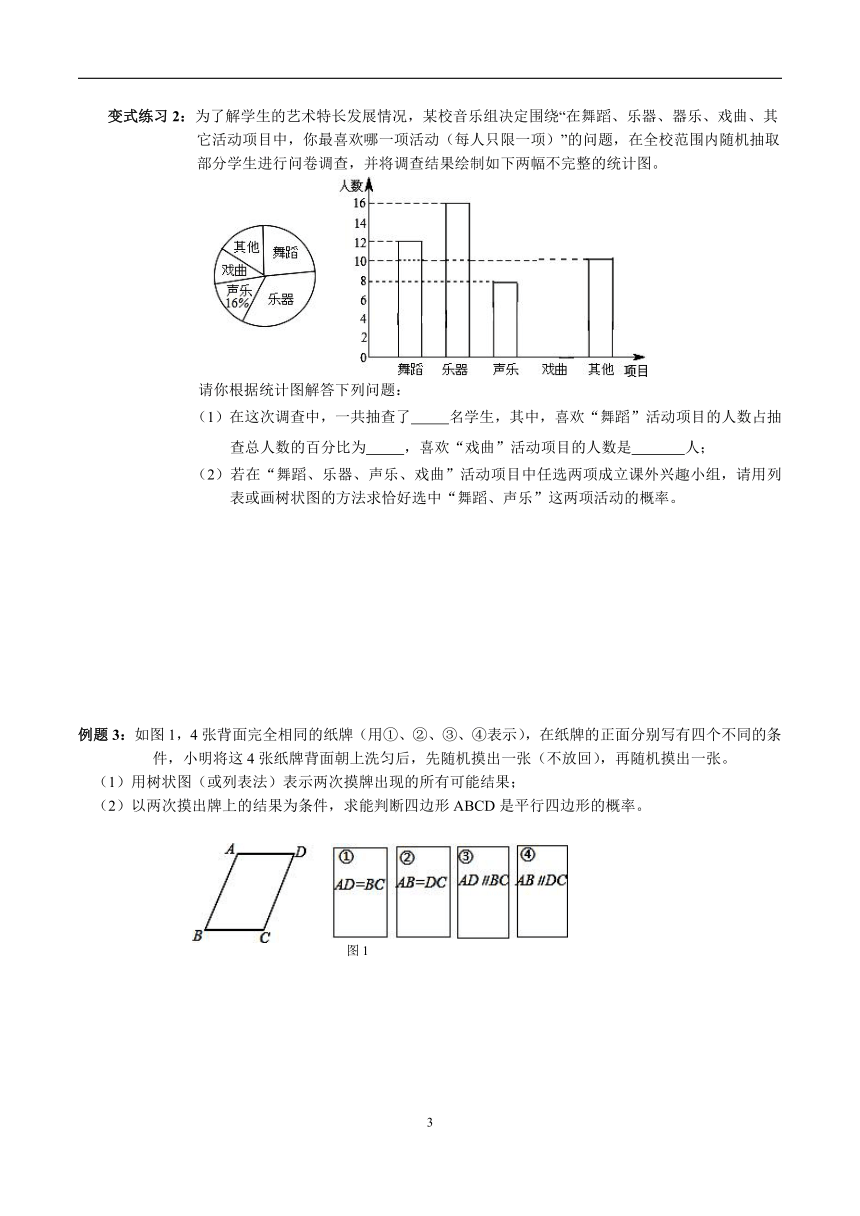
变式练习2:为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、器乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图。
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了
名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为
,喜欢“戏曲”活动项目的人数是
人;
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率。
例题3:如图1,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张。
(1)用树状图(或列表法)表示两次摸牌出现的所有可能结果;
(2)以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率。
例题4:在4张完全相同的卡片正面分别写上数字1,2,3,3,现将它们的背面朝上洗均匀。
(1)随机抽出一张卡片,求抽到数字“3”的概率;
(2)若随机抽出一张卡片记下数字后放回并洗均匀,再随机抽出一张卡片,求两次都是抽到数字“3”的概率;(要求画树状图或列表求解)
(3)如果再增加若干张写有数字“3”的同样卡片,洗均匀后,使得随机抽出一张卡片是数字“3”的概率为,问增加了多少张卡片?
变式练习4:
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球和黄球。怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验。摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中再继续。
活动结果:摸球实验活动一共做了50次,同级结果如下表:
球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算:由上述的摸球实验可推算:
盒中红球、黄球各占总球数的百分比分别是多少?盒中有红球多少个?
例题5:用列举法、列表法和树形图法求概率(解决复杂问题)
1.
小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如右图:
(1)请你完成下面表示游戏一个回合所有可能出现的结果的树状图;
(2)求一个回合能确定两人先下棋的概率.
解:
_________________________________________________
变式练习5:甲、乙、丙三名学生各自随机选择到A、B两个书店购书.
(1)求甲、乙两名学生在不同书店购书的概率;
(2)求甲、乙、丙三名学生在同一书店购书的概率.
解:(1) (2)
结果:(1)甲、乙两名学生在不同书店购书的概率是
(2)甲、乙、丙三名学生在同一书店购书的概率是
2.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别.现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球.
(1)请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况;
(2)求红球恰好被放入②号盒子的概率.
巩固练习:
1.“抛一枚均匀硬币,落地后正面朝上”这一事件是(
)。
A.必然事件
B.随机事件
C.确定事件
D.不可能事件
2.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为(
)。
A.
B.
C.
D.
3.在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形、等腰梯形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是(
)。
A.
B.
C.
D.1
4.在盒子里放有三张分别写有整式、、2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是(
)。
A.
B.
C.
D.
5.一个不透明的口袋中,装有红球6个,白球9个,黑球3个,
这些球除颜色不同外没有任何区别,从中任意摸出一个球,则摸到黑球的概率为_______。
6.在,1,2这三个数中任选2个数分别作为P点的横坐标和纵坐标,过P点画双曲线,该双曲线位于第一、三象限的概率是
。
7.从-2、-1、0、1、2这5个数中任取一个数,作为关于x的一元二次方程的k值,则所得的方程中有两个不相等的实数根的概率是
。
8.如图2,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字。现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y)。记S=x+y。
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜。你认为这个游戏公平吗?对谁有利?
课外作业:
1.下列说法正确的是(
)。
A.抛一枚硬币,正面一定朝上
B.掷一颗骰子,点数一定不大于6
C.为了解一种灯泡的使用寿命,宜采用普查的方法
D.“明天的降水概率为80%”,表示明天会有80%的地方下雨
2.把点、、、分别写在四张卡片上,随机抽取一张,该点在函数的图象上的概率是(
)。
A.
B.
C.
D.
3.把4张形状完全相同的卡片的正面分别写上数字1,2,3,4,洗匀后正面朝下放在桌子上,随机从中抽取一张卡片,记下数字后放回,再随机从中抽取一张卡片,则两次抽取的卡片上的数字之和等于5的概率是(
)。
A.
B.
C.
D.
4.如图5,有4张形状、大小、质地均相同的卡片,正面分别写有一个实数,背面完全相同。现将这4张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出卡片正面的实数是无理数的概率是(
)。
A.
B.
C.
D.1
5.在一个不透明的盒子中装有2个白球,个黄球,它们除颜色不同外,其余均相同。若从中随机摸出一个球,它是白球的概率为,则
。
6.
4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,
多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算
出的值大约是多少?
6
知识点睛:
1.随机事件
(1)必然事件:有些事件能肯定它
,如太阳东升西落。
(2)不可能事件:有些事件能肯定它
,如一个标准大气压下,水10°C结冰。
(3)随机事件:在一定条件下,
发生也可能
的事件。
2.概率的定义:在大量重复试验中,如果事件A发生的频率会在某个常数p附近,那么这个常数p就叫做事件A的概率,记作
。
3.概率的取值范围:
。
4.概率的计算方法和步骤
(1)列出所有可能发生的结果数n;
(2)列出所求事件出现的结果数m;
(3)计算所求事件发生的可能性P(所求事件)=
。
5.会用列表法、画树状图法等列举方法表示可能的结果,并求某一事件概率。
6.用频率估计概率:当试验的所有可能结果不是有限个,或各种结果发生的可能性不相等时,我们一般还要通过统计
来估计概率,当试验次数不断增大时,频率逐渐
。
例题精讲:
例题1:甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为-7,-1,3。乙袋中的三张卡片所标的数值为-2,1,6。先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标。
(1)用适当的方法写出点A(x,y)的所有情况。
(2)求点A落在第三象限的概率。
变式练习1:
在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y。
(1)计算由x、y确定的点(x,y)在函数图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜,则这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
例题2:某校将举办“心怀感恩·孝敬父母”的活动,为此,校学生会就全校1000名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图。
(1)本次调查抽取的人数为_______,估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为_______;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报。请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、乙两名同学的概率。
变式练习2:为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、器乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图。
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了
名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为
,喜欢“戏曲”活动项目的人数是
人;
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率。
例题3:如图1,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张。
(1)用树状图(或列表法)表示两次摸牌出现的所有可能结果;
(2)以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率。
例题4:在4张完全相同的卡片正面分别写上数字1,2,3,3,现将它们的背面朝上洗均匀。
(1)随机抽出一张卡片,求抽到数字“3”的概率;
(2)若随机抽出一张卡片记下数字后放回并洗均匀,再随机抽出一张卡片,求两次都是抽到数字“3”的概率;(要求画树状图或列表求解)
(3)如果再增加若干张写有数字“3”的同样卡片,洗均匀后,使得随机抽出一张卡片是数字“3”的概率为,问增加了多少张卡片?
变式练习4:
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球和黄球。怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验。摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中再继续。
活动结果:摸球实验活动一共做了50次,同级结果如下表:
球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算:由上述的摸球实验可推算:
盒中红球、黄球各占总球数的百分比分别是多少?盒中有红球多少个?
例题5:用列举法、列表法和树形图法求概率(解决复杂问题)
1.
小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如右图:
(1)请你完成下面表示游戏一个回合所有可能出现的结果的树状图;
(2)求一个回合能确定两人先下棋的概率.
解:
_________________________________________________
变式练习5:甲、乙、丙三名学生各自随机选择到A、B两个书店购书.
(1)求甲、乙两名学生在不同书店购书的概率;
(2)求甲、乙、丙三名学生在同一书店购书的概率.
解:(1) (2)
结果:(1)甲、乙两名学生在不同书店购书的概率是
(2)甲、乙、丙三名学生在同一书店购书的概率是
2.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别.现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球.
(1)请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况;
(2)求红球恰好被放入②号盒子的概率.
巩固练习:
1.“抛一枚均匀硬币,落地后正面朝上”这一事件是(
)。
A.必然事件
B.随机事件
C.确定事件
D.不可能事件
2.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为(
)。
A.
B.
C.
D.
3.在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形、等腰梯形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是(
)。
A.
B.
C.
D.1
4.在盒子里放有三张分别写有整式、、2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是(
)。
A.
B.
C.
D.
5.一个不透明的口袋中,装有红球6个,白球9个,黑球3个,
这些球除颜色不同外没有任何区别,从中任意摸出一个球,则摸到黑球的概率为_______。
6.在,1,2这三个数中任选2个数分别作为P点的横坐标和纵坐标,过P点画双曲线,该双曲线位于第一、三象限的概率是
。
7.从-2、-1、0、1、2这5个数中任取一个数,作为关于x的一元二次方程的k值,则所得的方程中有两个不相等的实数根的概率是
。
8.如图2,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字。现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y)。记S=x+y。
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜。你认为这个游戏公平吗?对谁有利?
课外作业:
1.下列说法正确的是(
)。
A.抛一枚硬币,正面一定朝上
B.掷一颗骰子,点数一定不大于6
C.为了解一种灯泡的使用寿命,宜采用普查的方法
D.“明天的降水概率为80%”,表示明天会有80%的地方下雨
2.把点、、、分别写在四张卡片上,随机抽取一张,该点在函数的图象上的概率是(
)。
A.
B.
C.
D.
3.把4张形状完全相同的卡片的正面分别写上数字1,2,3,4,洗匀后正面朝下放在桌子上,随机从中抽取一张卡片,记下数字后放回,再随机从中抽取一张卡片,则两次抽取的卡片上的数字之和等于5的概率是(
)。
A.
B.
C.
D.
4.如图5,有4张形状、大小、质地均相同的卡片,正面分别写有一个实数,背面完全相同。现将这4张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出卡片正面的实数是无理数的概率是(
)。
A.
B.
C.
D.1
5.在一个不透明的盒子中装有2个白球,个黄球,它们除颜色不同外,其余均相同。若从中随机摸出一个球,它是白球的概率为,则
。
6.
4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,
多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算
出的值大约是多少?
6
同课章节目录
