苏科版七年级数学上册第四章《一元一次方程》应用易错题专项提升训练(二)(word版含解析)
文档属性
| 名称 | 苏科版七年级数学上册第四章《一元一次方程》应用易错题专项提升训练(二)(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 89.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 19:46:57 | ||
图片预览




文档简介
第四章《一元一次方程》应用易错题专项提升训练(二)
1.如图1,在数轴上有一条线段AB,表示的数分别是﹣3和﹣9.
(1)若将线段AB的一端平移到原点处,则平移的距离为
;
(2)如图2,C为线段AB上一点,以点C为折点,将此数轴向右对折,若点B落在点A的右边且AC=BC,求C点对应的数;
(3)移动线段AB,使A对应的数为8,则B对应的数为
(直接填空),此时数轴上的动点M从A出发,以4个单位长度/秒的速度向左作匀速运动,N从B出发以2个单位长度/秒的速度向左作匀速运动,请问数轴上是否存在定点P,当动点M在线段OA(O为原点)上移动过程中始终满足OM=2PN,若存在求点P对应的数;若不存在,请说明理由.
2.如图,点C在线段AB上.点P从点C出发向点B运动,速度为2cm/s;同时,点Q也从点C出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,速度为4cm/s.最终,点Q比点P早1s到达B处.设点P运动的时间为ts.
(1)线段AC的长为
cm;当t=3s时,P,Q两点之间的距离为
cm;
(2)求线段BC的长;
(3)从P,Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P,Q两点相距1cm?
3.周末,小明和爸爸在800米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
小明:您要5分钟才能第一次追上我.
爸爸:我骑完一圈的时候,你才骑了半圈!
(Ⅰ)请根据他们的对话内容,求小明和爸爸的骑行速度(速度单位:米/秒);
(Ⅱ)爸爸第一次追上小明后,在第二次相遇前,再经过多少秒,小明和爸爸相距80米?
4.我们知道,在数轴上,表示数|a|表示的点到原点的距离,这是绝对值的几何意义,进一步地,如果数轴上两个点A、B,分别对应数a,b,那么A、B两点间的距离为:AB=|a﹣b|
如图,点A在数轴上对应的数为a,点B对应的数为b,且a,b满足:|a+3|+(b﹣2)2=0
(1)求a,b的值;
(2)求线段AB的长;
(3)如图①,点C在数轴上对应的数为x,且是方程x+1=x﹣2的解,在数轴上是否存在点M使MA+MB=BC+AB?若存在,求出点M对应的数;若不存在,说明理由.
(4)如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断NQ﹣BP的值是不变的还是变化的,如果不变请直接写出其值,如果是变化的请说明理由.
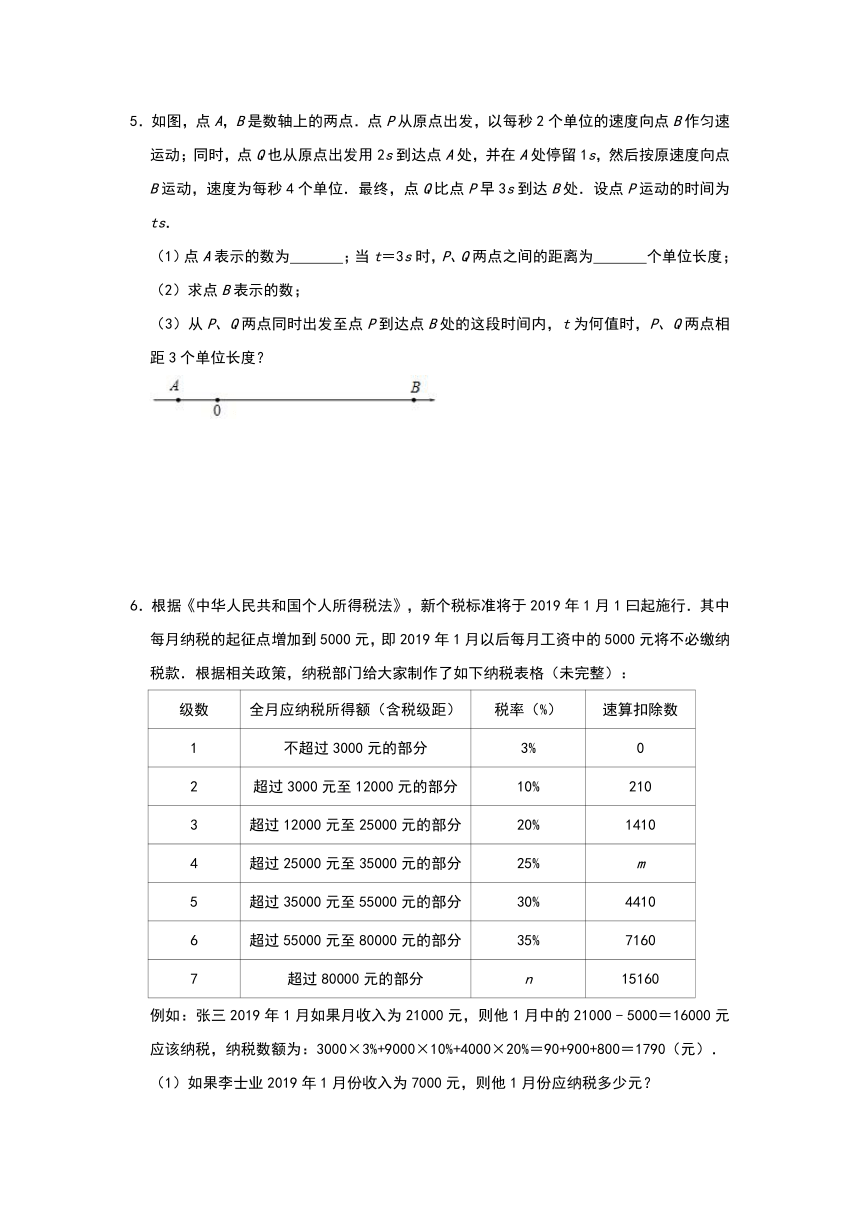
5.如图,点A,B是数轴上的两点.点P从原点出发,以每秒2个单位的速度向点B作匀速运动;同时,点Q也从原点出发用2s到达点A处,并在A处停留1s,然后按原速度向点B运动,速度为每秒4个单位.最终,点Q比点P早3s到达B处.设点P运动的时间为ts.
(1)点A表示的数为
;当t=3s时,P、Q两点之间的距离为
个单位长度;
(2)求点B表示的数;
(3)从P、Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P、Q两点相距3个单位长度?
6.根据《中华人民共和国个人所得税法》,新个税标准将于2019年1月1曰起施行.其中每月纳税的起征点増加到5000元,即2019年1月以后每月工资中的5000元将不必缴纳税款.根据相关政策,纳税部门给大家制作了如下纳税表格(未完整):
级数
全月应纳税所得额(含税级距)
税率(%)
速算扣除数
1
不超过3000元的部分
3%
0
2
超过3000元至12000元的部分
10%
210
3
超过12000元至25000元的部分
20%
1410
4
超过25000元至35000元的部分
25%
m
5
超过35000元至55000元的部分
30%
4410
6
超过55000元至80000元的部分
35%
7160
7
超过80000元的部分
n
15160
例如:张三2019年1月如果月收入为21000元,则他1月中的21000﹣5000=16000元应该纳税,纳税数额为:3000×3%+9000×10%+4000×20%=90+900+800=1790(元).
(1)如果李士业2019年1月份收入为7000元,则他1月份应纳税多少元?
(2)如果王努利2019年1月份收入为10000元,则他月份应纳税多少元?
(3)钱勒凤跟朋友说,估计自己1月份应纳税3400元,则钱勤奋1月份收入约有多少元?
(4)根据表中各数据关系,求表格中的m,n的值.
7.A、B两地相距64千米,甲从A地出发,每小时行14千米,乙从B地出发,每小时行18千米.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需几小时两人相距16千米?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10千米?
8.定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点.已知数轴上A,B两点对应数分别为a和b,(a+2)2+|b﹣4|=0,P为数轴上一动点,对应数为x.
(1)a=
,b=
;
(2)若点P为线段AB的中点,则P点对应的数x为
.若B为线段AP的中点时则P点对应的数x为
.
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从﹣16处以2个单位长度/秒向右运动.
①设运动的时间为t秒,直接用含t的式子填空
AP=
;BP=
.
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?
9.如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离.
(1)求AB的值;
(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;
(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.
10.甲,乙两人沿湖边环形道上匀速跑步,他们开启了微信运动﹣﹣微信上实时统计每天步数的软件.已知乙的步距比甲的步距少0.4m(步距是指每一步的距离),且每2分钟甲比乙多跑25步,两人各跑3周后到达同一地点,跑3圈前后的时刻和步数如下:
出发时刻
出发时微信运动中显示的步数
结束时刻
结束时微信运动中显示的步数
甲
9:30
2158
9:40
4158
乙
a
1308
9:40
4308
(1)求甲,乙的步距和环形道的周长;
(2)求表中a的值;
(3)若两人于9:40开始反向跑,问:此后,当微运动中显示的步数相差50步时,他们相遇了几次?
11.已知数轴上顺次有A、B、C三点,分别表示数a、b、c,并且满足(a+12)2+|b+5|=0,b与c互为相反数.一只电子小蜗牛从A点向正方向移动,速度为2个单位/秒.
(1)请求出A、B、C三点分别表示的数;
(2)运动多少秒时,小蜗牛到点B的距离为1个单位长度;
(3)设点P在数轴上点A的右边,且点P分别到点A、点B、点C的距离之和是20,那么点P所表示的数是
.
12.点A、B、C在数轴上表示的数分别为a,b,c,且a,b,c满足(b+2)2+(c﹣24)2=0,多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)a的值为
,b的值为
,c的值为
;
(2)若数轴上有三个动点M、N、P,分别从点A、B、C开始同时出发在数轴上运动,速度分别为每秒1个单位长度、7个单位长度3个单位长度.
①若点P向左运动,点M向右运动,点N先向左运动,遇到点M后回头再向右运动,遇到点P后又回头再向左运动,……,这样直到点P遇到点M时三点都停止运动,求点N所走的路程;
②若点M、N向右运动,点P向左运动,点Q为线段PN中点,在运动过程中,OQ﹣MN的值是否发生变化?若不变,求其值;若变化,说明理由.
13.为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60元
50元
40元
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
14.已知:数轴上点A、C对应的数分别为a、c,且满足|a+7|+(c﹣1)2018=0,点B对应的数为﹣3,
(1)求数a=
,c=
;
(2)若动点P、Q分别从A、B同时出发向右运动,点P的速度为3个单位长度/秒;点Q的速度为1个单位长度/秒,求经过多长时间P,Q两点的距离为;
(3)在(2)的条件下,若点Q运动到点C立刻原速返回,到达点B后停止运动,点P运动至点C处又以原速返回,到达点A后又折返向C运动,当点Q停止运动点P随之停止运动.求在整个运动过程中,两点P,Q同时到达的点在数轴上表示的数.
15.渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;
于是他立即原地调头追赶帽子,原地调转船头用了10分钟.
计算:
(1)求顺水速度,逆水速度是多少?
(2)从帽子丢失到发觉经过了多少时间?
(3)从发觉帽子丢失到捡回帽子经过了多少时间?
参考答案
1.解:(1)∵数轴上有一条线段AB,表示的数分别是﹣3和﹣9,
∴平移的距离为3或9;
故答案为:3或9;
(2)如图2,设点C对应的数为x,则对折后BC=x+9,
∵AC=BC,
∴﹣3﹣x=,
x=﹣4,
答:C点对应的数是﹣4;
(3)移动线段AB,使A对应的数为8,则B对应的数为2,
故答案为:2;
设点P对应的数是y,t秒时满足OM=2PN,此时点M表示的数是:8﹣4t,点N表示的数是:2﹣2t,
∵动点M在线段OA(O为原点)上移动,
∴0≤t≤2,
∵OM=2PN,
∴8﹣4t=2|y﹣2+2t|,
①8﹣4t=2(y﹣2+2t),
y=﹣4t+6,
y随t的变化而变化,不符合题意,
②8﹣4t=2(﹣y+2﹣2t),
解得:y=﹣2,
答:存在,点P对应的数是﹣2.
2.解:(1)∵点P运动的时间为ts
∴点Q运动的时间是(t﹣1)
点P从C﹣B所走的路程为:2t
∵点Q先到了A点用时1s,又在点A处停留2s
∴点Q从C﹣B所用时间是:(t﹣1﹣1﹣2﹣1)=t﹣5
∴点Q从C﹣B所走的路程为:4(t﹣5)
∴2t=4(t﹣5)
解得:t=10
∴AC=4×1=4cm
BC=10×2=20
当t=3时
点Q在点A处
而CP=2×3=6cm
∴PQ=AC+CP=4+6=10cm
(2)由(1)知:当t=10时,CB=2t=2×10=20
(3)①:当点Q在AC上时:
PQ=CP+CQ=4t+2t=1
解得:t=
②当点Q在CB上且在点P的左侧时:
PQ=CP﹣CQ=2t﹣4(t﹣4)=1
解得:t=
③当点Q在CB上且在点P的右侧时:
PQ=CQ﹣CP=4(t﹣4)﹣2t=1
解得:t=
④当点Q到达点B处时
PQ=CB﹣CP=20﹣2t=1
解得:t=
答:当P,Q两点同时出发至点P到达点B处的这段时间内,t为,,,时,P,Q两点相距1cm.
3.解:(Ⅰ)设小明的骑行速度为x米/秒,则爸爸的骑行速度为2x米/秒,根据题意得,
300×2x﹣300x=800,
解得,x=,
∴2x=.
答:小明和爸爸的骑行速度分别米/秒,米/秒.
(Ⅱ)设爸爸第一次追上小明后,在第二次相遇前,再经过z秒,小明和爸爸相距80米,根据题意得,
①当爸爸超过小明80米时,则
,
解得,z=30(秒);
②当爸爸还差80米赶上小明时,则
,
解得,z=270(秒).
答:爸爸第一次追上小明后,在第二次相遇前,再经过30秒或270秒,小明和爸爸相距80米.
4.解:(1)∵|a+3|+(b﹣2)2=0,
∴a+3=0,且b﹣2=0,
解得,a=﹣3,b=2;
(2)AB=|﹣3﹣2|=5;
(3)存在.
设M点对应的数为m,
解方程x+1=x﹣2,得x=﹣6,
∴点C对应的数为﹣6,
∵MA+MB=BC+AB,
∴|m+3|+|m﹣2|=×|﹣6﹣2|+|﹣3﹣2|,
即|m+3|+|m﹣2|=9,
①当m≤﹣3时,有﹣m﹣3+2﹣m=9,
解得,m=﹣5;
②当﹣3<m≤2时,有m+3+2﹣m=9,
此方程无解;
③当m>2时,有m+3+m﹣2=9,
解得,m=4.
综上,M点对应的数为:﹣5或4.
(4)设点N对应的数为n,则NA=n+3,NB=n﹣2,
∵若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,
∴n>2,QN=NA=n+,BP=n﹣,
∴NQ﹣BP=×(n+)﹣×(n﹣)=n+﹣n+=.
5.解:(1)∵Q从原点出发用2s到达点A处,且速度为每秒4个单位
∴|OA|=2×4=8
又∵A点在原点的左侧
∴A:﹣8
当t=3s时
又∵Q也从原点出发用2s到达点A处,并在A处停留1s
∴|OQ|=|OA|=8
∵点P从原点出发,以每秒2个单位的速度向点B作匀速运动
∴|OP|=2×3=6
∴|PQ|=|OQ|+|OP|=6+8=14
(2):点P从原点运动到点B的时间为t,
∴8+2t=4(t﹣6)
解得:t=16
∴BC=2t=32
∴点B表示的数是32
(3):由(2)得:∵点P到达点B处需要16s,点Q到达点B处需要13s,
∴P、Q两点相距3个单位长度分四种情况:
①:当点Q从O﹣﹣A上时,4t+2t=3,解得:t=
②:当点Q从O﹣﹣A﹣﹣B上时且在P的左侧时,8+2t=4(t﹣3)+3,解得:t=
③:当点Q从O﹣﹣A﹣﹣B上时且在P的右侧时,8+2t+3=4(t﹣3),解得:t=
④:当点Q到达点B时:2t+3=32,解得:t=
∵t<16s
∴当P、Q两点相距3个单位长度,t的值为:,,,.
6.解:(1)∵(7000﹣5000)×3%=60元;
∴1月份纳税60元;
(2)∵3000×3%+(10000﹣5000﹣3000)×10%=290元,
∴应纳税290元;
(3)设1月份收入为x元,依题意得,
3000×3%+9000×10%+(x﹣5000﹣3000﹣9000)×20%=3400
解得,x=29050.
∴1月收入约有29050元.
(4)由数据关系可知,m=3000×22%+9000×15%+13000×5%=2660;
依题意得,80000×(n﹣35%)+7160=15160
解得,n=45%.
故答案为m=2660;n=45%.
7.解:(1)设两人同时出发相向而行,需经过x小时两人相遇,
根据题意得:14x+18x=64,
解方程得:x=2(小时).
答:两人同时出发相向而行,需经过2小时两人相遇;
(2)设两人同时出发相向而行,需y小时两人相距16千米,
①当两人没有相遇他们相距16千米,
根据题意得:14y+18y+16=64,
解方程得:y=1.5(小时);
②当两人已经相遇他们相距16千米,
依题意得14y+18y=64+16,
∴y=2.5(小时).
答:若两人同时出发相向而行,则需1.5或2.5小时两人相距16千米;
(3)设甲在前,乙在后,两人同时同向而行,则z小时后乙超过甲10千米,
根据题意得:18z=14z+64+10,
解方程得:z=18.5(小时).
答:若甲在前,乙在后,两人同时同向而行,则18.5小时后乙超过甲10千米.
8.解:(1)因为(a+2)2+|b﹣4|=0,
所以a=﹣2,b=4.
故答案为﹣2、4
(2)若点P为线段AB的中点,则P点对应的数x为1.
若B为线段AP的中点时,AB=BP=6,则P点对应的数x为10.
故答案为1、10.
(3)①AP=﹣3t+14或3t﹣14或|14﹣3t|,
BP=20﹣3t或3t﹣20或|20﹣3t|.
故答案为﹣3t+14或3t﹣14或|14﹣3t|、20﹣3t或3t﹣20或|20﹣3t|.
②ts后,点A的位置为:﹣2﹣t,点B的位置为:4﹣t,点P的位置为:﹣16+2t,
当点A是PB的中点时,则﹣2﹣t﹣(﹣16+2t)=6
解得:t=,
当点P是AB的中点时,则﹣16+2t﹣(﹣2﹣t)=3
解得:t=,
当点B是PA的中点时,则﹣16+2t﹣(4﹣t)=6
解得:t=.
答:经过s、s、s后,点A、点B、点P三点中其中一点是另外两点的中点.
9.解:(1)∵数轴上两点A,B表示的数分别为﹣2,6
∴AB=6﹣(﹣2)=8
答:AB的值为8.
(2)设点C表示的数为x,由题意得
|x﹣(﹣2)|=3|x﹣6|
∴|x+2|=3|x﹣6|
∴x+2=3x﹣18或x+2=18﹣3x
∴x=10或x=4
答:点C表示的数为4或10.
(3)∵点C位于A,B两点之间,
∴点C表示的数为4,点A运动t秒后所表示的数为﹣2+t,
①点C到达B之前,即2<t<3时,点C表示的数为4+2(t﹣2)=2t
∴AC=t+2,BC=6﹣2t
∴t+2=3(6﹣2t)
解得t=
②点C到达B之后,即t>3时,点C表示的数为6﹣2(t﹣3)=12﹣2t
∴AC=|﹣2+t﹣(12﹣2t)|=|3t﹣14|,BC=6﹣(12﹣2t)=2t﹣6
∴|3t﹣14|=3(2t﹣6)
解得t=或t=,其中<3不符合题意舍去
答:t的值为和
10.(1)设乙的步距为xm,由于乙的步距比甲的步距少0.4m,则甲的步距少为(x+0.4)m,根据表格列方程得:
(4158﹣2158)(x+0.4)=(4308﹣1308)x,
∴2000x+800=3000x,
∴x=0.8,0.8+0.4=1.2,
∴环形道的周长为:3000×0.8÷3=800m.
故甲的步距为1.2m,乙的步距为0.8m,环形道的周长为800m.
(2)由表格知,甲10分钟跑了2000步,则甲每分钟跑200步,每2分钟跑400步,
∵每2分钟甲比乙多跑25步,
∴每2分钟乙跑375步,
∴3000÷375=8,2×8=16分钟,
∴a为9:24.
故答案为:9:24.
(3)每2分钟甲比乙多跑25步,9:40时,两人在微信运动显示的步数有150步的差数,因此反向跑当微运动中显示的步数相差50步时,实际上甲应该比乙多跑了100步或200步,
当甲比乙多跑了100步时,2×(100÷25)=8分钟,
甲每分钟跑200步,甲的步距为1.2m,每2分钟乙跑375步,乙的步距为0.8m,
(200×1.2×8+0.8×375×4)÷800=3.9,则甲乙相遇了3次;
当甲比乙多跑了200步时,2×(200÷25)=16分钟,
(200×1.2×16+0.8×375×8)÷800=7.8,此时甲乙相遇了7次.
∴反向跑当微运动中显示的步数相差50步时,他们相遇了3次或7次.
11.解:(1)∵(a+12)2+|b+5|=0,
∴a+12=0,b+5=0,
解得:a=﹣12,b=﹣5,
又∵b与c互为相反数,
∴b+c=0,
∴c=5;
(2)若小蜗牛运动到B前相距1个单位长度时,
运动时间为x秒,
∵AB的距离为|﹣12﹣(﹣5)|=7,
∴2x+1=7,
解得:x=3;
若小蜗牛运动到B后相距1个单位长度时,
运动时间为y秒,依题意得:
2y=7+1,
解得:y=4,
综合所述:经过3秒或4秒时,小蜗牛到点B的距离为1个单位长度;
(3)设点P表示数为z,
∵AC的距离为|﹣12﹣5|=17,
BC的距离为|5﹣(﹣5)|=10,
∴点P只能在AC之间,不可能在点C的右边;
又∵PA+PC=17,PA+PB+PC=20,
∴|PB|=3
∴|z﹣(﹣5)|=3,
解得:z=﹣8或z=﹣2.
12.解:(1)∵(b+2)2+(c﹣24)2=0,
∴b=﹣2,c=24,
∵多项式x|a+3|y2一ax3y+xy2﹣1是五次四项式,
∴|a+3|=5﹣2,﹣a≠0,
∴a=﹣6;
故答案是:﹣6,﹣2,24;
(2)①点P,M相遇时间t==7.5,
∴N点所走路程:7.5×7=52.5(单位长度);
②OQ﹣MN的值不发生变化;理由如下:
设运动的时间为t秒,
则MN=(7﹣1)t+4=6t+4,
∵动点M、N、P,分别从点A、B、C开始同时出发在数轴上运动,B、C在数轴上表示的数分别为﹣2,24,
∴运动t秒时点N、P分别位于数轴上﹣2+7t、24﹣3t的位置,
∴PN中点Q位于:(﹣2+7t+24﹣3t)÷2=11+2t,
∴OQ=11+2t,
∴OQ﹣MN=11+2t﹣(6t+4)=11+2t﹣2t﹣=,
∴在运动过程中,OQ﹣MN的值不发生变化.
13.解:(1)设甲校x人,则乙校(92﹣x)人,依题意得
50x+60(92﹣x)=5000,
x=52,
∴92﹣x=40,
答:甲校有52人参加演出,乙校有40人参加演出.
(2)乙:92﹣52=40人,
甲:52﹣10=42人,
两校联合:50×(40+42)=4100元,
而此时比各自购买节约了:(42×60+40×60)﹣4100=820元
若两校联合购买了91套只需:40×91=3640元,
此时又比联合购买节约:4100﹣3640=460元
因此,最省钱的购买方案是两校联合购买91套服装,
即比实际人数多买91﹣(40+42)=9套.
14.解:(1)由非负数的性质可得:,
∴a=﹣7,c=1,
故答案为:﹣7,1.
(2)设经过t秒两点的距离为,
由题意得:|1×t+4﹣3t|=,
解得t=或,
答:经过秒或秒P,Q两点的距离为.
(3)点P未运动到点C时,设经过x秒P,Q相遇,
由题意得:3x=x+4,
∴x=2,
表示的数为:﹣7+3×2=﹣1,
点P运动到点C返回时,设经过y秒P,Q相遇,
由题意得:3y+y+4=2[1﹣(﹣7)],
∴y=3,
表示的数是:3×3﹣[1﹣(﹣7)]﹣1=0,
当点P返回到点A时,用时秒,此时点Q所在位置表示的数是﹣,
设再经过z秒相遇,
由题意得:3z+z=﹣﹣(﹣7),
∴z=,
表示的数是:﹣7+×3=﹣2,
答:在整个运动过程中,两点P,Q同时到达的点在数轴上表示的数分别是﹣1,0,﹣2.
15.解:(1)∵顺水速度=静水速度+水流速度,
逆水速度=静水速度﹣水流速度,
∴顺水速度是5+3=8,逆水速度是5﹣3=2.
答:顺水速度是每小时8里,逆水速度是每小时2里.
(2)设从帽子丢失到发觉经过了x小时.
根据题意,得
5x=2.5,解得x=0.5.
答:从帽子丢失到发觉经过了0.5小时.
(3)设原地调转船头后到捡回帽子经过了y小时,
则从发觉帽子丢失到捡回帽子经过(y+)小时.
根据题意,得
方程应为8y=2.5+3×(y+)
解得y=.∴y+=
答:从发觉帽子丢失到捡回帽子经过小时.
1.如图1,在数轴上有一条线段AB,表示的数分别是﹣3和﹣9.
(1)若将线段AB的一端平移到原点处,则平移的距离为
;
(2)如图2,C为线段AB上一点,以点C为折点,将此数轴向右对折,若点B落在点A的右边且AC=BC,求C点对应的数;
(3)移动线段AB,使A对应的数为8,则B对应的数为
(直接填空),此时数轴上的动点M从A出发,以4个单位长度/秒的速度向左作匀速运动,N从B出发以2个单位长度/秒的速度向左作匀速运动,请问数轴上是否存在定点P,当动点M在线段OA(O为原点)上移动过程中始终满足OM=2PN,若存在求点P对应的数;若不存在,请说明理由.
2.如图,点C在线段AB上.点P从点C出发向点B运动,速度为2cm/s;同时,点Q也从点C出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,速度为4cm/s.最终,点Q比点P早1s到达B处.设点P运动的时间为ts.
(1)线段AC的长为
cm;当t=3s时,P,Q两点之间的距离为
cm;
(2)求线段BC的长;
(3)从P,Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P,Q两点相距1cm?
3.周末,小明和爸爸在800米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:
小明:您要5分钟才能第一次追上我.
爸爸:我骑完一圈的时候,你才骑了半圈!
(Ⅰ)请根据他们的对话内容,求小明和爸爸的骑行速度(速度单位:米/秒);
(Ⅱ)爸爸第一次追上小明后,在第二次相遇前,再经过多少秒,小明和爸爸相距80米?
4.我们知道,在数轴上,表示数|a|表示的点到原点的距离,这是绝对值的几何意义,进一步地,如果数轴上两个点A、B,分别对应数a,b,那么A、B两点间的距离为:AB=|a﹣b|
如图,点A在数轴上对应的数为a,点B对应的数为b,且a,b满足:|a+3|+(b﹣2)2=0
(1)求a,b的值;
(2)求线段AB的长;
(3)如图①,点C在数轴上对应的数为x,且是方程x+1=x﹣2的解,在数轴上是否存在点M使MA+MB=BC+AB?若存在,求出点M对应的数;若不存在,说明理由.
(4)如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断NQ﹣BP的值是不变的还是变化的,如果不变请直接写出其值,如果是变化的请说明理由.
5.如图,点A,B是数轴上的两点.点P从原点出发,以每秒2个单位的速度向点B作匀速运动;同时,点Q也从原点出发用2s到达点A处,并在A处停留1s,然后按原速度向点B运动,速度为每秒4个单位.最终,点Q比点P早3s到达B处.设点P运动的时间为ts.
(1)点A表示的数为
;当t=3s时,P、Q两点之间的距离为
个单位长度;
(2)求点B表示的数;
(3)从P、Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P、Q两点相距3个单位长度?
6.根据《中华人民共和国个人所得税法》,新个税标准将于2019年1月1曰起施行.其中每月纳税的起征点増加到5000元,即2019年1月以后每月工资中的5000元将不必缴纳税款.根据相关政策,纳税部门给大家制作了如下纳税表格(未完整):
级数
全月应纳税所得额(含税级距)
税率(%)
速算扣除数
1
不超过3000元的部分
3%
0
2
超过3000元至12000元的部分
10%
210
3
超过12000元至25000元的部分
20%
1410
4
超过25000元至35000元的部分
25%
m
5
超过35000元至55000元的部分
30%
4410
6
超过55000元至80000元的部分
35%
7160
7
超过80000元的部分
n
15160
例如:张三2019年1月如果月收入为21000元,则他1月中的21000﹣5000=16000元应该纳税,纳税数额为:3000×3%+9000×10%+4000×20%=90+900+800=1790(元).
(1)如果李士业2019年1月份收入为7000元,则他1月份应纳税多少元?
(2)如果王努利2019年1月份收入为10000元,则他月份应纳税多少元?
(3)钱勒凤跟朋友说,估计自己1月份应纳税3400元,则钱勤奋1月份收入约有多少元?
(4)根据表中各数据关系,求表格中的m,n的值.
7.A、B两地相距64千米,甲从A地出发,每小时行14千米,乙从B地出发,每小时行18千米.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需几小时两人相距16千米?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10千米?
8.定义:若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点.已知数轴上A,B两点对应数分别为a和b,(a+2)2+|b﹣4|=0,P为数轴上一动点,对应数为x.
(1)a=
,b=
;
(2)若点P为线段AB的中点,则P点对应的数x为
.若B为线段AP的中点时则P点对应的数x为
.
(3)若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从﹣16处以2个单位长度/秒向右运动.
①设运动的时间为t秒,直接用含t的式子填空
AP=
;BP=
.
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?
9.如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离.
(1)求AB的值;
(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;
(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.
10.甲,乙两人沿湖边环形道上匀速跑步,他们开启了微信运动﹣﹣微信上实时统计每天步数的软件.已知乙的步距比甲的步距少0.4m(步距是指每一步的距离),且每2分钟甲比乙多跑25步,两人各跑3周后到达同一地点,跑3圈前后的时刻和步数如下:
出发时刻
出发时微信运动中显示的步数
结束时刻
结束时微信运动中显示的步数
甲
9:30
2158
9:40
4158
乙
a
1308
9:40
4308
(1)求甲,乙的步距和环形道的周长;
(2)求表中a的值;
(3)若两人于9:40开始反向跑,问:此后,当微运动中显示的步数相差50步时,他们相遇了几次?
11.已知数轴上顺次有A、B、C三点,分别表示数a、b、c,并且满足(a+12)2+|b+5|=0,b与c互为相反数.一只电子小蜗牛从A点向正方向移动,速度为2个单位/秒.
(1)请求出A、B、C三点分别表示的数;
(2)运动多少秒时,小蜗牛到点B的距离为1个单位长度;
(3)设点P在数轴上点A的右边,且点P分别到点A、点B、点C的距离之和是20,那么点P所表示的数是
.
12.点A、B、C在数轴上表示的数分别为a,b,c,且a,b,c满足(b+2)2+(c﹣24)2=0,多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)a的值为
,b的值为
,c的值为
;
(2)若数轴上有三个动点M、N、P,分别从点A、B、C开始同时出发在数轴上运动,速度分别为每秒1个单位长度、7个单位长度3个单位长度.
①若点P向左运动,点M向右运动,点N先向左运动,遇到点M后回头再向右运动,遇到点P后又回头再向左运动,……,这样直到点P遇到点M时三点都停止运动,求点N所走的路程;
②若点M、N向右运动,点P向左运动,点Q为线段PN中点,在运动过程中,OQ﹣MN的值是否发生变化?若不变,求其值;若变化,说明理由.
13.为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60元
50元
40元
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
14.已知:数轴上点A、C对应的数分别为a、c,且满足|a+7|+(c﹣1)2018=0,点B对应的数为﹣3,
(1)求数a=
,c=
;
(2)若动点P、Q分别从A、B同时出发向右运动,点P的速度为3个单位长度/秒;点Q的速度为1个单位长度/秒,求经过多长时间P,Q两点的距离为;
(3)在(2)的条件下,若点Q运动到点C立刻原速返回,到达点B后停止运动,点P运动至点C处又以原速返回,到达点A后又折返向C运动,当点Q停止运动点P随之停止运动.求在整个运动过程中,两点P,Q同时到达的点在数轴上表示的数.
15.渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;
于是他立即原地调头追赶帽子,原地调转船头用了10分钟.
计算:
(1)求顺水速度,逆水速度是多少?
(2)从帽子丢失到发觉经过了多少时间?
(3)从发觉帽子丢失到捡回帽子经过了多少时间?
参考答案
1.解:(1)∵数轴上有一条线段AB,表示的数分别是﹣3和﹣9,
∴平移的距离为3或9;
故答案为:3或9;
(2)如图2,设点C对应的数为x,则对折后BC=x+9,
∵AC=BC,
∴﹣3﹣x=,
x=﹣4,
答:C点对应的数是﹣4;
(3)移动线段AB,使A对应的数为8,则B对应的数为2,
故答案为:2;
设点P对应的数是y,t秒时满足OM=2PN,此时点M表示的数是:8﹣4t,点N表示的数是:2﹣2t,
∵动点M在线段OA(O为原点)上移动,
∴0≤t≤2,
∵OM=2PN,
∴8﹣4t=2|y﹣2+2t|,
①8﹣4t=2(y﹣2+2t),
y=﹣4t+6,
y随t的变化而变化,不符合题意,
②8﹣4t=2(﹣y+2﹣2t),
解得:y=﹣2,
答:存在,点P对应的数是﹣2.
2.解:(1)∵点P运动的时间为ts
∴点Q运动的时间是(t﹣1)
点P从C﹣B所走的路程为:2t
∵点Q先到了A点用时1s,又在点A处停留2s
∴点Q从C﹣B所用时间是:(t﹣1﹣1﹣2﹣1)=t﹣5
∴点Q从C﹣B所走的路程为:4(t﹣5)
∴2t=4(t﹣5)
解得:t=10
∴AC=4×1=4cm
BC=10×2=20
当t=3时
点Q在点A处
而CP=2×3=6cm
∴PQ=AC+CP=4+6=10cm
(2)由(1)知:当t=10时,CB=2t=2×10=20
(3)①:当点Q在AC上时:
PQ=CP+CQ=4t+2t=1
解得:t=
②当点Q在CB上且在点P的左侧时:
PQ=CP﹣CQ=2t﹣4(t﹣4)=1
解得:t=
③当点Q在CB上且在点P的右侧时:
PQ=CQ﹣CP=4(t﹣4)﹣2t=1
解得:t=
④当点Q到达点B处时
PQ=CB﹣CP=20﹣2t=1
解得:t=
答:当P,Q两点同时出发至点P到达点B处的这段时间内,t为,,,时,P,Q两点相距1cm.
3.解:(Ⅰ)设小明的骑行速度为x米/秒,则爸爸的骑行速度为2x米/秒,根据题意得,
300×2x﹣300x=800,
解得,x=,
∴2x=.
答:小明和爸爸的骑行速度分别米/秒,米/秒.
(Ⅱ)设爸爸第一次追上小明后,在第二次相遇前,再经过z秒,小明和爸爸相距80米,根据题意得,
①当爸爸超过小明80米时,则
,
解得,z=30(秒);
②当爸爸还差80米赶上小明时,则
,
解得,z=270(秒).
答:爸爸第一次追上小明后,在第二次相遇前,再经过30秒或270秒,小明和爸爸相距80米.
4.解:(1)∵|a+3|+(b﹣2)2=0,
∴a+3=0,且b﹣2=0,
解得,a=﹣3,b=2;
(2)AB=|﹣3﹣2|=5;
(3)存在.
设M点对应的数为m,
解方程x+1=x﹣2,得x=﹣6,
∴点C对应的数为﹣6,
∵MA+MB=BC+AB,
∴|m+3|+|m﹣2|=×|﹣6﹣2|+|﹣3﹣2|,
即|m+3|+|m﹣2|=9,
①当m≤﹣3时,有﹣m﹣3+2﹣m=9,
解得,m=﹣5;
②当﹣3<m≤2时,有m+3+2﹣m=9,
此方程无解;
③当m>2时,有m+3+m﹣2=9,
解得,m=4.
综上,M点对应的数为:﹣5或4.
(4)设点N对应的数为n,则NA=n+3,NB=n﹣2,
∵若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,
∴n>2,QN=NA=n+,BP=n﹣,
∴NQ﹣BP=×(n+)﹣×(n﹣)=n+﹣n+=.
5.解:(1)∵Q从原点出发用2s到达点A处,且速度为每秒4个单位
∴|OA|=2×4=8
又∵A点在原点的左侧
∴A:﹣8
当t=3s时
又∵Q也从原点出发用2s到达点A处,并在A处停留1s
∴|OQ|=|OA|=8
∵点P从原点出发,以每秒2个单位的速度向点B作匀速运动
∴|OP|=2×3=6
∴|PQ|=|OQ|+|OP|=6+8=14
(2):点P从原点运动到点B的时间为t,
∴8+2t=4(t﹣6)
解得:t=16
∴BC=2t=32
∴点B表示的数是32
(3):由(2)得:∵点P到达点B处需要16s,点Q到达点B处需要13s,
∴P、Q两点相距3个单位长度分四种情况:
①:当点Q从O﹣﹣A上时,4t+2t=3,解得:t=
②:当点Q从O﹣﹣A﹣﹣B上时且在P的左侧时,8+2t=4(t﹣3)+3,解得:t=
③:当点Q从O﹣﹣A﹣﹣B上时且在P的右侧时,8+2t+3=4(t﹣3),解得:t=
④:当点Q到达点B时:2t+3=32,解得:t=
∵t<16s
∴当P、Q两点相距3个单位长度,t的值为:,,,.
6.解:(1)∵(7000﹣5000)×3%=60元;
∴1月份纳税60元;
(2)∵3000×3%+(10000﹣5000﹣3000)×10%=290元,
∴应纳税290元;
(3)设1月份收入为x元,依题意得,
3000×3%+9000×10%+(x﹣5000﹣3000﹣9000)×20%=3400
解得,x=29050.
∴1月收入约有29050元.
(4)由数据关系可知,m=3000×22%+9000×15%+13000×5%=2660;
依题意得,80000×(n﹣35%)+7160=15160
解得,n=45%.
故答案为m=2660;n=45%.
7.解:(1)设两人同时出发相向而行,需经过x小时两人相遇,
根据题意得:14x+18x=64,
解方程得:x=2(小时).
答:两人同时出发相向而行,需经过2小时两人相遇;
(2)设两人同时出发相向而行,需y小时两人相距16千米,
①当两人没有相遇他们相距16千米,
根据题意得:14y+18y+16=64,
解方程得:y=1.5(小时);
②当两人已经相遇他们相距16千米,
依题意得14y+18y=64+16,
∴y=2.5(小时).
答:若两人同时出发相向而行,则需1.5或2.5小时两人相距16千米;
(3)设甲在前,乙在后,两人同时同向而行,则z小时后乙超过甲10千米,
根据题意得:18z=14z+64+10,
解方程得:z=18.5(小时).
答:若甲在前,乙在后,两人同时同向而行,则18.5小时后乙超过甲10千米.
8.解:(1)因为(a+2)2+|b﹣4|=0,
所以a=﹣2,b=4.
故答案为﹣2、4
(2)若点P为线段AB的中点,则P点对应的数x为1.
若B为线段AP的中点时,AB=BP=6,则P点对应的数x为10.
故答案为1、10.
(3)①AP=﹣3t+14或3t﹣14或|14﹣3t|,
BP=20﹣3t或3t﹣20或|20﹣3t|.
故答案为﹣3t+14或3t﹣14或|14﹣3t|、20﹣3t或3t﹣20或|20﹣3t|.
②ts后,点A的位置为:﹣2﹣t,点B的位置为:4﹣t,点P的位置为:﹣16+2t,
当点A是PB的中点时,则﹣2﹣t﹣(﹣16+2t)=6
解得:t=,
当点P是AB的中点时,则﹣16+2t﹣(﹣2﹣t)=3
解得:t=,
当点B是PA的中点时,则﹣16+2t﹣(4﹣t)=6
解得:t=.
答:经过s、s、s后,点A、点B、点P三点中其中一点是另外两点的中点.
9.解:(1)∵数轴上两点A,B表示的数分别为﹣2,6
∴AB=6﹣(﹣2)=8
答:AB的值为8.
(2)设点C表示的数为x,由题意得
|x﹣(﹣2)|=3|x﹣6|
∴|x+2|=3|x﹣6|
∴x+2=3x﹣18或x+2=18﹣3x
∴x=10或x=4
答:点C表示的数为4或10.
(3)∵点C位于A,B两点之间,
∴点C表示的数为4,点A运动t秒后所表示的数为﹣2+t,
①点C到达B之前,即2<t<3时,点C表示的数为4+2(t﹣2)=2t
∴AC=t+2,BC=6﹣2t
∴t+2=3(6﹣2t)
解得t=
②点C到达B之后,即t>3时,点C表示的数为6﹣2(t﹣3)=12﹣2t
∴AC=|﹣2+t﹣(12﹣2t)|=|3t﹣14|,BC=6﹣(12﹣2t)=2t﹣6
∴|3t﹣14|=3(2t﹣6)
解得t=或t=,其中<3不符合题意舍去
答:t的值为和
10.(1)设乙的步距为xm,由于乙的步距比甲的步距少0.4m,则甲的步距少为(x+0.4)m,根据表格列方程得:
(4158﹣2158)(x+0.4)=(4308﹣1308)x,
∴2000x+800=3000x,
∴x=0.8,0.8+0.4=1.2,
∴环形道的周长为:3000×0.8÷3=800m.
故甲的步距为1.2m,乙的步距为0.8m,环形道的周长为800m.
(2)由表格知,甲10分钟跑了2000步,则甲每分钟跑200步,每2分钟跑400步,
∵每2分钟甲比乙多跑25步,
∴每2分钟乙跑375步,
∴3000÷375=8,2×8=16分钟,
∴a为9:24.
故答案为:9:24.
(3)每2分钟甲比乙多跑25步,9:40时,两人在微信运动显示的步数有150步的差数,因此反向跑当微运动中显示的步数相差50步时,实际上甲应该比乙多跑了100步或200步,
当甲比乙多跑了100步时,2×(100÷25)=8分钟,
甲每分钟跑200步,甲的步距为1.2m,每2分钟乙跑375步,乙的步距为0.8m,
(200×1.2×8+0.8×375×4)÷800=3.9,则甲乙相遇了3次;
当甲比乙多跑了200步时,2×(200÷25)=16分钟,
(200×1.2×16+0.8×375×8)÷800=7.8,此时甲乙相遇了7次.
∴反向跑当微运动中显示的步数相差50步时,他们相遇了3次或7次.
11.解:(1)∵(a+12)2+|b+5|=0,
∴a+12=0,b+5=0,
解得:a=﹣12,b=﹣5,
又∵b与c互为相反数,
∴b+c=0,
∴c=5;
(2)若小蜗牛运动到B前相距1个单位长度时,
运动时间为x秒,
∵AB的距离为|﹣12﹣(﹣5)|=7,
∴2x+1=7,
解得:x=3;
若小蜗牛运动到B后相距1个单位长度时,
运动时间为y秒,依题意得:
2y=7+1,
解得:y=4,
综合所述:经过3秒或4秒时,小蜗牛到点B的距离为1个单位长度;
(3)设点P表示数为z,
∵AC的距离为|﹣12﹣5|=17,
BC的距离为|5﹣(﹣5)|=10,
∴点P只能在AC之间,不可能在点C的右边;
又∵PA+PC=17,PA+PB+PC=20,
∴|PB|=3
∴|z﹣(﹣5)|=3,
解得:z=﹣8或z=﹣2.
12.解:(1)∵(b+2)2+(c﹣24)2=0,
∴b=﹣2,c=24,
∵多项式x|a+3|y2一ax3y+xy2﹣1是五次四项式,
∴|a+3|=5﹣2,﹣a≠0,
∴a=﹣6;
故答案是:﹣6,﹣2,24;
(2)①点P,M相遇时间t==7.5,
∴N点所走路程:7.5×7=52.5(单位长度);
②OQ﹣MN的值不发生变化;理由如下:
设运动的时间为t秒,
则MN=(7﹣1)t+4=6t+4,
∵动点M、N、P,分别从点A、B、C开始同时出发在数轴上运动,B、C在数轴上表示的数分别为﹣2,24,
∴运动t秒时点N、P分别位于数轴上﹣2+7t、24﹣3t的位置,
∴PN中点Q位于:(﹣2+7t+24﹣3t)÷2=11+2t,
∴OQ=11+2t,
∴OQ﹣MN=11+2t﹣(6t+4)=11+2t﹣2t﹣=,
∴在运动过程中,OQ﹣MN的值不发生变化.
13.解:(1)设甲校x人,则乙校(92﹣x)人,依题意得
50x+60(92﹣x)=5000,
x=52,
∴92﹣x=40,
答:甲校有52人参加演出,乙校有40人参加演出.
(2)乙:92﹣52=40人,
甲:52﹣10=42人,
两校联合:50×(40+42)=4100元,
而此时比各自购买节约了:(42×60+40×60)﹣4100=820元
若两校联合购买了91套只需:40×91=3640元,
此时又比联合购买节约:4100﹣3640=460元
因此,最省钱的购买方案是两校联合购买91套服装,
即比实际人数多买91﹣(40+42)=9套.
14.解:(1)由非负数的性质可得:,
∴a=﹣7,c=1,
故答案为:﹣7,1.
(2)设经过t秒两点的距离为,
由题意得:|1×t+4﹣3t|=,
解得t=或,
答:经过秒或秒P,Q两点的距离为.
(3)点P未运动到点C时,设经过x秒P,Q相遇,
由题意得:3x=x+4,
∴x=2,
表示的数为:﹣7+3×2=﹣1,
点P运动到点C返回时,设经过y秒P,Q相遇,
由题意得:3y+y+4=2[1﹣(﹣7)],
∴y=3,
表示的数是:3×3﹣[1﹣(﹣7)]﹣1=0,
当点P返回到点A时,用时秒,此时点Q所在位置表示的数是﹣,
设再经过z秒相遇,
由题意得:3z+z=﹣﹣(﹣7),
∴z=,
表示的数是:﹣7+×3=﹣2,
答:在整个运动过程中,两点P,Q同时到达的点在数轴上表示的数分别是﹣1,0,﹣2.
15.解:(1)∵顺水速度=静水速度+水流速度,
逆水速度=静水速度﹣水流速度,
∴顺水速度是5+3=8,逆水速度是5﹣3=2.
答:顺水速度是每小时8里,逆水速度是每小时2里.
(2)设从帽子丢失到发觉经过了x小时.
根据题意,得
5x=2.5,解得x=0.5.
答:从帽子丢失到发觉经过了0.5小时.
(3)设原地调转船头后到捡回帽子经过了y小时,
则从发觉帽子丢失到捡回帽子经过(y+)小时.
根据题意,得
方程应为8y=2.5+3×(y+)
解得y=.∴y+=
答:从发觉帽子丢失到捡回帽子经过小时.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
