苏科版数学八年级上册 6.1 函数 课件(共23张ppt)
文档属性
| 名称 | 苏科版数学八年级上册 6.1 函数 课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 828.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 18:10:53 | ||
图片预览







文档简介
(共23张PPT)
6.1 函数(1)
八年级(上册)
初中数学
探究
列车从甲地驶往乙地,在16:17到16:22这个时段,列车在匀速行驶的过程中,哪些量没有变化?哪些量不断变化的?
在这一过程中,没有变化的量是:
列车匀速行驶的速度的数值不变;
从甲地到乙地的路程的数值不变.
在这一过程中,变化了的量是:
列车行驶的时间在不断变化;
列车距离起点和终点的路程也在不断变化.
探究
常量:
在某一变化过程中,数值保持不变的量叫做常量.
变量:
在某一变化过程中,可以取不同数值的量叫做变量.
探究
你还能举出生活中的某些变化过程,并说明其中的常量和变量吗?
展示
请你用有关字母的代数式表示y,并指出其中的常量和变量.
展示
(1)n边形的内角和为y=
.
(2)以30千米/时匀速运动的汽车在t小时行驶的
路程y=
.
(3)圆的半径为r,那么圆的周长y=
.
(4)已知等腰△ABC周长为10cm,
若腰长AB为xcm,
则底边BC长为y
=
.
(n-2)·180°
30t
2πr
5-x
活动一
一石激起千层浪,水滴泛起层层波.变化中的波
纹可以看作是一个不断向外扩展的圆.
在这一变化过程中的变量是
这两个变量之间的关系是
合作
波纹圆的面积和半径.
波纹圆的面积随着半径的变化而变化;随着半径的确定而确定.
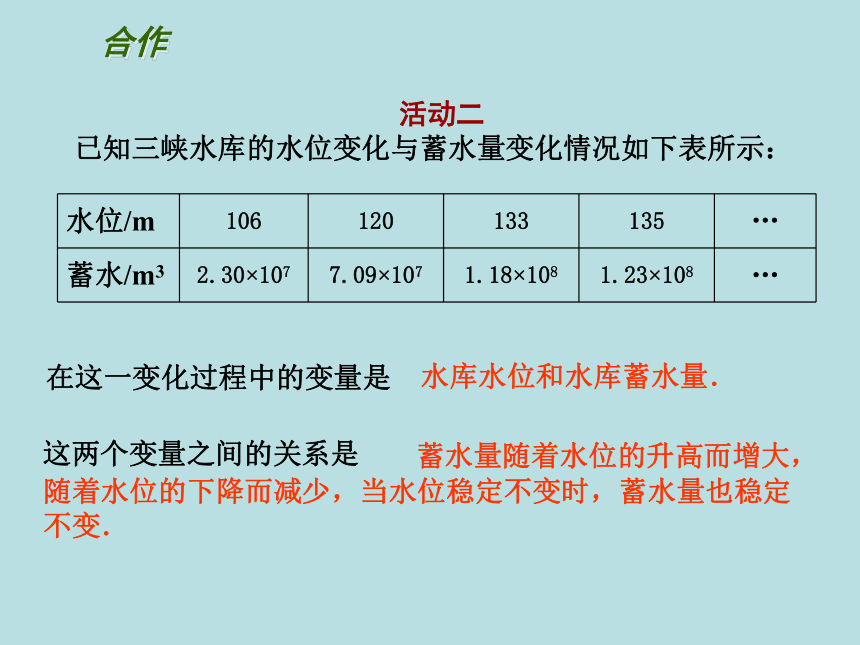
活动二
已知三峡水库的水位变化与蓄水量变化情况如下表所示:
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
在这一变化过程中的变量是
这两个变量之间的关系是
合作
水库水位和水库蓄水量.
蓄水量随着水位的升高而增大,随着水位的下降而减少,当水位稳定不变时,蓄水量也稳定不变.
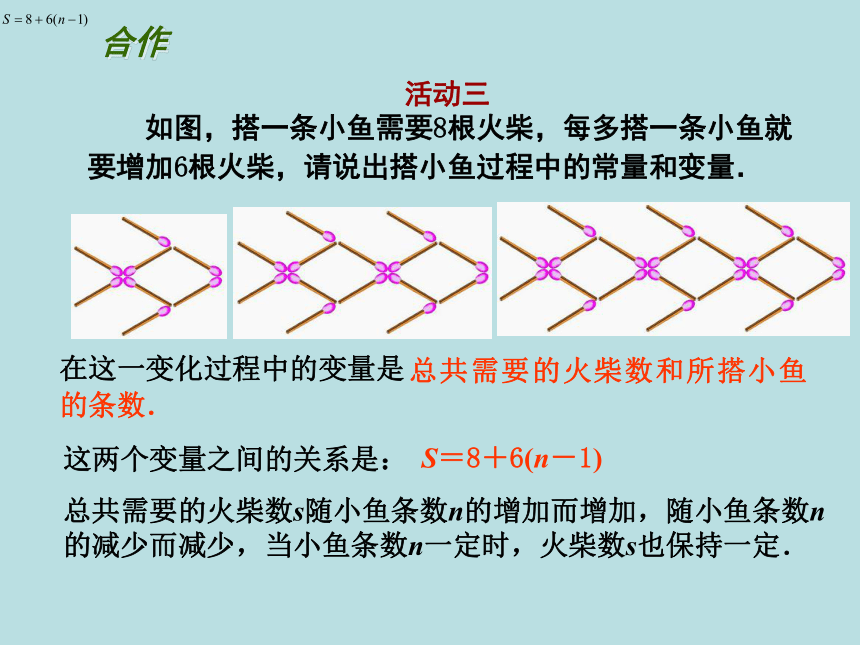
活动三
如图,搭一条小鱼需要8根火柴,每多搭一条小鱼就
要增加6根火柴,请说出搭小鱼过程中的常量和变量.
在这一变化过程中的变量是
这两个变量之间的关系是:
总共需要的火柴数s随小鱼条数n的增加而增加,随小鱼条数n的减少而减少,当小鱼条数n一定时,火柴数s也保持一定.
合作
总共需要的火柴数和所搭小鱼的条数.
S=8+6(n-1)
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
(1)都有两个变量.
(2)当其中一个变量变化时,另一个变量也随着发生变化;当其中一个变量确定时,另一个变量也随着确定.
上面的每个变化过程中有哪些共同之处?
合作
活动四
如图反映的是国庆期间我县某天的温度随时间变化的图象.
探究
随着时间的变化,温度也随之也变化;当时间确定时,温度也随着确定.
一般地,如果在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称
y是x的函数
(functiong)
.其中,x是自变量.
y是因变量.
函数的概念:
戈特弗里德-威廉-莱布尼兹
(德国
1646—1716
)
戈特弗里德·威廉·莱布尼茨(1646—1716),德国哲学家、数学家,和牛顿先后独立发明了微积分。他的著书约四成为拉丁文、约三成为法文、约一成五为德文。他本人是一名律师,经常往返于各大城镇,他许多的公式都是在颠簸的马车上完成的,他也自称具有男爵的贵族身份。莱布尼茨是历史上少见的通才,他所涉及的领域及法学、力学、光学、语言学等40多个范畴,被誉为十七世纪的亚里士多德
。
合作
1.函数是一种对应关系;
2.函数是在一个变化过程中的对应关系;
3.函数的这种对应关系涉及到两个变量;
4.变量x取一个值,变量y只能有唯一的值与之对应.
活动五
小组交流,谈一谈对函数概念的一些认识.
练习
把一根2m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少?
(2)当长方形的宽为0.2m时,长为多少?
(3)这个长方形的长是宽的函数吗?为什么?
解:(3)在这个变化过程中有两个变量“长”
和“宽”;“长”随着“宽”的变化而变化;且对于“宽”的每一个值,“长”都有唯一确定的值与之对应.
所以长方形的长是宽的函数.
展示
1.
y=
例1:
3.y=±x
下列各式中,x都是自变量,请判断
y是不是x的函数,为什么?
4.y=
解:1.
y是x的函数。因为对于x的每一个值,y总有唯一的值与它对应。
2.
y?=x+1
2.
y不是x的函数。
因为当x=3时,y=2
或-2,y有两个值与x对应。
拓展
1.按图示的运算程序,输入一个实数
x
,便可输出一个相应的实数
y
.
(1)y
是
x
的函数吗?为什么?
(2)你能用x的代数式表示y吗?
解.(1)
y
是
x
的函数.当变量
x
变化时,
变量y
总有唯一值与之对应.
(2)y=5(x+2)-4
输入
x
+2
×5
-4
输出
y
2.下列图象中,表示y是x的函数的个数有( )
A.1个
B.2个
C.3个
D.4个
B
3.
弹簧挂上物体后会伸长,测得一个弹簧长度y(㎝)与所挂物体的质量x(㎏)有下面的关系:
x/㎏
0
1
2
3
4
y/㎝
12
12.5
13
13.5
14
根据上述关系,回答下列问题:
(1)弹簧不挂物体时的长度是
㎝
(2)所挂物体的质量为1㎏时,弹簧伸长
㎝
(3)预测挂6㎏的物体时,弹簧的长度(在弹性限度内)
是
㎝
(4)下列各式:①y+x=12;
②x=y-12;
③y=12+0.5x;
④x=12+0.5y.其中,表示弹簧总长y(㎝)与所挂物
体质量x(㎏)之间的关系的式子的是
(填序号)
(5)上式中,有
个变量,
是自变量,变量
是变
量
的函数.
12
0.5
15
③
x
2
x
y
1.
通过这节课的学习,你有哪些收获?
2.本节课,你还有哪些困惑?
评价
(1)首先感受了生活中反映变化过程的几个事例,并从中抽象出常量和变量的概念.
(2)如果在一个变化的过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
变式训练
用总长为60m的篱笆围成矩形场地,求矩形面积S(m2)与一边长L(m
)之间的关系式,
并判断S是否是L的函数。
S=0.5(60-2L)L
=(30-L)L
用60m的篱笆围成矩形,使矩形一边靠墙,另三边用篱笆围成
1.写出矩形面积s(m2)与平行于墙的一边长a(m)的关系式;
2.写出矩形面积s(m2)与垂直于墙的一边长b(m)的关系式。并指出两式中的常量与变量,函数与自变量。
拓展与延伸
墙
a
b
b
60-a
2
S=a
1
S=(60-2b)b
举出你身边函数的例子,并思考它们可以用怎样的形式进行表示?
作业:
6.1 函数(1)
八年级(上册)
初中数学
探究
列车从甲地驶往乙地,在16:17到16:22这个时段,列车在匀速行驶的过程中,哪些量没有变化?哪些量不断变化的?
在这一过程中,没有变化的量是:
列车匀速行驶的速度的数值不变;
从甲地到乙地的路程的数值不变.
在这一过程中,变化了的量是:
列车行驶的时间在不断变化;
列车距离起点和终点的路程也在不断变化.
探究
常量:
在某一变化过程中,数值保持不变的量叫做常量.
变量:
在某一变化过程中,可以取不同数值的量叫做变量.
探究
你还能举出生活中的某些变化过程,并说明其中的常量和变量吗?
展示
请你用有关字母的代数式表示y,并指出其中的常量和变量.
展示
(1)n边形的内角和为y=
.
(2)以30千米/时匀速运动的汽车在t小时行驶的
路程y=
.
(3)圆的半径为r,那么圆的周长y=
.
(4)已知等腰△ABC周长为10cm,
若腰长AB为xcm,
则底边BC长为y
=
.
(n-2)·180°
30t
2πr
5-x
活动一
一石激起千层浪,水滴泛起层层波.变化中的波
纹可以看作是一个不断向外扩展的圆.
在这一变化过程中的变量是
这两个变量之间的关系是
合作
波纹圆的面积和半径.
波纹圆的面积随着半径的变化而变化;随着半径的确定而确定.
活动二
已知三峡水库的水位变化与蓄水量变化情况如下表所示:
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
在这一变化过程中的变量是
这两个变量之间的关系是
合作
水库水位和水库蓄水量.
蓄水量随着水位的升高而增大,随着水位的下降而减少,当水位稳定不变时,蓄水量也稳定不变.
活动三
如图,搭一条小鱼需要8根火柴,每多搭一条小鱼就
要增加6根火柴,请说出搭小鱼过程中的常量和变量.
在这一变化过程中的变量是
这两个变量之间的关系是:
总共需要的火柴数s随小鱼条数n的增加而增加,随小鱼条数n的减少而减少,当小鱼条数n一定时,火柴数s也保持一定.
合作
总共需要的火柴数和所搭小鱼的条数.
S=8+6(n-1)
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
(1)都有两个变量.
(2)当其中一个变量变化时,另一个变量也随着发生变化;当其中一个变量确定时,另一个变量也随着确定.
上面的每个变化过程中有哪些共同之处?
合作
活动四
如图反映的是国庆期间我县某天的温度随时间变化的图象.
探究
随着时间的变化,温度也随之也变化;当时间确定时,温度也随着确定.
一般地,如果在一个变化的过程中有两个变量x和y,如果对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称
y是x的函数
(functiong)
.其中,x是自变量.
y是因变量.
函数的概念:
戈特弗里德-威廉-莱布尼兹
(德国
1646—1716
)
戈特弗里德·威廉·莱布尼茨(1646—1716),德国哲学家、数学家,和牛顿先后独立发明了微积分。他的著书约四成为拉丁文、约三成为法文、约一成五为德文。他本人是一名律师,经常往返于各大城镇,他许多的公式都是在颠簸的马车上完成的,他也自称具有男爵的贵族身份。莱布尼茨是历史上少见的通才,他所涉及的领域及法学、力学、光学、语言学等40多个范畴,被誉为十七世纪的亚里士多德
。
合作
1.函数是一种对应关系;
2.函数是在一个变化过程中的对应关系;
3.函数的这种对应关系涉及到两个变量;
4.变量x取一个值,变量y只能有唯一的值与之对应.
活动五
小组交流,谈一谈对函数概念的一些认识.
练习
把一根2m长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少?
(2)当长方形的宽为0.2m时,长为多少?
(3)这个长方形的长是宽的函数吗?为什么?
解:(3)在这个变化过程中有两个变量“长”
和“宽”;“长”随着“宽”的变化而变化;且对于“宽”的每一个值,“长”都有唯一确定的值与之对应.
所以长方形的长是宽的函数.
展示
1.
y=
例1:
3.y=±x
下列各式中,x都是自变量,请判断
y是不是x的函数,为什么?
4.y=
解:1.
y是x的函数。因为对于x的每一个值,y总有唯一的值与它对应。
2.
y?=x+1
2.
y不是x的函数。
因为当x=3时,y=2
或-2,y有两个值与x对应。
拓展
1.按图示的运算程序,输入一个实数
x
,便可输出一个相应的实数
y
.
(1)y
是
x
的函数吗?为什么?
(2)你能用x的代数式表示y吗?
解.(1)
y
是
x
的函数.当变量
x
变化时,
变量y
总有唯一值与之对应.
(2)y=5(x+2)-4
输入
x
+2
×5
-4
输出
y
2.下列图象中,表示y是x的函数的个数有( )
A.1个
B.2个
C.3个
D.4个
B
3.
弹簧挂上物体后会伸长,测得一个弹簧长度y(㎝)与所挂物体的质量x(㎏)有下面的关系:
x/㎏
0
1
2
3
4
y/㎝
12
12.5
13
13.5
14
根据上述关系,回答下列问题:
(1)弹簧不挂物体时的长度是
㎝
(2)所挂物体的质量为1㎏时,弹簧伸长
㎝
(3)预测挂6㎏的物体时,弹簧的长度(在弹性限度内)
是
㎝
(4)下列各式:①y+x=12;
②x=y-12;
③y=12+0.5x;
④x=12+0.5y.其中,表示弹簧总长y(㎝)与所挂物
体质量x(㎏)之间的关系的式子的是
(填序号)
(5)上式中,有
个变量,
是自变量,变量
是变
量
的函数.
12
0.5
15
③
x
2
x
y
1.
通过这节课的学习,你有哪些收获?
2.本节课,你还有哪些困惑?
评价
(1)首先感受了生活中反映变化过程的几个事例,并从中抽象出常量和变量的概念.
(2)如果在一个变化的过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,x是自变量.
变式训练
用总长为60m的篱笆围成矩形场地,求矩形面积S(m2)与一边长L(m
)之间的关系式,
并判断S是否是L的函数。
S=0.5(60-2L)L
=(30-L)L
用60m的篱笆围成矩形,使矩形一边靠墙,另三边用篱笆围成
1.写出矩形面积s(m2)与平行于墙的一边长a(m)的关系式;
2.写出矩形面积s(m2)与垂直于墙的一边长b(m)的关系式。并指出两式中的常量与变量,函数与自变量。
拓展与延伸
墙
a
b
b
60-a
2
S=a
1
S=(60-2b)b
举出你身边函数的例子,并思考它们可以用怎样的形式进行表示?
作业:
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
