江西省吉水中学2020-2021学年第一学期高二数学(理)11月月考试卷(Word含答案)
文档属性
| 名称 | 江西省吉水中学2020-2021学年第一学期高二数学(理)11月月考试卷(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 760.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览

文档简介
吉水中学2022届高二数学(理)月考试卷
1、已知直线过圆的圆心,且与直线平行,则的方程是( )
A. B.
C. D.
2、记等差数列的前n项和为,若,,则( )
A. B. C. D.0
3、已知,函数的最小值是( )
A.5 B.4 C.8 D.6
4、在△ABC中,cosC=,AC=4,BC=3,则cosB=( )
A. B. C. D.
5、已知、是两条不同的直线,、是两个不同的平面,则下列命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
6、一个正方体纸盒展开后如图所示,在原正方体纸盒中,下列结论:①;②;③MN与AB是异面直线;④BF与CD成角,其中正确的是( )
A.①③ B.②③ C.②④ D.③④
7、已知直三棱柱中,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
8、已知、满足,且目标函数的最大值为,最小值为,则( )
A. B. C. D.
9、已知圆截直线所得弦的长度小于6,则实数的取值范围为( )
A. B. C. D.
10、已知圆和圆的公共弦所在的直线恒过定点,且点在直线上,则的最小值为( )
A. B. C. D.
11、若直线与圆相交,且两个交点位于坐标平面的同一象限,则k的取值范围是( )
A. B. C. D.
12、如图所示,在透明塑料制成的长方体容器内灌进一些水,将容器底面一边固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;②水面四边形的面积不改变;③棱始终与水面平行;④当时,是定值.其中正确说法是( )
A.①②③ B.①③ C.①②③④ D.①③④
二、填空题(4*5=20分)
13、底面边长和高都为2的正四棱锥的表面积为____________.
14、四面体ABCD的四个顶点都在球O的表面上,AB=2,BC=CD=1,∠BCD=60°,AB⊥平面BCD,则球O的表面积为_______.
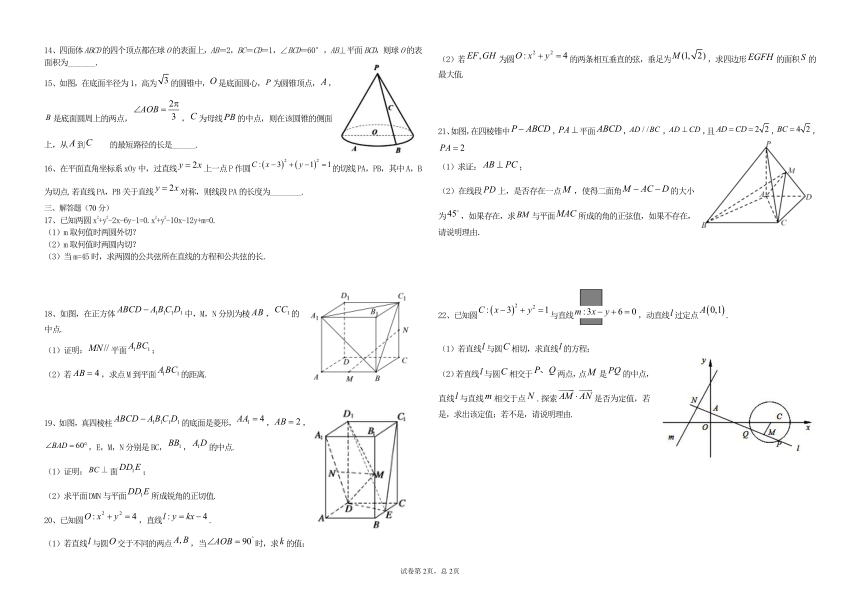
15、如图,在底面半径为1,高为的圆锥中,是底面圆心,为圆锥顶点,,是底面圆周上的两点,,为母线的中点,则在该圆锥的侧面上,从到的最短路径的长是______.
16、在平面直角坐标系xOy中,过直线上一点P作圆的切线PA,PB,其中A,B为切点.若直线PA,PB关于直线对称,则线段PA的长度为________.
三、解答题(70分)
17、已知两圆x2+y2-2x-6y-1=0.x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
18、如图,在正方体中,M,N分別为棱,的中点.
(1)证明:平面;
(2)若,求点M到平面的距离.
19、如图,真四棱柱的底面是菱形,,,,E,M,N分别是BC,,的中点.
(1)证明:面;
(2)求平面DMN与平面所成锐角的正切值.
20、已知圆,直线.
(1)若直线与圆交于不同的两点,当时,求的值;
(2)若为圆的两条相互垂直的弦,垂足为,求四边形的面积的最大值.
21、如图,在四棱锥中,平面,,,且,,
(1)求证:;
(2)在线段上,是否存在一点,使得二面角的大小为,如果存在,求与平面所成的角的正弦值,如果不存在,请说明理由.
22、已知圆与直线,动直线过定点.
(1)若直线与圆相切,求直线的方程;
(2)若直线与圆相交于两点,点是的中点,直线与直线相交于点.探索是否为定值,若是,求出该定值;若不是,请说明理由.
高二数学(理)月考参考答案
一、单项选择
1、D 2、A 3、D 4、A 5、A 6、B 7、B
8、C 9、D 10、C 11、D 12、D
二、填空题
13、 14、 15、 16、2
三、解答题
17、【答案】(1)(2)(3)直线方程为4x+3y-23=0,弦长为
试题解析:(1)由已知可得两个圆的方程分别为(x-1)2+(y-3)2=11、(x-5)2+(y-6)2=61-m,
两圆的圆心距d==5,两圆的半径之和为+,
由两圆的半径之和为+=5,可得m=.
(2)由两圆的圆心距d=="5"等于两圆的半径之差为|-|,
即|-|=5,可得-="5"(舍去),或-=-5,解得m=.
(3)当m=45时,两圆的方程分别为(x-1)2+(y-3)2=11、(x-5)2+(y-6)2=16,
把两个圆的方程相减,可得公共弦所在的直线方程为4x+3y-23=0.
第一个圆的圆心(1,3)到公共弦所在的直线的距离为d==2,可得弦长为
考点:1.两圆相切的位置关系;2.两圆相交的公共弦问题
18、【答案】(1)证明见解析;(2).
详解:(1)证明:取的中点P,连接,,
因为M为的中点,所以,.
又N为的中点,所以,故四边形为平行四边形,则.
又平面,平面,所以平面.
(2)设点M到平面的距离为d,连接,,则,即.
因为,所以,.
则,解得.
故点M到平面的距离为.
19、【答案】(1)证明见解析.(2)
详解:(1)证明:∵在菱形ABCD中,,,且E为BC中点,
∴,∴即,
又棱柱是直四棱柱,∴平面,∴,
又平面,平面,,
∴面;
(2)连接ME,
∵E,M,N分别是BC,,的中点,
∴且,
∴且,∴四边形DNME为平行四边形,
从而可知:DE即为面DMN与面的交线,
∵,,,∴面,
∴且,
则即为平面DMN与平面所成的平面角,
在中,,
故平面DMN与平面所成锐角的正切值为.
20、【答案】(1);(2)5.
【详解】
(1)∵,∴点到直线的距离,
∴,解得.
(2)设圆心到直线,的距离分别为,,则,
而,
∴
,
∴,当且仅当,即时,取等号,
∴四边形的面积的最大值为5.
21、【答案】(1)证明见解析;(2)存在,.
详解:解:(1)如图,由已知得四边形ABCD是直角梯形,
由已知,
可得是等腰直角三角形,即,
又平面ABCD,则,
所以平面PAC,
所以.
(2)假设存在符合条件的点,过点作于,则,
平面,.
过点作于,连接,则平面,
,即是二面角的平面角.
若,则,又,
,即是线段的中点.
存在点使得二面角的大小为.
在三棱锥中,,
设点到平面的距离是,则,
,,
,解得.
在中,,,,,
,
与平面所成角的正弦值为.
22、【答案】(1)或;(2)见解析
【详解】
(1)1°当斜率不存在时,
的方程为,与圆不相切.
2°当的斜率存在时,
设的方程为,即
∴
解得或
∴直线的方程为或
(2)有(1)可知的斜率存在,
设的方程为,
由消去后得
∴,
∴∴
由得
∴∴
∴
∴为定值.
试卷第2 22页,总2 22页
试卷第1 11页,总2 22页
答案第2 22页,总2 22页
答案第1 11页,总2 22页
1、已知直线过圆的圆心,且与直线平行,则的方程是( )
A. B.
C. D.
2、记等差数列的前n项和为,若,,则( )
A. B. C. D.0
3、已知,函数的最小值是( )
A.5 B.4 C.8 D.6
4、在△ABC中,cosC=,AC=4,BC=3,则cosB=( )
A. B. C. D.
5、已知、是两条不同的直线,、是两个不同的平面,则下列命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
6、一个正方体纸盒展开后如图所示,在原正方体纸盒中,下列结论:①;②;③MN与AB是异面直线;④BF与CD成角,其中正确的是( )
A.①③ B.②③ C.②④ D.③④
7、已知直三棱柱中,,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
8、已知、满足,且目标函数的最大值为,最小值为,则( )
A. B. C. D.
9、已知圆截直线所得弦的长度小于6,则实数的取值范围为( )
A. B. C. D.
10、已知圆和圆的公共弦所在的直线恒过定点,且点在直线上,则的最小值为( )
A. B. C. D.
11、若直线与圆相交,且两个交点位于坐标平面的同一象限,则k的取值范围是( )
A. B. C. D.
12、如图所示,在透明塑料制成的长方体容器内灌进一些水,将容器底面一边固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;②水面四边形的面积不改变;③棱始终与水面平行;④当时,是定值.其中正确说法是( )
A.①②③ B.①③ C.①②③④ D.①③④
二、填空题(4*5=20分)
13、底面边长和高都为2的正四棱锥的表面积为____________.
14、四面体ABCD的四个顶点都在球O的表面上,AB=2,BC=CD=1,∠BCD=60°,AB⊥平面BCD,则球O的表面积为_______.
15、如图,在底面半径为1,高为的圆锥中,是底面圆心,为圆锥顶点,,是底面圆周上的两点,,为母线的中点,则在该圆锥的侧面上,从到的最短路径的长是______.
16、在平面直角坐标系xOy中,过直线上一点P作圆的切线PA,PB,其中A,B为切点.若直线PA,PB关于直线对称,则线段PA的长度为________.
三、解答题(70分)
17、已知两圆x2+y2-2x-6y-1=0.x2+y2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
18、如图,在正方体中,M,N分別为棱,的中点.
(1)证明:平面;
(2)若,求点M到平面的距离.
19、如图,真四棱柱的底面是菱形,,,,E,M,N分别是BC,,的中点.
(1)证明:面;
(2)求平面DMN与平面所成锐角的正切值.
20、已知圆,直线.
(1)若直线与圆交于不同的两点,当时,求的值;
(2)若为圆的两条相互垂直的弦,垂足为,求四边形的面积的最大值.
21、如图,在四棱锥中,平面,,,且,,
(1)求证:;
(2)在线段上,是否存在一点,使得二面角的大小为,如果存在,求与平面所成的角的正弦值,如果不存在,请说明理由.
22、已知圆与直线,动直线过定点.
(1)若直线与圆相切,求直线的方程;
(2)若直线与圆相交于两点,点是的中点,直线与直线相交于点.探索是否为定值,若是,求出该定值;若不是,请说明理由.
高二数学(理)月考参考答案
一、单项选择
1、D 2、A 3、D 4、A 5、A 6、B 7、B
8、C 9、D 10、C 11、D 12、D
二、填空题
13、 14、 15、 16、2
三、解答题
17、【答案】(1)(2)(3)直线方程为4x+3y-23=0,弦长为
试题解析:(1)由已知可得两个圆的方程分别为(x-1)2+(y-3)2=11、(x-5)2+(y-6)2=61-m,
两圆的圆心距d==5,两圆的半径之和为+,
由两圆的半径之和为+=5,可得m=.
(2)由两圆的圆心距d=="5"等于两圆的半径之差为|-|,
即|-|=5,可得-="5"(舍去),或-=-5,解得m=.
(3)当m=45时,两圆的方程分别为(x-1)2+(y-3)2=11、(x-5)2+(y-6)2=16,
把两个圆的方程相减,可得公共弦所在的直线方程为4x+3y-23=0.
第一个圆的圆心(1,3)到公共弦所在的直线的距离为d==2,可得弦长为
考点:1.两圆相切的位置关系;2.两圆相交的公共弦问题
18、【答案】(1)证明见解析;(2).
详解:(1)证明:取的中点P,连接,,
因为M为的中点,所以,.
又N为的中点,所以,故四边形为平行四边形,则.
又平面,平面,所以平面.
(2)设点M到平面的距离为d,连接,,则,即.
因为,所以,.
则,解得.
故点M到平面的距离为.
19、【答案】(1)证明见解析.(2)
详解:(1)证明:∵在菱形ABCD中,,,且E为BC中点,
∴,∴即,
又棱柱是直四棱柱,∴平面,∴,
又平面,平面,,
∴面;
(2)连接ME,
∵E,M,N分别是BC,,的中点,
∴且,
∴且,∴四边形DNME为平行四边形,
从而可知:DE即为面DMN与面的交线,
∵,,,∴面,
∴且,
则即为平面DMN与平面所成的平面角,
在中,,
故平面DMN与平面所成锐角的正切值为.
20、【答案】(1);(2)5.
【详解】
(1)∵,∴点到直线的距离,
∴,解得.
(2)设圆心到直线,的距离分别为,,则,
而,
∴
,
∴,当且仅当,即时,取等号,
∴四边形的面积的最大值为5.
21、【答案】(1)证明见解析;(2)存在,.
详解:解:(1)如图,由已知得四边形ABCD是直角梯形,
由已知,
可得是等腰直角三角形,即,
又平面ABCD,则,
所以平面PAC,
所以.
(2)假设存在符合条件的点,过点作于,则,
平面,.
过点作于,连接,则平面,
,即是二面角的平面角.
若,则,又,
,即是线段的中点.
存在点使得二面角的大小为.
在三棱锥中,,
设点到平面的距离是,则,
,,
,解得.
在中,,,,,
,
与平面所成角的正弦值为.
22、【答案】(1)或;(2)见解析
【详解】
(1)1°当斜率不存在时,
的方程为,与圆不相切.
2°当的斜率存在时,
设的方程为,即
∴
解得或
∴直线的方程为或
(2)有(1)可知的斜率存在,
设的方程为,
由消去后得
∴,
∴∴
由得
∴∴
∴
∴为定值.
试卷第2 22页,总2 22页
试卷第1 11页,总2 22页
答案第2 22页,总2 22页
答案第1 11页,总2 22页
同课章节目录
