人教版八年级下册 19.2.1 正比例函数与一次函数的图像和性质教案
文档属性
| 名称 | 人教版八年级下册 19.2.1 正比例函数与一次函数的图像和性质教案 | 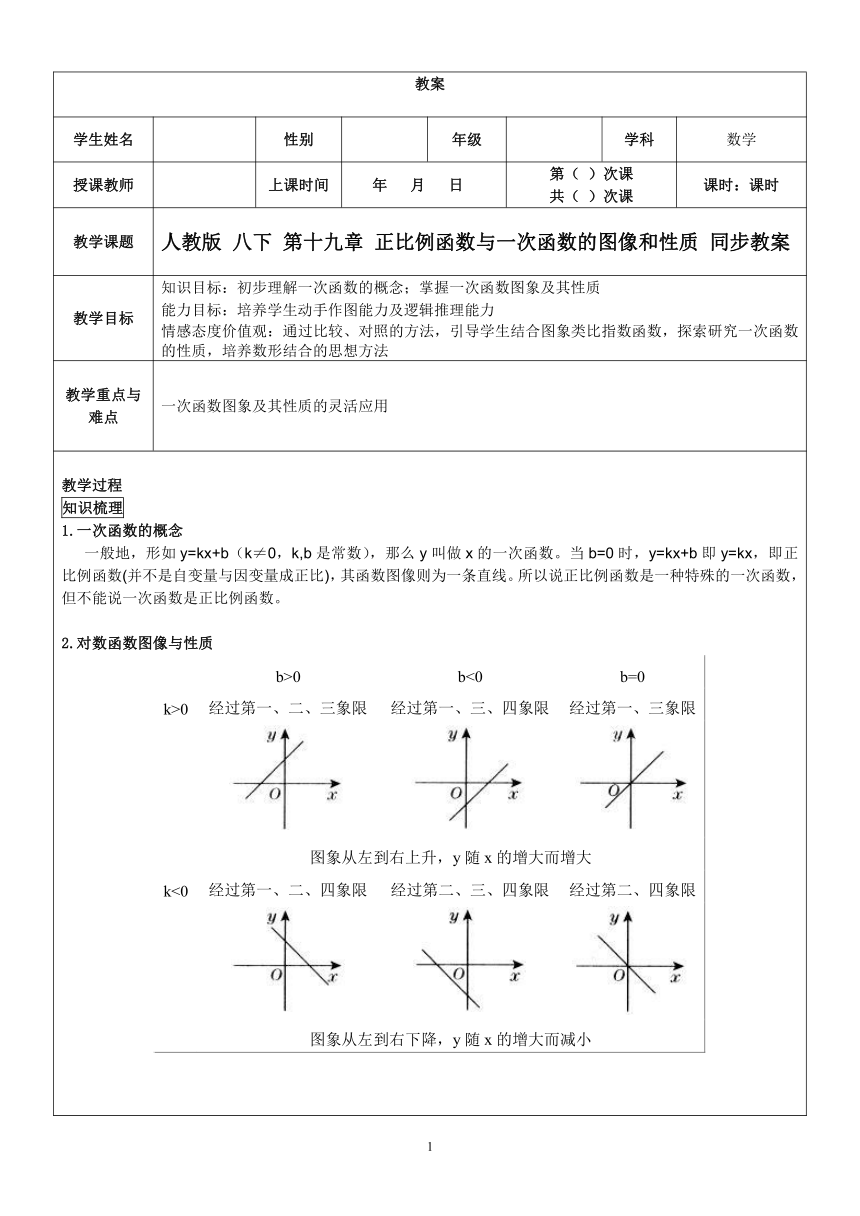 | |
| 格式 | zip | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 19:14:30 | ||
图片预览



文档简介
教案
学生姓名
性别
年级
学科
数学
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:课时
教学课题
人教版
八下
第十九章
正比例函数与一次函数的图像和性质
同步教案
教学目标
知识目标:初步理解一次函数的概念;掌握一次函数图象及其性质
能力目标:培养学生动手作图能力及逻辑推理能力
情感态度价值观:通过比较、对照的方法,引导学生结合图象类比指数函数,探索研究一次函数的性质,培养数形结合的思想方法
教学重点与难点
一次函数图象及其性质的灵活应用
教学过程
知识梳理
1.一次函数的概念
一般地,形如y=kx+b(k≠0,k,b是常数),那么y叫做x的一次函数。当b=0时,y=kx+b即y=kx,即正比例函数(并不是自变量与因变量成正比),其函数图像则为一条直线。所以说正比例函数是一种特殊的一次函数,但不能说一次函数是正比例函数。
2.对数函数图像与性质
b>0b<0b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y随x的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y随x的增大而减小
直线y1=kx+b与y2=kx图象的位置关系:
(1)当b>0时,将y2=kx图象向x轴上方平移b个单位,就得到y1=kx+b的图象.
当b<0时,将y2=kx图象向x轴下方平移-b个单位,就得到了y1=kx+b的图象.
4、直线l1:y1=k1x+b1与l2:y2=k2x+b2的位置关系可由其解析式中的比例系数和常数来确定:
当k1≠k2时,l1与l2相交,交点是(0,b).
5、直线y=kx+b(k≠0)与坐标轴的交点.
(1)直线y=kx与x轴、y轴的交点都是(0,0);
(2)直线y=kx+b与x轴交点坐标为(,0)与
y轴交点坐标为(0,b).
6、用待定系数法确定函数解析式的一般步骤:
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.
例题精讲
已知点(3,m)与点(n,-2)关于坐标系原点对称,则mn=_______
点A为直线y=-2x+2上的一点,且到两坐标轴距离相等,那么A点坐标为_____
已知y=3x+4当x_______时,函数值为正数
函数函数与x轴交点坐标为_________
某种储蓄的月利率是0.25%,存入200元本金后,则本息和y元与所存月数x之间函数关系式为_______________
直线y=-3x-1与坐标轴围成三角形面积为________
在函数的表达式中,自变量x取值范围是______________
若函数图象如图所示,
则不等式解集为__________
选择题(每题4分,计28分)
1、如果直线经过第一、二、四象限,则m的取值范围是(
)
A、m<2
B、m>1
C、m≠2
D、12、一次函数和的图象的交点个数为(
)
A、没有
B、一个
C、两个
D、无数个
3、汽车由重庆驶往相距400千米的成都,如果汽车的平均速度是100千米/时,那么汽车距成都的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为(
)
A
B
C
D
4、已知函数,当自变量x增加m时,相应函数值增加(
)
A、3m+1
B、3m
C、m
D、3m-1
5、若点A(-2,n)在x轴上,则B(n-1,n+1)在(
)
A、第一象限
B、第二象限
C、第三象限
D、第四象限
6、m为整数,点P(3m-9,3-3m)是第三象限的点,则P点的坐标为(
)
A、(-3,-3)
B、(-3,-2)
C、(-2,-2)
D、(-2,-3)
7、观察下列图象,可以得出不等式组
的解集是(
)
A、
B、
C、
D、
三、解答题(每题10分,计40分)
1、已知一次函数的图象经过(2,5)和(-1,-1)两点,(1)在给定坐标系中画出这个函数图象;(2)求这个一次函数解析式
2、某校需要刻录一批电脑光盘,若电脑公司刻录,每张需要8元(含空白光盘费);若学校自刻,除租用刻录机需120元外每张还需成本费4元(含空白光盘费),问刻录这批电脑光盘,到电脑公司刻录费用少?还是自刻费用少?说明你的理由
3、有两条直线,,学生甲解出它们的交点坐标为(3,-2),学生乙因把c抄错了而解出它们的交点坐标为,求这两条直线解析式
4、已知正比例函数的图象与一次函数的图象交于点P(3,-6)
(1)求的值
(2)如果一次函数与x轴交于点A,求A点坐标
5.我市某乡A\B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B运往C、D两处的费用分别为每吨15元和18元。设从A运往C仓库的柑橘质量为X吨,A、B两村运往两仓库的柑橘运输费用为Ya和Yb元。
(1)填写下表,并求出Ya和Yb与X之间的函数关系式。
收地
产地CD总计AX吨200吨B300吨总计240吨260吨500吨
(2)试讨论A、B两村中,哪个村的运费较少?
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元,在各种情况下,问该怎样调运,才能使两村运费之和最少?求出这个最小值。
学生姓名
性别
年级
学科
数学
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:课时
教学课题
人教版
八下
第十九章
正比例函数与一次函数的图像和性质
同步教案
教学目标
知识目标:初步理解一次函数的概念;掌握一次函数图象及其性质
能力目标:培养学生动手作图能力及逻辑推理能力
情感态度价值观:通过比较、对照的方法,引导学生结合图象类比指数函数,探索研究一次函数的性质,培养数形结合的思想方法
教学重点与难点
一次函数图象及其性质的灵活应用
教学过程
知识梳理
1.一次函数的概念
一般地,形如y=kx+b(k≠0,k,b是常数),那么y叫做x的一次函数。当b=0时,y=kx+b即y=kx,即正比例函数(并不是自变量与因变量成正比),其函数图像则为一条直线。所以说正比例函数是一种特殊的一次函数,但不能说一次函数是正比例函数。
2.对数函数图像与性质
b>0b<0b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y随x的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y随x的增大而减小
直线y1=kx+b与y2=kx图象的位置关系:
(1)当b>0时,将y2=kx图象向x轴上方平移b个单位,就得到y1=kx+b的图象.
当b<0时,将y2=kx图象向x轴下方平移-b个单位,就得到了y1=kx+b的图象.
4、直线l1:y1=k1x+b1与l2:y2=k2x+b2的位置关系可由其解析式中的比例系数和常数来确定:
当k1≠k2时,l1与l2相交,交点是(0,b).
5、直线y=kx+b(k≠0)与坐标轴的交点.
(1)直线y=kx与x轴、y轴的交点都是(0,0);
(2)直线y=kx+b与x轴交点坐标为(,0)与
y轴交点坐标为(0,b).
6、用待定系数法确定函数解析式的一般步骤:
(1)根据已知条件写出含有待定系数的函数关系式;
(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;
(3)解方程得出未知系数的值;
(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式.
例题精讲
已知点(3,m)与点(n,-2)关于坐标系原点对称,则mn=_______
点A为直线y=-2x+2上的一点,且到两坐标轴距离相等,那么A点坐标为_____
已知y=3x+4当x_______时,函数值为正数
函数函数与x轴交点坐标为_________
某种储蓄的月利率是0.25%,存入200元本金后,则本息和y元与所存月数x之间函数关系式为_______________
直线y=-3x-1与坐标轴围成三角形面积为________
在函数的表达式中,自变量x取值范围是______________
若函数图象如图所示,
则不等式解集为__________
选择题(每题4分,计28分)
1、如果直线经过第一、二、四象限,则m的取值范围是(
)
A、m<2
B、m>1
C、m≠2
D、1
)
A、没有
B、一个
C、两个
D、无数个
3、汽车由重庆驶往相距400千米的成都,如果汽车的平均速度是100千米/时,那么汽车距成都的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为(
)
A
B
C
D
4、已知函数,当自变量x增加m时,相应函数值增加(
)
A、3m+1
B、3m
C、m
D、3m-1
5、若点A(-2,n)在x轴上,则B(n-1,n+1)在(
)
A、第一象限
B、第二象限
C、第三象限
D、第四象限
6、m为整数,点P(3m-9,3-3m)是第三象限的点,则P点的坐标为(
)
A、(-3,-3)
B、(-3,-2)
C、(-2,-2)
D、(-2,-3)
7、观察下列图象,可以得出不等式组
的解集是(
)
A、
B、
C、
D、
三、解答题(每题10分,计40分)
1、已知一次函数的图象经过(2,5)和(-1,-1)两点,(1)在给定坐标系中画出这个函数图象;(2)求这个一次函数解析式
2、某校需要刻录一批电脑光盘,若电脑公司刻录,每张需要8元(含空白光盘费);若学校自刻,除租用刻录机需120元外每张还需成本费4元(含空白光盘费),问刻录这批电脑光盘,到电脑公司刻录费用少?还是自刻费用少?说明你的理由
3、有两条直线,,学生甲解出它们的交点坐标为(3,-2),学生乙因把c抄错了而解出它们的交点坐标为,求这两条直线解析式
4、已知正比例函数的图象与一次函数的图象交于点P(3,-6)
(1)求的值
(2)如果一次函数与x轴交于点A,求A点坐标
5.我市某乡A\B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B运往C、D两处的费用分别为每吨15元和18元。设从A运往C仓库的柑橘质量为X吨,A、B两村运往两仓库的柑橘运输费用为Ya和Yb元。
(1)填写下表,并求出Ya和Yb与X之间的函数关系式。
收地
产地CD总计AX吨200吨B300吨总计240吨260吨500吨
(2)试讨论A、B两村中,哪个村的运费较少?
(3)考虑到B村的经济承受能力,B村的柑橘运费不得超过4830元,在各种情况下,问该怎样调运,才能使两村运费之和最少?求出这个最小值。
