沪教版(上海)数学八年级下册 20.1 一次函数的概念—变量与函数课件(共21张PPT)
文档属性
| 名称 | 沪教版(上海)数学八年级下册 20.1 一次函数的概念—变量与函数课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
18.1
函数的概念
——变量与函数
人们在认识和描述某一事物时,经常会用“量
”来具体表达事物的某些特征(属性)
,同时用“数
”来表明量的大小,数与度量单位合在一起,就是“数量
”
乌鸦喝水
有一只乌鸦特别聪明,智慧过人。一天,它干完活又累又渴,真想喝水。忽然,它看一只大水罐,满心欢喜。它飞到水罐旁,一看罐里的水不多了,嘴探进去也喝不到,怎么办呢?它使劲地用身体撞水罐,又用翅膀推水罐,想把水罐弄倒,好喝水。可是水罐又大又重,它的力量太小了,弄不倒这罐子。忽然,它急中生智,可以叼些石子放到罐里,石子多了,罐子里的水不就升高了吗?这么想,就这么做了,它不厌其烦地一块一块地用嘴叼石子,功夫不负有心的乌鸦,在它终于放了很多石子后,水上升了,乌鸦喝到了水,它痛痛快快地喝了个够,解了渴。
在从南京到上海的动车组列车上,有几位同学谈论着南京到上海的距离、行驶的速度和行驶的时间。
在这一过程中哪些量没有发生变化?哪些量发生变化?
南京到上海的距离
列车行驶的时间和行驶的速度
像这样保持数值不变的量叫做常量
像这样可以取不同数值的量叫做变量
1.圆的周长C和半径r之间的关系式是
,其中变量是
常量是
。
2.
直角三角形两个锐角的度数是x
、
y,其关系式是y=90-x,其中变量是
,常量是 。
C,
r
2,π
y,x
90
填空:
工作人员将水库的水位变化与水库蓄水量变化情况列成如下表格:
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
(1)表格中出现了几个变量?
(2)当水位的高度发生变化时,蓄水量是否也在变化?
问题1
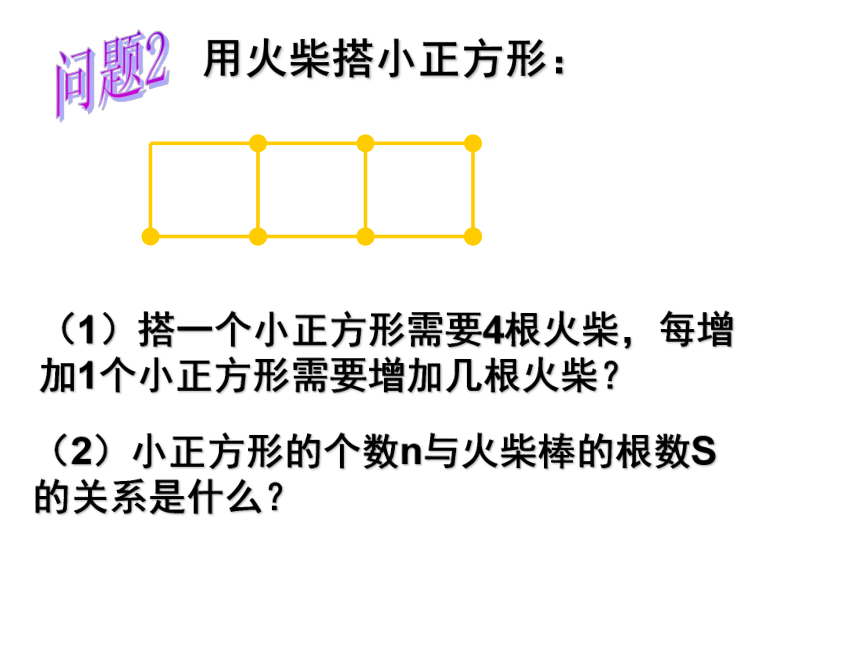
(1)搭一个小正方形需要4根火柴,每增加1个小正方形需要增加几根火柴?
(2)小正方形的个数n与火柴棒的根数S的关系是什么?
用火柴搭小正方形:
问题2
你坐过摩天轮吗?你坐在摩天轮上时,随着时间的变化,你离开地面的高度是如何变化的?
问题3
下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
问题:当t=2分时,对应的高度h=?
那么t=3分时呢?
问题二:搭n个小正方形与所需的火柴根数S之间的关系
问题一:水库的水位变化与水库蓄水量变化情况
问题三:旋转时间t与摩天轮上一点的高度h之间的关系
在某个变化过程中有
,设为x和y,如果在变量x的
内,变量y随着x的变化而变化,它们之间存在确定的
,那么变量y叫做变量x的
。
其中x叫做自变量。
两个变量
允许取值范围
依赖关系
函数
某地一天的气温变化图
1、判断:下列各题中,哪些是函数关系,哪些不是函数关系
(1)已知物体匀速运动中,路程s、速度v、时间t之间有关系式s=vt。若速度不变,路程s是时间t的函数吗?
(2)某校学生总人数1200人,某天学生的出勤率p是实际到校学生人数n的函数吗?(
)
(3)变量x+2是变量x的函数吗?
(4)学生的身高是数学成绩的函数吗?
(5)正方形的面积是边长的函数吗?
2、如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与垂足D不重合),分别联结CA、CB,得到△ABC。
(1)指出在△ABC的面积变化过程中,线段AB、CD的长哪一个是常量?哪一个是变量?
(2)设CD的长为h,△ABC的面积为S,S是不是h的函数?
A
D
B
C
E
3、用一根1m长的铁丝围成一个长方形,设长方形的宽为x,长为y
(1)当x=0.1m时,y是多少?
(2)当x=0.2m时,y是多少?
(3)由上可知,谁是谁的函数?
本节课我们学习主要内容是什么?
你有什么收获?
本课小结
你还有哪些困惑?
1、五个概念:常量、变量、函数、自变量、函数解析式
2、两个注意:(1)判断常量与变量
(2)判断函数关系
下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
问题:当h=35米时,t=?
1、什么叫变量?什么叫常量?
2、什么叫函数?在一个变化过程中有
两个变量,这两个变量一定是函数关系吗?为什么?
回顾与思考
3、下列说法中,不正确的是(
)
A、函数不是数,而是
一种关系
B、多边形的内角和是边数的函数
C、一天中时间是温度的函数
D、一天中温度是时间的函数
C
小红的爷爷饭后出去散步,从家里出发走20分钟到一个离家900米的街心花园与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家距离y(米)与时间x(分)之间函数关系的是(
)
y(米)
X(分)
20
40
o
900
y(米)
X(分)
20
40
o
B
900
y(米)
X(分)
20
40
o
C
900
y(米)
X(分)
20
40
o
D
900
A
D
回顾与思考
18.1
函数的概念
——变量与函数
人们在认识和描述某一事物时,经常会用“量
”来具体表达事物的某些特征(属性)
,同时用“数
”来表明量的大小,数与度量单位合在一起,就是“数量
”
乌鸦喝水
有一只乌鸦特别聪明,智慧过人。一天,它干完活又累又渴,真想喝水。忽然,它看一只大水罐,满心欢喜。它飞到水罐旁,一看罐里的水不多了,嘴探进去也喝不到,怎么办呢?它使劲地用身体撞水罐,又用翅膀推水罐,想把水罐弄倒,好喝水。可是水罐又大又重,它的力量太小了,弄不倒这罐子。忽然,它急中生智,可以叼些石子放到罐里,石子多了,罐子里的水不就升高了吗?这么想,就这么做了,它不厌其烦地一块一块地用嘴叼石子,功夫不负有心的乌鸦,在它终于放了很多石子后,水上升了,乌鸦喝到了水,它痛痛快快地喝了个够,解了渴。
在从南京到上海的动车组列车上,有几位同学谈论着南京到上海的距离、行驶的速度和行驶的时间。
在这一过程中哪些量没有发生变化?哪些量发生变化?
南京到上海的距离
列车行驶的时间和行驶的速度
像这样保持数值不变的量叫做常量
像这样可以取不同数值的量叫做变量
1.圆的周长C和半径r之间的关系式是
,其中变量是
常量是
。
2.
直角三角形两个锐角的度数是x
、
y,其关系式是y=90-x,其中变量是
,常量是 。
C,
r
2,π
y,x
90
填空:
工作人员将水库的水位变化与水库蓄水量变化情况列成如下表格:
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
(1)表格中出现了几个变量?
(2)当水位的高度发生变化时,蓄水量是否也在变化?
问题1
(1)搭一个小正方形需要4根火柴,每增加1个小正方形需要增加几根火柴?
(2)小正方形的个数n与火柴棒的根数S的关系是什么?
用火柴搭小正方形:
问题2
你坐过摩天轮吗?你坐在摩天轮上时,随着时间的变化,你离开地面的高度是如何变化的?
问题3
下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
问题:当t=2分时,对应的高度h=?
那么t=3分时呢?
问题二:搭n个小正方形与所需的火柴根数S之间的关系
问题一:水库的水位变化与水库蓄水量变化情况
问题三:旋转时间t与摩天轮上一点的高度h之间的关系
在某个变化过程中有
,设为x和y,如果在变量x的
内,变量y随着x的变化而变化,它们之间存在确定的
,那么变量y叫做变量x的
。
其中x叫做自变量。
两个变量
允许取值范围
依赖关系
函数
某地一天的气温变化图
1、判断:下列各题中,哪些是函数关系,哪些不是函数关系
(1)已知物体匀速运动中,路程s、速度v、时间t之间有关系式s=vt。若速度不变,路程s是时间t的函数吗?
(2)某校学生总人数1200人,某天学生的出勤率p是实际到校学生人数n的函数吗?(
)
(3)变量x+2是变量x的函数吗?
(4)学生的身高是数学成绩的函数吗?
(5)正方形的面积是边长的函数吗?
2、如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与垂足D不重合),分别联结CA、CB,得到△ABC。
(1)指出在△ABC的面积变化过程中,线段AB、CD的长哪一个是常量?哪一个是变量?
(2)设CD的长为h,△ABC的面积为S,S是不是h的函数?
A
D
B
C
E
3、用一根1m长的铁丝围成一个长方形,设长方形的宽为x,长为y
(1)当x=0.1m时,y是多少?
(2)当x=0.2m时,y是多少?
(3)由上可知,谁是谁的函数?
本节课我们学习主要内容是什么?
你有什么收获?
本课小结
你还有哪些困惑?
1、五个概念:常量、变量、函数、自变量、函数解析式
2、两个注意:(1)判断常量与变量
(2)判断函数关系
下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
问题:当h=35米时,t=?
1、什么叫变量?什么叫常量?
2、什么叫函数?在一个变化过程中有
两个变量,这两个变量一定是函数关系吗?为什么?
回顾与思考
3、下列说法中,不正确的是(
)
A、函数不是数,而是
一种关系
B、多边形的内角和是边数的函数
C、一天中时间是温度的函数
D、一天中温度是时间的函数
C
小红的爷爷饭后出去散步,从家里出发走20分钟到一个离家900米的街心花园与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家距离y(米)与时间x(分)之间函数关系的是(
)
y(米)
X(分)
20
40
o
900
y(米)
X(分)
20
40
o
B
900
y(米)
X(分)
20
40
o
C
900
y(米)
X(分)
20
40
o
D
900
A
D
回顾与思考
