人教版数学八年级上册12.2三角形全等的判定测试题(三)(word版含答案)
文档属性
| 名称 | 人教版数学八年级上册12.2三角形全等的判定测试题(三)(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览

文档简介
12.2三角形全等的判定测试题(三)及答案
一. 选择题:
1. 如图在△ABD和△ACE都是等边三角形,则的根据是( )
A. SSS B. SAS C. ASA D. AAS
2. 在和中,下列各组条件中,不能保证:的是( )
① ② ③
④ ⑤ ⑥
A. 具备①②③ B. 具备①②④
C. 具备③④⑤ D. 具备②③⑥
3. 如图,AB∥CD,AD∥BC,OE=OF,则图中全等三角形的组数是( )
A. 3 B. 4 C. 5 D. 6
4. 如图AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是( )
A. B.
C. D.
5. 两个三角形只有以下元素对应相等,不能判定两个三角形全等的是( )
A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边
6. 如果两个三角形两边对应相等,且其中一边所对的角也相等,那么这两个三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 面积相等
7. 如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A. 相等 B. 不相等 C. 互余或相等 D. 互补或相等
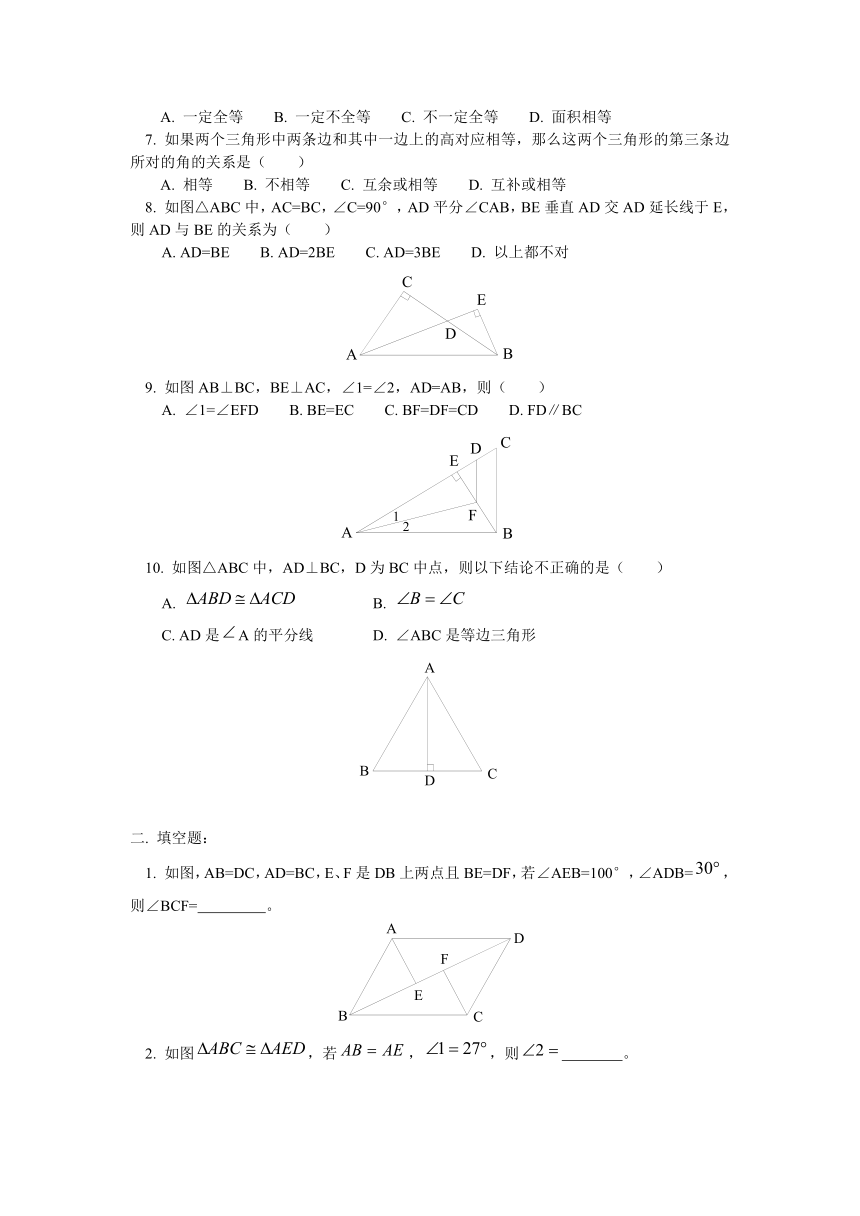
8. 如图△ABC中,AC=BC,∠C=90°,AD平分∠CAB,BE垂直AD交AD延长线于E,则AD与BE的关系为( )
A. AD=BE B. AD=2BE C. AD=3BE D. 以上都不对
9. 如图AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
A. ∠1=∠EFD B. BE=EC C. BF=DF=CD D. FD∥BC
10. 如图△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )
A. B.
C. AD是A的平分线 D. ∠ABC是等边三角形
?
二. 填空题:
1. 如图,AB=DC,AD=BC,E、F是DB上两点且BE=DF,若∠AEB=100°,∠ADB=,则∠BCF= 。
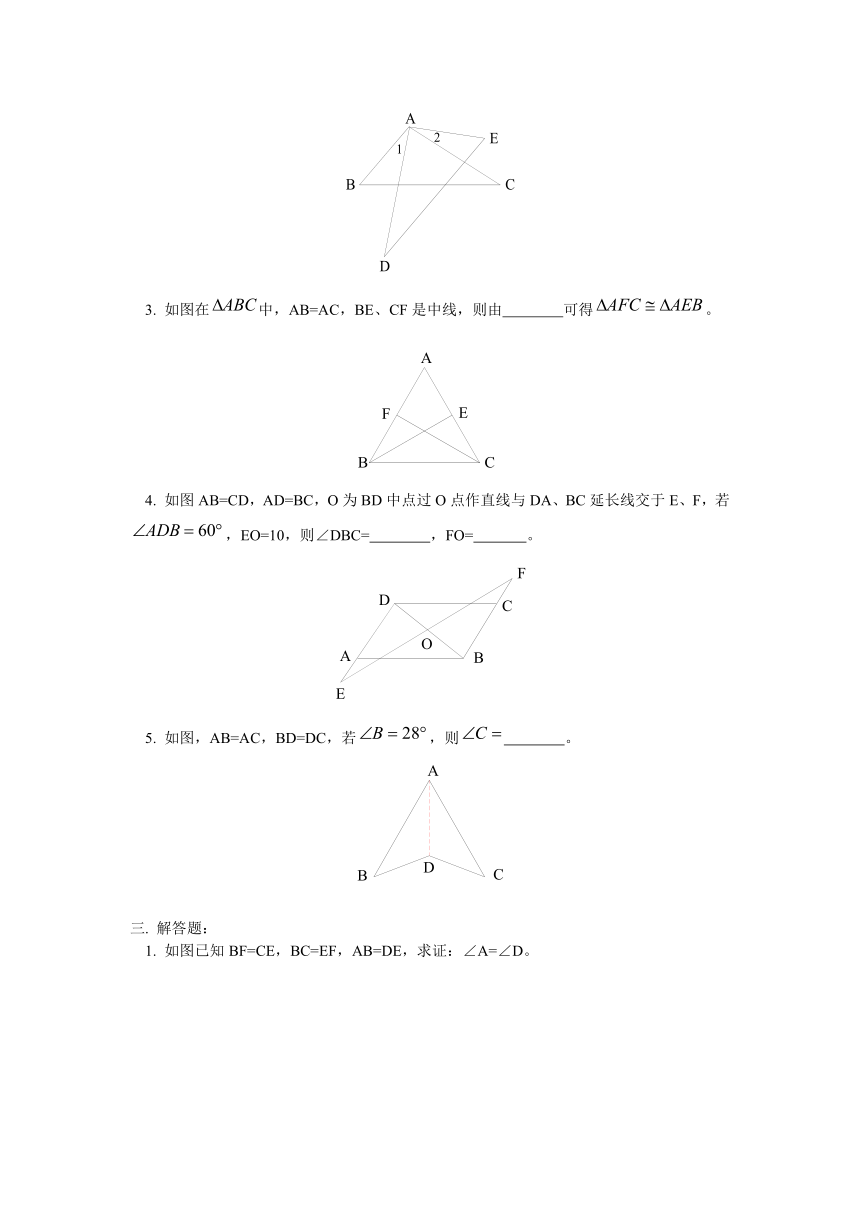
2. 如图,若,,则 。
3. 如图在中,AB=AC,BE、CF是中线,则由 可得。
4. 如图AB=CD,AD=BC,O为BD中点过O点作直线与DA、BC延长线交于E、F,若,EO=10,则∠DBC= ,FO= 。
5. 如图,AB=AC,BD=DC,若,则 。
?
三. 解答题:
1. 如图已知BF=CE,BC=EF,AB=DE,求证:∠A=∠D。
2. 如图OA=OB,点C、D分别在OA、OB上,且OC=OD,AD、BC交于E,求证:OE平分∠AOB。
3. 已知AC、EF相交于O,且AO=CO,BO=DO,EO=OF,求证:。
4. 已知∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,求证:AB=ED。
?
?
答案
一.
1. B 2. B 3. D 4. A 5. C 6. C 7. D 8. B 9. D 10. D
?
二.
1. 70° 2. 27° 3. SAS 4. 60°;10 5. 28°
?
二.
1.
证明:连结FC,在与中, ∴ (SSS)
∴ ∠1=∠2、∠3=∠4(全等三角形对应角相等)
∴ ∠EFB=∠BCE 又 ∵ AB=ED ∴ AC=FD
在△FDB与△ACE中 ∴ (SAS)
∴ (全等三角形对应角相等)
2.
证明:在与中, ∴ (SAS)
∴ 、(全等三角形对应角相等) ∴ AC=DB
在与中 ∴ (AAS)
∴ AE=EB 在与中,
∴ (SSS) ∴ ∴ OE平分∠AOB
3.
证明:在与中, ∴ (SAS)
∴ AE=FC 同理
BE=FD ∴
在与中, ∴ (SAS)
4.
证明:延长BA、CE交于G,在中,
在中, ∵
∴ ∴
∴ ∴ 在与中
∴ (AAS)
∴ AB=ED(全等三角形对应边相等)
一. 选择题:
1. 如图在△ABD和△ACE都是等边三角形,则的根据是( )
A. SSS B. SAS C. ASA D. AAS
2. 在和中,下列各组条件中,不能保证:的是( )
① ② ③
④ ⑤ ⑥
A. 具备①②③ B. 具备①②④
C. 具备③④⑤ D. 具备②③⑥
3. 如图,AB∥CD,AD∥BC,OE=OF,则图中全等三角形的组数是( )
A. 3 B. 4 C. 5 D. 6
4. 如图AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是( )
A. B.
C. D.
5. 两个三角形只有以下元素对应相等,不能判定两个三角形全等的是( )
A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边
6. 如果两个三角形两边对应相等,且其中一边所对的角也相等,那么这两个三角形( )
A. 一定全等 B. 一定不全等 C. 不一定全等 D. 面积相等
7. 如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A. 相等 B. 不相等 C. 互余或相等 D. 互补或相等
8. 如图△ABC中,AC=BC,∠C=90°,AD平分∠CAB,BE垂直AD交AD延长线于E,则AD与BE的关系为( )
A. AD=BE B. AD=2BE C. AD=3BE D. 以上都不对
9. 如图AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则( )
A. ∠1=∠EFD B. BE=EC C. BF=DF=CD D. FD∥BC
10. 如图△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )
A. B.
C. AD是A的平分线 D. ∠ABC是等边三角形
?
二. 填空题:
1. 如图,AB=DC,AD=BC,E、F是DB上两点且BE=DF,若∠AEB=100°,∠ADB=,则∠BCF= 。
2. 如图,若,,则 。
3. 如图在中,AB=AC,BE、CF是中线,则由 可得。
4. 如图AB=CD,AD=BC,O为BD中点过O点作直线与DA、BC延长线交于E、F,若,EO=10,则∠DBC= ,FO= 。
5. 如图,AB=AC,BD=DC,若,则 。
?
三. 解答题:
1. 如图已知BF=CE,BC=EF,AB=DE,求证:∠A=∠D。
2. 如图OA=OB,点C、D分别在OA、OB上,且OC=OD,AD、BC交于E,求证:OE平分∠AOB。
3. 已知AC、EF相交于O,且AO=CO,BO=DO,EO=OF,求证:。
4. 已知∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,求证:AB=ED。
?
?
答案
一.
1. B 2. B 3. D 4. A 5. C 6. C 7. D 8. B 9. D 10. D
?
二.
1. 70° 2. 27° 3. SAS 4. 60°;10 5. 28°
?
二.
1.
证明:连结FC,在与中, ∴ (SSS)
∴ ∠1=∠2、∠3=∠4(全等三角形对应角相等)
∴ ∠EFB=∠BCE 又 ∵ AB=ED ∴ AC=FD
在△FDB与△ACE中 ∴ (SAS)
∴ (全等三角形对应角相等)
2.
证明:在与中, ∴ (SAS)
∴ 、(全等三角形对应角相等) ∴ AC=DB
在与中 ∴ (AAS)
∴ AE=EB 在与中,
∴ (SSS) ∴ ∴ OE平分∠AOB
3.
证明:在与中, ∴ (SAS)
∴ AE=FC 同理
BE=FD ∴
在与中, ∴ (SAS)
4.
证明:延长BA、CE交于G,在中,
在中, ∵
∴ ∴
∴ ∴ 在与中
∴ (AAS)
∴ AB=ED(全等三角形对应边相等)
