人教版七上4.2 直线、射线、线段 第3课时 线段的性质及两点的距离 课件(共24张PPT)
文档属性
| 名称 | 人教版七上4.2 直线、射线、线段 第3课时 线段的性质及两点的距离 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 13:15:25 | ||
图片预览







文档简介
(共24张PPT)
人教版
七上
第四章
几何图形初步
4.2
直线、射线、线段
第3课时
线段的性质及两点的距离
教学重点:
“两点之间,线段最短”这一性质的应用及两点的距离有关运算.
教学难点:
“两点之间,线段最短”这一性质的应用及两点的距离有关运算.
情境引入
广场的绿化草地里本来没有路,部分人贪图一时的方便而走捷径,破坏草地而走出了一条路来,为什么这些人喜欢从草地上穿过而走捷径吗?
探究新知
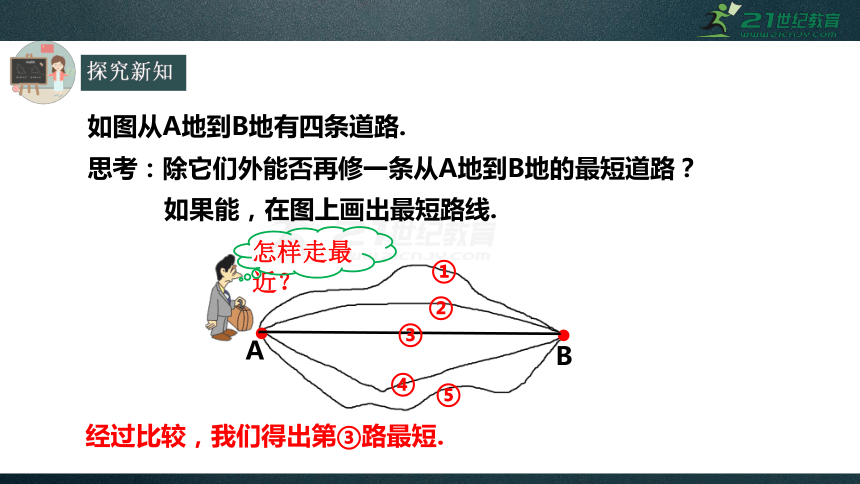
如图从A地到B地有四条道路.
●
●
A
B
怎样走最近?
思考:除它们外能否再修一条从A地到B地的最短道路?
如果能,在图上画出最短路线.
①
②
③
④
⑤
经过比较,我们得出第③路最短.
归纳
我们发现一个关于线段的基本事实(线段的性质):
线段的性质:
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
探究新知
你能举例说明“两点之间,线段最短”的实际应用吗?与同学们交流一下.
1.道路会尽可能修直一点.
2.人们为了走捷径,破坏草地而走出了一条路来.
练一练
1.如图,为抄近路践踏草坪是一种不文明的现象.请你用数学知识解释出现这一现象的原因
.
两点之间,线段最短
2.把甲、乙两地间一段弯曲的公路改为直路,可以缩短路程,其理由是(
).
A
两点之间,线段最短
B
两点确定一条直线
C
两点之间,直线最短
D
两点确定一条线段
A
例题讲解
例1
如图,平面上有A、B、C、D四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池,不考虑其他因素,请你画出确定蓄水池P的位置,使它与4个村庄的距离之和最小.
A
●
B
●
C
●
D
●
例题讲解
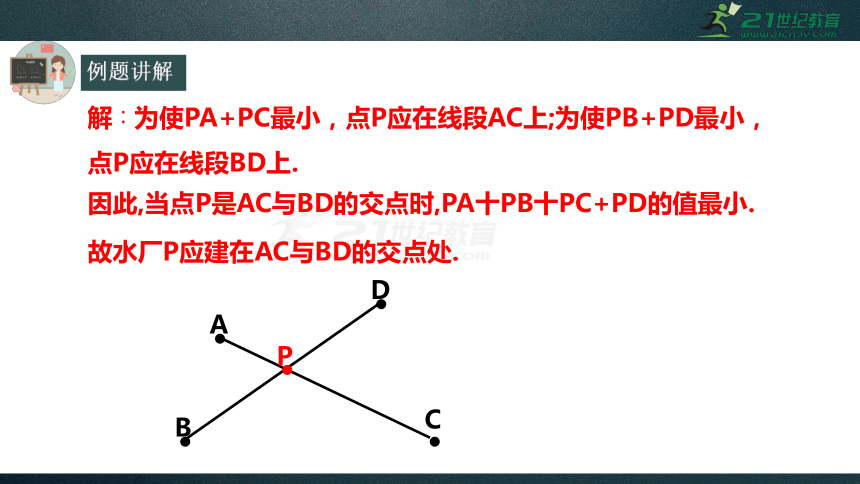
解∶为使PA+PC最小,点P应在线段AC上;为使PB+PD最小,点P应在线段BD上.
因此,当点P是AC与BD的交点时,PA十PB十PC+PD的值最小.
故水厂P应建在AC与BD的交点处.
A
●
B
●
C
●
D
●
P
●
练一练
如图,A、B是公路n两旁的两个村庄,若两村要在公路边上建立一个便民侯车亭,使它到A、B两村的距离和最小,试在n上标注出点P的位置,并说明理由.
A
●
B
●
P
●
n
解:连接AB交n于点P.
则P点为汽车站位置.
理由是:两点之间,线段最短.
探究新知
如图,在平面内
M、N两点之间的距离是(
).
M
●
N
●
A
B
C
D
C
连接两点间的线段的长度,叫做这两点的距离.
两点的距离:
练一练
关于两点之间的距离,下列说法正确的是( ).
A
连结两点的线段叫做两点间的距离.
B
两点间的连线的长度,叫做两点间的距离.
C
连结两点的直线的长度,叫做两点的距离.
D
连结两点的线段的长度,叫做两点间的距离.
D
例题讲解
例2
若A,B,C在同一条直线上,线段AB=10
cm,BC=2
cm,则A,C两点间的距离.
分析:题目中只说明了A、B、C三点在同一直线上,无法判定点C在线段AB上,还是在线段AB外(也就是在线段AB的延长线上).所以要分两种情况求线段AM的长.
例题讲解
AC=AB+BC=10+2=12(cm);
解:(1)点C在A,B之间时,
AC=AB-BC=10-2=8(cm).
所以A,C两点间的距离是12
cm或8
cm.
(2)当点C在A,B的延长线上时,
A
●
C
●
B
●
A
●
C
●
B
●
课堂练习
1.
下列现象,可用基本事实“两点之间,线段最短”来解释的是( ).
A
用两个钉子就可以把木条固定在墙上.
B
把弯曲的公路改直,就能缩短路程.
C
利用圆规可以比较两条线段的长短关系.
D
植树时,只要定出两棵树的位置,就能确定同一行.
B
课堂练习
2.
A,B,C是不在一条直线上的三个点,下列判断不正确的是( )
A
AB+AC>BC
B
BC+AC>AB
C
AB+BC>AC
D
AB+BC=AC
3.
若点B在线段AC上,AB=5,BC=3,则A,C两点间的距离是( )
A
8
B
2
C
4
D
无法确定
D
B
4.如图点C在线段AB上,点D是AC的中点,如果CD=3
cm,AB=10
cm,那么BC的长度是( )
A.3
cm
B.3.5
cm
C.4
cm
D.4.5
cm
课堂练习
A
●
C
●
B
●
D
●
C
课堂练习
5.
(1)把原来弯曲的河道改直,A,B
两地间的河道长度有什么
变化?
答:A,B
两地间的河道长度变短.
A
B
课堂练习
(2)公园修建了曲折迂回的桥,这与修一座直的桥相比,对游
人观赏湖面风光能起什么作用?
答:这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.
课堂练习
6.
已知线段AB=14cm,在直线AB上有一点C,且BC=4cm,M是线段AC的中点,求线段AM的长.
解:①当点C在线段AB上时,如图所示
因为M是AC的中点
所以AM=
AC
;
因为AC=AB-BC,AB=14cm,
BC=4cm
A
●
C
●
B
●
M
●
所以AM=
(AB-BC)
=
(14-4)=5cm
课堂练习
解:②当点C在线段AB延长线上时,如图所示
因为M是AC的中点
所以AM=
AC
;
因为AC=AB+BC,AB=14cm,
BC=4cm
A
●
C
●
B
●
M
●
所以AM=
(AB+BC)
=
(14+4)=9cm
所以线段AM的长为5cm或9cm.
课堂小结
1.线段的基本事实(线段的性质):
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
2.两点的距离:
课外作业
习题4.2
第130页第10、11题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
第四章
几何图形初步
4.2
直线、射线、线段
第3课时
线段的性质及两点的距离
教学重点:
“两点之间,线段最短”这一性质的应用及两点的距离有关运算.
教学难点:
“两点之间,线段最短”这一性质的应用及两点的距离有关运算.
情境引入
广场的绿化草地里本来没有路,部分人贪图一时的方便而走捷径,破坏草地而走出了一条路来,为什么这些人喜欢从草地上穿过而走捷径吗?
探究新知
如图从A地到B地有四条道路.
●
●
A
B
怎样走最近?
思考:除它们外能否再修一条从A地到B地的最短道路?
如果能,在图上画出最短路线.
①
②
③
④
⑤
经过比较,我们得出第③路最短.
归纳
我们发现一个关于线段的基本事实(线段的性质):
线段的性质:
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
探究新知
你能举例说明“两点之间,线段最短”的实际应用吗?与同学们交流一下.
1.道路会尽可能修直一点.
2.人们为了走捷径,破坏草地而走出了一条路来.
练一练
1.如图,为抄近路践踏草坪是一种不文明的现象.请你用数学知识解释出现这一现象的原因
.
两点之间,线段最短
2.把甲、乙两地间一段弯曲的公路改为直路,可以缩短路程,其理由是(
).
A
两点之间,线段最短
B
两点确定一条直线
C
两点之间,直线最短
D
两点确定一条线段
A
例题讲解
例1
如图,平面上有A、B、C、D四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池,不考虑其他因素,请你画出确定蓄水池P的位置,使它与4个村庄的距离之和最小.
A
●
B
●
C
●
D
●
例题讲解
解∶为使PA+PC最小,点P应在线段AC上;为使PB+PD最小,点P应在线段BD上.
因此,当点P是AC与BD的交点时,PA十PB十PC+PD的值最小.
故水厂P应建在AC与BD的交点处.
A
●
B
●
C
●
D
●
P
●
练一练
如图,A、B是公路n两旁的两个村庄,若两村要在公路边上建立一个便民侯车亭,使它到A、B两村的距离和最小,试在n上标注出点P的位置,并说明理由.
A
●
B
●
P
●
n
解:连接AB交n于点P.
则P点为汽车站位置.
理由是:两点之间,线段最短.
探究新知
如图,在平面内
M、N两点之间的距离是(
).
M
●
N
●
A
B
C
D
C
连接两点间的线段的长度,叫做这两点的距离.
两点的距离:
练一练
关于两点之间的距离,下列说法正确的是( ).
A
连结两点的线段叫做两点间的距离.
B
两点间的连线的长度,叫做两点间的距离.
C
连结两点的直线的长度,叫做两点的距离.
D
连结两点的线段的长度,叫做两点间的距离.
D
例题讲解
例2
若A,B,C在同一条直线上,线段AB=10
cm,BC=2
cm,则A,C两点间的距离.
分析:题目中只说明了A、B、C三点在同一直线上,无法判定点C在线段AB上,还是在线段AB外(也就是在线段AB的延长线上).所以要分两种情况求线段AM的长.
例题讲解
AC=AB+BC=10+2=12(cm);
解:(1)点C在A,B之间时,
AC=AB-BC=10-2=8(cm).
所以A,C两点间的距离是12
cm或8
cm.
(2)当点C在A,B的延长线上时,
A
●
C
●
B
●
A
●
C
●
B
●
课堂练习
1.
下列现象,可用基本事实“两点之间,线段最短”来解释的是( ).
A
用两个钉子就可以把木条固定在墙上.
B
把弯曲的公路改直,就能缩短路程.
C
利用圆规可以比较两条线段的长短关系.
D
植树时,只要定出两棵树的位置,就能确定同一行.
B
课堂练习
2.
A,B,C是不在一条直线上的三个点,下列判断不正确的是( )
A
AB+AC>BC
B
BC+AC>AB
C
AB+BC>AC
D
AB+BC=AC
3.
若点B在线段AC上,AB=5,BC=3,则A,C两点间的距离是( )
A
8
B
2
C
4
D
无法确定
D
B
4.如图点C在线段AB上,点D是AC的中点,如果CD=3
cm,AB=10
cm,那么BC的长度是( )
A.3
cm
B.3.5
cm
C.4
cm
D.4.5
cm
课堂练习
A
●
C
●
B
●
D
●
C
课堂练习
5.
(1)把原来弯曲的河道改直,A,B
两地间的河道长度有什么
变化?
答:A,B
两地间的河道长度变短.
A
B
课堂练习
(2)公园修建了曲折迂回的桥,这与修一座直的桥相比,对游
人观赏湖面风光能起什么作用?
答:这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.
课堂练习
6.
已知线段AB=14cm,在直线AB上有一点C,且BC=4cm,M是线段AC的中点,求线段AM的长.
解:①当点C在线段AB上时,如图所示
因为M是AC的中点
所以AM=
AC
;
因为AC=AB-BC,AB=14cm,
BC=4cm
A
●
C
●
B
●
M
●
所以AM=
(AB-BC)
=
(14-4)=5cm
课堂练习
解:②当点C在线段AB延长线上时,如图所示
因为M是AC的中点
所以AM=
AC
;
因为AC=AB+BC,AB=14cm,
BC=4cm
A
●
C
●
B
●
M
●
所以AM=
(AB+BC)
=
(14+4)=9cm
所以线段AM的长为5cm或9cm.
课堂小结
1.线段的基本事实(线段的性质):
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
2.两点的距离:
课外作业
习题4.2
第130页第10、11题
https://www.21cnjy.com/help/help_extract.php
