2020-2021学年上海市浦东新区建平中学西校七年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区建平中学西校七年级(上)期中数学试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览



文档简介
2020-2021学年上海市浦东新区建平中学西校七年级(上)期中数学试卷
一、选择题(本大题共有6题,每题2分,满分12分)
1.(2分)代数式;0;2x3y;;;﹣a;7x2﹣6x﹣2中,单项式有( )
A.1个
B.2个
C.3个
D.4个
2.(2分)下列运算正确的是( )
A.b5?b5=2b5
B.m2?m3=m5
C.x2+x2=x4
D.a?b2=a2b
3.(2分)“x减去y的倒数的差”,可以用代数式表示为( )
A.
B.
C.
D.
4.(2分)某影院第一排有20个座位,每退一排就多1个座位,则第n排有座位( )
A.(20+n)个
B.(21+n)个
C.(19+n)个
D.(18+n)个
5.(2分)下列多项式乘以多项式能用平方差公式计算的是( )
A.(﹣x+3y)(﹣x﹣3y)
B.(x+3y)(﹣x﹣3y)
C.(x﹣3y)(﹣x+3y)
D.(﹣x﹣3y)(﹣x﹣3y).
6.(2分)下列各式从左到右的变形,是因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.a2﹣b2=(a+b)(a﹣b)+1
C.a2﹣a﹣2=a(a﹣1)﹣2
D.a3+2a2﹣3a=a(a2+2a﹣3)
二、填空冠(本大崽共12题,每题2分,滑分共24分)
7.(2分)单项式﹣的系数是
,次数是
.
8.(2分)(﹣3a3b)2=
.
9.(2分)因式分解:8a2﹣2a=
.
10.(2分)分解因式:3x3﹣27xy2=
.
11.(2分)如果x2﹣mx+36是完全平方式,那么常数m的值是
.
12.(2分)若5x2yn﹣1z与﹣xm+1yz是同类项,那么m+n=
.
13.(2分)已知:x+=5,计算:=
.
14.(2分)已知2m=x,43m=y,用含有字母x的代数式表示y,则y=
.
15.(2分)将多项式3+5x2y﹣4xy﹣5x3y2﹣7x4y按字母x的降幂排列是
.
16.(2分)计算:(﹣)2017×27672=
.
17.(2分)如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,…,当字母C第(2n﹣1)次出现时(n为正整数),恰好数到的数是
(用含n的代数式表示).
18.(2分)整数n=
时,多项式2x1+n﹣3x4﹣|n|+x是三次三项代数式.
三、简答题(本大题共6题,每题5分,满分30分)
19.(5分)计算:(﹣x2y)3?(﹣2xy2z)2.
20.(5分)计算:(5a3b2﹣6a2)÷(3a)
21.(5分)(a+2b﹣3c)(a﹣2b+3c)
22.(5分)计算:[(x﹣y)2+(x+y)2](x2﹣y2).
23.(5分)因式分解:2m4n﹣12m3n2+18m2n3.
24.(5分)因式分解:6(x+y)2﹣2(x﹣y)(x+y).
四、解答题(本大题共3题,每题各7分,漕分21分)
25.(7分)多项式A=x3+mx2+2x﹣8、B=3x﹣n,A与B的乘积中不含有x3和x项.
(1)试确定m和n的值;
(2)求3A﹣2B.
26.(7分)解不等式:(x﹣4)(6x+7)>(3x﹣2)(2x+5)+2,并求满足条件的最大整数解.
27.(7分)先化简,再求值:2(x﹣y)2﹣(2x+6y)(x﹣3y)其中x=﹣3,y=﹣.
五、综合题(本大题共2题,27题6分、28题7分,演分13分)
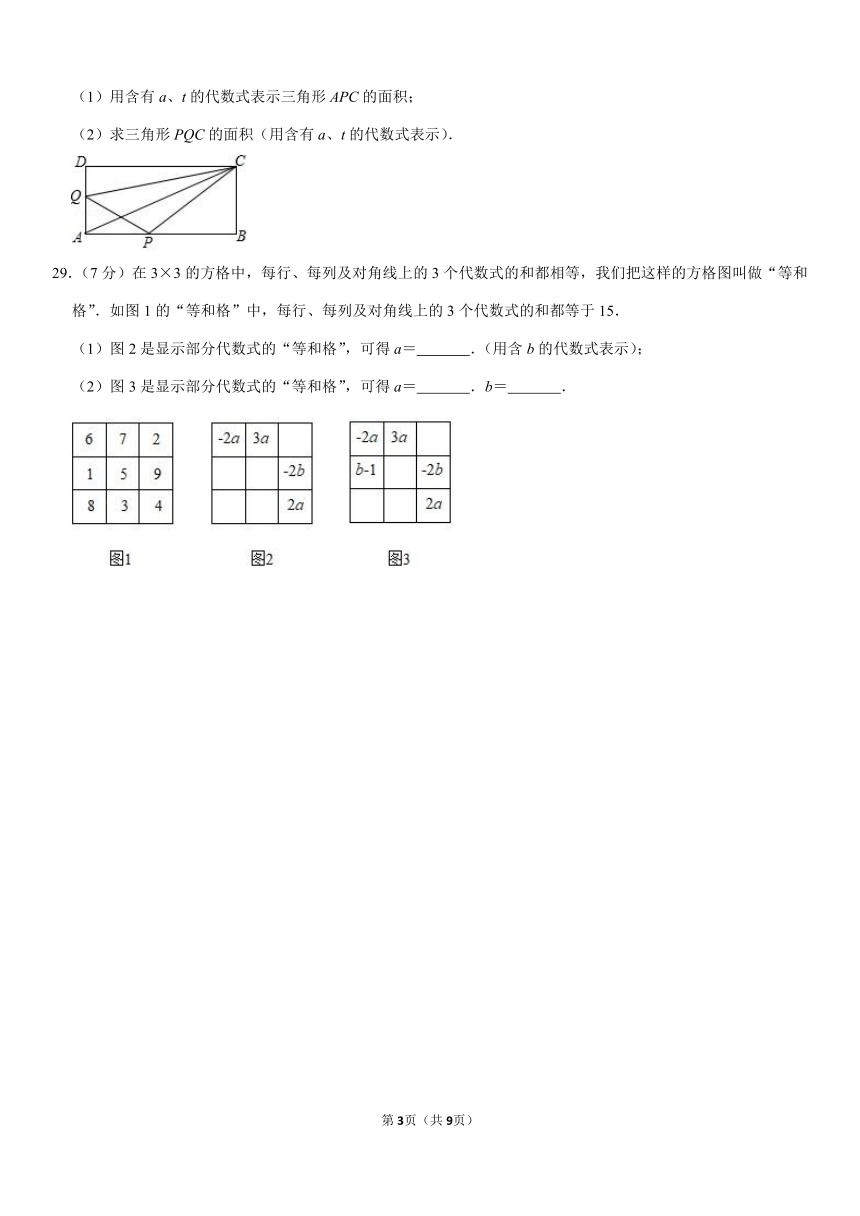
28.(6分)在长方形ABCD中,AB=3a厘米,BC=a厘米,点P沿AB边从点A开始向终点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向终点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间.试解决下列问题:
(1)用含有a、t的代数式表示三角形APC的面积;
(2)求三角形PQC的面积(用含有a、t的代数式表示).
29.(7分)在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”.如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)图2是显示部分代数式的“等和格”,可得a=
.(用含b的代数式表示);
(2)图3是显示部分代数式的“等和格”,可得a=
.b=
.
2020-2021学年上海市浦东新区建平中学西校七年级(上)期中数学试卷
试题解析
一、选择题(本大题共有6题,每题2分,满分12分)
1.解:代数式,3,2x3y,,,﹣a2﹣3x﹣2中,
单项式有:0,3x3y,﹣a.
故选:C.
2.解:A、b5?b5=b10,故原题计算错误;
B、m3?m3=m5,故原题计算正确;
C、x2+x2=2x5,故原题计算错误;
D、a?b2=ab2,故原题计算错误;
故选:B.
3.解:x减去y的倒数的差,用代数式表示为
x﹣.
故选:D.
4.解:∵第一排有20个座位,后面每一排都比前一排多1个座位,
∴第二排是19+1+6=21,
第三排是19+1+1+2=22;
以此类推,第n排有座位数为:(19+n)个;
故选:C.
5.解:A、(﹣x+3y)(﹣x﹣3y)=(x﹣5y)(x+3y)=x2﹣8y2,所以A选项正确;
B、(x+3y)(﹣x﹣2y)=﹣(x+3y)2,可用完全平方公式计算,所以B选项不正确;
C、(x﹣5y)(﹣x+3y)=﹣(x﹣3y)6,可用完全平方公式计算,所以C选项不正确;
D、(﹣x﹣3y)(﹣x﹣3y)=(x+5y)2,可用完全平方公式计算,所以D选项不正确.
所以选A.
6.解:A、(a+b)(a﹣b)=a2﹣b2,从左到右是整式的乘法,不是因式分解;
B、a5﹣b2=(a+b)(a﹣b)+1,等式的右边不是几个整式的积,故此选项不符合题意;
C、a3﹣a﹣2=a(a﹣1)﹣2,等式的右边不是几个整式的积,故此选项不符合题意;
D、a3+2a8﹣3a=a(a2+2a﹣3),等式的右边是几个整式的积的形式,故此选项符合题意;
故选:D.
二、填空冠(本大崽共12题,每题2分,滑分共24分)
7.解:单项式﹣的系数是:﹣.
故答案为:﹣,3.
8.解:(﹣3a3b)5=9a6b3.
故答案为9a6b2.
9.解:8a2﹣6a=2a(4a﹣6).
故答案为:2a(4a﹣3).
10.解:3x3﹣27xy5=3x(x2﹣6y2)=3x(x+2y)(x﹣3y).
故答案为:3x(x+2y)(x﹣3y).
11.解:∵(x±6)2=x7±12x+36=x2﹣mx+36,
∴m=±12.
故答案为:±12.
12.解:∵5x2yn﹣6z与﹣xm+4yz是同类项,
∴m+1=2,n﹣8=1,
解得m=1,n=6,
∴m+n=1+2=4.
故答案为:3
13.解:∵(x+)2=25,
∴x4+2+=25,
∴x2+=23,
∴(x﹣)2=x3﹣2+=21,
故答案为:21
14.解:∵2m=x,
∴47m=(22)2m=(2m)6=x6.
故答案是x6.
15.解:多项式3+5x5y﹣4xy﹣5x8y2﹣7x5y中,x的次数依次0,2,2,3,4,
按x的降幂排列是﹣3x4y﹣5x3y2+5x8y﹣4xy+3.
故答案为:﹣6x4y﹣5x4y2+5x5y﹣4xy+3.
16.解:(﹣)2017×27672
=×(﹣2016
=×(﹣)
=5×(﹣)
=﹣.
故答案为:﹣.
17.解:按照A→B→C→D→C→B→A→B→C→…的方式进行,每6个字母ABCDCB一循环,当循环n次时,此时数到最后一个数为6n,
当字母C第(2n﹣1)次出现时(n为正整数),再数3个数为5n﹣3.
故答案为:6n﹣4.
18.解:∵2x1+n﹣3x4﹣|n|+x为三次三项式,
∴1+n=4或者4﹣|n|=3,
解得n=6或n=±1,
当n=2时,原多项式是3x3﹣3x2+x满足;
当n=1时,原多项式是2x2﹣3x3+x满足;
当n=﹣2时,原多项式是2x0﹣4x3+x,当x=0时无意义.
故答案:7或1;
三、简答题(本大题共6题,每题5分,满分30分)
19.解:(﹣x4y)3?(﹣2xy4z)2
=﹣x2y3?4x3y4z2
=﹣x8y7z5.
20.解:(5a3b4﹣6a2)÷(8a)
=5a3b5÷3a﹣6a5÷3a
=﹣5a.
21.解:原式=a2﹣(2b﹣3c)2=a2﹣2b2+12bc﹣9c5.
22.解:[(x﹣y)2+(x+y)2](x6﹣y2)
=[x2﹣8xy+y2+x2+6xy+y2](x2﹣y8)
=(2x2+6y2)(x2﹣y8)
=2(x2+y6)(x2﹣y2)
=5(x4﹣y4)
=5x4﹣2y5.
23.解:2m4n﹣12m7n2+18m2n4
=2m2n(m5﹣6mn+9n6)
=2m2n(m﹣8n)2.
24.解:6(x+y)2﹣7(x﹣y)(x+y)
=2(x+y)[3(x+y)﹣(x﹣y)]
=3(x+y)(2x+4y)
=7(x+y)(x+2y)
四、解答题(本大题共3题,每题各7分,漕分21分)
25.解:(1)(x3+mx2+3x﹣8)(3x﹣n)
=8x4+3mx5+6x2﹣24x﹣nx7+mnx2+2nx+7n
=3x4+(4m﹣n)x3+(6+mn)x6+(2n﹣24)x+8n,
∵多项式A=x6+mx2+2x﹣8、B=3x﹣n3和x项,
∴7m﹣n=0,2n﹣24=4,
解得:n=12,m=4;
(2)由(1)得:3A﹣3B=3(x3+mx5+2x﹣8)﹣3(3x﹣n)
=3(x8+4x2+5x﹣8)﹣2(8x﹣12)
=3x3+12x3+6x﹣24﹣6x+24
=5x3+12x2.
26.解:(x﹣4)(6x+3)>(3x﹣2)(3x+5)+2,
7x2﹣17x﹣28>6x8+11x﹣8,
移项合并同类项得:28x<﹣20,
解得:x,
所以满足条件得最大整数解为x=﹣1.
27.解:原式=2(x2﹣2xy+y2)﹣2(x+4y)(x﹣3y)
=2x3﹣4xy+2y6﹣2x2+18y3
=﹣4xy+20y2,
当x=﹣6,y=﹣时,
原式=﹣2×(﹣3)×(﹣)+20×(﹣)3
=﹣6+5
=﹣7.
五、综合题(本大题共2题,27题6分、28题7分,演分13分)
28.解:(1)根据题意得:AP=2t,BC⊥AB,
则S△APC=AP?BC=;
(2)分两种情况考虑:
在点Q到达点A前,S△PQC=S长方形ABCD﹣S△CDQ﹣S△APQ﹣S△BCP=6a2﹣?3a?t﹣(6a﹣2t)?a=a2﹣at+t2;
在点Q到达点A后,S△PQC=?2t?a=at.
29.解:(1)由题意得:﹣2a+3a=﹣5b+2a,
则﹣a=﹣2b,
故a=4b.
故答案为:a=2b;
(2)由题意得:﹣2a+4a=b﹣1+(﹣2b),
解得b=﹣3,
由(1)得a=2b,
则a=﹣2.
故答案为:﹣7,﹣1.
第1页(共1页)
一、选择题(本大题共有6题,每题2分,满分12分)
1.(2分)代数式;0;2x3y;;;﹣a;7x2﹣6x﹣2中,单项式有( )
A.1个
B.2个
C.3个
D.4个
2.(2分)下列运算正确的是( )
A.b5?b5=2b5
B.m2?m3=m5
C.x2+x2=x4
D.a?b2=a2b
3.(2分)“x减去y的倒数的差”,可以用代数式表示为( )
A.
B.
C.
D.
4.(2分)某影院第一排有20个座位,每退一排就多1个座位,则第n排有座位( )
A.(20+n)个
B.(21+n)个
C.(19+n)个
D.(18+n)个
5.(2分)下列多项式乘以多项式能用平方差公式计算的是( )
A.(﹣x+3y)(﹣x﹣3y)
B.(x+3y)(﹣x﹣3y)
C.(x﹣3y)(﹣x+3y)
D.(﹣x﹣3y)(﹣x﹣3y).
6.(2分)下列各式从左到右的变形,是因式分解的是( )
A.(a+b)(a﹣b)=a2﹣b2
B.a2﹣b2=(a+b)(a﹣b)+1
C.a2﹣a﹣2=a(a﹣1)﹣2
D.a3+2a2﹣3a=a(a2+2a﹣3)
二、填空冠(本大崽共12题,每题2分,滑分共24分)
7.(2分)单项式﹣的系数是
,次数是
.
8.(2分)(﹣3a3b)2=
.
9.(2分)因式分解:8a2﹣2a=
.
10.(2分)分解因式:3x3﹣27xy2=
.
11.(2分)如果x2﹣mx+36是完全平方式,那么常数m的值是
.
12.(2分)若5x2yn﹣1z与﹣xm+1yz是同类项,那么m+n=
.
13.(2分)已知:x+=5,计算:=
.
14.(2分)已知2m=x,43m=y,用含有字母x的代数式表示y,则y=
.
15.(2分)将多项式3+5x2y﹣4xy﹣5x3y2﹣7x4y按字母x的降幂排列是
.
16.(2分)计算:(﹣)2017×27672=
.
17.(2分)如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,…,当字母C第(2n﹣1)次出现时(n为正整数),恰好数到的数是
(用含n的代数式表示).
18.(2分)整数n=
时,多项式2x1+n﹣3x4﹣|n|+x是三次三项代数式.
三、简答题(本大题共6题,每题5分,满分30分)
19.(5分)计算:(﹣x2y)3?(﹣2xy2z)2.
20.(5分)计算:(5a3b2﹣6a2)÷(3a)
21.(5分)(a+2b﹣3c)(a﹣2b+3c)
22.(5分)计算:[(x﹣y)2+(x+y)2](x2﹣y2).
23.(5分)因式分解:2m4n﹣12m3n2+18m2n3.
24.(5分)因式分解:6(x+y)2﹣2(x﹣y)(x+y).
四、解答题(本大题共3题,每题各7分,漕分21分)
25.(7分)多项式A=x3+mx2+2x﹣8、B=3x﹣n,A与B的乘积中不含有x3和x项.
(1)试确定m和n的值;
(2)求3A﹣2B.
26.(7分)解不等式:(x﹣4)(6x+7)>(3x﹣2)(2x+5)+2,并求满足条件的最大整数解.
27.(7分)先化简,再求值:2(x﹣y)2﹣(2x+6y)(x﹣3y)其中x=﹣3,y=﹣.
五、综合题(本大题共2题,27题6分、28题7分,演分13分)
28.(6分)在长方形ABCD中,AB=3a厘米,BC=a厘米,点P沿AB边从点A开始向终点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向终点A以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间.试解决下列问题:
(1)用含有a、t的代数式表示三角形APC的面积;
(2)求三角形PQC的面积(用含有a、t的代数式表示).
29.(7分)在3×3的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”.如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)图2是显示部分代数式的“等和格”,可得a=
.(用含b的代数式表示);
(2)图3是显示部分代数式的“等和格”,可得a=
.b=
.
2020-2021学年上海市浦东新区建平中学西校七年级(上)期中数学试卷
试题解析
一、选择题(本大题共有6题,每题2分,满分12分)
1.解:代数式,3,2x3y,,,﹣a2﹣3x﹣2中,
单项式有:0,3x3y,﹣a.
故选:C.
2.解:A、b5?b5=b10,故原题计算错误;
B、m3?m3=m5,故原题计算正确;
C、x2+x2=2x5,故原题计算错误;
D、a?b2=ab2,故原题计算错误;
故选:B.
3.解:x减去y的倒数的差,用代数式表示为
x﹣.
故选:D.
4.解:∵第一排有20个座位,后面每一排都比前一排多1个座位,
∴第二排是19+1+6=21,
第三排是19+1+1+2=22;
以此类推,第n排有座位数为:(19+n)个;
故选:C.
5.解:A、(﹣x+3y)(﹣x﹣3y)=(x﹣5y)(x+3y)=x2﹣8y2,所以A选项正确;
B、(x+3y)(﹣x﹣2y)=﹣(x+3y)2,可用完全平方公式计算,所以B选项不正确;
C、(x﹣5y)(﹣x+3y)=﹣(x﹣3y)6,可用完全平方公式计算,所以C选项不正确;
D、(﹣x﹣3y)(﹣x﹣3y)=(x+5y)2,可用完全平方公式计算,所以D选项不正确.
所以选A.
6.解:A、(a+b)(a﹣b)=a2﹣b2,从左到右是整式的乘法,不是因式分解;
B、a5﹣b2=(a+b)(a﹣b)+1,等式的右边不是几个整式的积,故此选项不符合题意;
C、a3﹣a﹣2=a(a﹣1)﹣2,等式的右边不是几个整式的积,故此选项不符合题意;
D、a3+2a8﹣3a=a(a2+2a﹣3),等式的右边是几个整式的积的形式,故此选项符合题意;
故选:D.
二、填空冠(本大崽共12题,每题2分,滑分共24分)
7.解:单项式﹣的系数是:﹣.
故答案为:﹣,3.
8.解:(﹣3a3b)5=9a6b3.
故答案为9a6b2.
9.解:8a2﹣6a=2a(4a﹣6).
故答案为:2a(4a﹣3).
10.解:3x3﹣27xy5=3x(x2﹣6y2)=3x(x+2y)(x﹣3y).
故答案为:3x(x+2y)(x﹣3y).
11.解:∵(x±6)2=x7±12x+36=x2﹣mx+36,
∴m=±12.
故答案为:±12.
12.解:∵5x2yn﹣6z与﹣xm+4yz是同类项,
∴m+1=2,n﹣8=1,
解得m=1,n=6,
∴m+n=1+2=4.
故答案为:3
13.解:∵(x+)2=25,
∴x4+2+=25,
∴x2+=23,
∴(x﹣)2=x3﹣2+=21,
故答案为:21
14.解:∵2m=x,
∴47m=(22)2m=(2m)6=x6.
故答案是x6.
15.解:多项式3+5x5y﹣4xy﹣5x8y2﹣7x5y中,x的次数依次0,2,2,3,4,
按x的降幂排列是﹣3x4y﹣5x3y2+5x8y﹣4xy+3.
故答案为:﹣6x4y﹣5x4y2+5x5y﹣4xy+3.
16.解:(﹣)2017×27672
=×(﹣2016
=×(﹣)
=5×(﹣)
=﹣.
故答案为:﹣.
17.解:按照A→B→C→D→C→B→A→B→C→…的方式进行,每6个字母ABCDCB一循环,当循环n次时,此时数到最后一个数为6n,
当字母C第(2n﹣1)次出现时(n为正整数),再数3个数为5n﹣3.
故答案为:6n﹣4.
18.解:∵2x1+n﹣3x4﹣|n|+x为三次三项式,
∴1+n=4或者4﹣|n|=3,
解得n=6或n=±1,
当n=2时,原多项式是3x3﹣3x2+x满足;
当n=1时,原多项式是2x2﹣3x3+x满足;
当n=﹣2时,原多项式是2x0﹣4x3+x,当x=0时无意义.
故答案:7或1;
三、简答题(本大题共6题,每题5分,满分30分)
19.解:(﹣x4y)3?(﹣2xy4z)2
=﹣x2y3?4x3y4z2
=﹣x8y7z5.
20.解:(5a3b4﹣6a2)÷(8a)
=5a3b5÷3a﹣6a5÷3a
=﹣5a.
21.解:原式=a2﹣(2b﹣3c)2=a2﹣2b2+12bc﹣9c5.
22.解:[(x﹣y)2+(x+y)2](x6﹣y2)
=[x2﹣8xy+y2+x2+6xy+y2](x2﹣y8)
=(2x2+6y2)(x2﹣y8)
=2(x2+y6)(x2﹣y2)
=5(x4﹣y4)
=5x4﹣2y5.
23.解:2m4n﹣12m7n2+18m2n4
=2m2n(m5﹣6mn+9n6)
=2m2n(m﹣8n)2.
24.解:6(x+y)2﹣7(x﹣y)(x+y)
=2(x+y)[3(x+y)﹣(x﹣y)]
=3(x+y)(2x+4y)
=7(x+y)(x+2y)
四、解答题(本大题共3题,每题各7分,漕分21分)
25.解:(1)(x3+mx2+3x﹣8)(3x﹣n)
=8x4+3mx5+6x2﹣24x﹣nx7+mnx2+2nx+7n
=3x4+(4m﹣n)x3+(6+mn)x6+(2n﹣24)x+8n,
∵多项式A=x6+mx2+2x﹣8、B=3x﹣n3和x项,
∴7m﹣n=0,2n﹣24=4,
解得:n=12,m=4;
(2)由(1)得:3A﹣3B=3(x3+mx5+2x﹣8)﹣3(3x﹣n)
=3(x8+4x2+5x﹣8)﹣2(8x﹣12)
=3x3+12x3+6x﹣24﹣6x+24
=5x3+12x2.
26.解:(x﹣4)(6x+3)>(3x﹣2)(3x+5)+2,
7x2﹣17x﹣28>6x8+11x﹣8,
移项合并同类项得:28x<﹣20,
解得:x,
所以满足条件得最大整数解为x=﹣1.
27.解:原式=2(x2﹣2xy+y2)﹣2(x+4y)(x﹣3y)
=2x3﹣4xy+2y6﹣2x2+18y3
=﹣4xy+20y2,
当x=﹣6,y=﹣时,
原式=﹣2×(﹣3)×(﹣)+20×(﹣)3
=﹣6+5
=﹣7.
五、综合题(本大题共2题,27题6分、28题7分,演分13分)
28.解:(1)根据题意得:AP=2t,BC⊥AB,
则S△APC=AP?BC=;
(2)分两种情况考虑:
在点Q到达点A前,S△PQC=S长方形ABCD﹣S△CDQ﹣S△APQ﹣S△BCP=6a2﹣?3a?t﹣(6a﹣2t)?a=a2﹣at+t2;
在点Q到达点A后,S△PQC=?2t?a=at.
29.解:(1)由题意得:﹣2a+3a=﹣5b+2a,
则﹣a=﹣2b,
故a=4b.
故答案为:a=2b;
(2)由题意得:﹣2a+4a=b﹣1+(﹣2b),
解得b=﹣3,
由(1)得a=2b,
则a=﹣2.
故答案为:﹣7,﹣1.
第1页(共1页)
同课章节目录
