29. 单元小结(共17张ppt)
图片预览





文档简介
(共17张PPT)
第29章
单元小结
人教版·九年级数学·下册
1.了解中心投影、平行投影的定义及有关概念,并能用其知识解释有关现象和解决一些实际问题.
2.理解、掌握视图和三视图的概念;善于从不同方向观察物体,能够将现实物体抽象成几何体,由几何体想象出它的三视图.
3.了解立体图形与平面图形的关系,培养学生的空间想象能力.
重点:投影与三视图.
难点:画三视图.
阅读课本P108页内容,熟记各知识要点.
过对本章的学习,你掌握了哪些知识?会解哪些类型的题?还有什么疑惑?
学生在讨论交流的基础之上,展示自己的疑惑,教师引导学生互助解决.
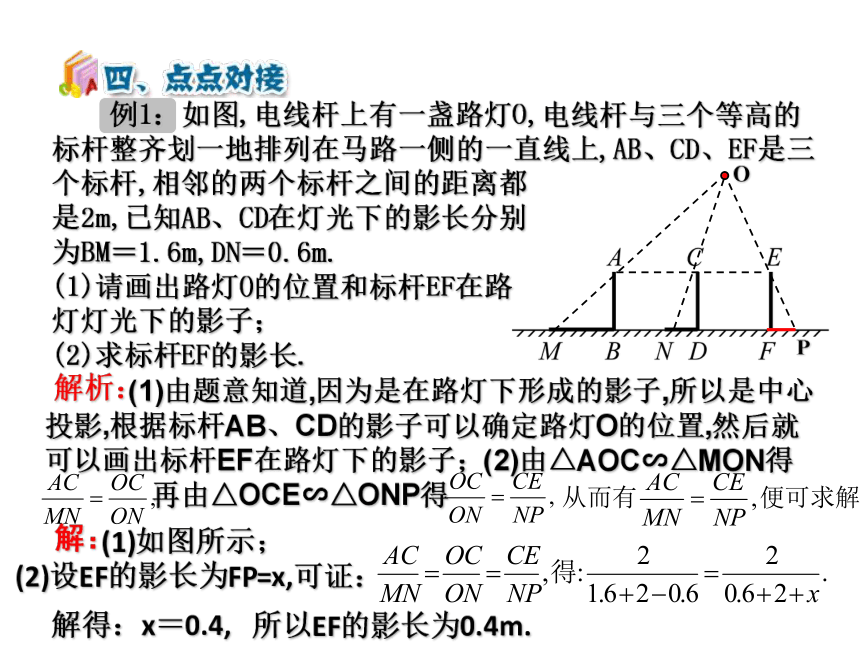
例1:如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路一侧的一直线上,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都
是2m,已知AB、CD在灯光下的影长分别
为BM=1.6m,DN=0.6m.
(1)请画出路灯O的位置和标杆EF在路
灯灯光下的影子;
(2)求标杆EF的影长.
解析:
(1)由题意知道,因为是在路灯下形成的影子,所以是中心投影,根据标杆AB、CD的影子可以确定路灯O的位置,然后就可以画出标杆EF在路灯下的影子;(2)由△AOC∽△MON得
解:
(1)如图所示;
再由△OCE∽△ONP得
O
P
(2)设EF的影长为FP=x,可证:
解得:x=0.4,
所以EF的影长为0.4m.
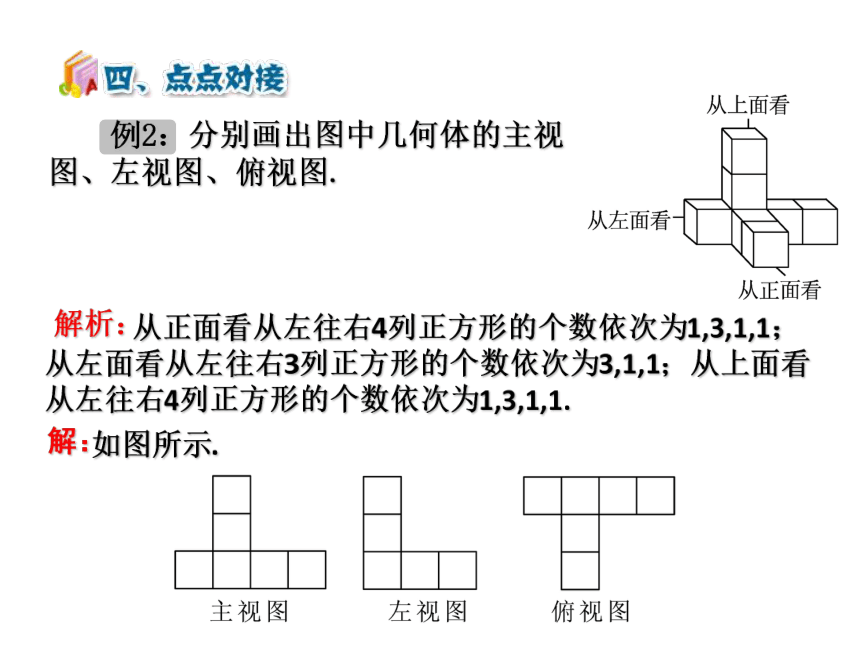
例2:分别画出图中几何体的主视
图、左视图、俯视图.
解析:
从正面看从左往右4列正方形的个数依次为1,3,1,1;从左面看从左往右3列正方形的个数依次为3,1,1;从上面看从左往右4列正方形的个数依次为1,3,1,1.
解:
如图所示.
例3:如图所示,三视图所对应的物体是(
)
根据三视图的判别法可知:这个几何体的下面是长方体、上面是圆柱体,并且圆柱体的直径和长方体的宽是相等的.
解析:
A.
答案:
A
例4:如图是一个物体的三视图,根据
设计图纸上标明的尺寸(单位:mm)计算
物体的表面积和体积.
由三视图可看出:物体是由上下两个半径不同的圆柱组成的,其立体图和展开图如图所示.
解析:
物体的立体图和表面展开图如图所
示,上面小圆柱的底面直径为4mm,高为
2mm,下面大圆柱的底面直径为8mm,高
为8mm.于是有物体体积:
解:
物体表面积:
例4:如图是一个物体的三视图,根据
设计图纸上标明的尺寸(单位:mm)计算
物体的表面积和体积.
由三视图可看出:物体是由上下两个半径不同的圆柱组成的,其立体图和展开图如图所示.
解析:
根据设计图纸中三视图及尺寸求
零件的表面积和体积,这是三视图在实际
生活中的主要应用,也是日常生产中经常
遇到的问题.解决这类问题的方法是首先
由三视图想象出几何体的形状,再画出其
表面展开图,然后根据图中尺寸利用相应
公式进行计算或解决最优化问题.
点评:
①②③④
远
3
B
D
解:
一天当中,物体在太阳光下的影子的方向依次是正西、北偏西、北偏东、正东.
④①③②
解:
修改如图:
本章要求理解平行投影、中心投影及正投影的概念,会判断物体的三视图,能根据三视图想象物体并会进行相关计算.
第29章
单元小结
人教版·九年级数学·下册
1.了解中心投影、平行投影的定义及有关概念,并能用其知识解释有关现象和解决一些实际问题.
2.理解、掌握视图和三视图的概念;善于从不同方向观察物体,能够将现实物体抽象成几何体,由几何体想象出它的三视图.
3.了解立体图形与平面图形的关系,培养学生的空间想象能力.
重点:投影与三视图.
难点:画三视图.
阅读课本P108页内容,熟记各知识要点.
过对本章的学习,你掌握了哪些知识?会解哪些类型的题?还有什么疑惑?
学生在讨论交流的基础之上,展示自己的疑惑,教师引导学生互助解决.
例1:如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路一侧的一直线上,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都
是2m,已知AB、CD在灯光下的影长分别
为BM=1.6m,DN=0.6m.
(1)请画出路灯O的位置和标杆EF在路
灯灯光下的影子;
(2)求标杆EF的影长.
解析:
(1)由题意知道,因为是在路灯下形成的影子,所以是中心投影,根据标杆AB、CD的影子可以确定路灯O的位置,然后就可以画出标杆EF在路灯下的影子;(2)由△AOC∽△MON得
解:
(1)如图所示;
再由△OCE∽△ONP得
O
P
(2)设EF的影长为FP=x,可证:
解得:x=0.4,
所以EF的影长为0.4m.
例2:分别画出图中几何体的主视
图、左视图、俯视图.
解析:
从正面看从左往右4列正方形的个数依次为1,3,1,1;从左面看从左往右3列正方形的个数依次为3,1,1;从上面看从左往右4列正方形的个数依次为1,3,1,1.
解:
如图所示.
例3:如图所示,三视图所对应的物体是(
)
根据三视图的判别法可知:这个几何体的下面是长方体、上面是圆柱体,并且圆柱体的直径和长方体的宽是相等的.
解析:
A.
答案:
A
例4:如图是一个物体的三视图,根据
设计图纸上标明的尺寸(单位:mm)计算
物体的表面积和体积.
由三视图可看出:物体是由上下两个半径不同的圆柱组成的,其立体图和展开图如图所示.
解析:
物体的立体图和表面展开图如图所
示,上面小圆柱的底面直径为4mm,高为
2mm,下面大圆柱的底面直径为8mm,高
为8mm.于是有物体体积:
解:
物体表面积:
例4:如图是一个物体的三视图,根据
设计图纸上标明的尺寸(单位:mm)计算
物体的表面积和体积.
由三视图可看出:物体是由上下两个半径不同的圆柱组成的,其立体图和展开图如图所示.
解析:
根据设计图纸中三视图及尺寸求
零件的表面积和体积,这是三视图在实际
生活中的主要应用,也是日常生产中经常
遇到的问题.解决这类问题的方法是首先
由三视图想象出几何体的形状,再画出其
表面展开图,然后根据图中尺寸利用相应
公式进行计算或解决最优化问题.
点评:
①②③④
远
3
B
D
解:
一天当中,物体在太阳光下的影子的方向依次是正西、北偏西、北偏东、正东.
④①③②
解:
修改如图:
本章要求理解平行投影、中心投影及正投影的概念,会判断物体的三视图,能根据三视图想象物体并会进行相关计算.
